基于需要的数学学习让学生眼中有“光”
2023-11-16胡玉兰
胡玉兰


【摘 要】基于需要的数学学习能让学生的眼中有“光”。在数学教学中,本就比较枯燥的数学知识如果再被机械化、模式化了,数学就会失去生命的色彩,学生学习起来也会更加乏味。而要让学生在数学课堂上乐于探索、发现与创造,让数学学习不再成为学生被动接受的过程,教师就必须从学生的情感需要出发,从教材关键点、学生易错处及教学生长点出发,直达知识本质,有效地激活学生的学习“兴趣码”,走近“最近發展区”,有针对性地进行课堂预设和实施教学。这样的数学学习才更有效,更能促进学生的发展。
【关键词】经验唤醒 激活内驱 自主探究 创新建构
低年级学生一般对数学学习比较感兴趣,上课积极参与,思维活跃,眼中有“光”。但是,随着年级的升高,数学课堂愈发沉闷,学生眼神暗淡,总是一副事不关己高高挂起的神态。究其原因,就是学生对数学学习缺乏兴趣。而造成这一结果的原因就是学生的学习兴趣被公式背诵、烦琐计算和重复练习消耗殆尽。
数学知识本身比较枯燥,如果再被教师前置化、模式化、机械化,数学就会失去生命的色彩,学生学习起来自然觉得厌倦乏味。而基于需要的数学学习则能激活学生的学习“兴趣码”,走近“最近发展区”,让学习不再成为学生被动接受的过程。因此,要让学生在数学课堂上乐于探索、发现与创造,教师就必须从学生的需要出发,从教材关键点、学生易错处及教学生长点出发,直达知识本质,从而有针对性地进行课堂预设和实施教学。这样的数学学习才更有效,更能促进学生的发展。
一、基于经验唤醒自动化的需要,进行有效预设
“凡事预则立,不预则废”,说明了事前预设的重要性。凡事多想一分,做足准备,则会事半功倍。备课也是如此,教师如果能在研读教材、研究学情的基础上把握学生的情感需要、已有知识储备与教学重难点,制订指向学生的学习目标,设计针对性强的问题,有效地进行积极的干预和促进,引导学生用喜欢的方式学习探究,就能大大地提升学生学习的主动参与度和学习目标的达成度,进而培养学生良好的学习心理品质。
(一)激活内驱,建立表象
只有学生真正喜欢的内容,才能激发他们的探究兴趣。因此,教师不妨在教学前先了解学生喜欢怎样的学习方式,从教材中发掘让学生感兴趣的内容,采取学生愿意接受的教学策略进行教学等,就能在最大程度上调动学生自主学习的积极性。“方程的认识”是苏教版数学五年级下册的内容,是学生认识代数相关知识的起点。教师应充分研读教材,合理创设良好的问题情境,通过丰富学生的感知,引导学生学会用数学的语言描述、用含有未知数的等式表达相关情境中的等量关系,同时启发学生通过观察分析、操作交流与归纳总结经历将现实生活问题抽象成等式与方程的过程,积累数学化活动经验,发现这类等式的共同特征,进而初步了解方程的含义。
(二)引导质疑,直达本质
教学中我们不难发现,学生一般对方程与等式的联系与区别及方程的本质特点的理解是不够深刻的,只是从表象上认识方程,而非真正实现意义的建构与理解。其实,在研读教材的基础上,我们可以明确学生理解的难点就是方程的本质特点:等式+未知数。因此,教师可直接通过引导质疑的方式发现学生的学习需要,并有机地融入相关的地方资源,有效渗透学生熟知的生活素材及部分方程史上的贡献等数学文化,丰富学生对方程的认知,引导他们经历从现实问题情境中抽象出方程的过程,从而理解方程的本质。例如:
(教师板书课题:方程)
师:关于方程,你最想知道什么?最困惑的是什么?
(学生提问,师小结并板书:A.是什么?B.为什么?(方程怎么来的?) C.干什么?)
师:这节课,我们就来解决这三个问题。同学们,不动笔墨不读书,请大家把书打开,自学课本2分钟,寻找答案。
(三)自主学习,建立概念
任何知识与技能的获得都是建立在学习者亲身体验、自主探索与有效建构的基础上的。只有经历了这个过程,学习者才能对所学内容有深刻理解,才能逐步内化,真正读懂。因此,引导学生依据自身经验,尝试主动探究发现、思考交流,就能促进他们认知水平、学习能力和思维品质的提升,从而深化其对所学知识的理解。
本节课中,教师开门见山地引导学生提出问题,然后通过让学生自主学习课本上的内容寻求解决问题的方法,满足了学生对新知的学习需要。基于学生的需要设计这个教学环节,就能准确地找到所有学生共同的困惑,也就是抓住了教学的核心内容,这样更能激发学生学习和探究的积极性。
(1)学生阅读课本有关内容后交流
(2)板书:等式+含有未知数=方程
(3)介绍方程的由来
课件逐步演示并播放相关录音:曾在700多年前,我国数学家李冶发明了“天元术”,他是第一个尝试用“天元”表示一些未知数的人。后来,数学家们受到启发,纷纷用各种不同的符号表示未知数,这在数学史上是一大进步。直至1637年,法国数学家笛卡尔最早提出可以用“x”表示未知数。这种表示方法简洁明了,被人们接受,后来逐渐成为人们表达的一种习惯。
二、基于知识理解结构化的需要,创设合理情境
基于学生的生活经验,教师从学生熟悉的天平平衡的直观情境出发,使学生感受“=”表示一种相等关系,经历用自然语言简单描述到数学语言准确表达的过程,明白“=”左右两边表示的是两个相等的量,从而直入方程的本质特点。在此基础上,通过引导学生进一步对一些问题情境进行数学化表达,对方程与等式进行辨析与比较,学生主动发现与建立概念间的联系与区别,丰富对数量之间关系的认识,实现了对方程这一概念的建立。
(一)情境吸引,直达本质
良好的学习情境创设可以更大程度地吸引学生的注意力,激发其浓厚的学习兴趣,促进他们的积极思维。
出示情境图1:
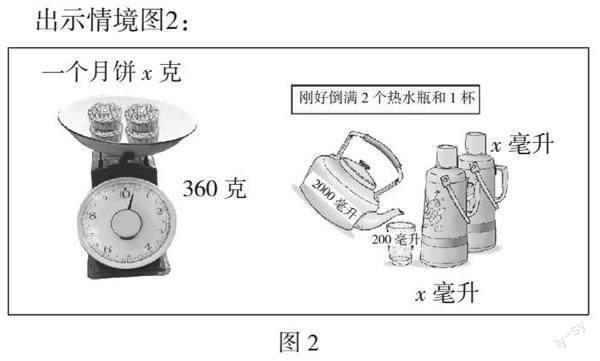
出示情境图2:
师:你能再用一个式子表示左右相等的关系吗?
(学生集体写于自备本上,指名板演)
(4x=360,200+2x=2000)
引导学生提问:A.我写的是方程吗?为什么? B.“=”是哪里来的?
交流强调:等式+含有未知数=方程
3.抓住事物本质,梳理归纳
师:刚才老师请大家用一个式子表示相等关系,为什么你们都写的是方程呢?你们明白什么是方程了吗?
生:方程就是表达相等关系的式子;方程就是有未知数的式子。
(二)建构联系,加深体悟
学者布莱基说过,组织得好的石头能成为建筑,组织得好的社会规则能成为宪法,组织得好的词汇能成为精彩的文章,甚至美丽的诗篇。数学知识具有很强的系统性,如果把所学的知识联系起来思考,在辨析和比较中发现本质区别,就能进一步深化对新知的理解。在这一环节教学中,教师引导学生进行观察、比较,从而深刻领悟了方程的本质特点。
(1)任意写出一些方程,能写完吗?(无数个)(指名板演,其余写于自备本上)
(2)圈出所有等式,圈出所有方程。
(3)观察所圈的结果,说说有什么发现。
x+5=10 1×1=1 4x=360
200+2x=2000 5+6=11 180+x=300
x+20=90+90 5+12=x 50+x﹤100
(4)小结:方程都是等式,等式不一定都是方程。
判断:下面式子哪些是方程,哪些不是方程?说说理由。
a+6 18+36=54 65+□=220
5y=75 m+30>900 80-B=4×15
三、基于思維发展系统化的需要,丰富学习体验
有应用价值的、贴近学生生活的知识比较容易被学生接受和记忆。因此,在数学教学中,教师需要充分建构数学与生活的联系,引导学生体会数学的应用价值,促使学生学会用数学的眼光主动发现世界,用数学的思维积极探索世界。
(一)立足生活,深化理解
让方程回归生活,可以把抽象的方程与生活情境建立联系,让学生换个思路理解方程。教师创设一定的语言情境,引导学生用生活问题解释对方程的理解或是在寻找一些方程的过程中,给方程增添更多的生命力,感受生活中处处有方程,方程就在我们身边,从而加深和丰富学生对方程意义的理解。
1.生活故事描述
课件显示:
65+□=220 5y=75 80-B=4×15
师:你能说说可以用这些方程分别表示生活中的哪些问题吗?
2.寻找身边的方程
教师请一名学生与自己同时站一起,然后问:“你能从中找到方程吗?”
(1)指名学生以此情境列出一些方程,教师则有目的地引导学生说出相应的等量关系。
(2)某同学身高a厘米,老师身高162厘米。两人相差21厘米。启发学生用不同的方程表示等量关系:a+21=162、162-a=21、162-21=a。
代数的基本特征就是用符号、字母表示数与运算的一种关系。教师以教材中的情境为导线,引导学生学会用数学语言表达情境中的等量关系,并逐步将其符号化,让学生明确等式与不等式都能用含有未知数的式子表达,为帮助学生对方程概念的有效建构奠定了基础,也使学生初步体会到含有未知数的式子可以描述等量关系的方程思想以及符号化思想的发展历程。
(二)回顾总结,经验提升
只有驻足,经历才能上升为经验,只有内化为自己的才是真正掌握的,只有学生真正需要的才是值得学习的。在本课学习结束环节,师生共同驻足,梳理知识。教师引用了笛卡尔的话:只要解决了方程问题,一切问题将迎刃而解!把一些现实问题都转化为一定的数学问题,再把数学问题转化为代数问题,最后用方程求解得到答案。现在看来,虽然这个观念并不十分准确合理,但很多现实问题的确可以通过方程来有效架起已知量和未知量之间的桥梁,从而顺利得到解决。
综上所述,这与学生的认知水平和在本节课内容的学习中所获得的初步体验是基本相符的,这样的数学学习能更好地调动学生的学习积极性,促使学生体悟所学知识与生活的紧密联系,从而逐步产生情感需要,学会自主建构对概念本质特征的认识。这样的数学课堂才是有生命力的,也更能让学生眼中有“光”!
