高速重载人字齿轮传动非线性动力学分析1)

莫 帅 曾彦钧 王 震 张 伟,

* (广西大学特色金属材料与组合结构全寿命安全国家重点实验室,南宁 530004)

† (广西大学机械工程学院,南宁 530004)

** (直升机传动技术国防科技重点实验室,南京 210016)

引言

人字齿轮可消除斜齿轮啮合过程中附加轴向载荷,增大重合度,使啮合更平稳,因此常用于武装直升机动力传输系统中.对人字齿轮系统非线性动力学特性进行分析,探究各因素对非线性行为影响,找出稳定运行区间,能为齿轮系统设计提供参考.

诸多学者深入探究不同因素对齿轮系统非线性行为影响[1-3].以上学者考虑时变啮合刚度、轴承游隙、齿侧间隙、间隙非线性函数和齿心偏差等因素影响,建立系统非线性动力学方程并求解.肖乾等[4]将齿间滑动及摩擦考虑在内,建立列车齿轮传动系统模型;莫帅等[5-6]将轮齿裂纹考虑在内,建立小模数变位齿轮故障动力学模型;袁冰等[7]将齿间累积误差和综合传递误差引入,建立人字齿轮非线性动力学模型;Mo 等[8-12]建立非正交面齿轮轴承系统模型,研究在不同激励频率下系统动力学响应及非线性全局行为演化过程,采用胞映射法研究非正交面齿轮轴承系统多自由度耦合振动模型动态行为演化过程.Chen 等[13]综合考虑摩擦、时变刚度对系统冲击影响,建立齿轮-转子-轴承系统多自由度非线性动力学模型;Miroslav 等[14]考虑时变啮合刚度与滚动轴承轴颈和外壳之间的非线性接触力,建立齿轮传动非线性动力学模型.诸多学者[15-17]提出动力学模型建立方式,对非线性动力学模型建立有推进作用.

王云等[18]建立了人字齿轮副平移-扭转振动分析模型,结合混合弹流润滑理论计算了混合弹流润滑摩擦因数,并探究其对系统动态特性影响;Yang等[19]提出一种由轴颈轴承支撑的人字齿轮转子系统耦合动力学模型,用时间位移图像、相平面图和分岔图从波度类型和波度幅值两方面研究人字齿轮转子系统非线性动力学行为;Xu 等[20]在摩擦动力学条件下,通过迭代数值方案提出一种新型HPGS耦合动力学模型,并对考虑齿面摩擦下该系统动力学特性进行研究,得出齿面摩擦与动态啮合力关系.Wang 等[21]等学者根据谐波平衡展开法和多尺度法分别推导单稳态能量收集器位移和电压频率响应函数,并从实验测量中确定单稳态系统参数,将其用于谐波平衡和多尺度方法理论解数值研究;Wang 等[22]和Moradi 等[23]分别建立铁路机车单自由度裂纹齿轮模型和直齿轮副非线性振动模型,采用多尺度方法对共振进行参数化研究,揭示不同因素对系统稳定性影响;诸多学者[24-30]采用不同研究方式,分别对考虑不同因素下系统非线性响应进行研究,使非线性动力学研究方法更加完善.

本文旨在研究高速重载人字齿轮传动系统非线性振动特性,综合考虑时变啮合刚度、传动误差、齿侧间隙和轴承间隙等因素,建立系统动力学模型,通过控制变量法,探究在不同齿侧间隙、啮合阻尼、啮合刚度及外部激励频率下系统非线性动力学响应,输出系统时间-位移图像、时间-速度图像、空间频谱图、空间相图、小波时频图及分岔图,通过观测图像曲线变化趋势判别系统是否稳定.

1 人字齿轮系统动力学模型

引入传递误差、时变啮合刚度和齿侧间隙等因素,考虑轴承滚动体与内外滚道之间游隙及轴承非线性振动,构建图1 所示人字齿轮系统多自由度耦合振动模型.

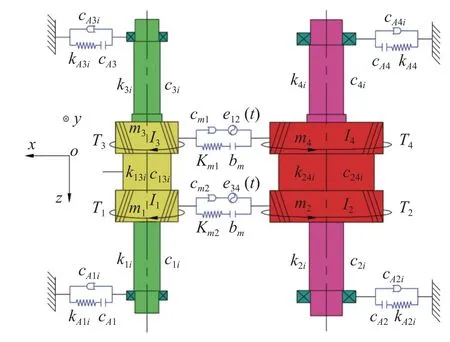
图1 人字齿轮系统多自由度耦合振动模型Fig.1 Multi-degree-of-freedom coupling vibration model of herringbone gear system

图中m1,m3,I1和I3分别为右、左两侧主动斜齿轮质量及右、左两侧主动斜齿轮转动惯量,m2,m4,I2和I4分别为右、左两侧从动斜齿轮质量及右、左两侧从动斜齿轮转动惯量;mA1和mA2分别为输入轴和输出轴右侧轴承质量,mA3和mA4分别为输入轴和输出轴左侧轴承质量;kA1i,kA2i,kA3i,kA4i,cA1i,cA2i,cA3i和cA4i(i=x,y)为各轴承内圈沿坐标轴x向和y向支撑刚度和支撑阻尼;k1i,k2i,k3i,k4i,c1i,c2i,c3i和c4i(i=x,y,z,θ)为齿轮与轴承连接轴段沿坐标轴x向、y向和z向支撑刚度、扭转刚度及相应阻尼;k13i,k24i,c13i和c24i(i=x,y,z,θ)为中间轴段沿坐标轴各向支撑刚度、扭转刚度及相应阻尼.

把轴承与旋转轴视作刚性连接,齿轮、一侧轴承与旋转轴质量集中在其质心,系统考虑24 个自由度

其中,xi,yi,zi,θi(i=1,2,3,4)为各斜齿轮沿坐标轴各向振动与扭转位移,xAj,yAj(j=1,2,3,4)为各轴承内圈沿坐标轴相应方向位移.

在本研究所用齿轮参数条件下,系统额定负载扭矩为200 N·m,最大工作转速超过5000 r/min,在高速重载工况下运行,其中,人字齿轮及轴承参数如表1 及表2 所示.

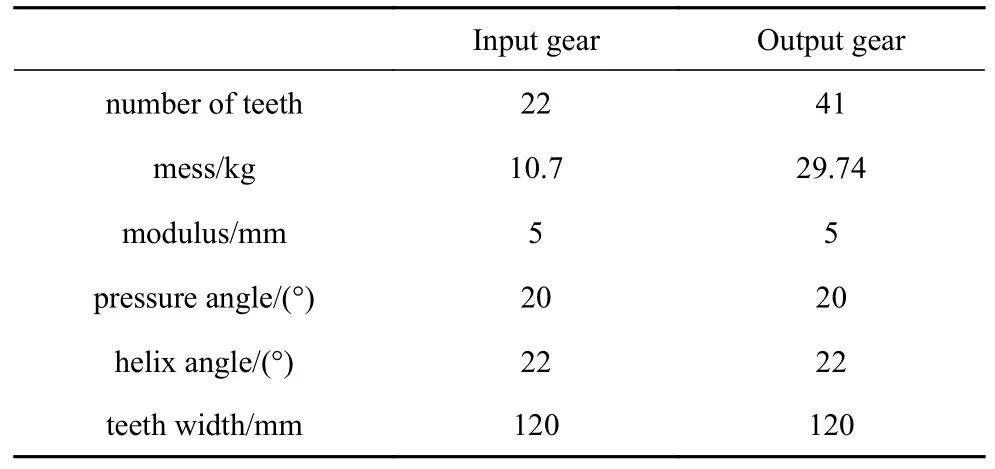
表1 人字齿轮参数Table 1 Parameters of the herringbone gears

表2 轴承参数Table 2 Bearing parameters

系统振动微分方程如下所示

为提升计算精度,以齿轮啮合线位移替换系统中齿轮扭转位移,将方程无量纲化,如下所示

式(1)和式(3)中,j取13,当i=1 时,p=3,k=1,v=1;当i=3 时,p=1,k=2,v=3.j取24,当i=2 时,p=1,k=1,v=2;当i=4 时,p=2,k=2,v=4;式(2)和式(4)中,当i=A1时,j=1;当i=A3时,j=3;当i=A2时,j=2;当i=A4时,j=4.

无量纲化方式如下所示

其中,τ表示无量纲时间,ωn表示固有频率,Km表示啮合刚度均值,fg为无量纲重力.

2 系统时变激励

2.1 时变啮合刚度及啮合力

定义右侧主动与从动斜齿轮啮合线为啮合线1,左侧主动与从动斜齿轮啮合线为啮合线2,αn和β为法面压力角和螺旋角,e为静态传递误差均值,ωm为斜齿轮副啮合频率,e(t)为静态传递误差,则右侧主动斜齿轮和右侧从动斜齿轮在啮合线1 上投影位移可由下式计算

基于此,啮合力计算方法如下

式中,Km(t)为该斜齿轮副时变啮合刚度;Cm为该斜齿轮副啮合阻尼,bm为齿侧间隙一半.

根据动力学模型中所建立三维坐标系,将啮合力分解至x,y,z方向,如下式所示

左侧斜齿轮副啮合力计算方式同理.

根据ISO standard 6336-1-2006 计算右侧斜齿轮副时变啮合刚度,如下式所示

式中,K(t)为斜齿啮合时变刚度,Km为平均啮合刚度,Ki为刚度变化幅值,ωm为啮合频率,其值等于输入轴转速频率乘以输入齿轮齿数,ϕ 为初始相位角,εα为端面重合系数,Kc为单对齿轮的啮合刚度.

左侧斜齿轮副时变啮合刚度可用相同方式计算.取相同参数,啮合线1 与啮合线2 时变啮合刚度曲线变化趋势相同,如图2 所示.

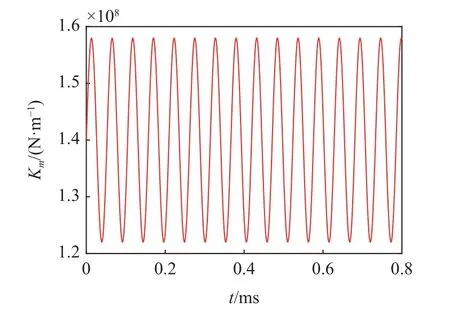
图2 时变啮合刚度曲线Fig.2 Time-varying meshing stiffness curve

2.2 时变轴承支撑力

轴承用于支撑旋转构件,其内部轴承力会对系统非线性响应产生影响.人字齿轮系统模型中,轴承载荷计算方式如下所示.

以ωbi和ωbo分别为轴承内、外圈绕旋转轴轴线转动角速度,由于外圈固定于轴承座,故ωbo=0.滚动体与轴承内、外圈接触点处线速度vbi和vbo,滚动体个数为Zb,轴承内、外圈半径分别为rbi和rbo,滚动体公转角速度ωbn及位置角θi(t)计算方式如下所示

轴承未因受力发生形变时,内、外圈曲率中心分别为Obi和Obo,曲率半径分别为rbi和rbo,滚动体与内、外圈初始接触角均为γi;轴承受力变形后,内、外圈曲率中心变为,接触角变为.因轴承外圈固定于轴承座,故受力时其曲率中心位置不变,轴承内圈曲率中心由Obi变化到.以l′为外圈曲率中心中心距,δ为滚动体变形,c为轴承径向游隙,为滚动体变形后与轴承内圈接触角,上述各项参数计算公式为

式中,x和y分别为轴承内圈沿坐标轴相应方向振动位移.

引入Heaviside 函数,以H(δ)表示,忽略滚动体及保持架惯性,Frb为滚动体径向受力,Kb为滚动体与滚道接触刚度,轴承内圈在坐标系各方向受力由下式计算

3 人字齿轮系统非线性动力学响应

选取额定输入转矩为150 N·m,探究改变不同系统参数时,系统动力学响应变化趋势.考虑到工程实际情况,在模型建立过程中,左、右斜齿轮副动态啮合误差激励波动幅值不同,啮合线1 和啮合线2 动力学响应曲线变化趋势存在差异.

3.1 不同转矩下系统响应

本部分探究输入转速为6000 r/min 时,人字齿轮传动系统在不同输入转矩下非线性响应.为更直观反映振动曲线数值,将啮合线1 和啮合线2 无量纲时间-位移曲线各点数值乘以bm,无量纲时间-速度曲线各点数值乘以ωnbm,绘制不同阻尼系数下系统响应,如图3所示.通过分析图3(a)和图3(b)可以看出,改变Tin值将改变振动位移曲轨迹变化趋势.图3(c)和图3(d)表明系统运动速度随时间变化关系,结合空间相图及庞加莱映射点可知,当Tin缓慢增加时,系统运动从稳定单周期运动逐渐变为双周期运动、多周期运动和混沌运动,且振幅逐渐增大,在此过程中,啮合线1 振动速度峰值为5.2 μm/s,啮合线2 振动速度峰值分别为0.27 μm/s,0.33 μm/s,4.5 μm/s 和5.3 μm/s.

图3 不同转矩下系统响应Fig.3 System response under different torque

3.2 不同啮合阻尼下系统响应

本部分探究输入转速为6000 r/min、输入转矩为150 N·m 时,人字齿轮传动系统在不同啮合阻尼系数下非线性响应.为更直观反映振动曲线数值,将啮合线1 和啮合线2 无量纲时间-位移曲线各点数值乘以bm,无量纲时间-速度曲线各点数值乘以ωnbm,绘制不同阻尼系数下系统响应,如图4 所示.通过分析图4(a)和图4(b)可以看出,改变ξm值将改变振动位移曲轨迹变化趋势.图4(c)和图4(d)表明系统运动速度随时间变化关系,结合空间相图及庞加莱映射点可知,当ξm缓慢增加时,系统运动从稳定单周期运动逐渐变为双周期运动和多周期运动,且振幅逐渐增大.

图4 不同阻尼系数下系统响应Fig.4 System response under different damping coefficients

3.3 不同齿侧间隙下系统响应

保持系统其他参数不变,改变bm值,分别观察啮合线1 和啮合线2 非线性位移.为更直观反映振动曲线数值,将啮合线1 和啮合线2 无量纲时间-位移曲线各点数值乘以bm,无量纲时间-速度曲线各点数值乘以ωnbm,绘制不同阻尼系数下系统响应,如图5 所示.从图5(a)和图5(b)可以看出,改变bm值将改变振动位移曲线的轨迹趋势.结合空间相图及庞加莱映射点可知,在不同bm值下,啮合线1 和啮合线2 运动状态总体变化趋势相同,当bm缓慢增大时,啮合线振动位移从稳定单周期运动逐渐变为双周期运动以及多周期运动,波动幅度逐渐增大.当齿侧间隙从1 μm 变化至4 μm 时,啮合线1 稳定单周期振动速度峰值为0.23 μm/s,混沌运动及多周期运动振动速度峰值为0.25 μm/s 和0.53 μm/s,啮合线2 稳定单周期振动速度峰值为2.5 μm/s.

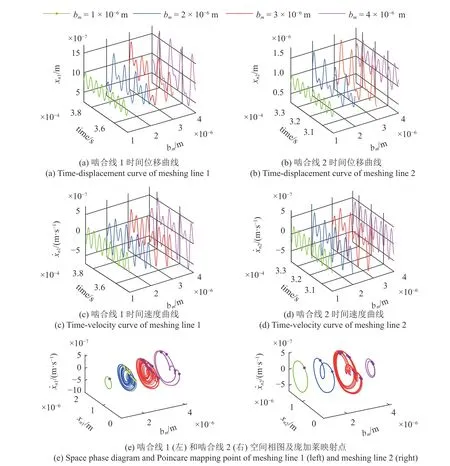
图5 不同齿侧间隙下系统响应Fig.5 System response under different backlashes

3.4 不同啮合刚度下系统响应

本部分探究在不同啮合刚度下系统非线性响应.为更直观反映振动曲线数值,将啮合线1 和啮合线2 无量纲时间-位移曲线各点数值乘以bm,无量纲时间-速度曲线各点数值乘以ωnbm,绘制不同阻尼系数下系统响应,如图6 所示.通过分析图6(a)和图6(b)可以看出,改变Km值将改变振动位移曲线的轨迹趋势.空间相图及庞加莱映射点表示,当Km缓慢增加时,庞加莱映射点集由散乱无序点变化为相轨迹线上两点,最终变化为相轨迹线上一点,表明啮合线上投影振动位移起初为混沌运动状态,随后逐渐变为倍周期运动状态,最后当啮合刚度突破一定阈值时,系统趋于稳定,做单周期运动.如图6(c)和图6(d)所示,在稳定运动状态下,啮合线1 稳定单周期振动速度峰值为0.43 μm/s,混沌运动及多周期运动振动速度峰值为0.8 μm/s 和0.33 μm/s,啮合线2 稳定单周期振动速度的峰值为0.45 μm/s.

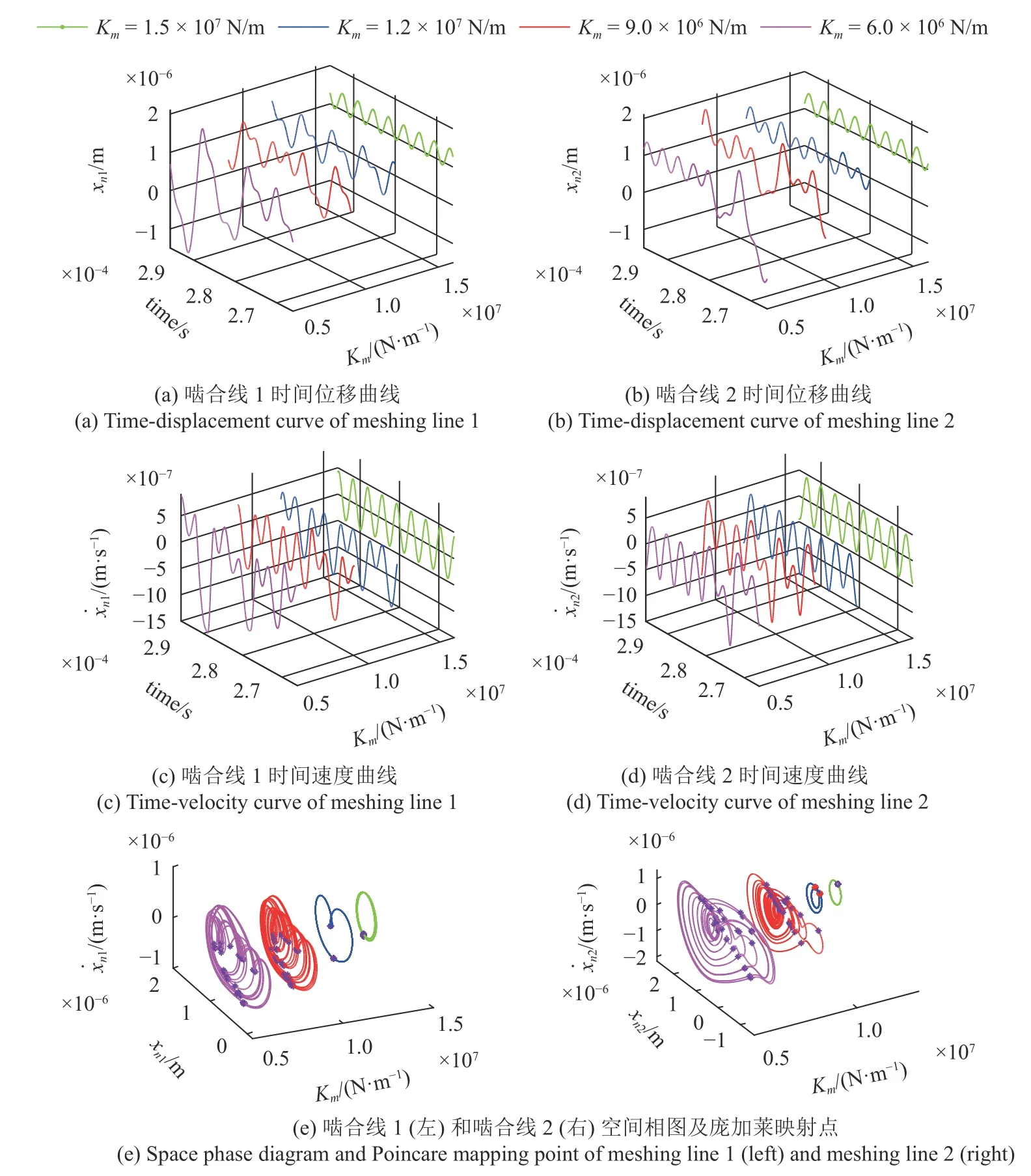
图6 不同啮合刚度下系统响应Fig.6 System response under different meshing stiffness

3.5 不同外部激励频率下系统响应

改变外激励频率,当输入转速逐渐增大至10 000 r/min 时,啮合线1 运动空间频谱如图7(a)所示.由图可知,当激励频率约为0.6 时,振动频率呈现单一峰值状态,表明系统处于稳定单周期运动状态.当激励频率约为1 时,振动频率出现两个峰值,幅值分别为0.3 和0.6,表明系统处于倍周期或多周期运动状态.同时,当激励频率约为1.25 和1.68 时,出现较多混沌频率,表明系统处于混沌运动状态.此外,图7(b)为空间状态下相平面图和庞加莱截面图,系统运动状态转变过程为: 从稳定单周期运动状态逐渐走向倍周期分岔运动状态和混沌运动状态,最终重新回到稳定周期运动状态.

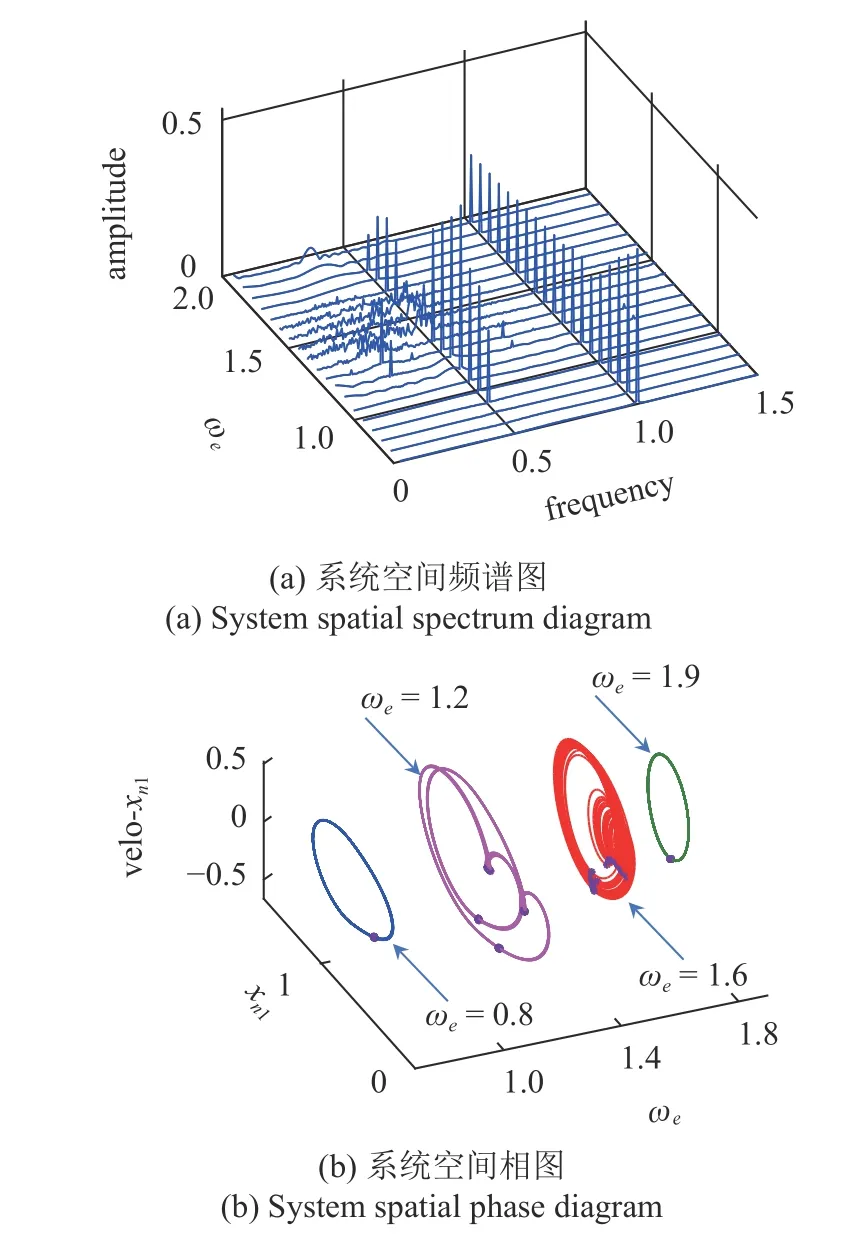
图7 啮合线1 空间频谱图及空间相图Fig.7 Spatial spectrum and spatial phase diagram of meshing line 1

通过小波变换方法分析啮合线上振动位移,如图8 所示.当ωe=0.7 时,啮合线上振动位移主要由0.1ωe组成,幅值约为0.28.当ωe=1 时,啮合线位移主振频率为0.8ωe和分量1.6ωe,系统处于倍周期运动状态.当ωe=1.55 时,除频率为0.25ωe外,还出现较多混沌频率,幅值集中在0.05 左右,此时系统在做混沌运动.当ωe=2.2 时,啮合位移主要由0.35ωe组成.幅值约为0.12,对应系统稳定单周期运动状态.

图8 啮合线1 小波变换时频图Fig.8 Meshing line 1 time-frequency diagram of wavelet transform

为进一步研究外部激励频率对系统动态特性影响,表征系统混沌运动状态,判别系统运动,绘制分岔参数为ωe时系统分岔图与李雅普诺夫指数图,如图9 所示.图中的数据表明,当ωe<0.7 时,最大李雅普诺夫指数小于0,系统振动位移变化周期与啮合周期一致,运动状态为稳定单周期运动;当ωe在0.7～1.2 之间时,系统振动位移变化周期为啮合周期2 倍,系统做倍周期运动;当ωe在1.2～1.3 之间时,系统振动位移变化周期为啮合周期4 倍,系统处于周期4 运动状态;当ωe在1.3～1.72 之间时,最大李雅普诺夫指数大于0,系统振动位移变化不再具有周期性,表明系统处于混沌运动状态;当ωe在1.72～1.88 之间时,系统振动位移变化周期为啮合周期二倍,系统做倍周期运动.当ωe>1.88 时,最大李雅普诺夫指数降到0 线以下,此时系统所处运动状态为稳定单周期运动.

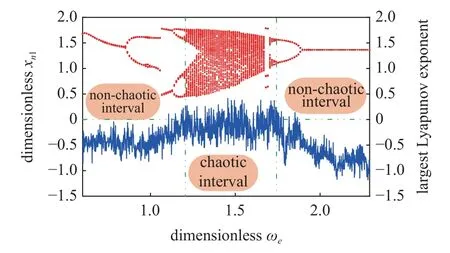
图9 啮合线1 系统位移分岔图及最大李雅普诺夫指数图Fig.9 Displacement bifurcation diagram and maximum Lyapunov exponent diagram of meshing line 1

改变外激励频率,当输入转速逐渐增大至10 000 r/min 时,啮合线2 运动空间频谱如图10(a)所示.由图可知,当激励频率小于0.7 时,频谱图上只出现单个主共振峰,振动幅值最大值为0.7,表明系统在做稳定单周期运动;当无量纲激励频率约为1.21 和1.75 时,系统振动频率出现多值现象,表明系统处于混沌运动状态.此外,图10(b)为空间相平面图和庞加莱截面图.图中信息表示,当无量纲激励频率ωe从0 开始增大至2 时,系统运动状态由稳定单周期运动状态过渡至多周期运动状态,随后陷入混沌运动状态,在经历倍周期运动状态后,最终转变回单周期运动状态,此时系统又趋于稳定.

图10 啮合线2 空间频谱图及空间相图Fig.10 Spatial spectrum and spatial phase diagram of meshing line 2

通过小波变换方法分析齿轮传动系统啮合线1 上振动位移变化趋势,如图11 所示.当ωe=0.6 时,坐标轴各向投影至啮合线上振动位移主要由0.1ωe组成,幅值约为0.27,表明系统稳定.当ωe=1.45 时,除频率为0.23ωe外,还出现较多混沌频率,幅值集中在0.1 左右.当ωe=2.1 时,啮合位移主要由0.35ωe组成,幅值约为0.12,对应系统稳定单周期运动状态.

图11 啮合线2 小波变换时频图Fig.11 Meshing line 2 time-frequency diagram of wavelet transform

图11 啮合线2 小波变换时频图 (续)Fig.11 Meshing line 2 time-frequency diagram of wavelet transform(continued)

为进一步研究外部激励频率对系统动态特性影响,表征系统混沌运动状态,判别系统运动,绘制分岔参数为ωe时系统分岔图及李雅普诺夫指数图,如图12 所示.图中的数据表明,当ωe<0.63 时,系统进行稳定单周期运动;当ωe在0.63～1.13 之间时,最大李雅普诺夫指数小于0,系统做倍周期运动;当ωe在1.13～1.25 之间时,系统处于周期4 运动状态;当ωe在1.25～1.75 之间时,系统处于混沌运动状态,此时,最大李雅普诺夫指数上升,突破0 线;当ωe在1.75～1.9 之间时,系统做倍周期运动.当ωe>1.9 时,最大李雅普诺夫指数降至负值,表明系统已经脱离混沌运动,进入稳定单周期运动.

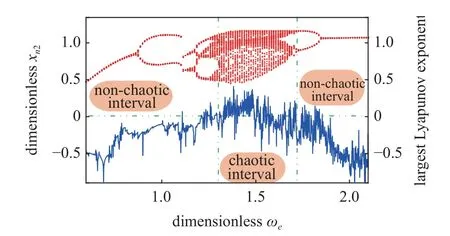
图12 啮合线2 系统位移分岔图及最大李雅普诺夫指数图Fig.12 Displacement bifurcation diagram and maximum Lyapunov exponent diagram of meshing line 2

4 结论

通过对高速重载人字轮非线性动力学分析得到如下结论.

(1)引入轴承游隙、齿侧间隙和动态啮合误差激励等因素,建立人字齿轮系统非线性动力学模型,通过控制变量法分析齿侧间隙对系统非线性特性影响,结果表明,当齿侧间隙取值范围为1×10-6～4×10-6m 时,若增大齿侧间隙,则系统周期运动稳定性降低.

(2)系统其他参数选定为初始参数,在150～300 N·m 范围内逐渐增大输入转矩以及在区间(0.15,0.3)内逐渐减小啮合阻尼比时,系统非线性振动由单周期演变为多周期和混沌,为使系统运动处于单周期运动状态,系统输入转矩不宜过高,啮合阻尼比不宜过低.

(3)通过控制变量法探究啮合刚度及激励频率对系统影响.在1.5×108～6×108N/m 范围内逐渐增大啮合刚度时,系统运动状态由混沌状态经历多周期运动状态后,最终变为稳定单周期运动状态.逐渐增大激励频率时,系统将经历周期、准周期、混沌及其他运动状态.为保证系统稳定运行,啮合刚度不宜过小,激励频率不应大于3250 Hz.