基于非线性耦合本构关系模型的尖化前缘气动加热影响研究1)

杨俊沅 李旭东 曾舒华 赵文文,2) 张 赋 陈伟芳

* (浙江大学航空航天学院,杭州 310027)

† (北京航天长征飞行器研究所,北京 100076)

引言

由于临近空间高超声速飞行器有着更快的飞行速度和高空机动能力,逐渐成为了世界各航空航天大国追逐的热点.对高超声速飞行器而言,升阻比越高,机动性越好[1].由于尖化前缘这一构型能够为飞行器提供更大的升阻比,高超声速飞行器的设计普遍选择尖前缘外形.然而,相比于钝头设计,高超声速来流在飞行器的尖化前缘处会产生更剧烈的气动加热现象,引发诸如气动热载荷大、热防护难等难题,给快速准确的热环境预示提出了更高的要求和挑战.尖化前缘热环境的准确刻画是尖化前缘热防护研究的前提[2].黄飞等[3]分别采用纳维-斯托克斯(Navier-Stokes,NS)方程和蒙特卡洛直接数值模拟(direct simulation Monte Carlo,DSMC)方法计算不同努森数条件下尖前缘气动特性,发现驻点热流密度受局部稀薄效应影响较大.姜贵庆等[4]发现尖化前缘表面热流密度在离驻点2～3 个分子自由程长度时下降至驻点热流密度的1/3,而表面温度此处仅下降至驻点温度的90%.表明尖化前缘的局部稀薄效应对驻点热流密度的精确预示产生了较大影响.工程问题中,连续流条件下驻点热流密度的工程快速预测通常可采用Fay-Riddell 公式[5],热流密度和前缘半径的关系可以表示为

式中,qs为尖化前缘的驻点热流密度,RN表示飞行器的前缘半径.当前缘半径过小时,驻点处易出现显著的局部稀薄气体效应,基于连续介质假设和层流边界层假设的Fay-Riddell 公式也会失效.理论上前缘半径趋近于0 时,驻点热流密度将趋近于无穷大,但实际上热流密度会趋近于自由分子流的极限[6].

在含局部稀薄效应的连续-稀薄耦合流动区域,NS 方程线性本构模型不足以准确描述稀薄非平衡和多尺度非线性的流动机理.高超声速飞行器的飞行环境介于稠密大气层和稀薄大气层之间,飞行环境不再单一,在尖前缘可能出现显著的局部稀薄气体效应,叠加滑移边界条件的NS 方程结果仍需通过实验数据或其他多尺度高精度计算模型进行校准[7].近年来,针对连续-稀薄跨流域流动现象的描述,Myong 等[8]在广义流体动力学方程基础上发展了非线性耦合本构关系(nonlinear coupled constitutive relations,NCCR)模型,并通过经典非平衡流动问题验证了NCCR 模型准确描述高速多尺度和稀薄非平衡流动现象的能力[9-11].随后,NCCR 模型得到了国内外众多学者的深入研究和理论验证[12-14],在计算框架[15]、求解算法[16-18]、边界条件[19-20]、热化学非平衡流动[21-23]、非结构网格求解[24-25]等方面进展显著.然而,NCCR 模型在高速连续/稀薄流实验验证方面的研究工作寥寥[26],并且缺少专门针对局部稀薄条件下的尖化前缘气动加热机理的影响研究.

本文首先通过圆柱绕流算例验证NCCR 模型的非平衡多尺度模拟能力;再通过对比等效高度33 km和60 km 条件下NCCR 模型计算的流场温度和壁面热流分布与实验值的偏差,检验NCCR 模型在尖化前缘构型中准确描述局部稀薄非平衡流动和物面气动热的性能.

1 非线性耦合本构关系模型

非线性耦合本构关系模型是Eu 在广义流体动力学方程的基础上对高阶非守恒量的时间项和对流项进行简化处理得到的[27-28].守恒量和非守恒量的方程可写为

式中,ρ,u,p,E,T分别为密度、速度、压力、能量和温度,Π,∆,Q,I,cp分别表示剪切应力张量、附加体积应力、热流、单位矩阵和气体的定压比热;η,ηb,λ为剪切黏性系数、体积黏性系数和热传导系数;是气体的比热比,q(κ)是非线性耗散项,非线性耗散项q(κ)的引入不仅增强了方程组的非线性度,同时使非守恒变量都耦合在一起

经过Eu 的高阶矩封闭以及Eu 和Myong 绝热假设简化[8],可以得到非线性耦合本构关系模型表达式为

为方便比较,NS 方程线性本构模型也在这给出

通过对比可以看出,NCCR 模型具有更强的非线性,从而在非平衡流动问题描述中可能具备更高的模拟精度和准确性.

2 算例验证

为验证非线性耦合本构关系模型求解连续-稀薄跨流域流动问题,本文选取了以压缩流动为主的高超声速圆柱绕流算例对NCCR 模型理论体系进行验证.圆柱算例半径为6 inch (1 inch=2.54 cm),计算域网格采用结构网格,壁面和径向方向网格数目分别为100 和100.气体黏性使用逆幂律分子模型求解,参考温度Tref=273K其逆幂律指数为s=0.74,NCCR常数为1.02029,气体常数为296.8 m2/(s2·K),普朗特常数Pr=0.72,气体比热比 γ=1.4,参考黏性ηref=1.656×10-5N·s/m2.数值模拟的计算状态均与文献[29]中DSMC 的计算状态一致[29].具体来流参数见表1.

表1 流动状态Table 1 Flow state

图1 给出了Kn分别为0.002,0.01 和0.05 时NCCR 模型、NS 方程和DSMC 模拟得到的驻点线对比曲线.可以看出在连续流条件下,NCCR 模型计算结果同NS 方程数据保持一致,且两种方法计算结果同DSMC 数据也保持一致.在非连续流区域,NCCR 模型计算结果同DSMC 数据更为吻合、误差更小,NS 方程结果与DSMC 模拟结果的偏差随流动稀薄程度的增加而增加,流动越稀薄,NS 方程的准确性越差.通过此算例,验证了NCCR 模型在稀薄流动领域能获得比NS 方程更为准确、更符合物理的数值解,同时也证明了NS 方程线性本构模型在高努森数稀薄流动领域的不适用性.

图1 不同努森数条件下圆柱沿驻点线温度分布Fig.1 Temperature distribution of cylinders in different Kn along the stagnation line

图2 给出了Kn=0.002 连续流条件下圆柱模型壁面摩擦、热流和压力系数分布,NCCR 模型、NS 方程及DSMC 数据基本一致.证明在连续流区域NCCR 模型计算结果能够回归到NS 方程结果上.图3～图4 为Kn=0.01,0.05 时圆柱模型壁面摩擦、热流、压力系数的DSMC 数据、NCCR 模型和NS 方程的结果对比.从连续流过渡到滑移流的过程中可以看出,NCCR 模型同NS 方程计算结果出现差距,且随着Kn数的增大,NCCR 模型同NS 方程之间的差距逐渐增大,NCCR 模型计算结果比NS 方程更贴合DSMC 数据结果.随着来流稀薄程度的增加,壁面热流系数和壁面压力系数的变化较小,壁面摩擦系数的变化最为明显.此时NCCR 模型与NS 方程计算结果的差距进一步扩大,从结果上看,NCCR 模型仍然比NS 方程更为贴近DSMC 的仿真数据.NCCR 模型的计算结果同DSMC 的仿真数据之间仍有部分差异,这可能是由于NCCR 模型为降低收敛难度而对某些项简化导致了计算结果精度的降低,在后续工作中将进一步开展研究.

图2 Kn=0.002 时物面系数分布Fig.2 Surface coefficient distribution when Kn=0.002

图3 Kn=0.01 时物面系数分布Fig.3 Surface coefficient distribution when Kn=0.01

图4 Kn=0.05 时物面系数分布Fig.4 Surface coefficient distribution when Kn=0.05

3 尖化前缘气动加热计算

在连续流域,前缘的驻点热流密度可以通过工程中常用的Fay-Riddell 公式进行预测,但在尖化前缘驻点区域发生局部稀薄效应时,Fay-Riddell 公式预测值将偏离真值[30].本文选择前缘半径R=0.5 mm 的飞行器,尖化前缘外形如图5 所示.通过分别对比连续流和滑移流域NCCR 模型、NS 方程及尖化前缘风洞试验结果,分析飞行器的尖化前缘区域是否出现局部稀薄流动,并探究NCCR 模型在计算局部稀薄流动方面的准确性.

图5 模型示意图Fig.5 Model diagram

模型长度为640 mm,尾部宽度为616.78 mm,前缘半径0.5 mm,尾部高度113.35 mm.

风洞试验在中国科学院力学研究所高温气体动力学国家重点实验室JF8A 和JF10 高超声速风洞中进行.试验模型的来流条件见表2,Ma=8.0 的飞行条件在JF8A 中试验[31],JF10 风洞中进行Ma=10.0 飞行条件试验[32],后续计算模型的流动参数同风洞试验参数保持一致.

表2 流场状态参数Table 2 Flow field status parameters

3.1 33 km 处高超声速尖化前缘连续流动效应分析

等效高度33 km 飞行条件下,前缘半径R=0.5 mm 模型的尖化前缘局部Kn数为0.007,处于连续流区域,计算条件为U=1190.25 m/s,Ma=8.0,T=55.07 K,Tw=300 K,P=798.95 Pa.计算仿真模型各项尺寸同试验模型保持一致.图6 对比了NCCR模型与NS 方程计算的沿驻点线温度云图,两种计算方法的结果基本吻合、数值模拟结果保持一致.

图6 驻点附近的温度对比(Ma=8)Fig.6 Comparison of the temperature near the stagnation point (Ma=8)

首先,为了消除计算网格对计算结果的影响,采用3 套不同分辨率的网格进行网格收敛性研究.相关网格信息由表3 给出.图7 给出的表面热流系数分布情况可以看出,细网格2 和网格3 计算结果较为吻合,粗网格结果表现出一定差异.为最大化提升计算效率并降低收敛因素,本算例采用网格2 作为模拟计算模型.

图7 不同网格分辨率下Z=0 m 处壁面热流系数分布Fig.7 Distribution of heat flux coefficient at Z=0 m under different grid resolutions

表3 网格无关性对比Table 3 Mesh independent contrast

壁面热流系数由下式计算所得,其中q为表面热流密度

图8 对比了前缘半径R=0.5 mm 模型对称面中心线上NCCR 模型和实验结果的壁面热流系数,在连续流区域,根据公式计算驻点热流系数实验值为0.026 98,NS 模型计算的驻点热流系数为0.026 4,偏差为 2.15%,NCCR 模型计算的驻点热流系数为0.026 49,偏差为1.81%,Fay-Riddell 公式计算的驻点热流系数值约为 0.028 14,偏差为 4.3%.3 种计算方法同实验值偏差均保持在5%以内,证明在33 km高度,Ma=8.0 来流条件下飞行器尖化前缘区域并未出现局部稀薄气体效应,且在连续流域NCCR 模型计算结果同实验值基本一致.

图8 Z=0 处模型的迎风面与背风面物面热流系数分布(Ma=8)Fig.8 The distribution of surface heat flux coefficient at Z=0 m(Ma=8)in windward side and leeward side

因模型下表面为迎风面,上表面为背风面,故尖化前缘构型的下表面壁面热流系数大于上表面的壁面热流系数.从图8 中可以看出背风面的壁面热流实验值与数值模拟值保持一致.迎风面的前半段部分,实验值与NCCR 模型计算值吻合,但在迎风面尾部存在偏差,偏差产生原因可能是迎风面尾部壁面发生转捩出现湍流,引起壁面与气体分子间的额外能量输运,导致壁面热流系数偏高,而本文NCCR 模型在计算时均使用层流模型,因此可能在湍流区NCCR 模型与实验值之间存在偏差.

图9 是前缘半径R=0.5 mm 模型Ma=8.0 条件下,单侧尖化前缘热流系数分布曲线,考虑到风洞试验的误差,对比时选择实验值的 ± 10% 作为偏差带的上下限.在尖化前缘区域,各点的热流系数值大致在试验值偏差带内,同实验值的吻合性较好.

图9 尖化前缘区域壁面热流系数分布(Ma=8)Fig.9 Heat flux coefficient distribution on sharpened leading edge(Ma=8)

图10 是模型横切对比图,对比Ma=8.0 来流条件下X=0.185 m 处上表面的壁面热流系数.NS 方程、NCCR 模型计算结果同实验值均保持一致.

图10 X=0.185 m 处物面热流系数分布(Ma=8)Fig.10 The distribution of surface heat flux coefficient at X=0.185 m(Ma=8)

图11 对比距模型对称面Z=0.04 m 处纵切面的物面热流系数分布.模拟曲线同实验值基本保持一致.此切面上驻点热流系数为0.014 26,NCCR 模型计算的驻点热流系数为0.015 47,偏差为8.48%,NS 模型计算的驻点热流系数为0.015 48,偏差为8.55%.

图11 Z=0.04 m 处物面热流系数分布(Ma=8)Fig.11 The distribution of surface heat flux coefficient at Z=0.04 m(Ma=8)

3.2 60 km 处高超声速尖化前缘局部稀薄气体流动效应分析

60 km 等效高度时,前缘半径R=0.5 mm 模型尖化前缘局部努森数为0.23,属于过渡流域,计算条件为U=3162.08 m/s,Ma=10.0,T=248.76 K,Tw=300 K,P=23.56 Pa.计算仿真模型的各项尺寸同试验模型保持一致.为了检验非线性本构模型自身对稀薄非平衡现象的捕获能力和准确性,本文在计算过程中壁面采用无滑移等温壁.

为了消除网格分布对计算结果的影响,采用3 套不同分辨率的网格进行网格收敛性研究.网格信息由表4 给出.图12 给出的驻点热流系数分布情况可以看出,网格2 和网格3 计算结果较为吻合,网格1 结果表现出一定差异.网格1 计算驻点壁面热流系数为0.630 56,网格2 计算驻点壁面热流系数为0.633 06,网格3 计算值为0.634 55,为最大化提升计算效率并降低收敛因素,本算例采用网格2 作为模拟计算模型.

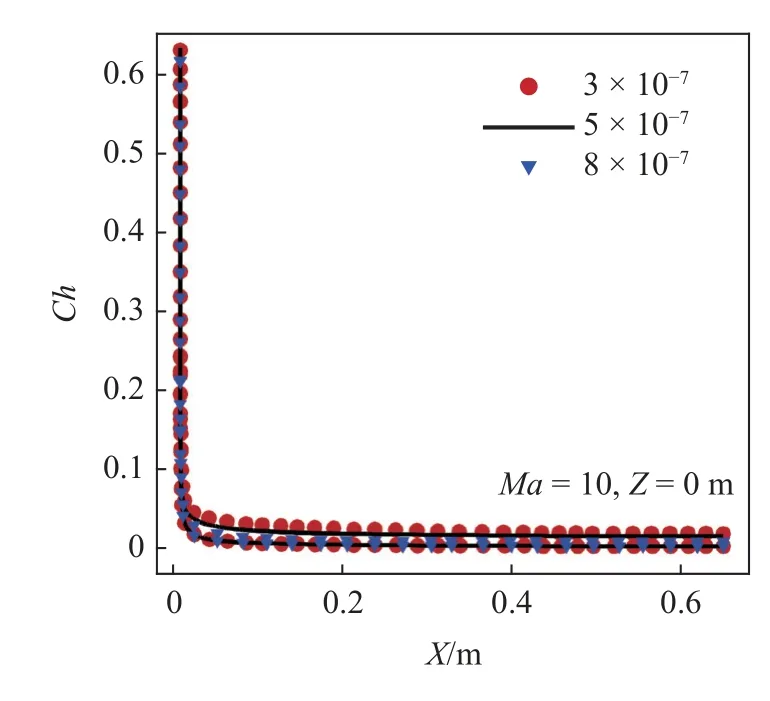
图12 不同网格分辨率下Z=0 m 壁面热流系数分布Fig.12 Distribution of heat flux coefficient at Z=0 m under different grid resolutions

表4 网格无关性对比Table 4 Mesh independent contrast

图13 对比了NCCR 模型和NS 方程计算的沿驻点线流场温度分布曲线,NCCR 模型与NS 方程计算的激波位置、激波层内温度分布和温度峰值存在差异.在60 km 高度时,尖化前缘驻点存在局部稀薄气体效应,NCCR 模型不仅能修正存在局部稀薄效应的驻点热流密度,而且计算沿驻点线温度分布结果更接近真实物理解.

图13 两种方法计算沿驻点线温度分布(Ma=10)Fig.13 Temperature distributions along the stagnation line (Ma=10)

图14 对比了NCCR 模型与采用无滑移边界条件的NS 方程分别计算前缘半径R=0.5 mm 飞行器的驻点前温度云图,因尖化前缘处于过渡流区域,NS 方程计算结果在此区域内已不再准确,对比发现NCCR 模型计算的驻点前区域,激波、激波脱体区域、边界层三者之间的界限逐渐模糊和重合,NCCR模型计算的激波层内温度峰值要比NS 方程的峰值要低,激波层内部温度变化比NS 方程更加均匀.许多已发表的研究指出NCCR 模型能够准确描述过渡流区的高超声速流动[16,33],证明NCCR 模型在连续/稀薄耦合流动求解中的潜力和工程价值.

图14 驻点附近的温度对比(Ma=10)Fig.14 Comparison of the temperature near the stagnation point(Ma=10)

图15 对比了前缘半径R=0.5 mm 模型的NCCR模型和实验结果的壁面热流系数,高超声速飞行器的热防护系统设计初期会将局部高热流密度作为设计重点,而通常情况下,驻点热流密度属于模型的热流密度峰值,因此我们重点关注驻点热流密度的偏差情况.在过渡流区域,驻点实验热流系数为0.474 88,NS 方程计算驻点热流系数为0.633 06,与实验值偏差为33.31%;NCCR 模型计算的驻点热流系数为0.530 76,偏差为11.77%;而Fay-Riddell 公式计算的驻点热流系数值约为0.615 11,偏差为29.5%.在非驻点区域局部稀薄效应影响较小,NCCR 模型计算结果同实验值基本保持一致.在图14 中激波层内温度分布及温度峰值的计算上NCCR 模型的结果更准确和可靠.

图15 Z=0 m 处迎风面与背风面物面热流系数分布(Ma=10)Fig.15 The distribution of surface heat flux coefficient at Z=0 m(Ma=10)in windward side and leeward side

通过图15 壁面热流系数的分布可以看出: 除驻点附近热流系数外,NCCR 模型与NS 方程计算迎风面与背风面热流系数与实验值基本一致.证明壁面除前缘外的部分局部稀薄气体效应较弱,NS 方程的计算结果能够满足精度要求.

图16 对比了距模型对称面Z=0.02 m 处尖化前缘模型纵切面的物面热流系数分布.存在局部稀薄效应的尖化前缘区域中,NS 方程计算驻点热流系数为0.491 43,NCCR 模型计算驻点热流系数为0.414 54,NS 方程计算结果同NCCR 模型偏差为18.55%.而非前缘区域流动处于连续流状态,NS 方程同NCCR模型结果与实验值基本保持一致.

图16 Z=0.02 m 处物面热流系数分布(Ma=10)Fig.16 The distribution of surface heat flux coefficient at Z=0.02 m(Ma=10)

4 结论

本文针对尖化前缘构型在高超声速连续/稀薄流中的气动加热问题开展数值计算研究和风洞实验验证.根据实验来流条件,借助NCCR 模型对尖化前缘构型在Ma=8,10 的0°攻角状态下的物面热流系数进行了数值计算,并与风洞试验结果进行对比验证.通过对比物面热流系数和沿驻点线温度分布,检验了NCCR 模型相比于NS 方程在计算三维高速局部稀薄流动中的改善水平.本文研究结论总结如下.

(1)飞行器尖化前缘处于低空连续流条件下,驻点区域局部稀薄气体效应并不明显,NCCR 模型与NS 方程计算结果同实验值保持一致,偏差均保持在5%以内.

(2)飞行器尖化前缘处于中高空来流条件时,尖化前缘的局部稀薄气体效应随高度增加逐渐显著,NCCR 模型不仅能够修正局部稀薄流动区域的壁面热流系数值,而且近壁面流场内参数计算的结果更接近真实物理解.

(3)在等效高度60 km,来流马赫数Ma=10.0的条件下,NS 方程计算驻点热流系数偏差为33.31%,NCCR 模型计算驻点热流系数偏差为11.77%;在相同计算条件下,不考虑边界条件带来的影响,NCCR模型计算驻点热流系数在误差允许范围内同试验值更为接近,体现出非线性本构方程求解稀薄区域流动的优势.