水翼端部间隙泄漏流的压降及黏性损失机理1)
2023-11-16向秋杰陈为升黎耀军刘竹青
向秋杰 陈为升 黎耀军,†,2) 刘竹青,†,
*(中国农业大学水利与土木工程学院,北京 100083)
† (北京市供水管网系统安全与节能工程技术研究中心,北京 100083)
** (东北农业大学水利与土木工程学院,哈尔滨 150030)
引言
轴流式水力机械转子叶顶间隙产生的泄漏流,在间隙区形成间隙泄漏涡(tip leakage vortex,TLV)、间隙分离涡(tip separation vortex,TSV)和诱导涡(induced vortex,IV)等复杂涡系结构[1-2].间隙泄漏流产生的黏性损失和压降,是导致机组水力性能下降和间隙区空化的主要因素.探明间隙泄漏流动的特征,揭示间隙区黏性损失和低压的产生机制及影响因素,对间隙泄漏流动控制及高性能水力机械研发具有重要意义.
间隙区黏性损失与涡系结构的湍流特征密切相关[3-4].Lakshminarayana[4]的研究发现,轴流式叶轮叶尖涡系结构存在强烈的速度脉动,且黏性损失与表征速度脉动的湍动能成正比,并提出了基于湍动能的黏性损失定量计算模型;速度脉动是影响间隙流动黏性损失的重要因素[5].You 等[6-7]基于LES结果,分析了叶栅间隙流中湍动能生成与黏性损失的关联,发现了间隙射流和TLV 中造成黏性损失的主导速度梯度.从能量转换的角度,流场中的黏性损失本质上为压能和动能在流体黏性作用下转换为内能[8-10].在忽略换热的情况下,黏性损失体现为平均流动黏性耗散和湍流耗散,前者表征流体黏性导致的平均流动动能(mean-flow kinetic enerty,MKE)向内能转化,后者则为湍流动能(turbulent kinetic enerty,TKE)经由耗散尺度湍流最终转化为内能[8].根据流场中平均流动动能、湍动能和内能间的转换关系,湍流耗散对应的黏性损失来源于大尺度湍流与平均流动相互作用产生的湍动能,因此,通过量化平均动能向湍动能的转换,即可获得湍流耗散对应的黏性损失[11-12].
间隙泄漏流也是导致压降及空化的重要因素.在叶栅端部间隙流中,TLV 内的静压显著下降,并伴随强烈的湍流脉动[1],且间隙区最低静压位置与TLV涡心趋于一致;在轴流转子叶尖间隙流中,尽管泄漏流导致的局部压降对表征流场全局压力特性的空化数并不敏感[13],但压降与叶尖间隙区的流动特性密切相关,空化主要发生在TLV 和TSV 区域.此外,间隙形状也是影响间隙涡结构及间隙区压降的关键因素,对于水翼端部间隙流,增加翼端边缘倒圆半径,可有效降低间隙内TSV 区域发生空化的风险,但TLV 内的静压下降幅度则明显增大[14].对于不可压缩流动,流场中局部位置的静压与速度变化直接相关,局部压降对应静压能向动能的转化[15].因此,阐明间隙泄漏流中压能与平均流动动能和湍动能的转换及输运关系,为揭示间隙区流动黏性损失和压降的形成机制提供了可能.
流体机械叶顶间隙流的能量转换过程复杂,考虑到旋转机械轮缘间隙流动和翼型端部间隙流的涡结构具有相似性[16],因此本文以NACA0009 钝尾缘水翼为研究对象,其相对简单的涡系特征,更利于阐释间隙区的能量转换及压降特性.为充分求解间隙区流场的湍流特征,采用可解析含能大尺度湍流结构的超大涡模拟方法(very large eddy simulation,VLES)方法,对翼端间隙流场进行非定常数值模拟;基于平均流动黏性耗散、TKE 生成、压能和MKE输运间的平衡分析,提出黏性损失和压降的定量计算和评估模型,分析翼端间隙流动特性,揭示间隙区压降和黏性损失的形成机制.
1 计算模型与方法
1.1 研究对象与物理模型
本文研究对象为NACA0009 钝尾缘对称水翼[17],水翼端部与静止壁面的间隙τ=0.02c.基于来流速度u∞=10 m/s 和水翼弦长c=100 mm 的雷诺数Re=1.0×106,来流攻角为10°.如图1 所示,计算域沿流向长10c,垂直于流向的断面为1.5c×1.5c,水翼中心距计算域入口为5.1c.
1.2 湍流模型
为准确解析翼端间隙区流场结构,采用可求解部分湍流脉动的VLES 方法[18-21]进行流场计算.VLES 通过引入湍流尺度求解控制函数Pr,对RANS方法湍流模型的雷诺应力进行修正,以降低湍流模化的比例,实现对流场中大尺度湍流结构的直接求解,近年来该方法在复杂工程湍流的模拟中得到成功应用[3,22-23].由于RANS 方法的SSTk-ω模型考虑了逆压边界层中湍流剪切应力传输效应,可以有效预测逆压梯度条件下的流动分离,在复杂工程湍流求解中应用广泛[24-26],因此,本文以SSTk-ω模型为基础构造VLES 湍流模型.根据Boussinesq 假定,对雷诺应力张量的调整可以近似等效为对湍流黏度的调整.VLES 模型的湍流黏度为
式(1)中,控制函数Pr可实现VLES 从RANS到DNS 间的过渡,当网格分辨率足以求解全部湍流时,即Pr趋近于0,VLES 类似于DNS;在粗网格或雷诺数无限大条件下,Pr趋近于1,VLES 等效于RANS方法;Pr介于0~1 之间时,VLES 则类似于LES 的亚格子尺度模型(SGS)[28],可以直接求解含能尺度湍流结构.本文采用文献[28]给出的VLES 模型控制函数Pr
其中,Lc为网格长度尺度,Li为湍流积分长度尺度,Lk为Kolmogorov 长度尺度,模型系数β=2.0×10-3,n=2.
1.3 网格划分和求解设置
采用六面体结构化网格离散计算域,为提高近壁边界层内的网格质量,水翼周围网格由两层O 型网格拓扑构成.间隙区采用多个O-H 型分块网格填充,水翼上游及下游采用H 型网格.采用了3 套网格进行网格收敛性分析,网格单元总数分别为276万、633 万和1010 万,近壁面第1 层网格y+平均值分别为9.6,3.4 和1.5.网格总数为1010 万的网格方案,翼端间隙内采用了55 层网格,翼端间隙区x-y平面内的网格结构如图2 所示.

图2 间隙内网格分布(x-y 平面)Fig.2 Grid in the tip-gap (x-y plane)
采用CEL 语言将VLES 湍流模型集成至ANSYS CFX 软件,对水翼间隙流进行非定常数值模拟.计算域入口给定平均流速u∞,入口湍流强度为2%,计算域出口设置静压为1.013×105Pa.计算域边壁及水翼表面均设为无滑移壁面.采用分离求解法对不可压缩控制方程进行求解.对流项离散采用高阶精度离散格式,非定常求解的时间推进采用二阶后向欧拉方格式.无量纲时间步长t*=1.5×10-3c/u∞,对应的库朗数最大值小于2.
1.4 黏性损失计算模型
流场中的瞬时速度ui可分解为VLES 非定常计算所得瞬时速度与模化的湍流速度脉动.在大尺度时间平均流场中,可进一步分解为时间平均速度 〈〉 和直接求解的湍流速度脉动;瞬时压力p也可进行类似分解,如下式
在时间平均流场中,计算域单位时间内的黏性损失为流入与流出计算域边界的能量差,即计算域进、出口的总压差与流量的乘积.考虑到壁面不存在能量通量,因此,黏性损失可以通过积分流场边界的能量通量计算,根据高斯-格林公式,单位时间内给定区域的黏性损失(总能量损失)为
式中,S和V分别表示积分区域的边界和体积;nj表示边界的单位外法向量的j向分量.
式(4)表明,单位质量流体的黏性损失可表示为压能EP=〈〉/ρ 和平均流动动能MKE=0.5〈〉〈〉空间变化的体积分,且式(4)右侧被积函数分别为平均流动动能输运方程的源项和对流项.因此,流场中压能及平均流动动能的空间分布及转换可通过平均流动动能输运方程描述,如下式[11]
值得注意的是,SMKE表征速度-压力相互作用导致的平均流动动能输运,为MKE 输运方程的源项,当流场局部位置SMKE取负值时,平均流动动能增加(CMKE取正值),对应位置的压力下降,因此,对流效应可看作是导致静压变化的直接因素.由于εmean,PTKE和DMKE均仅直接影响MKE,间接影响压能的分布,因此可以看作是导致流场压力变化的间接因素.
由式(3),在VLES 中,与平均速度 〈〉 对应的脉动速度包含直接求解的部分和模化的部分,因此,TKE 和PTKE对应可分解为直接求解部分(TKEres和PTKE-res)和模化部分(TKEmod和PTKE-mod),如下[26]
基于上述分析,式(5)所示的流场中压能、平均动能和内能的转换关系可总结为图3[29-30].
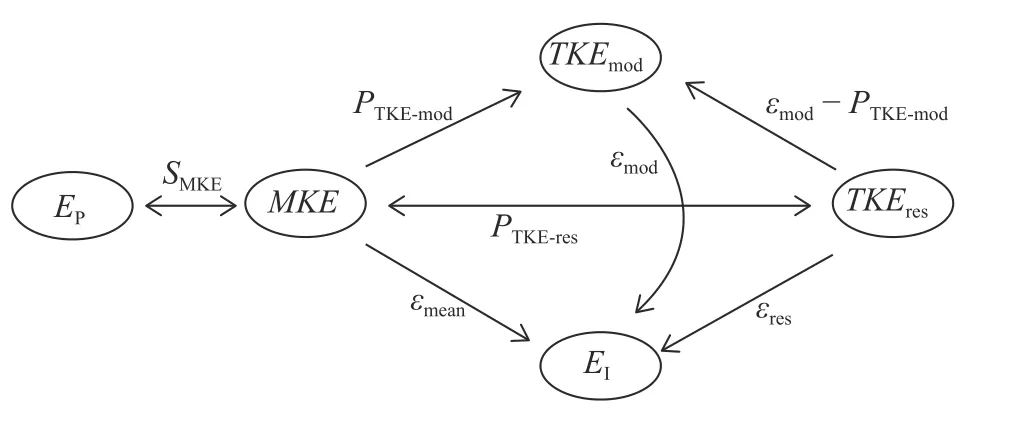
图3 VLES 模型计算流场中的能量转换关系Fig.3 The energy conversion process in flow field of the VLES results
图3 中εres和εmod分别表示直接求解的湍流耗散率和模化的湍流耗散率,εmod-PTKE-mod表示未直接求解的湍流导致的TKEres向TKEmod的转换率.
可见,流场中黏性损失存在两种产生机制,即平均流动黏性耗散(εmean)和湍流耗散(εmod和εres),前者直接作用于MKE,导致MKE 的变化,而湍流耗散导致的能量损失则来源于流场中生成的湍动能.因此,流场中给定区域的黏性损失ΔVL,包含平均流动黏性耗散损失ΔMVL和湍流耗散损失ΔTVL,其大小分别通过积分εmean和PTKE获得,即
2 结果与讨论
2.1 网格无关性分析与计算模型验证
采用拓扑结构相同的3 套网格(网格数分别为276 万、633 万和1010 万)进行了流场计算,通过与文献[17]实验结果的对比,验证计算模型的合理性和计算结果的可靠性.图4 所示为3 种网格方案下所得水翼下游x/c=1 位置处的平均流向速度 〈〉 和垂向与展向的合速度 〈〉 的分布.从图4 可以看到,数值模拟所得速度分布整体上与试验结果吻合良好.网格数量为633 万和1010 万的网格方案,计算所得对应速度的分布趋于一致.
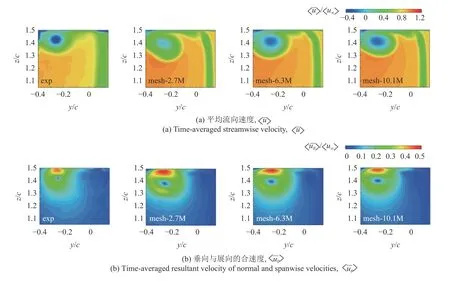
图4 不同网格所得时均速度和试验值的对比(x/c=1)Fig.4 Comparison of the predicted mean velocity with the experimental results for different meshes (x/c=1)
图5 给出了不同网格方案计算所得模化的湍流动能TKEmod与总湍流动能TKE的比值,fk=TKEmod/TKE,fk是评估湍流求解程度的典型指标[31].可以看出,fk随着网格分辨率的增加而减小,表明所采用的VLES 方法在精细网格条件下大幅降低了模化的湍流占比.图5 显示,网格单元为1010 万的网格方案,最大fk约为0.3,该网格方案可以较充分求解水翼翼端间隙区域湍流.因此,后续将基于该网格的计算结果,分析翼端间隙区的黏性损失和压力变化.
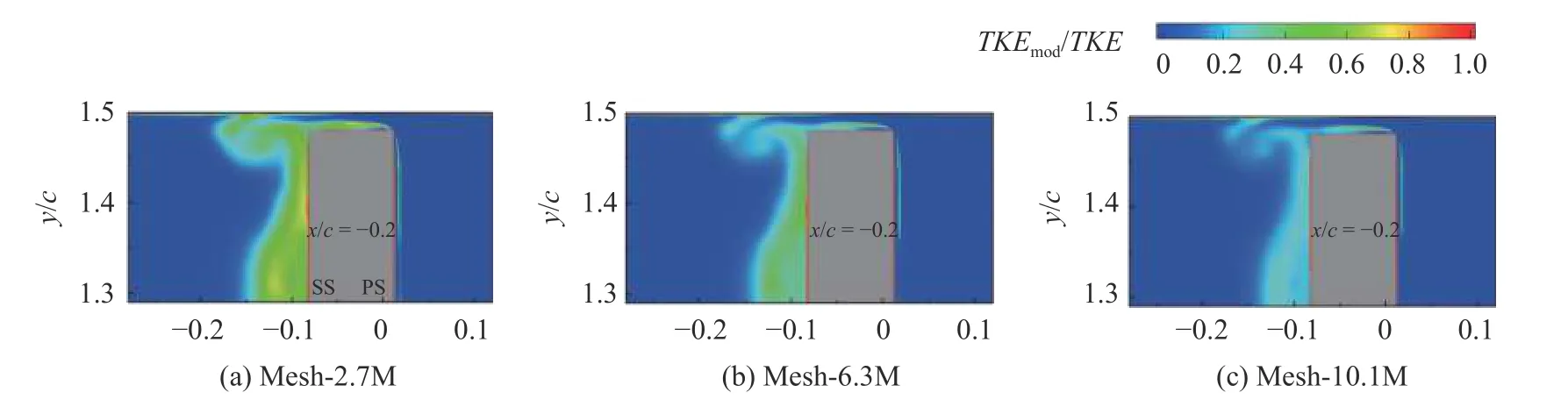
图5 不同网格计算所得模化的湍动能占比(TKEmod/TKE)Fig.5 Ratio of modeled to total turbulent kinetic energy obtained by different meshes (TKEmod/TKE)
2.2 间隙区流动结构和压力分布
图6 所示为以Q准则显示的间隙区涡结构,以及间隙区流向x/c=-0.4,-0.2,0,0.2位置处流向平均涡量〈〉 和平均静压系数的分布(pinlet为计算域入口静压).从图6(a)可以看到,翼端间隙内靠近水翼端壁形成了分离涡结构(TSV);间隙泄漏流通过翼端间隙后在水翼吸力面侧(SS)形成间隙射流,其强卷吸效应与吸力面侧主流相互作用,发展为间隙泄漏涡(TLV);TLV 诱导端壁边界层分离,伴随形成与TLV 旋转方向相反的诱导涡(IV).图6(b)所示的流向涡量 〈〉 的分布云图清晰显示了y-z平面内的二维涡旋结构,在TLV,TSV 和间隙射流区域内,〈〉 为正且其量值沿流向逐渐减小;TLV 对端壁边界层卷吸作用诱导形成的IV,其旋转方向与TLV 相反,因此IV 区域内 〈〉 为负[32];图6(b)中采用 〈〉=0 的等值线(白色实线)表征IV 的外边界.图6(c)的平均静压分布表明,翼端区域内的低压区主要位于水翼前半段的TSV和TLV 区域内,TSV 和TLV 是导致翼端间隙区局部压降的主要流动结构.

图6 翼端间隙区时间平均流动特征Fig.6 Mean-Flow Characteristic around the tip-clearance
图7 展示了流向x/c=-0.4,-0.3,-0.2,-0.1 位置处间隙区的平均速度分布,图中叠加了流向涡量等值线以显示TLV 及IV 等涡结构的位置,其中白色等值线对应的涡量等于0.从图中可以看到,受翼端间隙泄漏流的影响,翼端TSV 区域的流向平均速度 〈〉 趋于0,〈〉 是水翼吸力面侧的主导速度分量,且 〈〉 在TLV 区域存在明显的法向速度梯度和展向速度梯度.随着TLV 沿流向发展,〈〉 峰值位置逐渐偏离TLV 涡心向水翼吸力面偏移.翼端间隙内,法向平均速度 〈〉 占主导,且存在明显的展向梯度.间隙区不同流向位置的展向速度 〈〉 均明显小于流向和法向速度.图7 表明,间隙区不同位置的主导速度分量不同,因此,间隙区将形成复杂的剪切流动,流场中速度梯度显著增大.由于流场中的压降和湍动能生成等能量转换过程与速度梯度密切相关,因此间隙区涡系结构伴随的流动掺混及强速度梯度将增加间隙区平均动能的损失.
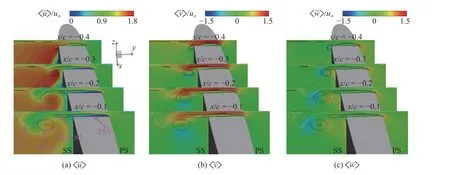
图7 间隙区平均速度分布Fig.7 The distribution of time-averaged velocity in the tip-clearance region
2.3 TSV 的压降
从能量转换的角度看,式(5)所示MKE 输运方程中,SMKE表征了平均静压在空间的变化,代表流场中压能与平均流动动能的相互转换,其受到对流作用(CMKE)、黏性耗散(εmean)、湍动能生成(PTKE)和平均流动动能输运(DMKE)的共同影响.图8 给出了不同流向位置处的SMKE,CMKE,εmean,PTKE及DMKE的分布云图,以评估平均动能MKE 转换过程的不同效应对间隙区压力变化的影响.图中●和▲分别对应TLV 和TSV 区域内的最低压力(涡心)位置,黑色实线为以TLV 涡心涡量的10%划定的TLV 影响范围,白色实线为10%TSV 涡心涡量的等值线,以展示TSV 的影响范围.

图8 平均流动动能输运方程各项的分布Fig.8 The distribution of terms of the mean-flow kinetic energy transport equation
图8(b)显示,在水翼端面靠近压力侧(PS),CMKE的取值显著高于其他区域,这是因为水翼正背面压差导致的间隙泄漏流动,在该区域形成了流动加速,对流效应显著增强,导致静压能转换为MKE(对应区域内SMKE为负值,如图8(a)所示).在TSV 区域(白色实线),CMKE以负值为主,且CMKE<0 的区域内SMKE>0,表明TSV 区域的速度-压力相互作用对MKE 有负贡献,MKE 转换为压能,促进压力升高,有利于减少TSV 内的压降.此外,TSV 区域PTKE为正值,湍动能生成将消耗MKE,由于SMKE为MKE 输运方程的源项,压能与MKE 相互转化,因此,从压力变化的角度看,PTKE对应的湍动能生成将间接消耗静压能,导致TSV 区域的静压下降.从图8 所示的MKE输运方程不同项分布与量值上看,PTKE明显高于εmean和DMKE,表明湍动能的生成是影响TSV 区域压降的主要因素.另外,随着流动向下游发展,PTKE的量值和取高值的区域范围逐渐减小,对静压能的消耗降低,这与TSV 内静压随流向增加逐渐升高的趋势相吻合.
为进一步探究TSV 流动中湍动能生成作用的主导因素,将PTKE分解为如式(10)所示的9 个分量Pij,以分析不同分量对湍动能生成作用的影响.
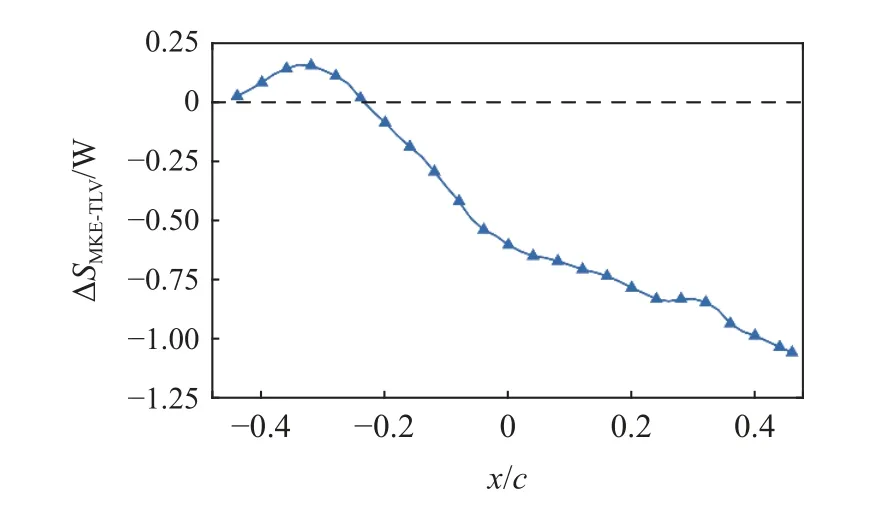
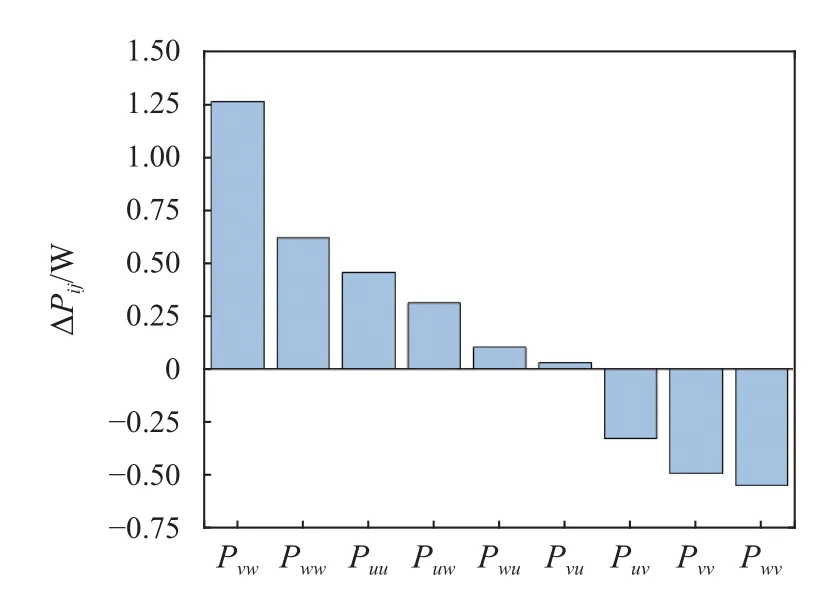
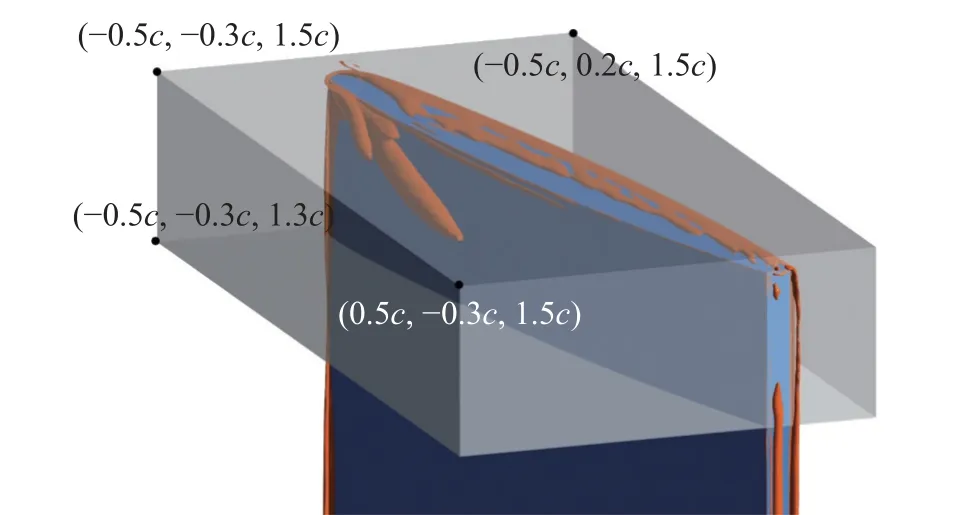
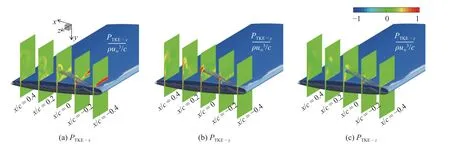
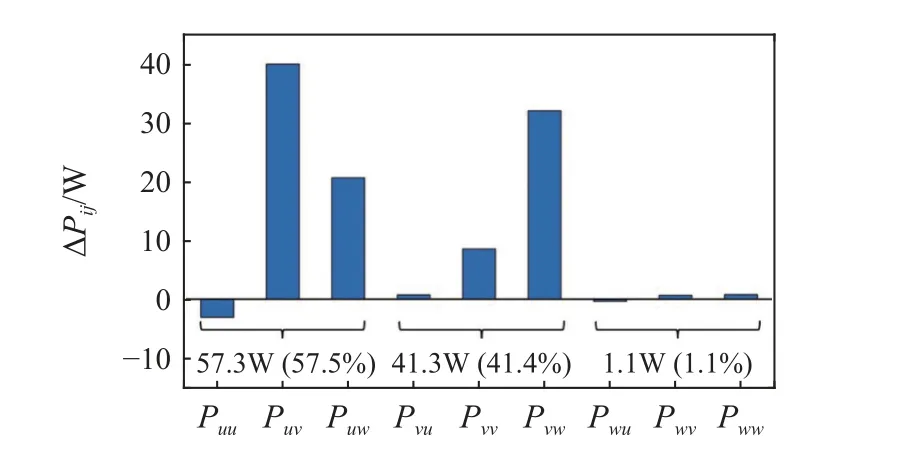
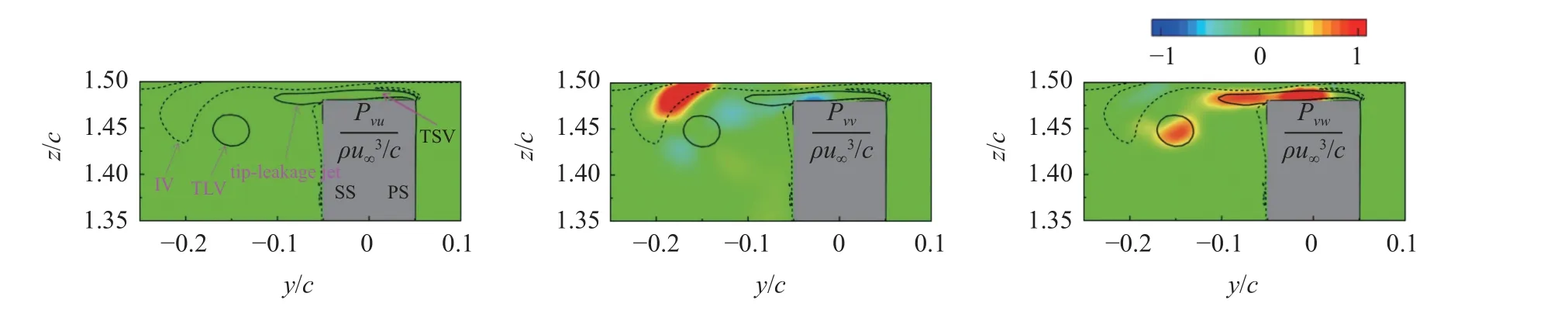
TSV 区域内湍动能生成作用随着流向增加而逐渐减弱,不失代表性,选取流向x/c=-0.4 位置处通过TSV 涡心的展向特征线(y/c=-0.066,1.48 图9 湍动能生成项分量Pij 分布Fig.9 The distribution of turbulent kinetic energy production term components,Pij 从图8 可以看到,与静压变化平衡的CMKE,εmean,PTKE和DMKE在TLV 区域内的分布并无明显的规律.为探明导致TLV 中心压力下降的机理和主要影响因素,本节定量分析TLV 的压力变化特性. 在以TLV 涡心涡量10% 的等值线为边界的TLV 区域(见图8)内对SMKE进行积分,获得单位时间内TLV 区域沿流向每0.01c间隔长度的压能转换量ΔSMKE-TVL,如下所示 式中,ATLV表示y-z平面内TLV 区域的面积.由于SMKE表征速度-压力相互作用对应的动能输运,其物理意义为平均静压强做功,可看作MKE 输运方程的源项,SMKE为负表示消耗静压能,因此,ΔSMKE-TVL大于零表示压能向平均动能转换,反之表示平均动能向压能转换. 图10 所示为TLV 边界内ΔSMKE沿流向的分布.从图中可以看到,TLV 区域ΔSMKE-TVL>0 的范围位于靠近水翼头部的约前25%弦长区域(-0.5 图10 TLV 区域内压能转换量ΔSMKE-TVL 沿流向的分布Fig.10 The pressure energy conversion,ΔSMKE-TVL,in the TLV region along the streamwise direction 由于ΔSMKE>0 对应为压能向MKE 的转换,因此深入分析ΔSMKE>0 的TLV 区域的能量转换过程,有助于揭示TLV 涡心低压的形成机制.为此,在ΔSMKE-TVL>0 的区域,对方程(5)中的CMKE(对流作用)、PTKE(湍动能生成作用)、εmean(平均流动黏性耗散作用)和DMKE(能量输运作用)进行积分,分别获得ΔSMKE-TVL>0 区域的能量转换及输运量ΔCMKE-TVL,ΔTVLTVL,ΔMVLTVL和ΔDMKE-TVL,以定量分析能量平衡方程中不同能量转换和输运作用对TLV 压降的影响程度.表1 所示为TLV 内ΔSMKE-TVL>0 的区域(图10)不同能量转换和输运作用对压能转换的贡献占比.可以看到,CMKE,PTKE和DMKE分别代表的对流效应、湍动能生成及扩散效应(空间再分布)是影响TLV 区域内压降的主要因素,其中,湍动能生成对TLV 区域的压力下降贡献率超过57%,是TLV 内压力下降的主导因素. 表1 TLV 区域内压降产生因素的贡献率Table 1 Contributors of the pressure drop in the TLV region 由于湍动能生产与速度梯度密切相关(见式(10)),为进一步探明TLV 中压降的主导速度梯度,在TLV内ΔSMKE-TLV>0 的区域,对Pij进行积分,获得该区域湍动能生成项PTKE各分量Pij对应的湍动能生成量ΔPij,如图11 所示,以分析不同分量对湍动能生成和TLV 内压降的贡献.可以看到,Pvw和Pwv分别是湍动能生成的最主要促进因素和抑制因素,且ΔPvw的量值明显高于PTKE其余分量,因此Pvw是影响TLV 内ΔTVL变化的最主要因素.You 等[6]指出,在湍动能生成项中,速度梯度是湍动能生成的主要作用因素,根据式(10),可以认为TLV 内垂向速度的展向梯度 ∂ 〈〉/∂z是影响湍动能生成(消耗MKE,进而降低压能Ep,导致TLV 涡心压力下降)的最主要速度梯度.基于上述讨论,从流动控制的角度,减小TLV 区域内速度梯度,尤其是降低垂向速度的展向梯度 ∂ 〈〉/∂z,以减少TLV 内的湍动能生成,是减少翼端TLV 压降进而降低空化风险的潜在途径. 图11 湍动能生成项分量Fig.11 Contributions of sub-components of PTKE to TKE production MKE 输运方程的湍动能生成项PTKE及直接黏性耗散项εmean分别对应单位时间内平均流动动能向TKE 的转化率(最终经耗散尺度湍流转化为内能)和不可逆的黏性耗散率,表征因流体黏性导致的黏性损失.为分析间隙区的黏性损失特性,在如图12所示的包含间隙涡系结构的翼端区域(-0.5 图12 翼端黏性损失统计区域Fig.12 Statistics domain of the viscous losses in the tip-clearance region 表2 所示为翼端间隙区的黏性损失,与平均流动黏性耗散εmean对应的黏性损失ΔMVL,占该区域总黏性损失的8.8%;与MKE 转换为TKE 对应的损失ΔTVL,是间隙区能量损失的主要来源,占损失总量的91.2%.可见,水翼端部间隙区复杂的涡系伴随的能量转换是造成黏性损失的主要原因. 表2 翼端区域的黏性损失Table 2 Energy losses in tip-clearance region 上述定量分析表明,与湍动能生成对应的能量损失ΔTVL是翼端间隙区黏性损失的主要来源.由于湍动能生成与速度梯度密切相关(见式(10)),本节分析影响翼端间隙区湍动能生成主要速度梯度,探讨间隙区湍流黏性损失的形成机制和主要影响因素. 图13 翼端间隙区湍动能生成项PTKE 分量的分布Fig.13 The distribution of TKE production term components in the tip-clearance region 为定量分析PTKE各分量对间隙区能量损失的影响和贡献率,统计了PTKE各分量在图12 所示翼端范围内的积分值,即单位时间内PTKE各分量产生的湍动能,如图14 所示.可以看到,间隙区PTKE-x和PTKE-y是生成湍动能的主要因素,分别占该区域内总TKE 生成量的57.5%和41.4%,而PTKE-z生成的湍动能占比仅为1.1%. 图14 PTKE 分量产生的湍动能Fig.14 Contributions of subcomponents of PTKE to turbulent kinetic energy production 值得注意的是,PTKE-x的分量Puv和Puw是湍动能生成的主要贡献因素,其原因是水翼吸力面侧存在明显的流向速度的法向梯度 ∂ 〈〉/∂y和展向梯度∂〈〉/∂z.综合图13 与图14 还可以发现,TLV,IV 和TSV 等间隙区的涡结构,主要通过PTKE-y将平均流动动能转换为湍动能分量,最终形成黏性损失.因此,结合PTKE-y不同分量的分布特征,分析湍动能生成与间隙区流动结构间的联系,可进一步探明间隙区黏性损失的主导因素. 图15 所示为流向x/c=0 位置处PTKE-y分量Pvu,Pvv和Pvw在间隙区的分布.可以看到,Pvu在间隙区流场中均趋近于0,Pvv主要分布于IV 区域,表明Pvv是IV 区域内湍动能生成的主要因素,主导速度梯度为垂向速度的垂向梯度 ∂ 〈〉/∂y;而间隙射流、TSV 以及TLV 对应的湍动能生成则主要受Pvw影响,对应的主导速度梯度为垂向速度的展向梯度 ∂ 〈〉/∂z.结合Pvv和Pvw的数学表达及分布特点,从流动控制的角度,降低TSV 和TLV 内垂向速度的展向梯度 ∂ 〈〉/∂z、减小IV 区域内垂向速度的垂向梯度 ∂ 〈〉/∂y,是降低翼端区域内湍流黏性损失的有效途径. 图15 Pvu,Pvv 和Pvw 分布(x/c=0)Fig.15 The distribution of PTKE components Pvu,Pvv and Pvw at streamwise location x/c=0 本文采用VLES 模型对端部间隙为2%c的NACA0009 水翼翼端间隙流动进行非定常数值模拟,揭示了间隙区涡系结构和主要流动特征,基于考虑压能和平均动能输运的能量损失计算模型,研究了翼端间隙区压降形成机制及黏性损失机理,得到以下主要结论. (1)流场局部压降的产生,与平均流动动能的对流效应、平均流动黏性耗散、湍动能生成和平均流动动能输运相关.基于平均动能输运和流场中的能量转换关系构建的黏性损失计算模型,可分别通过积分平均流动黏性耗散率和湍动能生成率,定量计算平均流动黏性耗散和湍动能耗散对应的黏性损失. (2)翼端间隙泄漏流发展形成间隙泄漏涡(TLV)、间隙分离涡(TSV)和诱导涡(IV);湍动能生成是导致TSV 和TLV 内压降的主导因素,而对流效应和平均动能输运对TLV 内压降也有重要影响;湍动能生成项分量Pvw及对应的速度梯度 ∂ 〈〉/∂z是导致TLV 和TSV 中湍动能生成和压降的主要因素.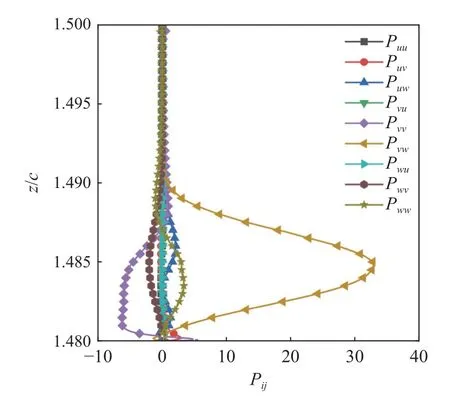
2.4 TLV 的压降

2.5 间隙区黏性损失

2.6 间隙区TKE 生成的影响因素
3 结论
