等截面四点接触球轴承承载能力分析*
2023-11-15刘天宋
张 俊,刘天宋
(江苏联合职业技术学院 常州刘国钧分院,江苏 常州 213000)
0 引言
等截面四点接触球轴承是先进制造业中的重要零件,起到两部件之间旋转和传递载荷的作用,由滚动体、内圈、外圈和保持架等部件组成 ,可同时承受轴向力、径向力、倾覆力矩的综合载荷,广泛用于精密仪器、机床、工程机械、工业机械人等领域。随着先进制造业的高速发展,各行各业对等截面四点接触球轴承的承载能力和可靠性提出了更高的要求[1-2]。
在等截面四点接触球轴承承载能力研究方面,国内外学者通过对一些条件进行简化设置,建立静力学模型,计算结果与实际情况存在一些误差,但可用于等截面四点接触球轴承承载能力研究。轴承静力学分析是以Hertz接触理论作为基础理论,为轴承的设计和分析提供理论支撑。轴承解析计算通常将内圈和外圈假设成刚性体,变形仅发生在滚动体与滚道接触区域,运用赫兹接触理论求解接触区域的力学特性分析[3]。当赫兹接触理论假设不满足时,解析解应用的范围和精度受较大影响,理论结果与实际工程情况存在误差,例如:球式轴承滚球与滚道半径相差小,不满足非协调性接触假设等。
数值计算模型能够有效解决赫兹接触理论带来的误差,而且可以考虑更多的影响因素,计算精度和效率高,但是数值计算模型不同,参数设置、网格大小、算法等对计算结果影响不同,需要进行模型验证。罗继伟等[4]运用赫兹接触理论求解圆锥滚子轴承滚子与滚道接触区域的接触应力。吴飞科等[5]建立数值模型分析不同滚道曲率系数对点接触类型滚动轴承的影响。Houpert[6]对不同轴承受力模型进行分析,提出滚动体计算的新方法,但对深沟球轴承及内圈和外圈不重合的球轴承无法使用。尚振国等[7]建立轴承有限元模型,材料设置为弹性和弹塑性两种,研究不同材料参数的滚动体与滚道接触受载后的变形情况。Khonsari等[8]建立滚球与平板接触有限元模型,将接触区域应力分布与赫兹接触理论结果进行对比,计算结果对比显示两者误差小。Pandiyarajan等[9]建立大直径球轴承接触有限元模型,分析滚球与滚道接触区域的应力分布和变形。
解析计算方法和数值计算方法对等截面四点接触球轴承承载能力计算结果不同,计算结果误差大。本文根据赫兹接触理论提出一种数值模型验证方法,排除数值模型设置对计算结果的干扰,提高数值模型精度。运用验证过的数值模型进行等截面四点接触球轴承承载能力分析,提高等截面四点接触球轴承承载能力计算的精度和效率,对等截面四点接触球轴承设计人员结构设计和优化设计提供重要参考,对工程实际应用具有重要意义。
1 等截面四点接触球轴承承载能力理论计算
1.1 等截面四点接触球轴承结构尺寸
本文以等截面四点接触球轴承作分析,单个滚球与内圈和外圈有四个接触点,如图1所示,虚线为滚球与滚道接触点连线,而且外径与内径比值小,滚球直径小且数量多,横截面和重量一般约为相同内径的标准轴承的20%和5%,可同时承受轴向力、径向力和倾覆力矩的联合作用,整体结构尺寸参数如表1所示。等截面四点接触球轴承的滚球、内圈和外圈材料均为GCr15轴承钢,其弹性模量为207000 MPa,泊松比0.3。等截面四点接触球轴承与深沟球轴承装配方式相同,滚球个数z的约束函数[10]:

表1 等截面四点接触球轴承结构尺寸
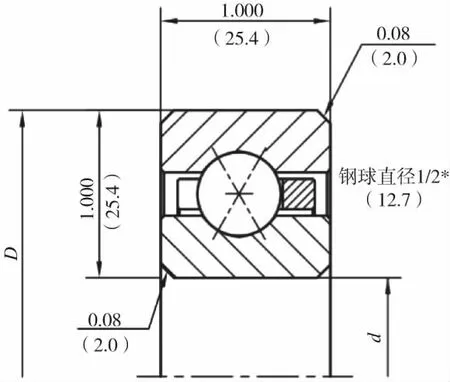
图1 等截面四点接触球轴承结构图
(1)
式中:Dw-滚球直径,Dwp-滚道直径,φmin-最小填球角,φmax-最大填球角。
轴承滚球个数z一般为基数,根据公式(1)和等截面四点接触球轴承结构参数,本文选择滚球个数z为45。
当轴向力单独作用在等截面四点接触球轴承滚球与滚道时,各滚球受载相同,如图2(a)所示,每个滚球与滚道的接触载荷Pa为:
(2)
在圆周上径向力对滚动体产生最大接触载荷Q0的角度位置设为φ0=0,如图2(b)所示。处于φ角度位置滚球承受径向接触载荷可表示为:
Fr=[Q0+2∑(Pφcosφ)]·cosα,其中φ≤π/2
(3)
处于φ角度位置滚柱承受径向接触载荷可表示为:
Fr=Q0+2∑(Qφcosφ),其中φ≤π/2
(4)
(5)
(6)
滚球径向载荷表示为:
(7)
当倾覆力矩单独作用在等截面四点接触球轴承滚球与滚道时,如图2(c)所示,忽略接触角影响,假定接触变形只发生在滚球的竖直方向。倾覆力矩单独作用下滚动体竖直方向最大变形量为δmax,则δφ=δmaxcosφ,正压力的竖直分量对Y坐标产生的力矩为:
(8)
(9)
在角度φ处单位弧长上的载荷PM为:
(10)
当等截面四点接触球轴承同时承受轴向力和倾覆力矩作用时,运用载荷叠加法获得等截面四点接触球轴承滚球与滚道受载后最大接触载荷Qmax为[11]:
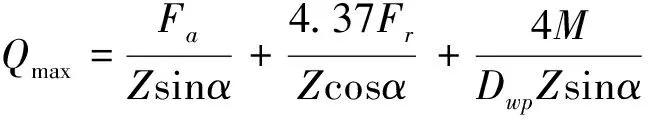
(11)
根据表1中等截面四点接触球轴承结构参数及公式(11),获得滚球与滚道最大接触载荷为1769 N,后续将用于滚球与滚道局部有限元模型中。
1.2 等截面四点接触球轴承承载能力理论计算
轴承求解力学性能的经典方法是赫兹接触理论,赫兹接触理论做了以下假设:滚球垂直作用于滚道,接触区域仅发生弹性变形,忽略滚球与滚道间摩擦[12-14]。赫兹接触理论计算滚球与滚道接触长短半轴和最大接触应力如下[15-16]:
(12)
(13)
(14)
式中:a-接触区域长半轴长,a*-赫兹接触系数,b-接触区域短半轴长,b*-赫兹接触系数,E-弹性模量,Q-接触载荷,u-泊松比,∑ρ-曲率和。
根据表1中等截面四点接触球轴承结构参数及式(11)、式(12)、式(13)和式(14),查《球轴承的设计计算》[17]表获得滚球与滚道最大接触应力为4005.2 MPa,接触区域长半轴长0.58306 mm,短半轴长0.36187 mm。
2 等截面四点接触球轴承局部承载能力数值计算
2.1 等截面四点接触球轴承数值模型验证
为了验证等截面四点接触球轴承有限元模型精度,在保证模型计算精度的情况下减少有限元模型的网格数量,选取1/4滚球和滚道模型,如图3所示,截取部分滚球和滚道。滚道底面约束全部自由度,滚球保留X方向平移自由度和Y方向平移自由度,其他自由度被约束。在实际工况中,当等截面四点接触球轴承受载后,滚球往滚道边缘移动,接触角发生变化,滚球上的载荷不垂直于滚道,不满足赫兹接触理论中载荷垂直施加在接触表面的假设,因此,赫兹接触理论不能直接验证等截面四点接触球轴承局部接触有限元模型的计算结果。为了解决上述问题,在滚球上施加与初始接触角方向相同的载荷F,保证滚球与滚道之间始终垂直接触,如图4所示,这样等截面四点接触球轴承局部接触有限元模型满足赫兹接触理论假设,验证滚球与滚道局部接触有限元模型的有效性。
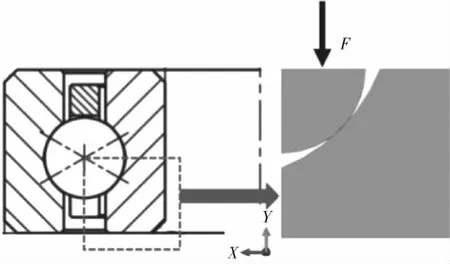
图3 滚球与滚道接触局部有限元模型
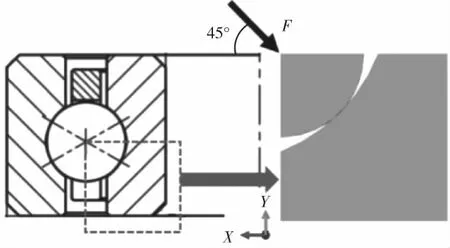
图4 滚球与滚道接触局部有限元验证模型
为了验证滚球与滚道接触局部有限元模型的有效性,对赫兹接触理论计算结果和滚球与滚道接触局部有限元验证模型结果进行对比,以赫兹接触理论为基准,采用图4中载荷施加方式,使滚球载荷垂直于滚道,满足赫兹接触理论假设。选择滚球与滚道接触区域的不同有限元网格尺寸,MS 0.04(网格尺寸0.04 mm)、MS 0.06(网格尺寸0.06 mm)、MS 0.08(网格尺寸0.08 mm)、MS 0.10(网格尺寸0.10 mm)、MS 0.12(网格尺寸0.12 mm)。如图5(a)所示,当有限元网格尺寸由大变小过程中,滚道上的等效应力逐渐变大。如图5(b)所示,当有限元网格尺寸由大变小过程中,最大接触应力的波动由剧烈变平缓,与赫兹接触理论获得的最大接触应力值误差逐渐变小,当有限元网格尺寸为0.04 mm模型的误差为3.201%。如图5(c)所示,对比接触区域面积,当有限元网格尺寸为0.04 mm模型的误差为5.702%,误差在可接受范围[18],有限元模型中网格尺寸为0.04 mm时对有限元计算结果的影响较小,所以最终滚球与滚道接触区域有限元网格尺寸为0.04 mm,用于后续承载能力分析,选取有限元网格尺寸大小与王大力等[19]和Satyanarayana等[20]的研究分析相吻合。
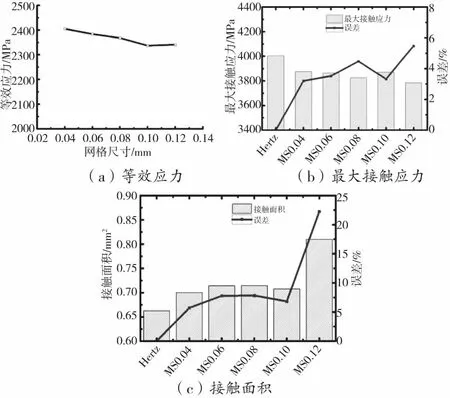
图5 滚球与滚道接触局部有限元验证模型结果
2.2 等截面四点接触球轴承局部承载能力数值计算
当等截面四点接触球轴承正常工作时,滚球与滚道载荷施加形式如图3所示。如图6(a)所示,滚球与滚道局部接触区域的最大等效应力为2133 MPa,最大等效应力位置位于滚球与滚道接触区域的表面下方。如图6(b)所示,在滚球与滚道接触有限元模型中,滚道表面接触应力最大值为3443 MPa,接触区域形状类似于椭圆形,而在2.2节中,通过赫兹接触理论计算的滚球与滚道最大接触应力为4005.2 MPa,两者误差为14.04%。影响等截面四点接触球轴承承载性能的重要参数之一是接触角,从滚道圆弧中点到滚道最大等效应力点连线,与水平夹角为接触角,当空载时滚道与滚动体之间属于点接触,随着载荷的增加,滚道与滚球接触区域变为面接触时,等效应力最大的地方发生变化。如图6(c)所示,滚球与滚道接触模型受载后接触角为45.52°,与初始接触角45°不同,所以,对于等截面四点接触球轴承不满足赫兹接触理论假设,不能直接通过赫兹接触理论对数值模型进行验证。
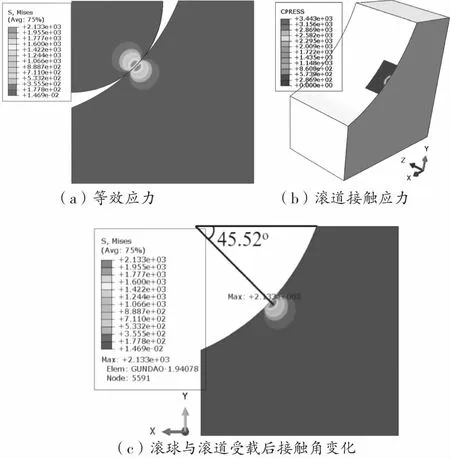
图6 滚球与滚道接触局部有限元模型结果
3 等截面四点接触球轴承整体承载能力数值分析
3.1 等截面四点接触球轴承整体有限元
等截面四点接触球轴承尺寸大,滚动体数目多,整体有限元模型不仅花费大量建模时间,而且计算时间长,接触对数量多,计算收敛难度大,对计算设备要求高。使用非线性结构代替滚动体,模拟滚道与滚球之间的接触行为,可大幅缩小等截面四点接触球轴承有限元模型的规模和计算时间,降低计算难度。根据赫兹接触理论,等截面四点接触球轴承中滚球与滚道载荷-变形可描述为:
(15)
式中:K-刚度系数,Q-接触载荷,δ-变形量。
K的数值由等截面四点接触球轴承滚道直径、滚球直径、滚道曲率半径和材料特性确定,根据参考文献[17]所提供的计算方法以及相关参数,K取值446961 N/mm。根据图1和表1的结构和参数在ABAQUS/CAE中建立等截面四点接触球轴承数值模型。采用Partition功能菜单,对内外圈进行分区切割,滚道上网格尺寸为0.05 mm,单元形状为Hex六面体单元,结构化网格,网格划分算法为Medial Axis中性轴算法,单元类型选择C3D8I,如图7(a)所示。等截面四点接触球轴承内圈全固定,外圈上表面与参考点RP-1运动耦合(Kinematic coupling),约束X轴和Y轴方向的移动及X轴和Y轴方向的转动,表1中的载荷施加在参考点RP-1,如图7(b)所示。在Interaction接触功能模块中,弹簧/阻尼器菜单中选取两点连接方式创建线性弹簧,弹簧的连接端点对应滚球与滚道的接触点,利用非线性弹簧代替滚球,两对非线性弹簧表示一个滚球,如图7(c)所示。
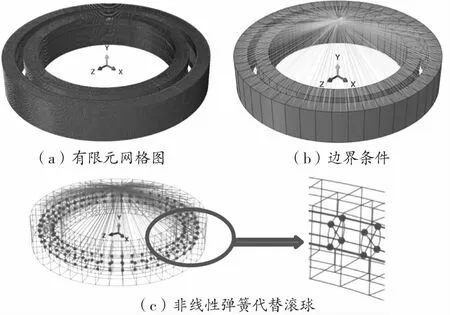
图7 等截面四点接触球轴承整体有限元模型结果
3.2 等截面四点接触球轴承整体承载能力数值计算
将图2(b)中角度φ根据滚球个数等分获得不同滚球所处位置,代入公式(3)获得各滚球所受的倾覆力矩,与公式(2)轴向力叠加,获得每个滚球所受的载荷,如图8所示。这个结果为解析结果,内外圈假设为刚体,仅滚球与滚道接触区域发生变形。提取等截面四点接触球轴承整体有限元模型中弹簧上的载荷,获得各滚球所受载荷。滚球受压,所以载荷为负值。如图8所示,等截面四点接触球轴承解析结果和数值结果的载荷分布趋势相同,数值结果大于解析结果,这是由于数值模型中的内外圈为弹性体,受载后发生变形。如表2所示,如果以解析结果为基础,数值结果对比的误差为15%,在允许误差范围内[18]。等截面四点接触球轴承整体有限元模型变形如图9所示,在内圈固定的情况下,载荷施加在外圈上端面,所以变形发生在外圈。根据公式(2)和公式(3)及表1的数据可知,各滚子所受的轴向力远大于倾覆力矩,所以外圈各处未出现明显扭转。

表2 各模型求解最大接触载荷对比
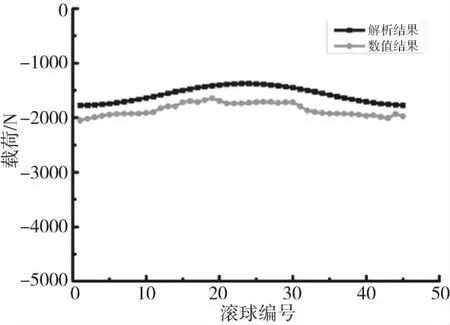
图8 等截面四点接触球轴承整体有限元模型结果与解析结果对比

图9 等截面四点接触球轴承整体有限元模型变形图
等截面四点接触球轴承结构尺寸大,套圈的抗变形能力不易保证,部分学者认为许用接触应力应取低一些,国际上轴承厂家基本上取万分之一滚动体直径变形时的接触应力为最大接触应力,ISO国际标准和ANSI美国国家标准[21]给出不同类型轴承滚动体直径万分之一永久变形的接触应力,点接触形式最大接触应力为4200 MPa。滚道静承载能力以滚动体允许的最大变形时接触应力与许用接触应力的比值来衡量,因此,用静态安全系数来衡量等截面四点接触球轴承滚道静承载能力。等截面四点接触球轴承安全系数计算公式为:
(16)
式中:fs-安全系数,σmax-滚球与滚道接触应力,[σmax]-滚球与滚道许用接触应力。
等截面四点接触球轴承静载荷安全系数fs一般大于1.5,根据滚球与滚道接触强度的安全系数为1.82,说明在最大载荷条件下,其强度可以保证等截面四点接触球轴承主机的使用性能要求。
4 结论
本文通过对等截面四点接触球轴承承载能力进行分析,建立接触滚球与滚道有限元验证模型,与赫兹接触理论通过最大接触应力和接触面积对比分析,运用验证过的滚球与滚道接触有限元模型进行承载能力分析,结论如下:轴承局部接触有限元模型中,大尺寸有限元网格尺寸模型计算结果远远大于小尺寸有限元网格模型,对等截面四点接触球轴承承载能力分析影响大。在等截面四点接触球轴承正常工况时,由于滚球与滚道之间接触角发生较大变化,不满足赫兹接触理论中载荷垂直施加在滚道上的假设,不能用于局部接触有限元结果验证。等截面四点接触球轴承整体数值模型内外圈设置为弹性体,所以计算结果大于解析结果。通过对等截面四点接触球轴承承载能力的研究,一方面提高等截面四点接触球轴承承载能力的计算精度和有效性,另一方面有利于降低等截面四点接触球轴承有限元模型的规模,提高等截面四点接触球轴承计算分析的效率,为等截面四点接触球轴承设计人员计算校核承载能力和结构优化设计提供重要参考。
