基于CCD 的立式五轴机床滑枕多目标优化*
2023-11-15王松明廖映华廖鑫宇
王松明 廖映华 李 磊 廖鑫宇 李 坤
(四川轻化工大学机械工程学院,四川 宜宾 644002)
滑枕是立式五轴机床的关键运动部件,其静动态特性对整机的加工精度及平顺性有重要影响[1]。在工作过程中,滑枕运动到低点时,与轴承座形成竖向的悬臂结构,在切削力作用下易发生共振变形。因此,提高滑枕静动态特性有利于提高立式五轴机床的加工精度和生产效率。
近年来,随着精密制造的迅速发展,对立式五轴机床的加工精度提出了更高的要求。为了进一步提高其加工质量,国内外学者对机床的核心部件进行优化研究。刘成颖等以立柱为研究对象结合拓扑优化,并选择W 型筋板对立柱优化[2],有效地改善了整机的动态性能;邱自学等运用模糊综合评价方法实现滑枕改进方案优选,有效提高了滑枕的静动态特性[3];谢军等利用拓扑优化方法对主轴箱结构进行了改进,减少了主轴箱的变形并实现轻量化[4];张国辉等利用灵敏度分析对横梁进行多目标优化,提高了横梁的静动态特性[5];Qian Y 等根据机床主轴在不同工况下结合灵敏度分析对主轴进行多目标优化[6]。
以上研究在结构优化方面均取得了一定成效,但大多数研究是对原结构优化改进,忽视了其他结构方案的优选型。考虑到滑枕结构设计变量的复杂性及评价指标的多样性,以往研究并没有对滑枕具体筋板方案及相关尺寸进行优化。为此,本文以某型号五轴立式机床的滑枕为研究对象,提出一种筋板布置与响应面法相结合的多目标优化设计方法。在原滑枕结构基础上,设计出5 种不同内部筋板布置结构,逐一建立滑枕的参数化模型和有限元模型,分别对其进行静力学和模态分析。以总变形量、1阶固有频率和质量作为评价指标,对有限元仿真数据综合对比选出井型结构作为优选方案,利用灵敏度分析得出敏感尺寸进行中心组合设计,结合响应面优化,最后进行多目标遗传算法(multi-objective genetic algorithm,MOGA)优化,优化流程如图1 所示。
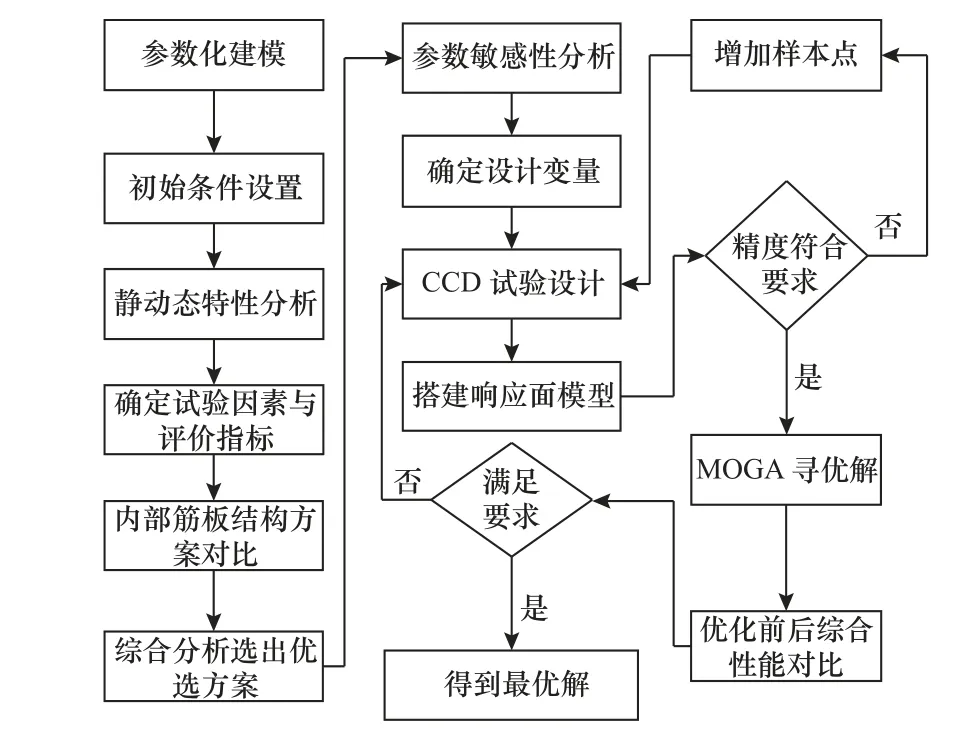
图1 滑枕分析与优化流程
1 滑枕结构有限元分析
1.1 立式五轴机床结构分析
某型号立式五轴机床(图2)主要包括床身、A/C转轴、直线导轨、横梁、十字滑座、滑枕、工作台等零部件。在加工时,十字滑座沿着横梁做X轴运动,横梁沿前后方向在直线导轨上做Y轴运动,滑枕通过滑块嵌入十字滑座中沿竖向做Z轴运动。精密高速主轴安装在滑枕下端,通过主轴上安装的刀具来对固定在工作台上的零件进行高速铣削加工。滑枕是立式五轴机床的核心移动件,其静动态性能直接关系到整机的加工精度。

图2 立式五轴机床结构图
1.2 滑枕结构有限元分析模型的建立
根据立式五轴机床滑枕组件的实际结构情况,在SolidWorks 绘制参数化模型并导入Ansys Workbench,对滑枕添加实际材料属性。采用灰铸铁HT300 整体铸造,材料属性设置见表1。同时,考虑到滑枕内部结构较为复杂,为提高软件计算效率,根据圣维南原理,对模型的部分特征进行了合理的简化,压缩了一些对模拟仿真结果影响较小的细微特征[7]。

表1 材料主要属性设置
根据滑枕的结构特点,为了满足计算精度,将网格单元尺寸更改为10 mm,采用自由网格划分。在进行网格划分时,还需对网格进行校核,以免解得的数值结果产生过大的误差。在对滑枕进行了网格划分后,滑枕有限元网格划分模型如图3a 所示。模型的节点数为160 497,单元数为92 654。

图3 滑枕结构有限元分析
1.3 边界条件的设定
有限元分析前处理还需要给模型添加载荷及约束,参考滑枕实际的装配构造,对轴承座安装位置施加固定约束,对滑块导轨位置施加无摩擦支撑。在载荷条件的施加中,应考虑滑枕运动到最低点时,是受力最恶劣的工况。滑枕受到铣削加工刀具前端传来的主切削力Fc、绕主轴方向的扭矩T及自身重力G1,还受到安装在滑枕上附属配件重力G2作用,其受力分析简图如图3b 所示。经过查验立式五轴机床操作手册确定具体工况参数为被加工面宽150 mm,每齿进给量0.25 mm,切削深度1.2 mm,铣刀直径13 mm,铣刀转速2 200 r/min。滑枕所受到的铣削力可由经验公式[8](1)计算得出。
式中:Fc为主切削力;ae为加工宽度;ap为切削深度;fz为每齿进给量;z为刀具齿数;n为刀具转速;d为刀具直径;Fx为横向进给力;Fy为纵向进给力;Fz为垂向进给力。将各参数带值计算,最终载荷见表2。

表2 载荷参数取值
1.4 静力学分析
在上述端铣工况下,对滑枕静力学特性仿真求解,得到滑枕的综合变形云图如图4a 所示,滑枕的最大总变形量为0.209 89 mm,发生在滑枕的下方端口部位;图4b 所示为滑枕的等效应力分布云图,滑枕的最大应力为54.599 MPa,小于灰铸铁材料的许用应力335 MPa。由于滑枕引起的变形较大,对整个机床的加工精度有很大的影响,因此,为减小整体的变形,还需要对滑枕结构优化。

图4 滑枕静力学分析结果
1.5 滑枕模态分析
为了明确滑枕结构的振动特性,需要进行模态分析,来判断其是否与外界激励的频率相近,进而预测其是否发生共振。由振动理论可知[9],低阶固有频率对机械结构的动态特性影响贡献最大,为此,采用Block-Lanczos 方法,提取了滑枕的前6 阶固有频率和它的振型特点(表3),可知滑枕的1 阶固有频率为85.115 Hz,其1 阶模态云图如图5 所示。

表3 前6 阶模态固有频率及振型的结果

图5 滑枕1 阶模态云图
当主轴高速运转时会对滑枕产生激励作用,电机对滑枕激振频率计算公式[10]为
式中:f为激振频率;δ为浮动误差,一般数值取50;n为电机转速,最高转速nmax=2 200 r/min,将以上工作参数代入式(2)可求得fmax=75 Hz。滑枕的1 阶固有频率为85.115 Hz,与最大激振频率fmax比较接近,容易与主轴形成共振,会影响机床稳定性。因此,为进一步提高立式五轴机床的加工精度,需要提高滑枕的1 阶固有频率。
2 滑枕结构方案的改进与优选
滑枕内部筋板尺寸结构和布置方案对滑枕的各项性能有着重要的影响,基于原滑枕结构筋板布置,设计出井型、米型、蜂型、菱型和X 型5 种改进方案,在SolidWorks 中分别建立三维参数化模型,其内部半剖视图如图6 所示。
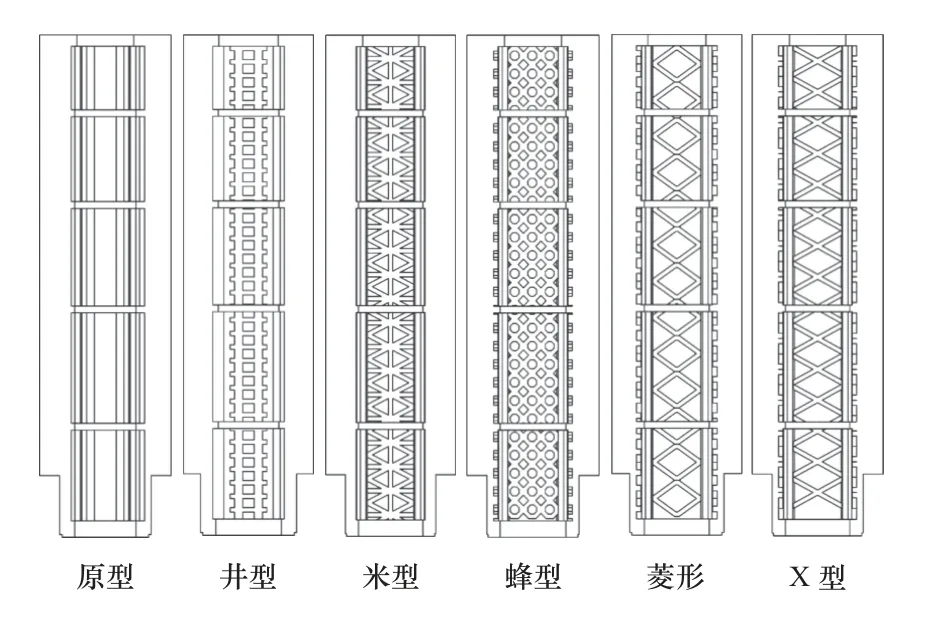
图6 滑枕内部筋板结构
为了准确、全面地反映各个方案滑枕结构的性能优劣,以1 阶固有频率衡量滑枕的动态性能;选择最大变形量作为评价指标反映滑枕的静力学性能;选择质量作为评价指标反映滑枕的轻量化水平。根据设计的5 种滑枕结构方案,逐一建立相对应的滑枕有限元模型,并进行仿真分析,各个方案滑枕有限元分析结果见表4。
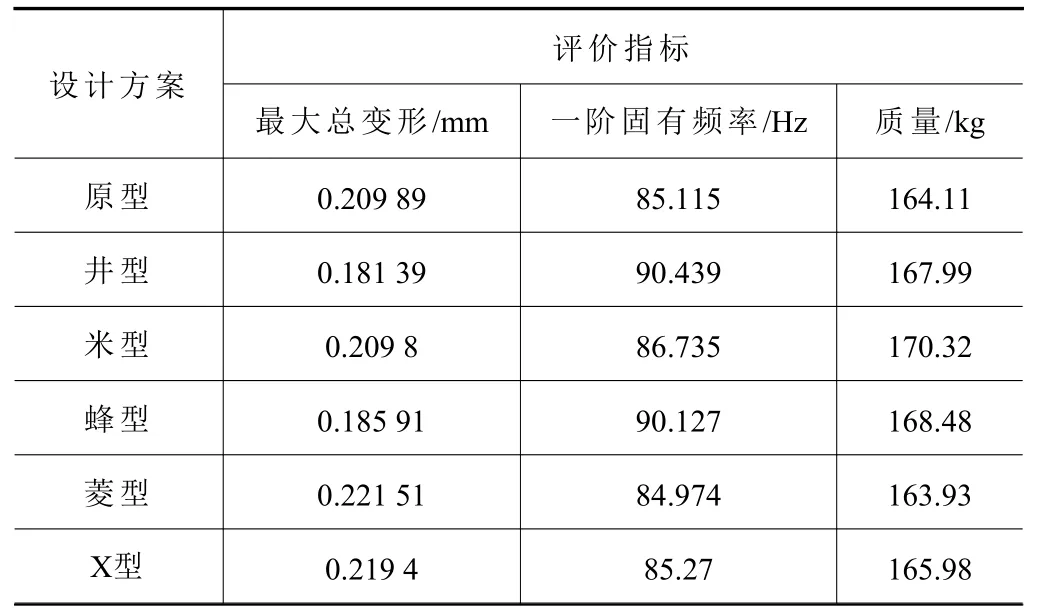
表4 各方案滑枕静动态性能仿真分析结果
由表4 各方案滑枕静动态性能仿真分析结果可知,在质量相近的情况下,井型结构的总变形最小为0.181 39 mm,同时其1 阶固有频率最大为90.439 Hz,符合优选条件,因此选取井型结构进行多目标优化。
3 滑枕结构的响应面优化设计
3.1 灵敏度分析
滑枕在结构框架一定时,其尺寸灵敏度的数值能够体现各个参数对结构性能的影响程度。为满足实际工况的使用要求,以减小滑枕的总变形量、提高1 阶固有频率为目标,对关键尺寸参数进行优选,可以提高后续优化计算效率。选取各个设计变量如图7 所示。
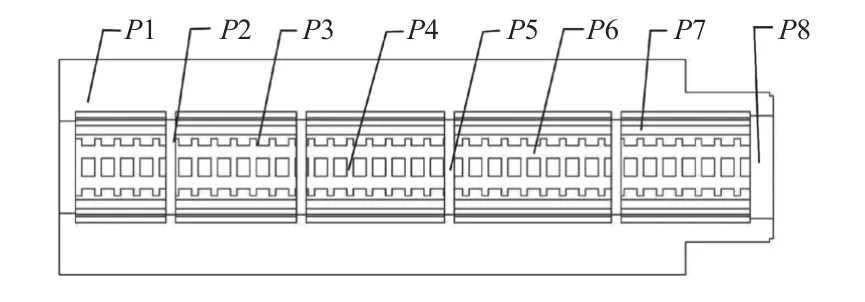
图7 滑枕设计变量与取值范围
根据图5 所示的滑枕半剖结构简图,选取壁厚P1、筋圆半径P2、横筋长P3、筋间距P4、圆筋板厚度P5、筋长P6、筋宽P7、端口厚度P8 等8 个关键尺寸作为设计变量。表5 列出了各个参数代号、初始值和对应的变化范围。
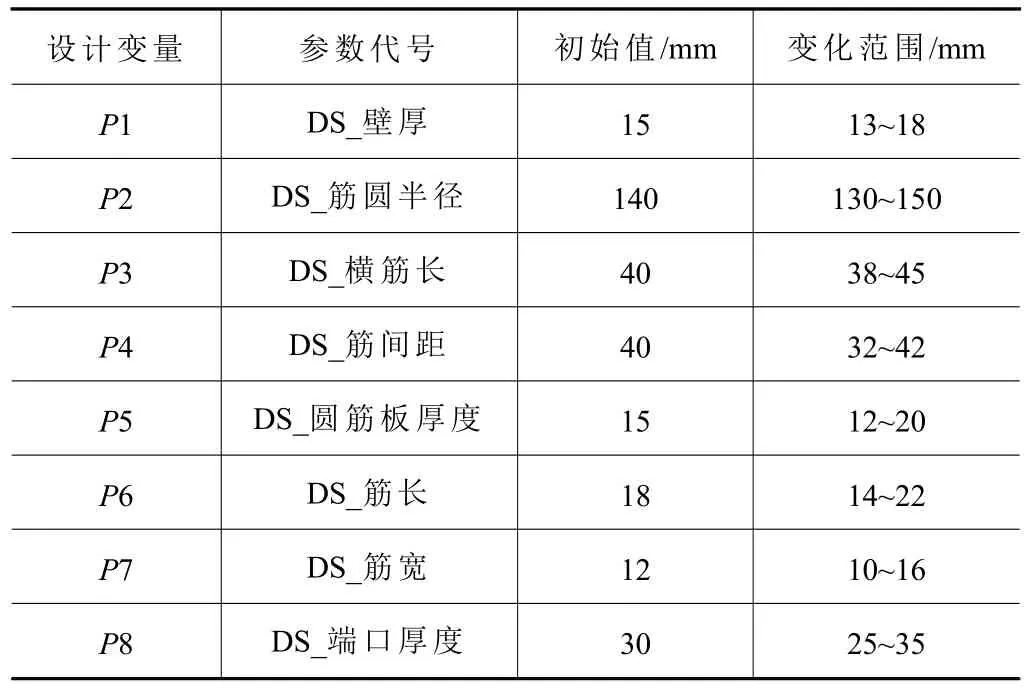
表5 滑枕设计变量与取值范围
进行参数灵敏度分析,首先在Geometry 中选择拟定的设计变量,再选取质量、最大总变形量和1 阶固有频率作为输出量,在Parameters set 可以改变取值范围,采用Spearman 方法对各参数间的关系进行分析,建立了灵敏度矩阵,以表达输入量和输出量之间的相关敏感性。从数学角度上,灵敏度是对函数求偏导,得出各个设计变量对评价指标的贡献值,灵敏度函数可表示为[11]
完成对滑枕的尺寸参数灵敏度分析(图8):P1、P6、P7 对1 阶固有频率和质量的正相关灵敏度较大,P1、P6、P7 对最大总变形量负相关灵敏度较大,其他参数灵敏度绝对值不超过0.2 可忽略。由此,后续选取P1、P6、P7 这3 个尺寸参数作为滑枕结构关键尺寸进行优化。
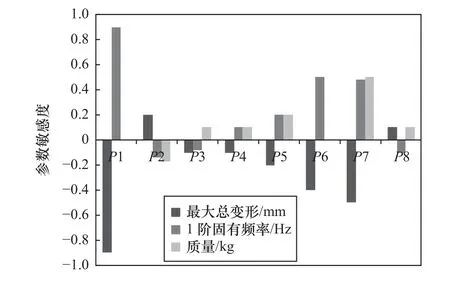
图8 参数灵敏度分析
3.2 试验设计
文中采用中心组合设计方法来自动划分并选取设计点,CCD 由分部试验设计演变而来[12],选取P1、P6、P7 这3 个尺寸参数作为设计变量,得到15 组不同实验方案,具体样本数据及试验结果见表6。
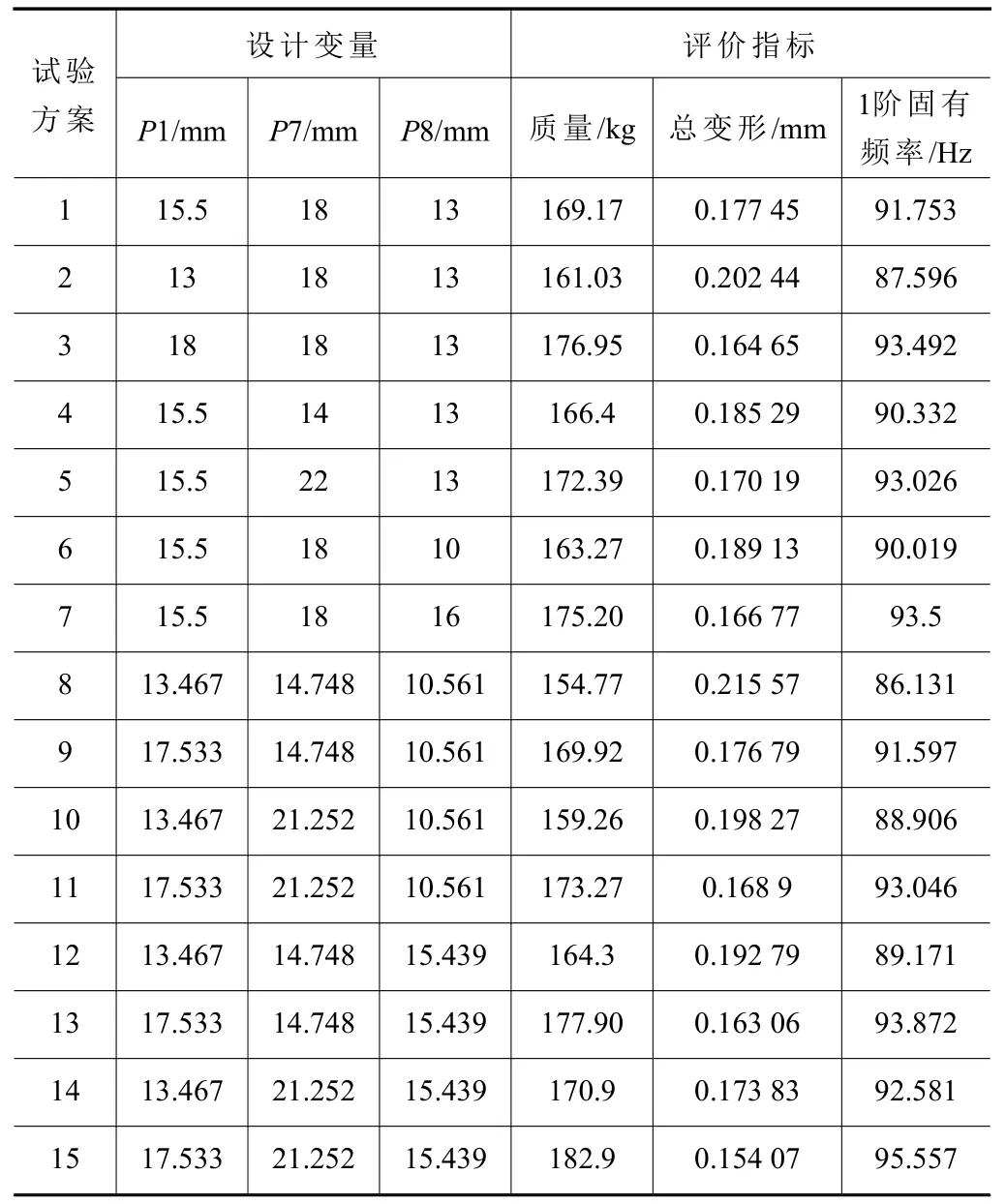
表6 CCD 试验样本设计
3.3 响应面法分析
响应面法通过合理的试验方法对所得设计点进行试验,得设计变量对目标函数的响应值并构造响应面[13],将其运用到有限元分析中。通常响应面模型采用二次多项式,对于m个变量,响应面模型y(x)为
式中:X为设计变量向量;xi为设计变量;C0、Ci、Cii、Cij为未知系数,其个数N=(m+1)(m+2)/2。
基于收集的样点数据,采用多目标遗传算法建立响应曲面的模型[14]。图9 是响应面拟合优度图,可见,总变形量、1 阶固有频率及质量的样本点均位于y=x函数图像附近,表明设计样本点与响应面吻合程度高。
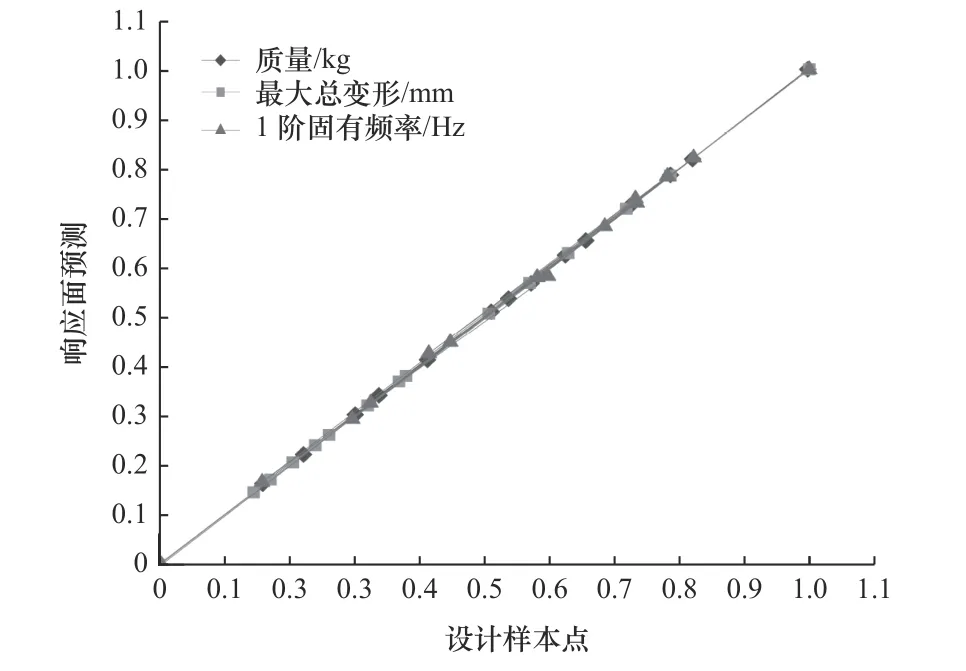
图9 响应面拟合优度图
图10 所示为P1、P6、P7 与它们的模型特性之间的响应面曲线,可以看出,滑枕的设计变量与1阶固有频率呈非线性关系(图10a),与总变形量和质量近似为线性关系(图10b 和图10c)。

图10 响应面模型
3.4 基于多目标优化求解
文中采用多目标遗传算法,由非支配排序遗传算法Ⅱ推演而来[15]。为寻找全局最优解,必须预先设置目标函数、设计变量和约束条件。以滑枕总变形量最小、1 阶固有频率最大及质量最小作为优化的3 个目标,该多目标优化数学模型可表示为
式中:pi为设计变量,i=1,2,3;m(pi)为滑枕的质量函数;σ(pi)为最大变形量函数;f(pi)为1 阶固有频率函数。多目标遗传算法的设置参数见表7。

表7 MOGA 的参数设置
通过MOGA 优化后,可以得到滑枕参数帕累托最优解。由于设计变量取值是在自上而下的设计过程中关联得到的,尺寸不成整数,为了便于实际生产,需要对优化尺寸进行圆整,其圆整结果见表8。

表8 设计变量圆整结果
3.5 优化结果分析验证
重新建立滑枕有限元模型并进行仿真,由优化后滑枕的变形云图(图11a)与1 阶模态振型云图(图11b)可知,最大总变形量为0.161 1 mm,1 阶固有频率为94.385 Hz。

图11 优化后滑枕的变形云图与1 阶模态振型云图
滑枕优化前后的评价指标对比结果见表9。通过对滑枕井型结构方案的多目标优化,在滑枕总质量仅增加3.32%的情况下,其最大总变形减小23.25%,一阶固有频率增加10.89%,证实了该优化方案的可靠性。
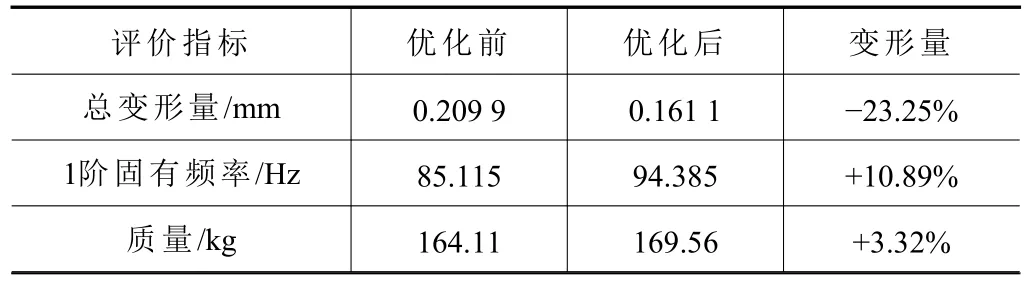
表9 滑枕优化前、后评价指标对比
4 结语
(1)本文在滑枕筋板布置优选方案基础上,提出了一种基于CCD 的响应面法与多目标优化相结合的方法,根据原滑枕结构,设计出5 种不同筋板结构布置,设立方案评价指标,逐一进行静力学分析和模态分析,根据质量、最大总变形量和1 阶固有频率3 个评价指标综合比对分析,选出井型结构作为最佳方案。
(2)对井型结构尺寸参数进行灵敏度分析选出关键尺寸,利用多目标遗传算法取最优参数解。优化结果表明:与原结构相比,在总质量增加3.32%的情况下,其最大总变形减小23.25%,1 阶固有频率增加10.89%,取得良好的优化效果。同时也验证了该优化方法的合理可靠。
