试验台支承对滑动轴承动特性系数识别精度的影响研究＊

2023-11-15陈润霖崔亚辉

制造技术与机床 2023年11期

徐帆唐杰陈润霖杜辰崔亚辉刘凯

（西安理工大学机械与精密仪器工程学院，陕西西安 710048）

滑动轴承被广泛应用于多个工业领域，具有承载力大、稳定性好等优点[1-2]，目前已经具备了较为完整的理论体系[3-5]。但是随着旋转机械设备的性能提升，对滑动轴承的动特性提出了更高要求，通过试验获取轴承动特性变得尤为重要[6]，但是动特性测试过程容易受到各种因素的干扰，从而引入测试误差，导致最终识别的动特性系数与真实值相差甚远[7]。

滑动轴承的动特性识别就是通过测试手段获取轴承的刚度阻尼系数，常用的方法包括脉冲激振识别法[8]、锤击法[9]、正弦激振法[10]和多频激振法[11]等。Wang L 等[12]采用非接触式谐波激励法和附加不平衡激励法分别进行了高速水润滑动静压轴承的动特性系数的识别，并将实验结果和理论预测进行了对比。袁小阳等[13]用多频技术来识别油膜的动特性系数，提出了振动响应或固有频率评价法和轴承系统失稳评价法。王永亮等[14]根据轴颈扰动与非线性油膜力的关系，利用等幅异频位移激励技术识别油膜的动特性系数。马石磊等[15]设计和搭建了一种轴承转子系统实验台，用不平衡质量法识别轴承的动特性系数。

这些测试结果与理论值都存在一定的误差，大多未考虑滑动轴承动特性测试过程中由于外界干扰引入的误差，包括测试仪器系统误差、数据处理误差等[7-16]。Wu Q Y 等[17]提出了一种新型磁悬浮动态标定方法，利用力和位移的双通道联合标定，能够在一定程度上减小测试仪器带来的误差，避免静态标定的不足[18-19]，但是仍然无法完全消除测试系统中其他元件和连接产生的误差[20-21]。这样，残余误差对动特性系数的识别精度仍然有影响，且影响程度与动特性试验台本身的参数有关[22]。

本文针对滑动轴承倒置式试验台，采用仿真方法模拟轴承动特性测试过程，重点分析试验台支承刚度和支承阻尼的大小对轴承动特性系数识别精度的影响，为滑动轴承动特性试验台建设和测试参数选取提供必要的数据支持。

1 滑动轴承倒置式试验台方案及动特性识别方法

1.1 试验台及测试方案

滑动轴承倒置式试验台方案如图1 所示，转子在驱动力的作用下旋转。除润滑系统和驱动系统等辅助系统外，试验台主体部分主要由试验轴承系统、静载系统、动载系统和支承系统组成。试验轴承为滑动轴承，该系统的支撑装置主要是滚动轴承。

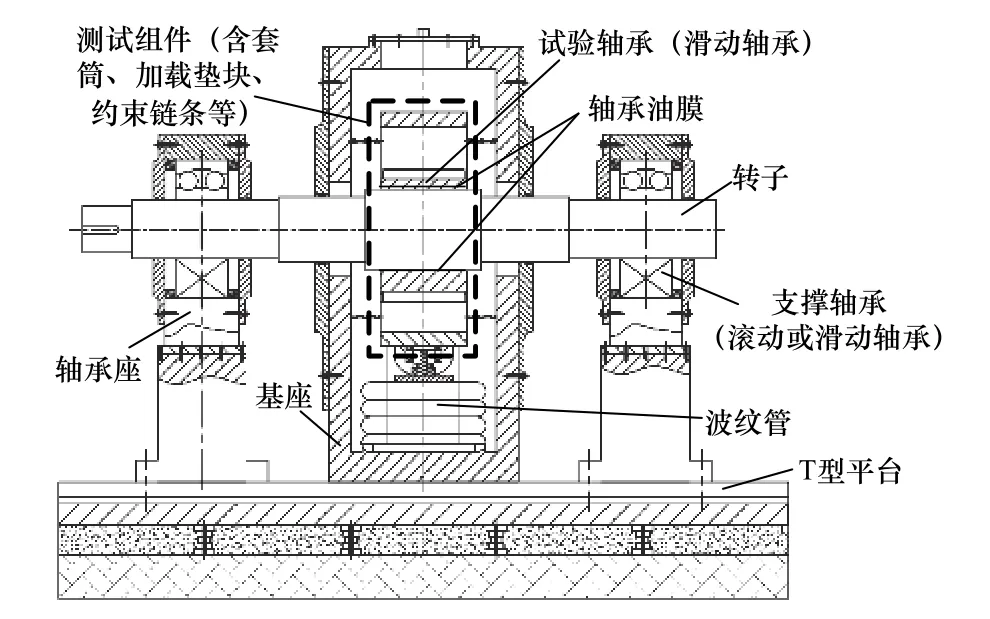
图1 倒置式轴承动特性试验台方案

1.2 动特性识别方法

在考虑系统的连接刚度和连接阻尼的情况下，该试验台系统的动力学模型如图2 所示，以单频两次激振法为例，假设所施加的激振力矢量通过轴承的几何中心，且轴承作平面平行运动。(X01,Y01)为激振力F1作用下试验轴承相对于静平衡位置的绝对位移；(X11,Y11)为试验轴承处转子的绝对位移；(X21,Y21)为试验轴承轴孔中心相对转子轴心的位移。(X02,Y02)为激振力F2作用下试验轴承相对于静平衡位置的绝对位移；(X12,Y12)为试验轴承处转子的绝对位移；(X22,Y22)为试验轴承轴孔中心相对转子轴心的位移。其中，试验轴承轴孔中心相对转子轴心的位移与试验轴承处转子的绝对位移之和为试验轴承相对于静平衡位置的绝对位移，由此，可以消掉公式中的(X11,Y11)和(X12,Y12)。

图2 倒置式试验台的动力学模型

当只有F1作为激振力时，可得到试验台系统的运动微分方程，见式（1）。

当只有F2作为激振力时，可得到试验台系统的运动微分方程，见式（2）。

式中：F1和F2为激振力；m、m1分别为试验轴承和转子质量；k、c为试验轴承的刚度阻尼系数矩阵；k0、c0为试验台连接刚度阻尼系数矩阵；k1、c1为转子支承的刚度阻尼系数矩阵。

考虑到方程的独立性，对式（1）和式（2）均取第一个微分方程进行傅里叶变换，然后整理得到滑动轴承动特性系数测量方程（3）。

式（3）即为滑动轴承动特性系数测量方程，方程左边即为待求参数k、c，方程右端为测试过程中获得的激振力和位移信号，然后对已经获得的激振力和位移信号进行傅里叶变换，得到幅值和相位，利用幅值和相位数据计算F、X的实部和虚部，代入式（3），令其实部和虚部分别对应相等，可得到8 个线性方程，从而求解出滑动轴承的8 个动特性系数，完成动特性系数的识别。

2 滑动轴承动特性系数的识别精度仿真评估方法

滑动轴承的动特性识别是根据试验台的激振力和振动响应来反求轴承的动特性系数，本文根据试验台系统的正反动力学问题，提出滑动轴承动特性系数识别精度的仿真评估方法，如图3 所示。首先已知试验台系统的激振力及油膜刚度阻尼矩阵k、c，可以求解出在激振力F1和F2作用下轴承相对于平衡位置的相对振动响应及相对于转子轴心的绝对振动响应，其中F1作用下轴承相对振动的幅值和相位分别为Ax21、Ay21和φx21、φy21，绝对振动的幅值和相位分别为Ax01、Ay01和φx01、φy01；F2作用下相对振动的幅值和相位分别为Ax22、Ay22和φx22、φy22，绝对振动的幅值和相位分别为Ax02、Ay02和φx02、φy02。

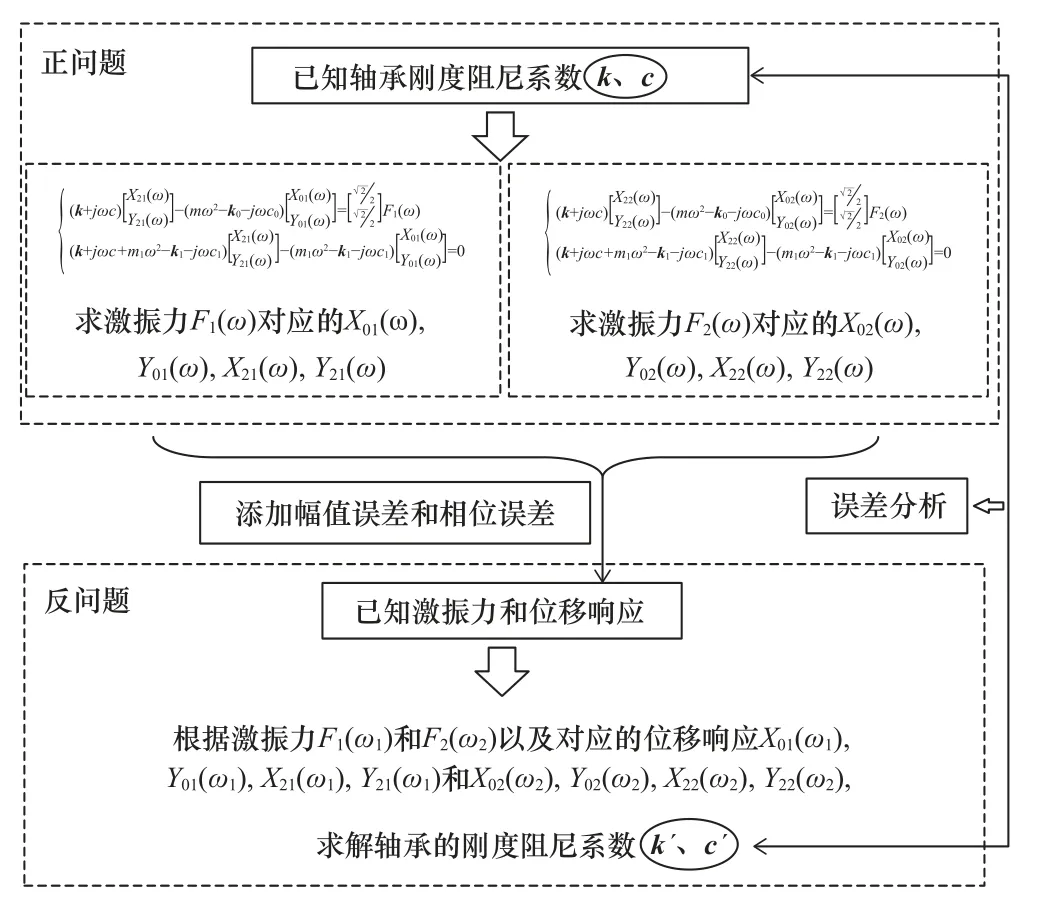
图3 基于正反动力学问题的动特性系数识别精度评估方法

在实际测试过程中，由于测试仪器硬件和环境的干扰，测试获取的信号与真实信号之间存在误差，这种测试误差主要包括幅值误差和相位误差，将测试误差直接添加到仿真得到的位移数据中，用于模拟真实振动测试数据，即：

式中：Am0、Am为添加误差前后信号的幅值；φ、φ0为添加误差前后信号的相位；aA、aφ分别为幅值的相对误差和相位的绝对误差。

根据动特性识别的求解算法，将添加测试误差的振动信号作为输入，可识别出轴承的刚度阻尼系数矩阵k′、c′，将其与试验台轴承的刚度阻尼的设定值k、c进行对比，可评估轴承动特性系数的识别精度为

式中：εk为刚度系数识别误差；εc为阻尼系数识别误差。

3 试验台支承对轴承动特性系数识别精度的影响分析

3.1 试验台参数

本文所研究的滑动轴承倒置式试验台系统参数见表1，根据一般滑动轴承动特性测试的实际情况，设置测试过程中存在+5%的幅值误差和+1º的相位误差[18]。

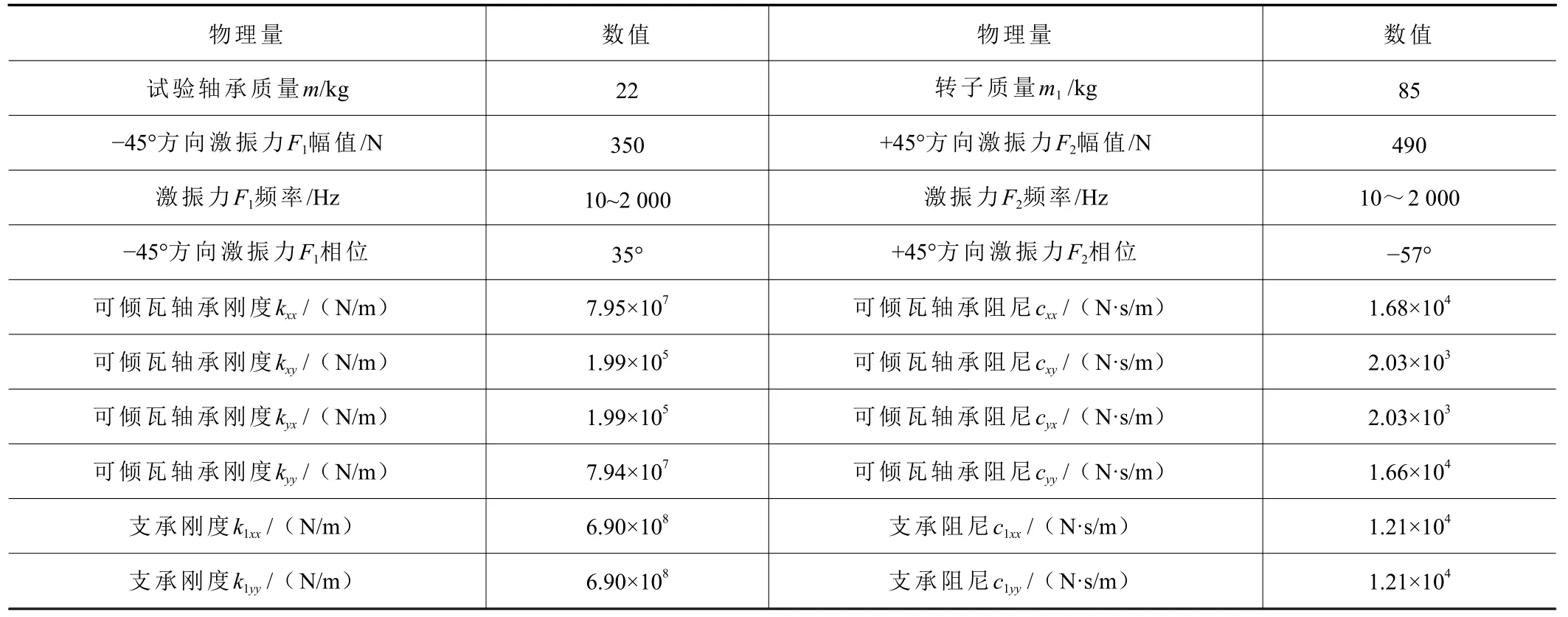
表1 倒置式轴承动特性试验台的参数

3.2 支承刚度的影响分析

试验轴承的主刚度为kxx，主阻尼为cxx，当试验台支承刚度为表1 中初值的0.001～1 000 倍时，在激振频率为0～1 000 Hz 时，试验台支承刚度对轴承动特性系数的影响规律分别如图4 和图5 所示。为方便分析，将图分为A、B、C、D 这4 个部分，分别代表不同频率和不同支承刚度时对应的主刚度和主阻尼识别误差。

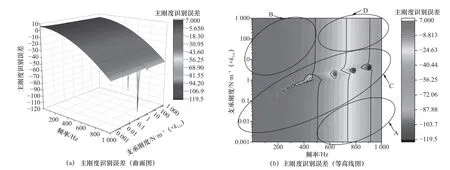
图4 不同支承刚度时轴承主刚度识别误差

图5 不同支承刚度时轴承主阻尼识别误差

从图4 中可以看出，在B 区域，即频率比较小、支承刚度比较大时，此时主刚度识别精度比较好；在A、D 区域，当频率增大后，无论支承刚度大小，其识别精度都有所下降；在C 区域，轴承主刚度识别误差存在较大波动，主刚度识别精度较差。

从图5 可以看出，在B 区域，即频率比较低时，此时主阻尼识别精度比较好；在A、D 区域，频率比较高时，明显可以看出，主阻尼识别误差有所增大；在C 区域，轴承主阻尼识别误差存在较大波动，主阻尼识别精度较差。

若将上述识别误差图的4 个部分分为3 个等级，识别精度“较好”部分表示为“++”，识别精度“次之”部分表示为“+”，精度“很差”部分表示为“-”，当支承刚度变化时，试验台支承刚度对轴承动特性系数识别精度的影响规律总结见表2。

从表2 中可以看出，B 部分刚度阻尼识别精度较高，所以支承刚度在B 部分选取比较合适，支承刚度的选取范围大概为试验台支承刚度的1～1 000 倍，大小为7.452×108～6.9×1011N∙m-1，激振频率的选取范围大概在30～400 Hz。

3.3 支承阻尼的影响分析

若支承阻尼为倒置式试验台支承阻尼的0.001～1 000 倍，在激振频率为0～1 000 Hz 时的动特性识别精度分别如图6 和图7 所示。为方便分析，将图分为A、B、C、D、E 这5 个部分，分别代表不同频率和不同支承阻尼时对应的主刚度和主阻尼识别误差。

图6 不同支承阻尼时轴承主刚度识别误差

图7 不同支承阻尼时轴承主阻尼识别误差

从图6 中可以看出，在A、B 区域，即频率比较小时，此时主刚度识别精度比较好，在D、E 区域，当频率增大后，无论支承阻尼大小，其识别精度都有所下降，在C 区域，轴承主刚度识别误差存在较大波动，主刚度识别精度较差。

从图7 可以看出，在A、B 区域，即频率比较低时，此时主阻尼识别精度比较好，在D、E 区域，频率比较高时，主阻尼识别误差有所增大，在C 区域，轴承主阻尼识别误差存在较大波动，主阻尼识别精度较差。

若将上述识别误差图的5 个部分分为3 个等级，识别精度“较好”部分表示为：“++”，识别精度“次之”部分表示为“+”，精度“很差”部分表示为“-”，当支承阻尼变化时，试验台支承阻尼对轴承动特性系数识别精度的影响规律总结见表3。由表3 可以看出，A 和B 部分刚度阻尼识别精度较高，所以支承阻尼在A 和B 部分选取都比较合适，也就是说支承阻尼对动特性识别精度的影响几乎可以忽略，激振频率的选取范围大概在30～280 Hz。