一种平面差分传声器阵列的声成像算法

刘均建,胡顺仁,李 双,2,3,陈明家

(1.重庆理工大学 电子与电气工程学院,重庆 400054;2.重庆金美通信有限责任公司,重庆 400030;3.重庆大学 微电子与通信工程学院,重庆 400044)

0 引言

声源定位是指利用传声器接收到的声音信号确定声源的位置,目前被广泛应用于电子、交通、机器人、汽车噪声源定位等领域[1-3]。基于传声器阵列的声成像技术[4]是声源定位的主要方法之一,指根据传声器阵列采集到的多通道声压数据,通过信号处理算法将声音信号在空间的分布转换成图像信号,使得声源在空间的分布情况可视化,从而对声源位置进行快速定位。利用声成像定位声源可直观获得声源的位置,获得了广泛应用。

传声器阵列阵型一直是声成像领域的研究热点。传声器阵型设计主要是将传声器排布在不同的位置来达到提高成像分辨率等目的,最初的设计几乎都是规则的几何阵列,如十字阵列、矩形阵列和圆形阵等。但使用规则的几何阵列进行声成像时会出现空间混叠现象,导致出现干扰主瓣识别的栅瓣[5]。为了解决栅瓣问题,Prime等[6]提出了不规则的单臂和多臂螺旋阵列。在单臂螺旋设计方面,阿基米德螺旋阵列[7]运用螺旋公式,对螺旋半径和圈数进行调整设计从而控制整个阵列的形状及孔径大小。Snellen等[8]采用一个32阵元的单臂螺旋阵列对飞机的过顶噪声电平变化进行分析。Underbrink多臂螺旋阵列[6]在Dougherty提出的指数多臂螺旋阵列基础上进行改进,每个传声器对阵列的孔径面积进行了均分,成像几乎不存在栅瓣问题,且可在一定程度上减少传声器的数量。针对Underbrink多臂螺旋阵列,Amaral等[9]进一步改进,每个环上分布不同数量的传声器,阵列在设计上更加灵活,极大提高了动态范围。刘哲等[10]对阵列的特性进行了研究,提出了一种优化的64阵元平面螺旋阵列,该阵列具有较窄的主瓣宽度和较低的旁瓣级,并使用该阵列实现了对汽车发动机噪声的定位。Xiong等[11]设计了二维斐波那契阵列,在1～3 kHz的频率范围内具有更低的最大旁瓣电平和更高的分辨率,并将其应用于轨旁声学轴承故障诊断。张孟浩等[12]提出了优化的轮形阵列,成像的最大旁瓣比通用轮形阵列最大旁瓣水平降低了3 dB。虽然以上阵列能够处理栅瓣的问题,但要提高成像的分辨率,除采用更为复杂的算法以外,还可通过增加麦克风数目或者增大阵列孔径的方法实现。例如,司文荣等[13]为对变压器铁心松动进行定位研究,设计的传声器阵列采用了118个麦克风;Kümmritz等[14]采用1个斐波那契阵列和1个星型阵列测量火车的噪声分布和来源,每个阵列各由120个传声器构成;曹浩等[15]采用阵列孔径达4 m的传声器阵列对某800 kV变电站噪声进行声成像定位研究。除了对阵列孔径和阵元数进行研究,另一个研究方向就是采用分布式麦克风阵列来进行定位。例如,李洪兵等[16]提出了一种L型分布式面阵的二维高精度角估计方法,在降低硬件成本和计算复杂度的同时提升了测角精度;Firoozabadi等[17]利用一种T形圆形分布式麦克风阵列对三维的多声源进行定位;Choi等[18]提出了一种基于分布式多球阵列三维声源定位技术,仿真结果表明其可以准确定位三维空间中的多个声源位置。

近年来,基于差分域的稀疏阵列的提出,例如一维嵌套阵[19]等,使得一个N元的稀疏阵列可以达到O(N2)的自由度,从而大幅提高目标检测的个数。一维稀疏阵列又迅速被拓展到二维稀疏阵列,使得二维波达方向估计的目标数量大幅度提高。但已有基于差分域的二维稀疏阵列的研究主要应用于波达方向估计。例如,王璐[20]利用基于平面嵌套阵的MUSIC算法进行DOA估计;李江欣[21]基于差分麦克风阵列对低仰角目标的测向进行研究;何赛娟等[22]基于差分麦克风阵列和语音稀疏性对多声源的方位进行估计;丁少为等[23]利用基于差分传声器阵列期望最大化的方法使得混响噪声环境下对多源的估计精度进一步提升。然而,基于差分域的二维稀疏阵列在声成像领域还鲜有应用。

为了减少已有声成像定位系统所使用的阵元数目,提出一种基于差分域的平面传声器阵列的高分辨率成像方法。通过对接收信号的协方差矩阵进行向量化,得到原始阵列的差分阵,然后基于差分阵进行声成像。利用二维嵌套阵列等典型平面稀疏阵列结构,可在差分域获得具有更高自由度的均匀矩形阵列,从而用极少数量的传声器获得高分辨的声成像。仿真结果表明,基于平面差分麦克风阵列的声成像算法能够分辨2个相隔很近的声源信号,相比基于物理阵元的声成像算法具有更高的分辨率。

1 声成像信号模型

声成像信号模型如图1所示。

图1 声成像信号模型示意图

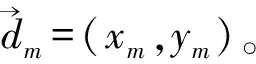
(1)

式中:nm(t)为第m个阵元在t时刻的观测噪声;si(t)为第i个信号源在t时刻的值;f为声源信号中心频率;λ为声源信号的波长;τmi表示第i个信号到达第m个阵元时相对参考阵元(原点位置处的阵元)的时延,表达式为

(2)

令

x(t)=[x1(t),x2(t),…,xM(t)]T

s(t)=[s1(t),s2(t),…,sD(t)]T

n(t)=[n1(t),n2(t),…,nM(t)]T

式中:x(t)、s(t)、n(t)分别表示接收信号向量、信号源向量和接收噪声信号向量,[·]T表示向量的转置。则式(1)的向量表达形式为[20]

x(t)=As(t)+n(t)

(3)

A为平面阵列的阵列流形矩阵,可表示为

A=[a(θ1,φ1),a(θ2,φ2),…,a(θD,φD)]

(4)

导向矢量a(θi,φi)为

(5)

声成像算法是将声源面进行网格化,基于传声器阵列接收到的空间声音信号x(t),对离散的网格点逐一求得对应的功率输出值,将每个网格点的功率值作为图像的像素值,进而获得对应图像。因此,声成像得到的图像中的亮斑或亮点对应输出功率的极大值位置,最终对应声源的估计位置。

2 基于差分域常规波束形成的声成像算法

传统波束形成算法虽然计算量小、稳健性和鲁棒性好,但其分辨率受限于瑞利限,分辨率较低。为了提高对声源的分辨能力,提出了基于平面嵌套阵差分域的虚拟阵列的波束形成算法,通过构建虚拟阵列,增加阵列有效孔径和自由度,从而提高阵列的空间分辨能力。本算法先对阵列接收信号协方差矩阵进行向量化,得到差分阵;然后基于差分阵利用常规波束形成算法完成所有方向的功率扫描,获得声成像图。

根据信号与噪声的假设,阵列接收信号的协方差矩阵为

(6)

z=vec (Rxx)=

(7)

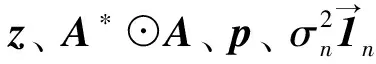
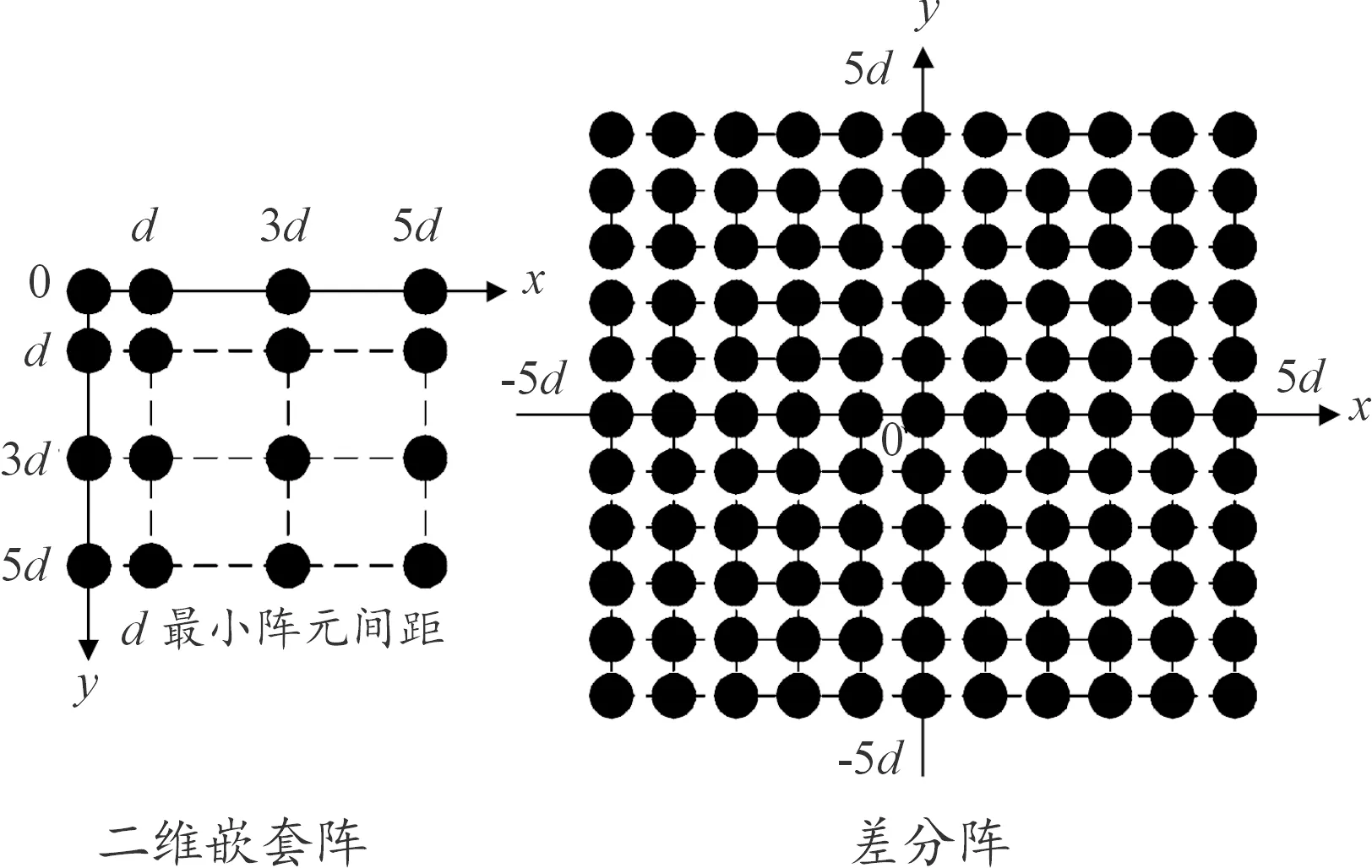
图2 二维嵌套阵列及其差分阵示意图

(8)

其中:B=「b(θ1,φ1),b(θ2,φ2),…,b(θD,φD)⎤;e是中间元素为1、其余元素全为0的向量。按照差分阵阵元位置,重排之后的虚拟阵列导向矢量记为

(9)

下面基于差分阵利用常规波束形成算法完成所有方向的功率估计。

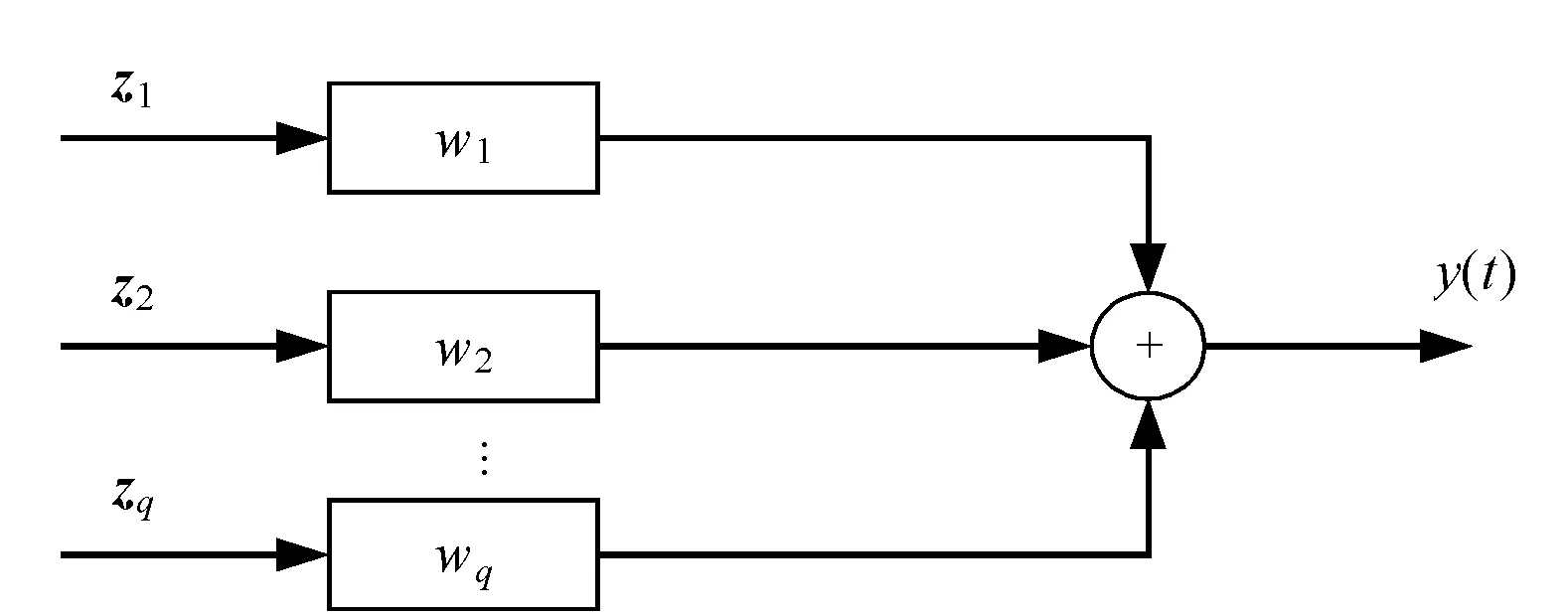
图3 虚拟阵列波束形成示意图

(10)

可得虚拟阵列波束形成的输出功率为

(11)

其中R为差分阵列输出信号的协方差矩阵。由得到的虚拟阵列波束形成在各个方向的输出功率即可得到声源的声成像图。

在二维嵌套阵列的设计中,嵌套阵内和嵌套阵间的阵元间距选择十分重要,阵元间距过大会导致构建的差分阵出现孔洞;阵元间距过小会导致构建的差分阵出现过多冗余而无法达到理论上的最大自由度,进而影响最大分辨率。虽然基于差分域的方法会增加运算量,且只能用于非相关和弱相关的情况,但是通过构建虚拟阵列能够增加阵列有效孔径和自由度,从而提高阵列的空间分辨能力。

3 仿真结果分析

为了验证所提声成像算法的性能,以二维平面嵌套阵列[22]为例,将所提出的算法与阿基米德螺旋阵列[7]、渐开螺旋线阵[25]、annular阵列[8]进行比较。除annular阵列阵元数设置为90外,其他阵列阵元数都为81。为进一步验证二维嵌套阵列的性能,阵元数分别设置为81和49。所有比较阵列采用常规波束形成算法完成功率估计。二维平面嵌套阵列的最小阵元间距为半波长。阿基米德螺旋阵的螺线间距参数值设为2.5,螺线旋转范围为(0,8π),步长设为0.1π。渐开螺旋线阵列的基圆半径为10,传声器环的数目为9,螺旋臂数目为9。annular阵列的基圆半径为10,传声器环数为9,螺旋臂数目为10。阿基米德螺旋阵、annular阵、渐开螺旋线阵及嵌套阵阵元位置如图4(a)—(e)所示。所有实验仿真均在Windows系统下的Matlab R2016a软件中进行。

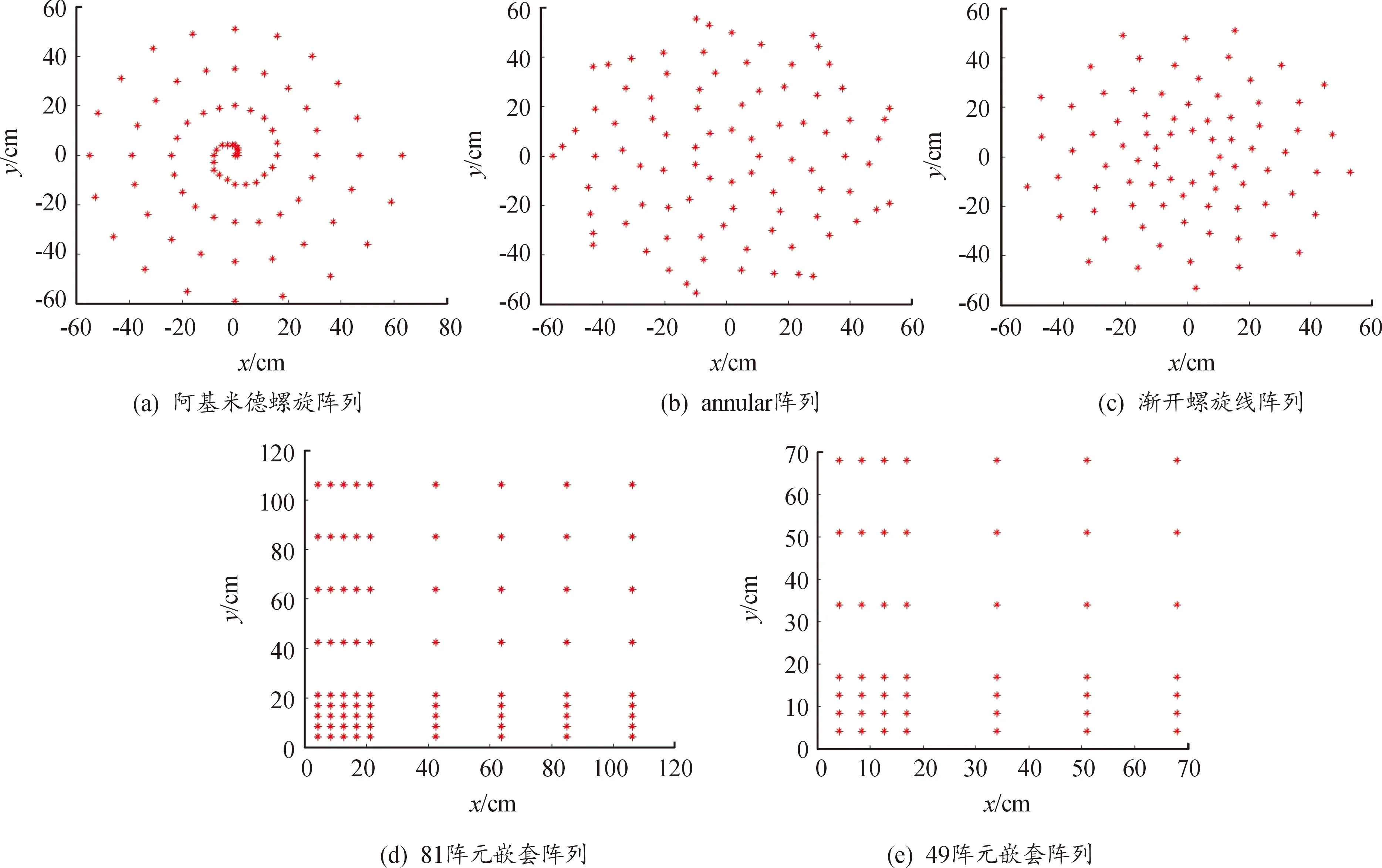
图4 不同阵列阵元位置示意图

在实际应用场景中,多声源同时出现的情况非常多见。对距离相近的多声源检测时,声成像定位的分辨率尤为重要。实验设置声源频率为4 000 Hz,功率大小一致,信号位置分别位于(-27.5°,42.5°),(-21.5°,38.5°),(-10.5°,30.5°),(0.5°,33°),(10°,31.5°),(15.5°,41°)方向,采样快拍数为1 000,信噪比为10 dB,扫描角度网格最小划为0.5°。阿基米德螺旋阵列、annular阵列、渐开螺旋线阵列、81阵元、49阵元的二维嵌套阵列的空间功率谱估计及声成像结果分别如图5和图6所示。

在空间谱方面,从图5的(a)—(d)仿真结果可看出,基于物理阵列空间谱的主瓣都较大,且对于2个相距较近的声源,其主瓣大部分存在重合,而基于嵌套阵的差分阵声成像的功率谱图的主瓣更小、对较近的声源分辨率更高;其次,从图5的(e)仿真结果可以看出,在嵌套阵阵元数远小于其他物理阵列的情况下,基于嵌套阵差分阵的空间谱图像的主瓣相对于其他物理阵列的主瓣依然更小,但对声源位置的估计存在0.5°的估计误差;最后,从图5的(d)、(e)可以看出,49阵元嵌套阵在主峰旁存在较少的旁瓣干扰,而81阵元嵌套阵的主峰旁几乎不存在旁瓣干扰,随着嵌套阵阵元数的增加,其主瓣宽度更小,定位分辨率更高。

根据图5可得到各个阵列估计的声源具体位置与真实声源的位置差异如图6所示。从图6可看出,所有阵列都可分辨出所有信源,在阵元数为81的情况下,所提算法对所有声源的位置估计均不存在误差,而阿基米德螺旋阵列在(-21.5°,38.5°)处估计的声源位置为(-22°,39°),在方位角和俯仰角上均有0.5°的估计误差,定位的均方根误差为0.204°;annular阵列在(-10.5°,30.5°)处估计的声源位置为(-10.5°,31°),在俯仰角上存在0.5°的估计误差,定位的均方根误差为0.144°;渐开螺旋线阵列在(-27.5°,42.5°)和(-21.5°,38.5°)两个方向处的声源估计位置分别为(-27°,42°),(-22°,39°),在方位角和俯仰角上均存在0.5°的估计误差,定位的均方根误差为0.289°。49个阵元数的嵌套阵在(-27.5°,42.5°)、(-21.5°,38.5°)和(-15.5°,41°)三个方向处的声源位置估计存在误差,但是其均方根误差与81阵元的渐开螺旋线阵的相同。

在成像图方面,首先,从图7(a)—(d)可以看出,在阵元数相同的情况下,基于物理阵列的声成像的定位亮斑面积较大,在成像图的四周均出现干扰,而基于嵌套阵差分阵的声成像的定位亮斑面积更小;其次,从图7(e)可以看出,在嵌套阵阵元数远小于其他物理阵列的情况下,基于嵌套阵差分阵的声成像结果依然更好;最后,从图7(d)、(e)可以看出,49阵元嵌套阵在声源周围有较多干扰,而81阵元嵌套阵声成像结果几乎没有旁瓣干扰,对与两相近的声源随着阵元数的增多和阵列孔径的增大,基于嵌套阵的差分阵阵列的声成像的分辨率更高,能够更好地对声源进行定位。

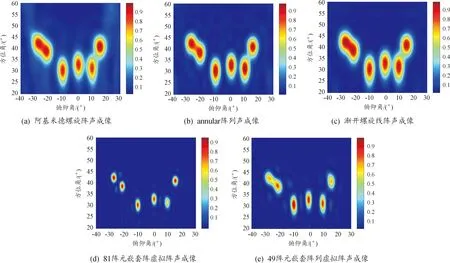
图7 六声源声成像图

由于声成像定位的声场条件较为复杂,不同的信噪比可能对声成像定位精度的影响不同,故通过改变信噪比来研究其对所提算法定位精度的影响。设置信号方向为(-27.5°,42.5°),(-21.5°,38.5°),(-4.5°,28.5°),(1.5°,33°),(10.5°,36.5°),(15.5,41°),噪声为加性高斯白噪声,信噪比分别设置为-10,-5,0,5,10,15和20 dB,快拍数设定为1 000。进行50次蒙特卡洛实验,得到各阵列对声源估计误差与信噪比的关系如图8所示。

从图8可以看出,基于渐开螺旋线阵的定位均方根误差最大,在低信噪比的条件下,所提算法对声源的定位误差最小,当信噪比大于0后,基于annular阵列的定位精度最佳,但本文所提算法使用的阵元数远小于其余阵列使用的阵元数。

综上所述,在低信噪比条件下,所提算法可以使用更少阵元数获得更窄的定位主瓣宽度,其定位精度同样更优,因此对于声场条件复杂的声成像定位场景,所提算法更为适用。

4 结论

提出了基于差分域的平面传声器阵列的高分辨率成像方法。以二维平面嵌套阵为例,在其差分域得到嵌套阵对应的差分阵阵元,传声器阵列在不同位置采集到的噪声信号通过处理之后得到与差分阵阵元位置对应的虚拟信号,再将该信号作为波束形成的输入信号对噪声进行声成像定位。实验仿真结果表明,与现有基于物理阵元的声成像对比,基于差分域的二维平面嵌套阵对应的虚拟阵列波束形成算法对单个和多个噪声信号均有良好的定位效果;相比基于相同物理阵元的声成像,所提出方法的主瓣更窄、分辨率更高且能够分辨相近的声源;在使用嵌套阵列阵元数远少于其他物理阵列的情况下,所提出方法的主瓣宽度依然更低,也能实现对近距离声源的定位,有较强的抗噪声能力和较高的空间分辨能力。

为推导方便,本文中假设声源目标为窄带信号,但很多实际场合的声音信号为宽带信号,故后续将对宽带信号的差分域声成像展开详细研究。2个嵌套阵为异面(即三维立体空间)的嵌套阵是较有意义的研究内容,后续会展开相关研究。下一步研究工作还包括将所提算法应用于真实声学数据场景,分析算法在真实数据场景下的性能。