全局接地系统非线性参数迭代学习分析方法研究

李小川,何智颖

(1.重庆理工大学 机械检测技术与装备教育部工程研究中心,重庆 400054;(2.重庆大学 输配电装备及系统安全与新技术国家重点实验室,重庆 400030;3.重庆理工大学 时栅传感及先进检测技术重庆市重点实验室,重庆 400054)

0 引言

全局接地装置不仅为各种电气设备提供一个公共的参考地,而且在发生故障或雷击时,能够将故障电流或雷电流迅速散流,限制地电位的升高,保证人身和设备安全,因此接地是确保电力系统安全稳定运行的重要条件,其可靠性及安全性能一直受到设计和生产运行部门的高度重视[1]。接地装置的冲击阻抗可反映接地系统的雷电防护性能,降低接地阻抗是提高线路耐雷水平,保障线路运行可靠性的关键措施。然而,在国内外的输电线路防雷分析计算中,接地阻抗通常采用特定值的集中参数电阻来模拟。在《交流电气装置的接地设计规范》(GB/T50065—2011)中,工频接地电阻与冲击系数的乘积被作为接地阻抗的数值[2],并用它来表征接地装置的冲击性能。这种模拟方法常常导致计算结果与实际情况差异较大,给线路防雷计算带来了很大的误差。

雷电冲击下接地装置上会有明显的电感效应和火花效应,具有复杂暂态行为[3],传统的接地参数分析方法主要为试验方法[4],将试验测得冲击电压和冲击电流的幅值之比作为冲击电阻,然而这种取幅值之比的方法不能完全反映由电感效应和火花效应引起的复杂暂态过程,原因主要为电压幅值和电流幅值对应的时刻之间有较大的时延[5],而较大时延是系统存在非线性参数的有力证据。

已有的研究表明:高幅值的冲击电流入地时,土壤内部某些部分的场强值超过土壤临界击穿场强,从而产生激烈的土壤放电现象[6]。通过试验发现,土壤放电现象造成了土壤电阻率的显著降低,传统分析方法忽略了这种暂态特性,在面对日益复杂的接地系统及其互联的弱电系统时,难以准确分析电磁环境对设备造成的危害[7]。

接地系统的复杂暂态特性之一为冲击大电流作用下土壤会发生剧烈的火花放电现象,引起土壤电阻率的剧烈衰减。对这个现象的准确分析存在以下2个困难。首先,由于土壤为固液气三相复合介质,土壤放电的冲击暂态过程使得土壤可能具有时变的电感特性和电容特性;其次,试验回路中存在调波电感、调波电阻等元件,这些元件也参与了系统的冲击响应,导致难以直接从系统全局响应中直接反映土壤非线性参数的变化规律。

由于土壤放电过程发生在土壤介质内部,这也给正确认识土壤放电区域带来了重重困难。长期以来,由于受到研究手段的限制,人们对于土壤放电区域的了解所知甚少。然而,为了满足接地装置冲击特性分析必须考虑土壤放电现象的要求,常常都是采取简化的方式,在人为假设的土壤放电区域结构的基础上,建立土壤放电模型并计算相应的土壤放电特性电参数[6]。实际上,这种基于人为假设放电区域来计算土壤放电参数的方法,无疑对准确计算接地非线性参数增加了束缚,由于放电区域的假设不同,因而放电参数的计算结果也不尽相同,导致众多研究成果差异性较大。

在试验方法难于准确获取接地电阻参数的前提下,受20世纪七八十年代提出并广泛得到应用的迭代学习控制算法[8-9]的启发,应用其无模型思想[10-12]以及其在非线性时变问题中的强适应性[13-15],建立一种基于迭代学习的、所需先验知识少、无需复杂模型的全局接地系统非线性参数的分析方法。通过迭代算法,基于文献[16]的试验数据,跟踪土壤放电过程的电流和电压曲线,突破传统方法难于掌握接地电阻的非线性变化规律、依赖较多人为假设的弊端,解决非线性系统中未知时变电阻率的准确获取难题,并与文献[16]的电阻率计算结果进行对比分析来说明方法的有效性。

1 问题描述

图1所示是快速冲击下的土壤击穿过程的等效电路[16]。ui(t)和uo(t)分别为输入电压和输出电压;Ls=0.04 μH为固有电感;Cs=0.15 μF为主电容,其两端电压差为ucs(t);Rcir=0.01 Ω为回路电阻,Lcir=0.35 μH为回路电感,Is(t)为通过电阻Rcir以及电感Lcir的电流;Ccir=20 pF为回路电容,通过该电容的电流为Icir(t),该电容两端的电压差为ucir(t);Lrod=0.1 μH为接地导体电感;I为输出电流;L=7 mH为试品土壤电感;R1、R2分别为击穿前电阻和击穿后电阻;Csand为试品土壤电容;开关SW1用于产生快速冲击的电压和电流,开关SW2用于模拟土壤击穿前(SW2断开)和土壤击穿后(SW2闭合)的情况。

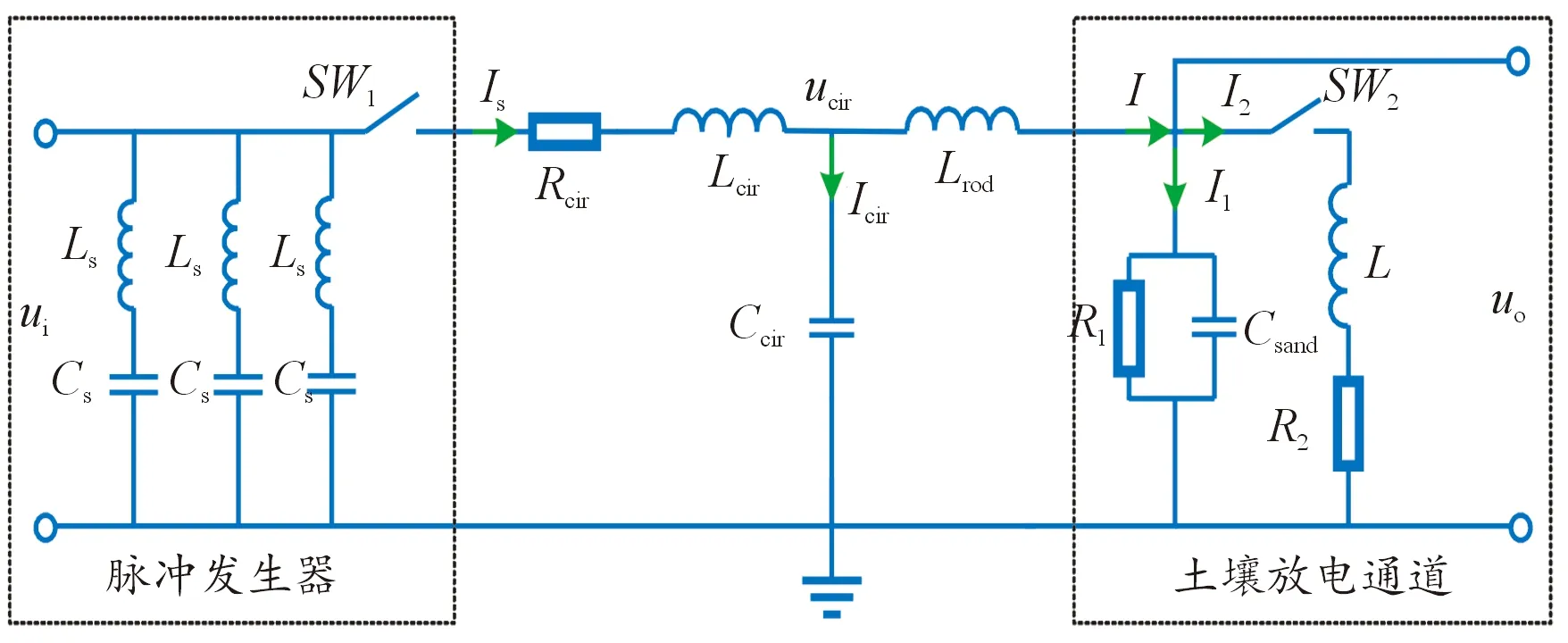
图1 等效电路图

首先,在开关SW1断开的情况下,对脉冲发生器进行充电,使之达到预定电压upre后停止充电并同时闭合开关SW1,可以得到脉冲发生器输出电流Is(t)与输出电压ui(t)满足如下微分方程:

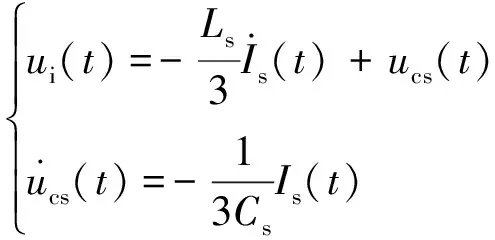
(1)

冲击电流从脉冲发生器传递到土壤的过程可用微分方程表述为:

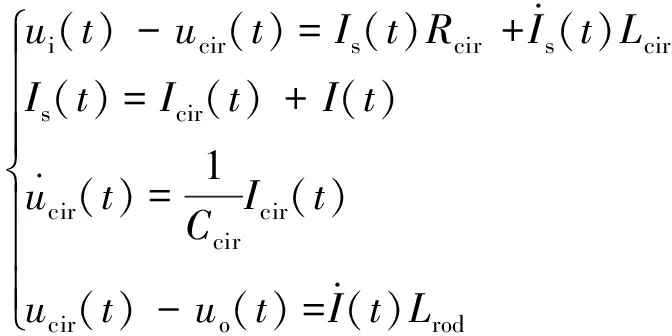
(2)

由文献[16]可知,土壤击穿过程中,Csand的作用可以忽略。因而在简化模型中,不考虑电容Csand的影响。此时,土壤击穿前有

uo(t)=I(t)R1

(3)

土壤击穿后有

(4)

由于击穿前电阻和击穿后电阻R1、R2受土壤湿度、盐度、紧密度等因素影响较大,而冲击过程会产生较大的电流,产生复杂的热效应和电击穿效应,从而使土壤属性发生了改变[17-18],为准确确定R1、R2带来了困难。因此,拟基于式(1)—式(4),建立系统的数学模型,并基于迭代学习控制的思想,利用实测快速冲击下的土壤电压和电流信号,准确确定电阻R1、R2的取值,便于后续进行土壤暂态非线性参数的分析。

2 电阻变化对输出电压、电流波形的影响分析

当电阻值R1、R2取不同值时,输出电压uo(t) 的波形与输出电流I(t)的波形也有差异。因此,分析电阻变化对输出电压、电流波形的影响有利于制定合理的迭代学习策略。选取6个指标来对电阻变化对输出电压、电流波形的影响进行评价,如表1所示。分别计算不同冲击电压下,不同阻值下的影响评价指标情况。

表1 电阻变化对输出电压、电流波形的影响评价指标

图2给出了输入电压(即冲击电压)初始值为27 kV时的影响评价指标情况。

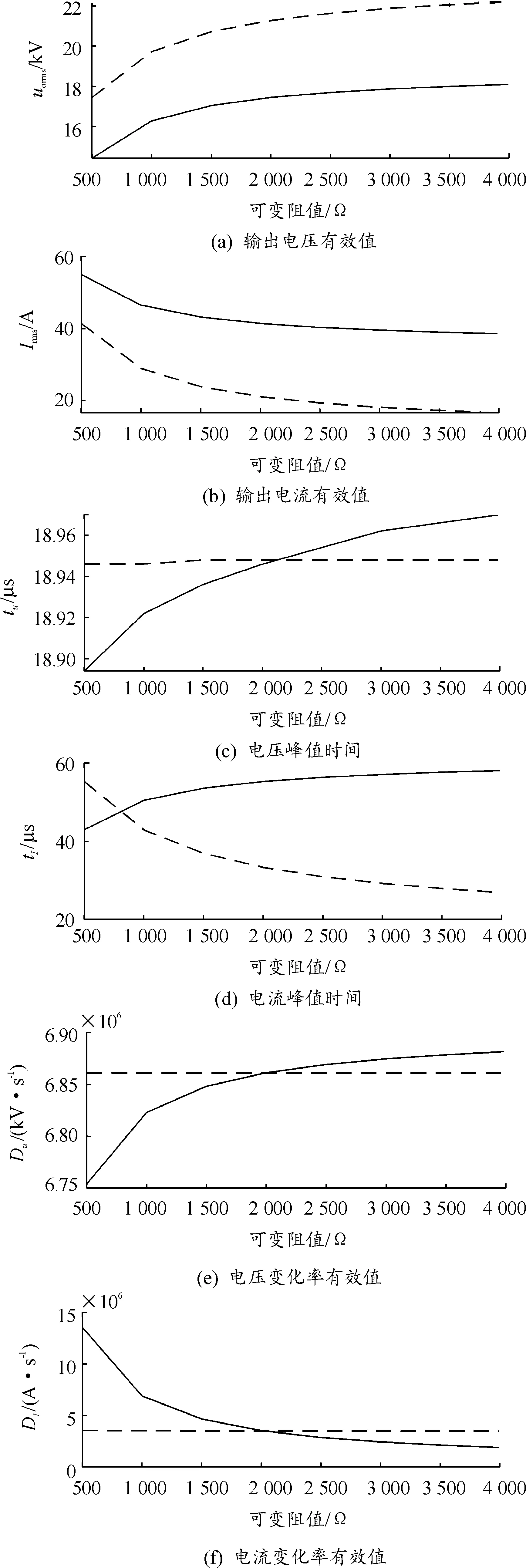
注:实线表示R1为可变值,R2=1 000 Ω时的情况;虚线表示R1=2 000 Ω,R2为可变值时的情况。

选取多组冲击电压初值以及R1、R2值,分别计算表1中所列影响评价指标,均可得到与图2相近的结果。若定义某影响评价指标Fi在区间[Rmin,Rmax]变化时对电阻Rj的敏感程度为:

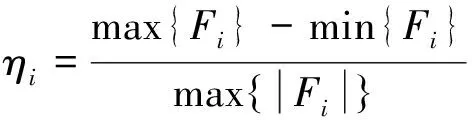
(5)

则敏感程度ηi越大,表明指标Fi对电阻Rj的阻值越敏感,即Rj阻值的变化对Fi变化影响越大。

分别计算图2所示仿真工况下的不同影响评价指标对不同电阻的敏感程度,结果如表2所示。可得出如下结论:

表2 影响评价指标对不同电阻的敏感程度

1) 输出电压有效值、输出电流有效值、电流峰值时间、电流变化率有效值对电阻R1的变化敏感;

2) 输出电压有效值、输出电流有效值、电流峰值时间对电阻R2的变化敏感;

3) 输出电压有效值对电阻R1的变化的敏感程度与对电阻R2的变化的敏感程度接近,输出电流有效值、电流峰值时间对电阻R2的变化更敏感。

3 迭代学习分析方法

根据第2节的结论,设计全局接地系统非线性参数的迭代学习分析方法,其流程如图3所示。为降低修正过程的运算量,利用迭代学习对击穿前后电阻的修正过程分为粗修正和精修正。粗修正过程不考虑接地电阻随时间的变化情况,以获取精修正过程的初值。而精修正过程则是根据实时的电压、电流情况对电阻再行修正。

第N+1次粗修正电阻值由第N次粗修正电阻值进行修正得到,即

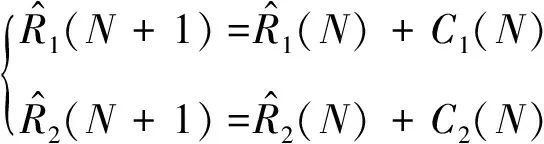
(6)

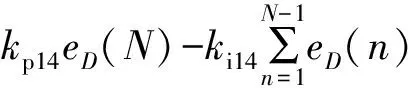
(7)

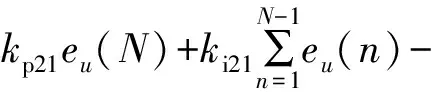
(8)

式中:学习增益kpmn>0,kimn≥0,其中,输出电压有效值误差eu(N)、输出电流有效值误差eI(N)、电流峰值时间误差et(N)以及电流变化率有效值误差eD(N)分别为:

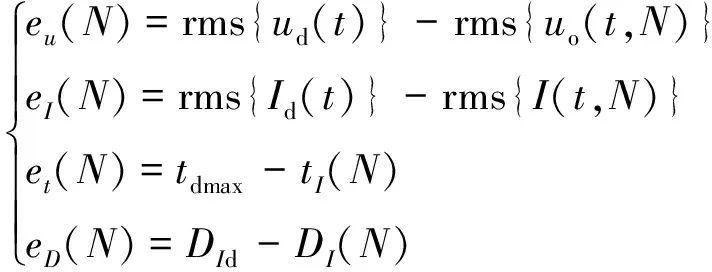
(9)

式中:ud(t)为实测输出电压,Id(t)为实测输出电流,tdmax为实测输出电流的峰值时间,DId为实测电流变化率有效值。

在粗修正电阻的基础上,利用迭代学习算法,基于实时测量的电压及电流信号,对接地电阻进行精修正,其中,第j+1次迭代得到的实时电阻值Rm(k,j+1)由第j次迭代的实时电阻值Rm(k,j)通过如下的精修正的迭代学习修正律得到:

Rm(t,j+1)=Rm(t,j)-kmI[Id(t,j)-I(t,j)]+

kmu[ud(t,j)-uo(t,j)]

(10)

4 仿真分析

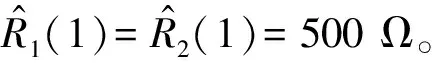
仿真输出的电流波形、电压波形与文献[16]中实测波形趋势如图4所示,仿真得到的实时接地电阻值随时间的变化曲线如图5所示。

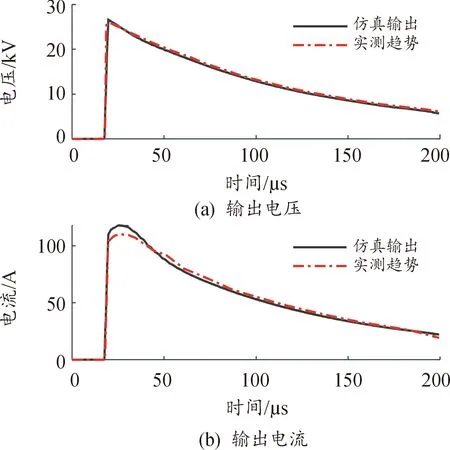
图4 经500次粗迭代以及20次精迭代后仿真结果与实测趋势曲线

图5 经500次粗迭代以及20次精迭代后实时接地电阻值随时间的变化曲线

根据图4和图5,可以得到如下结论:

1) 定性上看,经过500次粗迭代和20次精迭代后,仿真输出的电压波形、电流波形与文献[16]所示的实测数据具有相同的趋势;

2) 定量上看,经过500次粗迭代和20次精迭代后,仿真得到的输出电压最大相对误差为2.82%,输出电流最大相对误差为6.97%。

3) 以随机选取的粗迭代初值为初始量,经过若干次迭代后,得到的接地电阻值随时间变化的趋势呈现出明显的时变和非线性特性,可见,采用迭代学习方法在缺少先验知识的情况下,仍可以对接地系统的时变非线性参数进行一定精度的分析。

5 结论

提出了一种快速冲击作用下的接地电阻迭代学习分析方法,利用迭代学习控制的思想和无模型的特性,无需提前假设非线性电气参数类型,仅根据冲击响应即可获取非线性电参数,一定程度上解决了复杂因素作用下的接地电阻的阻值确定问题。该方法避免了人为假设的误差,提高了计算结果的准确性,为进一步分析土壤放电参数提供了理论依据。

但是,提出的方法仍有一定的不足之处。迭代学习的思想要求从初始值开始,利用迭代学习控制律生成与误差相关的修正量,对拟修正参数不断修正,存在效率低下的问题。此外,迭代学习算法中的学习增益以及初始电阻值是随机选取或凭一定经验选取,其效率、性能受迭代学习增益、初始电阻值的影响较大,从进一步提升算法效率和算法性能、避免迭代算法陷入局部最优值的角度考虑,仍需进一步研究学习增益和初始电阻值的选取方法。