驱动与执行一体式小型汪克尔泵的研究
2023-11-15霍宇轩马明栋张伟荣周晓思张建辉
霍宇轩,张 帆,马明栋,张伟荣,周晓思,黄 茜,谭 天,谢 堂,张建辉
(广州大学 机械与电气工程学院,广州 510006)
0 引言
汪克尔泵最简单的结构是二叶转子或二角转子泵[1-2],这种泵从分类学上属于容积泵[3-6]。可是,如果增加转子中的“叶”或“角”数量的话,原属于容积泵的汪克尔泵会逐渐地向指状蠕动泵[7-9]的方向发展,分类上将不再属于容积泵,模糊地进入无所属分类区域。这说明汪克尔泵所具有的特殊性至今尚未被提炼清楚,其优点也未在应用中明显地彰显出来。传统上,总结汪克尔发动机[10]与汪克尔泵[11-14]的特点都是从其结构简单且紧凑、容积利用率高、能与其他子系统集成等方面去概括。事实上,这些特点应该更具体地总结为汪克尔泵更利于小型化与集成化。研究者对汪克尔泵在生物医学工程[15-20]、小型冷却系统[21-23]和混合器[24-26]等领域已有所探索,但尚未广泛应用。当前,随着大数据与人工智能技术的迅速发展,对万物互联、互通、互动的要求越发迫切,小型化与集成化的机电一体的传感器与执行器将成为制约其发展的瓶颈。芯片尺度的微传感器与微处理器也无法允许驱动与执行间具有分离性的硬连接存在。开发驱动与执行一体化的微流动器件的工作已经严重落后于微纳技术的发展,成为流体领域发展的瓶颈,因此汪克尔泵的小型化与集成化研究具有非常大的现实价值与应用前景。
传统的汪克尔泵的研究内容主要是提高效率与性能、增加容积利用率,具体从流体泄漏现象改进、冲击摩擦现象改善、流场与原理分析三个方面进行。
在流体泄漏现象改进研究方面,1997年,Beard[27]对温克尔旋转式压缩机转子顶端密封进行动力分析,修正了顶端密封的加速度的径向分量和轴向方向的计算公式。2012年,Zhang等[28]利用合理的溢流设计即充分利用间隙容积中高压气体方法提高汪克尔压缩机的效率,并实验证明该压缩机制冷能力提高了约28%。2017年,Garside[29]在进气孔与排气孔设计提升阀,以减少转子和外壳之间的间隙。2018年,Phung等[1]提出了一种转子顶部密封动态行为的建模方法,可精确计算接触力并适应不同密封材料,弹簧、外壳表面刚度以及不同热力学条件。
在冲击摩擦现象改善研究方面,2003年,Lee等[30]研究了汪克尔压缩机中转子与缸体表面的滑动摩擦学特性,得出了最佳初始表面粗糙度。2003年,曹兴进等[31]通过对类摆线压缩机的定转子进行了润滑性能分析,提出了计算定转子间最小油膜厚度的方法。2011年,Zhang等[32]分析了汪克尔泵小型化的摩擦损失影响,确定了微汪克尔泵系统的设计极限。2013年,Zhang等[33-34]综合分析了汪克尔压缩机的7种摩擦损失与各参数的影响,得出了详细摩擦损失方程与摩擦损失对各结构参数的敏感度。
在流场分析研究方面,2015年,Wan等[24]提出了一种基于汪克尔泵几何结构的混合器,模拟了物种浓度的演化。2016年,Wan等[25-26]提出了一种基于汪克尔泵几何结构的混合器,揭示了不同转子转速的颗粒分布的差异与二元混合的浓度分布。2016年,Gronskis等[35]对汪克尔泵的流场采用粒子图像测速技术研究,计算出流体的微粒速度,并得到了局部流体速度。但现有的汪克尔泵研究鲜有从结构方面改进而提升效率。因此,从结构入手进行汪克尔泵的小型化具有重要研究前景。上述研究均未对汪克尔泵的小型化与集成化的机电一体化进行探索、分析或尝试。
本文中提出一种驱动与执行一体式的汪克尔泵,将电机驱动组件集成到汪克尔泵的执行结构中,减少传动路径上的损耗,用圆弧曲线替代缸体型线包络线的复杂曲线设计转子,简化加工。建立了输出转速、输出流量与结构参数、输入电压、磁感应强度的匹配机制。搭建实验平台对泵内工作室流场进行分析,对泵进行转速、流量、压力的测试,最后对结果进行讨论分析。
1 结构原理
1.1 结构设计
汪克尔泵传统上均为驱动与执行分离式设计,给小型化带来了诸多不便。为此,提出驱动与执行一体小型汪克尔泵。考虑到微纳加工时,实现复杂曲线、曲面的加工较为困难,将原来由缸体型线的内包络线组成的三角转子的复杂正投影曲线,设计成贴合缸体内表面的简单的由3条相同且相等交织构成的外凸圆弧曲线。如图1所示,驱动组件除磁铁全部组合在轴上,包括:泵与电机转子公用的偏心轴(电机转子集成在偏心轴内)、电刷架、线圈绕组、励磁性材料,执行组件包括:泵与电机转子公用的偏心轴(泵功能主要集成在同一尺寸偏心轴的光轴部分上)、安装电刷架的前端盖、轴承、外凸圆弧曲线的三角转子以及缸体。其中:偏心轴内对应三绕组线圈转子设置了3个凸台固定电机转子,偏心轴的主轴一端插入轴承安装,电刷架设置有轴承与电机转子配合,并覆盖安装在前端盖的凹层上,2块永久性圆弧形磁铁被埋在缸体两端的槽内,在缸体的两侧并列设置两进两出流道开口。缸体的设计分为2部分:缸体的内表面与外凸圆弧曲线的三角转子相对应的闭合曲线部分;缸体的内表面设置有安装轴承的沉孔及具有防水的后端盖的作用的部分。
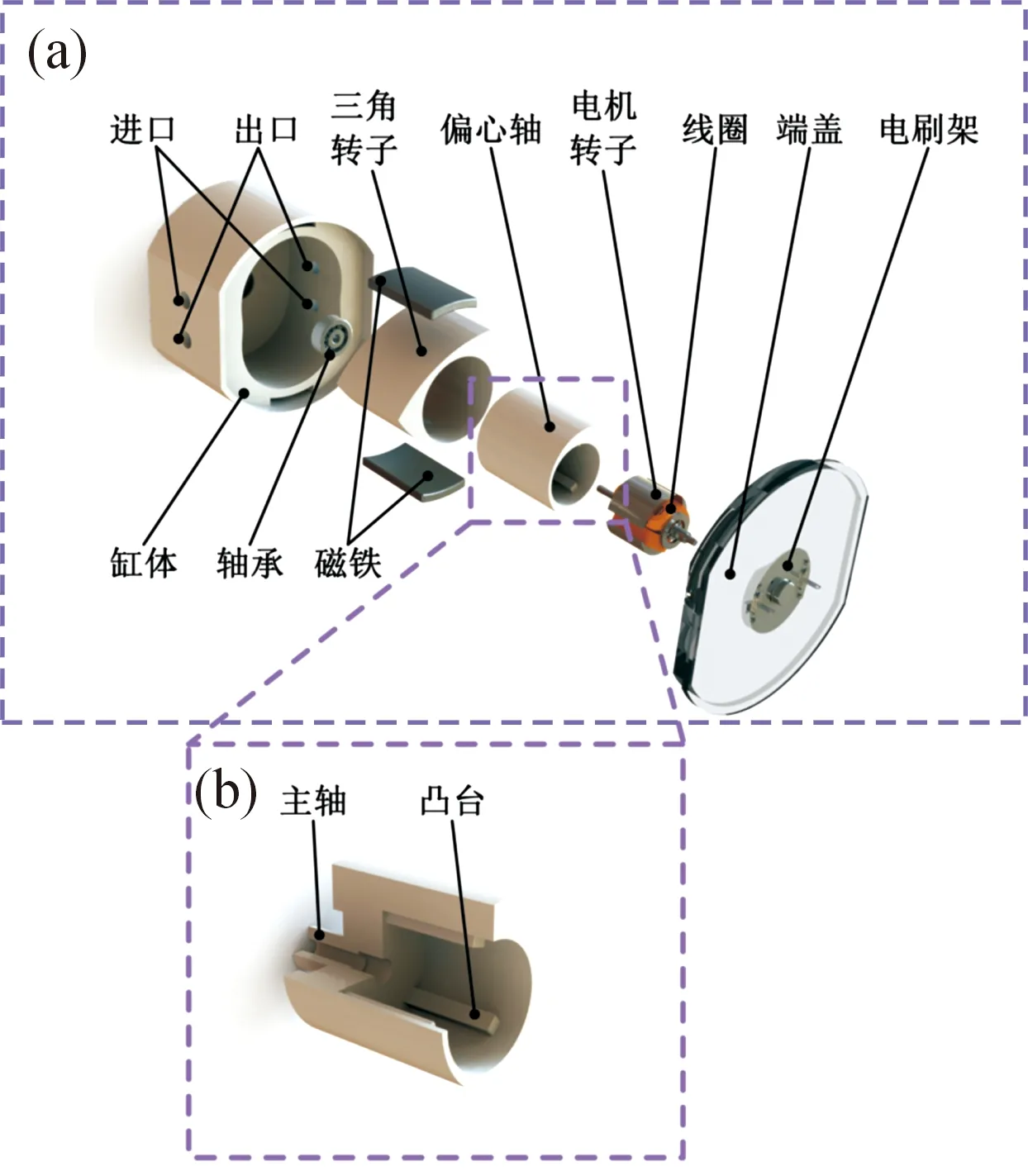
图1 驱动与执行一体式小型汪克尔泵结构示意图
由于电机转子轴与泵的偏心轴的主轴共轴,驱动部分通过电刷、线圈及磁铁把外界的电能转化成偏心轴的转动机械能,偏心轴将转动的机械能传递给外凸圆弧曲线的三角转子,三角转子的偏心复合转动带来三角转子与缸体的内表面间的容积变化,再配合两入两出的出入口,就实现泵的吸入与排出功能。
1.2 型线模型
如图2(a)所示,转子中心Or到缸体型腔中心O的距离为偏心距e,转子中心Or到转子的3个顶点A、B、C的距离皆为创成半径R,αA为顶点A公转角度,αA/3为顶点A的自转角度。缸体型线即转子顶点的运动轨迹,其创成过程(以顶点A为例)是转子的顶点A以创成半径R绕转子中心Or为中心作自转运动,同时转子中心Or绕缸体型腔中心O为中心作公转运动,自转与公转的角速度比为1∶3。故根据其运动规律及几何关系可得到缸体型线的数学表达式与转子上3个顶点A、B、C的相位差关系:
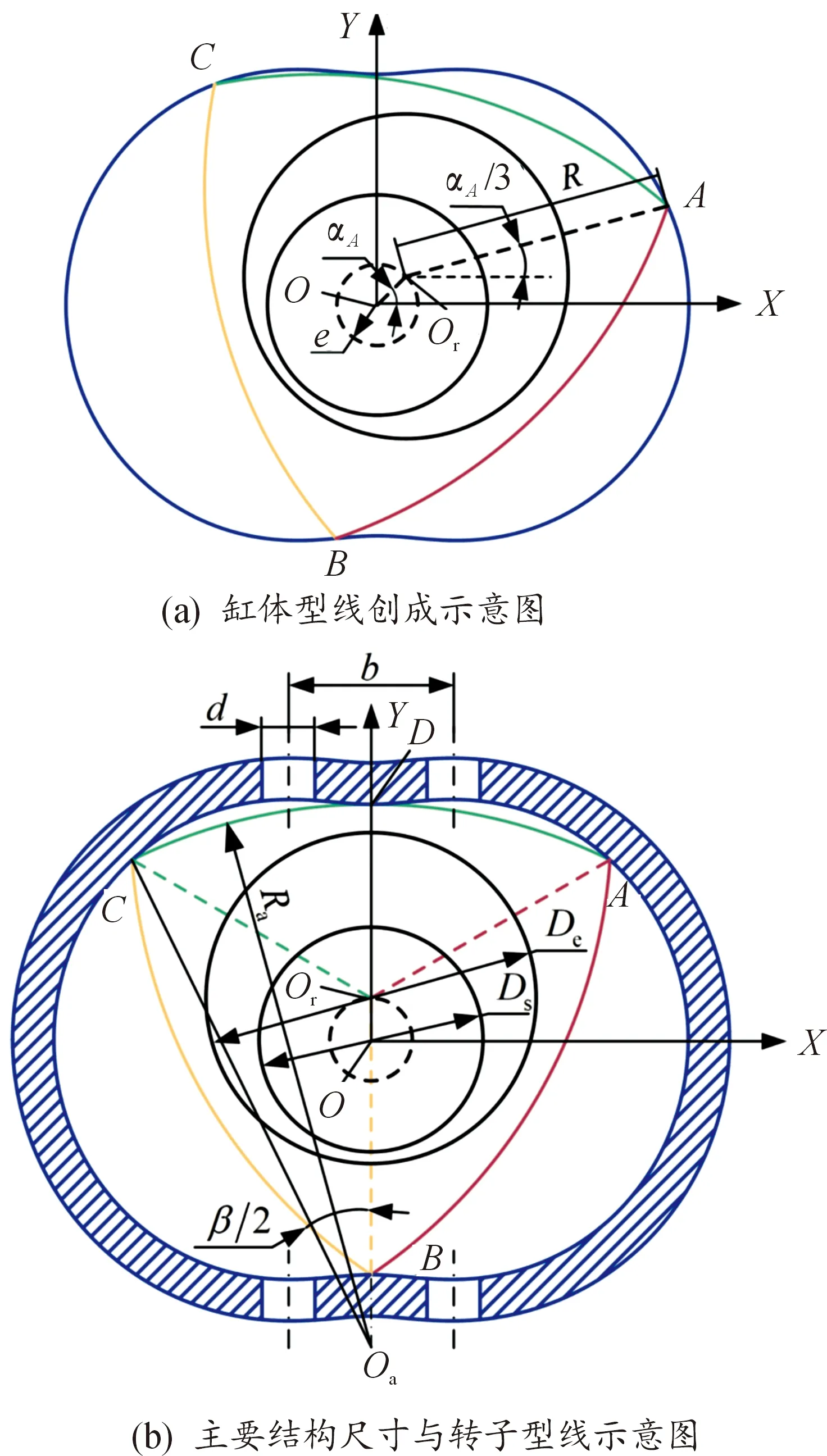
图2 型线模型示意图
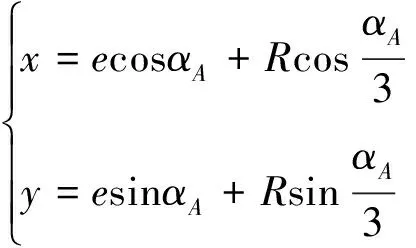
(1)

(2)
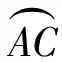
(3)
(4)
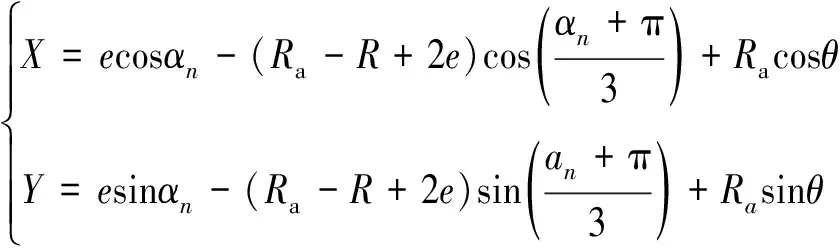
(5)

1.3 工作原理
电机转子绕组上的3个线圈绕组分别引出3个换相片,每个换相片通过电刷及电刷架接入外部直流电。线圈和电机转子铁心在电流作用下产生电磁场,在两侧磁铁产生的磁场中产生转矩驱动电机转子转动。配合电机转子上的换向片,实现电机转子持续转动。
图3为驱动与执行一体式小型汪克尔泵泵送循环的工作原理示意图,电机转子驱动偏心轴绕主轴转动,三角转子作偏心旋转复合运动,即转子绕转子中心Or作自转运动,同时绕缸体中心O作公转运动。偏心轴的转速为三角转子转速的3倍。如图3所示,转子的3个顶点始终保持与缸体的壁面接触,转子的圆弧面与缸体型面形成 3个工作室,转子转动使工作室不断发生容积变化,实现流体“吸入-排出”的泵送循环过程。图3(a)—(g)展示了偏心轴驱动转子顺时针转动,工作室1的容积逐渐增大至图3(d)达到最大,流体从进口1吸入,接着工作室1容积逐渐减少到图3(g)位置,流体从出口1排出的工作过程;图3(g)—(l) 中流体从进口2再次进入工作室1,从图3(j)位置开始流体从出口2排出,即工作室1的第二个泵送工作过程,而工作室2与工作室3分别从图3(e)与图3(h)吸入流体开始其泵送工作过程;图3(a)—(l)中三角转子旋转1周完成1个泵送循环周期,可得出在1个泵送循环周期中,1个工作室完成2次“吸入-排出”的泵送工作过程,即3个工作室完成6次泵送工作过程。
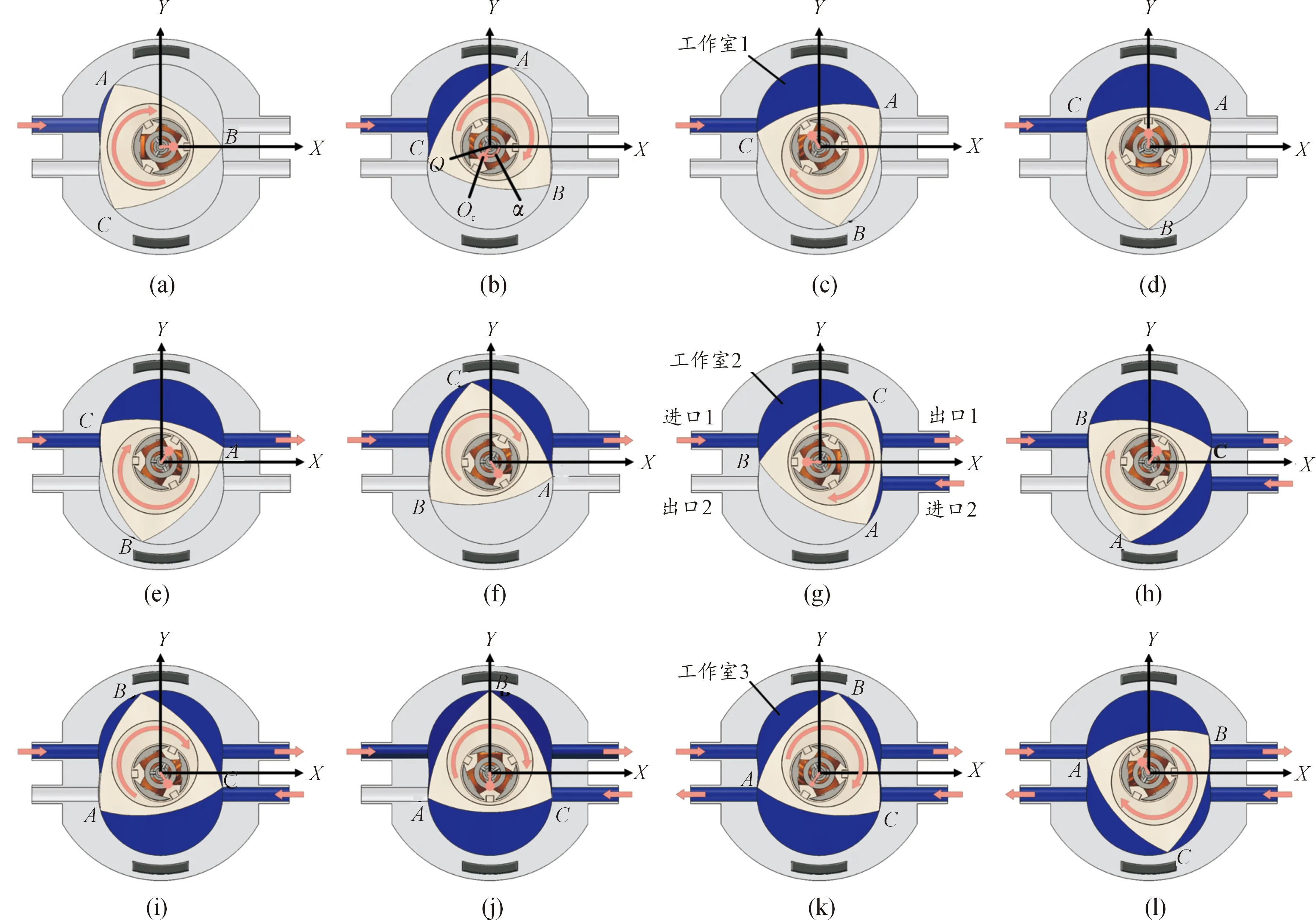
图3 驱动与执行一体式小型汪克尔泵的工作原理示意图
2 理论性能分析
2.1 负载分析
对驱动与执行一体式小型汪克尔泵的转子进行力学分析,转子受到的力包括缸体壁面作用在转子的3个顶点的压力与摩擦力、工作室的流体分别作用在3个工作面的压力[36-38]。
如图4(a)所示,以顶点A为例,将式(1)对时间t作二次微分可得出转子顶点的加速度为
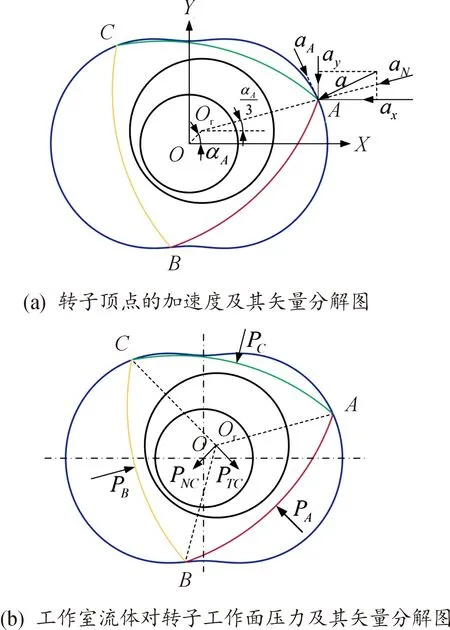
图4 转子动力学模型示意图

(6)
(7)
式中:ax为沿x轴方向的转子顶点的加速度;ay为沿y轴方向的转子顶点的加速度;a为转子顶点的合加速度。
如图4(a)所示,应用矢量分解方法分析,各转子顶点的径向加速度aNn的方向是由转子顶点指向转子中心Or,各转子顶点的切向加速度aTn的方向与缸体壁面切线重合并与转子转动方向相反,可求得其各自大小为
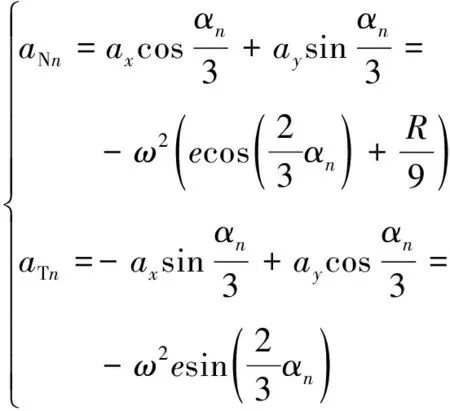
(8)
进而可求得缸体壁面对转子顶点的径向力FNn与切向力FTn:

(9)
式中:m为转子的质量。因此,缸体壁面在转子顶点产生的转矩负载Mwn为
Mwn=(FTn+μ1FNn)R
(10)
式中:μ1为缸体壁面与转子顶点的摩擦因数。
缸体壁面对转子产生的合转矩负载Mw为缸体壁面在转子各个顶点产生的转矩负载的代数和,即:
Mw=MwA+MwB+MwC
(11)
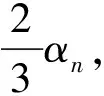
(12)
式中:S为转子工作面的有效面积;pn为对应工作室的流体压力。
将流体作用在工作面的压力分解成径向流体力PNn与切向流体力PTn,径向力方向沿缸体中心与转子中心连线OOr指向缸体中心O,切向力方向垂直缸体中心与转子中心连线OOr并与旋转方向相反,即:
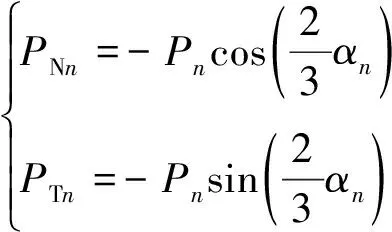
(13)
因此,流体作用在工作面的压力产生的转矩负载为
Mgn=PTne
(14)
其方向与转子旋转方向相反。
工作腔中流体对转子产生的转矩负载Mg为流体在转子各个工作面产生的转矩负载的代数和,即
Mg=MgA+MgB+MgC
(15)
偏心轴承受的转矩负载除了缸体壁面在转子顶点产生的转矩负载Mw和工作腔中流体产生的转矩负载Mg,还包括偏心轴与三角转子间的摩擦转矩Mf:
(16)
式中,μ2为偏心轴与转子间的摩擦因数。故偏心轴承受的总负载转矩Ml为
Ml=Mw+Mg+Mf
(17)
2.2 输出转速分析
对驱动与执行一体式小型汪克尔泵的电机组件进行分析,可得出电机转子电枢产生的电磁转矩M、克服空载转矩M0与总负载转矩Ml平衡的关系,以及输入功率P与电机转子绕组反电势功率P0和电磁功率Pl平衡的关系[36-38],即:
M=M0+Ml
(18)
P=P0+Pl
(19)
电磁转矩M是电机转子的线圈通电后在磁场中产生的转矩之和,可由式(20)求得。
(20)
式中:np为磁极对数;N为线圈总匝数;na为电枢线圈支路对数;I为线圈电流;φ为磁通密度。磁通密度φ与磁感应强度Bδ关系为
(21)
式中:D为电机转子电枢直径;L为转子电枢长度。结合式(20)与(21)得:
(22)
式中:CM为电磁转矩系数,取值只与电机转子的结构参数有关。
电机转子绕组反电势E0是由于电机转子旋转时电机转子上的绕组线圈切割磁力线产生的,可由式(23)求得。
(23)
式中:nr为电机转子输出转速;CE为反电势系数,只与电机转子的结构参数有关。
联立式(18)—式(23)得:
(24)
(25)
式中:E为输入电压;r为电枢绕组总电阻。
式(25)中的第1项为空载转速,与输入电压E成正比,即电机转子输出转速nr随输入电压E增加而增加。式(25)第2项为负载下的转速变化,与电磁转矩M成正比,即当泵的负载Ml增加时电机转子输出转速nr将降低。从式(25)可看出,在一定范围内,电机转子转速nr随磁感应强度Bδ增加而增加,磁感应强度Bδ增加超过一定范围后,电机转子转速nr变化趋于平缓,达到磁通饱和状态。
2.3 输出流量分析
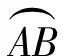
V=FB
(26)
式中:B为缸体深度。
由图5(a)所示,可知面积F有如下关系:

图5 工作室示意图
F=F1-F2-F3-F4
(27)
式中:F1为缸体型线AB与OA、OB所围成的曲边三角形的面积;F2为△OAOr的面积;F3为△OBOr的面积;F4为转子型线AB与OA、OB所围成的扇形的面积。通过积分与几何关系可分别求得:
(28)
(29)
(30)
(31)
式中α为偏心轴转角。
联立式(27)—式(31)整理得:
(32)
从式(32)知,只有第二项是偏心轴转角α的正弦函数,其余各项对于确定的缸体型线都为定值。如图5(b)所示,当偏心轴转角α为π/2+3kπ和2π+3kπ时(k为任意整数),单工作室的面积F分别达到最小值与最大值,故单工作室的一次工作过程的理论排量为
(33)
根据式(32)可画出单工作室的理论容积随偏心轴转角α变化的曲线,如图5(c)所示。分析图5(c)可知,单工作室的理论容积V是周期变化的,一个周期内偏心轴转角α从π/2变化到7π/2,单工作室的理论容积V先增大,至α=2π处达到最大值,再减少,在α=7π/2处达到最小值。可以看出,单工作室在偏心轴转3圈时实现了2次“吸入-排出”的工作过程,故有3个工作室的汪克尔泵的理论流量为
(34)
式中:nr为电机转子输出转速,即偏心轴的转速。可以看出,理论情况下,相同泵参数时,输出流量Q与转速nr成正比,输出流量Q随转速n增加而增加。
3 实验研究
3.1 样机制作
如图6所示,为便于观察转子与偏心轴运动状况以及内部工作室流场,端盖以透明光敏树脂作为加工材料,而缸体、转子和偏心轴以不透明树脂作为加工材料,采用3D打印技术(成型精度为±0.1 mm)制造。驱动组件与执行组件的结构参数如表1所示。
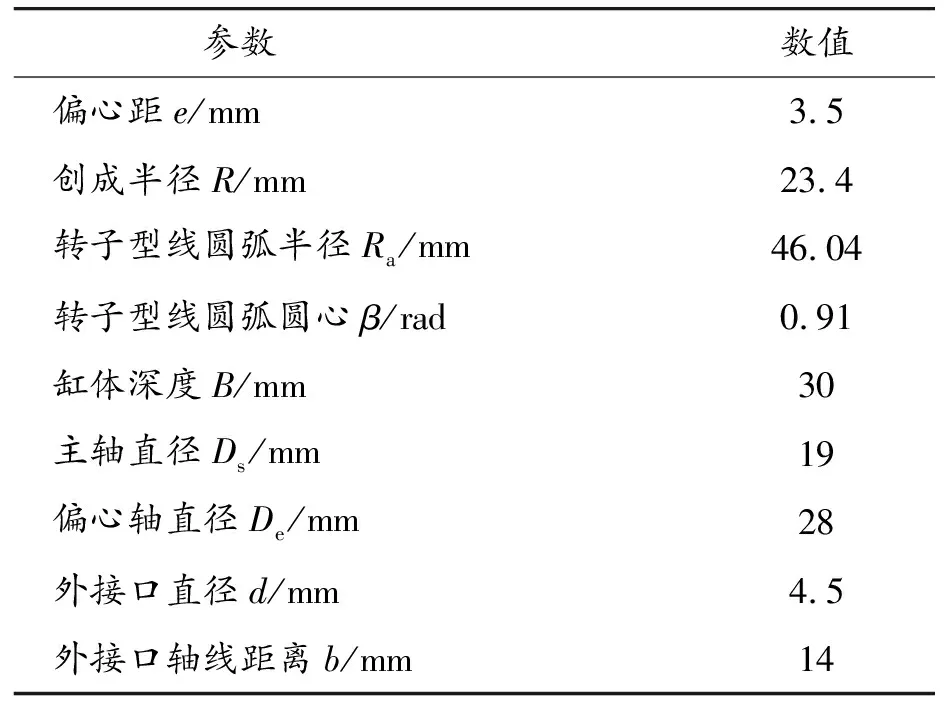
表1 驱动与执行一体式小型汪克尔泵结构参数
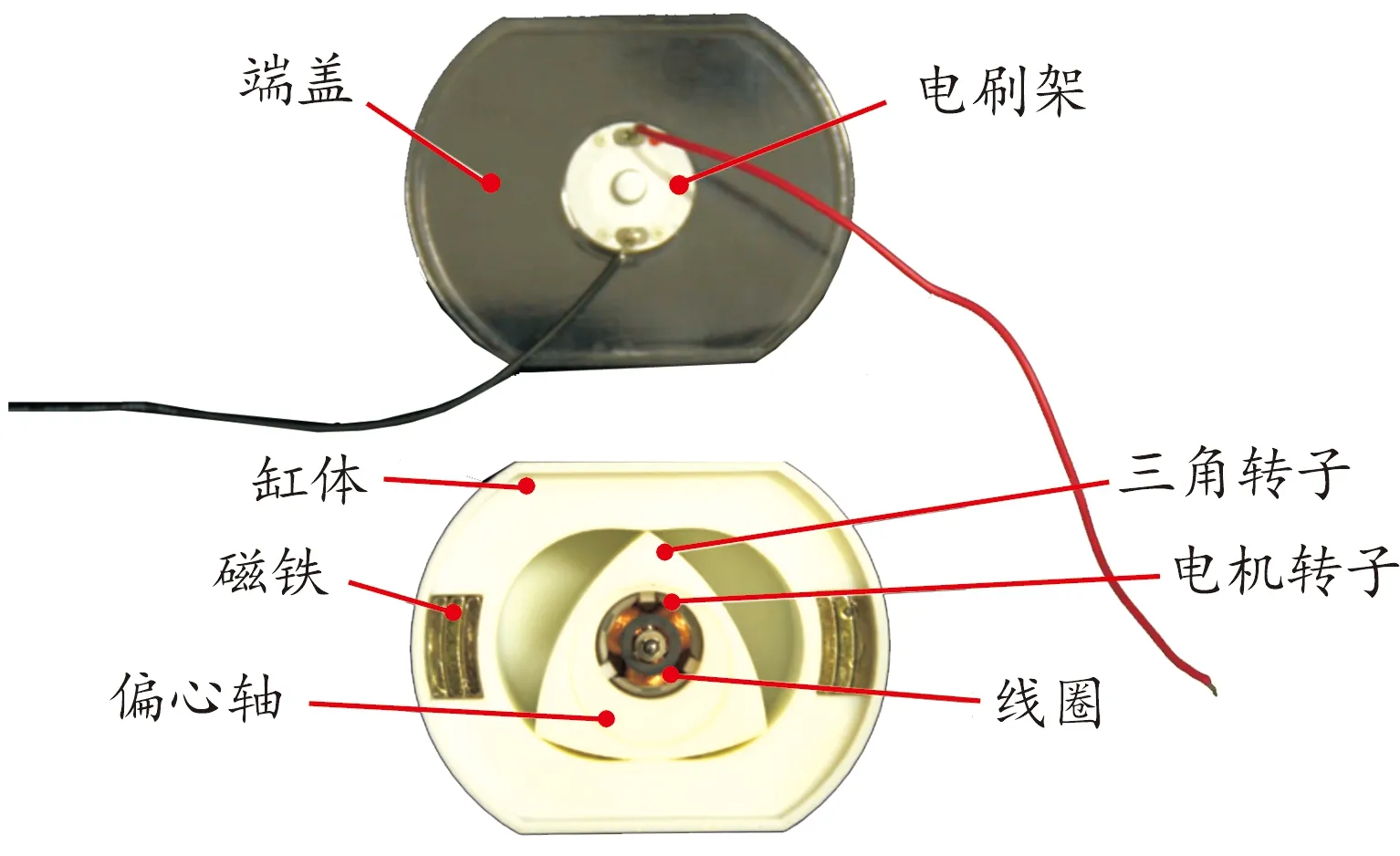
图6 驱动与执行一体式小型汪克尔泵的样机结构示意图
3.2 实验设计
3.2.1工作室流场观测
为了验证泵的泵送功能,观察工作室的流场,进行如图7所示的实验。实验在无风干扰、25 ℃的室温环境中进行,泵送介质为空气。首先将10 g荧光微流子颗粒(直径为1 μm,1.06 g/cm3)加入烧杯中,随后将连接到样机入口的硅胶管插入烧杯的荧光微流子中,另一根连接样机出口的硅胶管插入另一个烧杯中。直流电源(GPC-3060D,Keyence)输出直流电作用到样机的电刷架的电源接口,样机工作,工作室的容积变化将荧光微流子与空气泵送至另一个烧杯中。高速摄像机放置在样机端盖的上方,通过高速摄像机观察观测区域内的荧光微流子运动,从而得出泵的吸入与排出过程的工作室的流场。
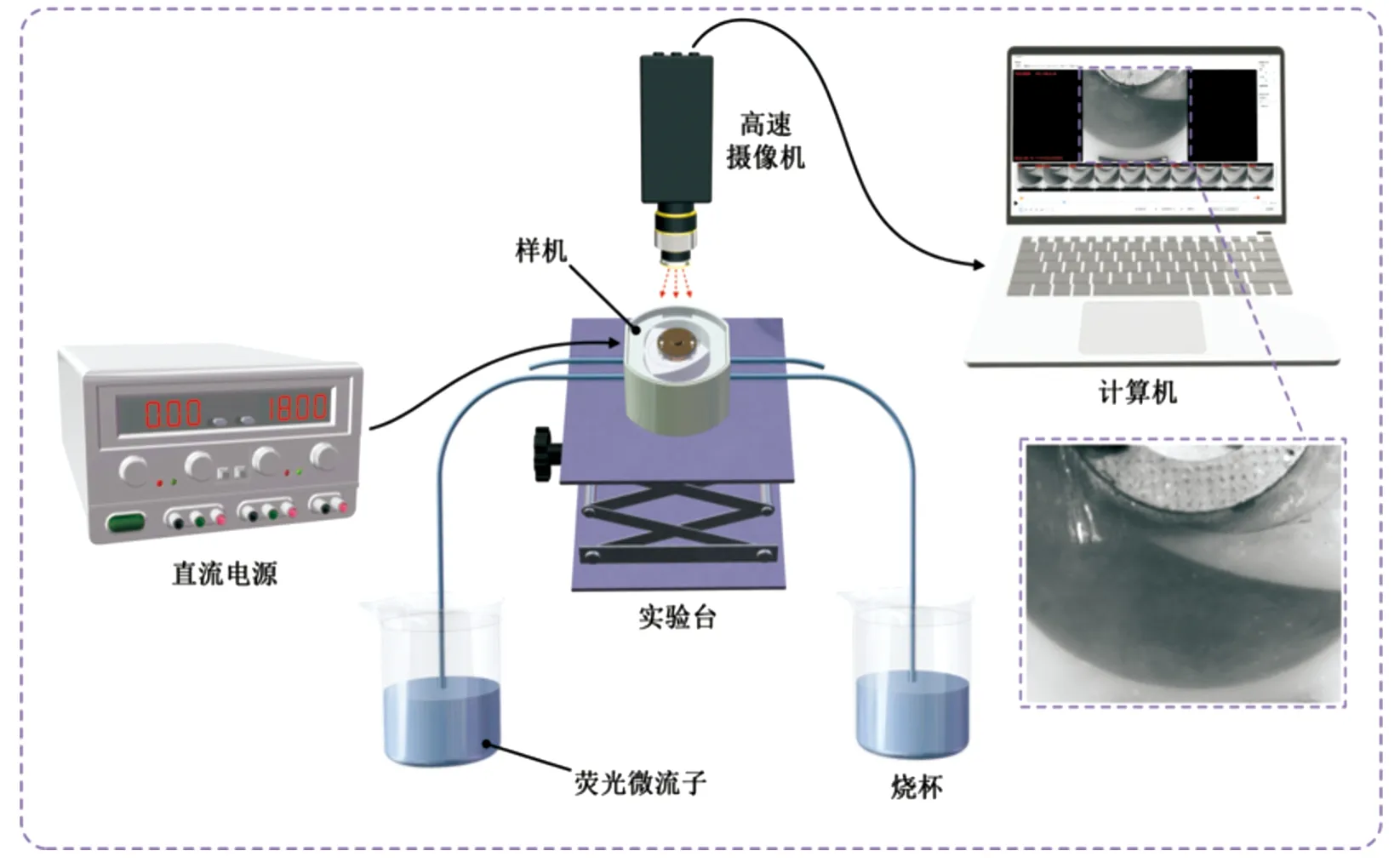
图7 泵内工作室流场观测的实验装置示意图
3.2.2泵送性能测试
如图8、9所示,对驱动与执行一体式小型汪克尔泵进行泵送性能测试。直流电源(GPC-3060D,Keyence)提供直流电的同时检测实际施加的电压。改变放置磁铁块数以改变磁感应强度,运用特斯拉计不同磁铁块数在电机转子处的具体磁感应强度数值。输出转速采用激光转速传感器(LKH020,Keyence)测试并通过数据采集卡传输,泵出口的硅胶管连接流量传感器(MF4003,LangFan)测试输出流量,通过计算机对转速与流量进行监测。此外,设置出口输出压力测试实验,通过动态压力传感器(HELM,HM90)测试泵的出口输出压力。在6~18 V范围电压与11~23 mT范围磁感应强度下,对泵的输出转速、输出流量与输出压力进行测试。

图8 输出转速与输出流量测试的实验装置示意图

图9 输出压力测试的实验装置示意图
4 结果与讨论
4.1 工作室流场观察
图10为1个泵送循环周期中的工作室内微流子的流动情况。
A1—A8为工作室吸入阶段,B1—B8为工作室排出阶段,每隔T/16取1张截图。圆圈表示微流子在泵送周期的不同时间的位置。微流子的运动轨迹和方向用带箭头的曲线表示。在吸入阶段中,靠近进口处缸体壁出现较为明显的涡旋,这是由于吸入的初期工作室容积急剧增大导致存在较大压差,靠近缸壁的边界层微流子沿法线方向的速度梯度很大所形成的。随着工作室容积的增大,工作室其他位置的微流子随转子转动而充满工作室并流向出口,其运动轨迹是向容积增大方向流动。在排出阶段,工作室容积减少,吸入阶段的涡旋逐渐消失。分布在工作室内的微流子随转子转动而流向出口并排出,运动轨迹较为流畅且稳定。可以发现,吸入阶段时工作室内的涡旋较为明显,微流子的流线较为混乱,而排出阶段时工作室流线更为平稳。1个泵送周期后,宏观上可看出微流子从入口流动向出口的过程,验证了驱动与执行一体式小型汪克尔泵的泵送功能。
4.2 泵送性能
图11为驱动与执行一体式小型汪克尔泵在磁感应强度分别为11、16和23 mT时测得的输出转速与输出流量随输入电压变化的情况。
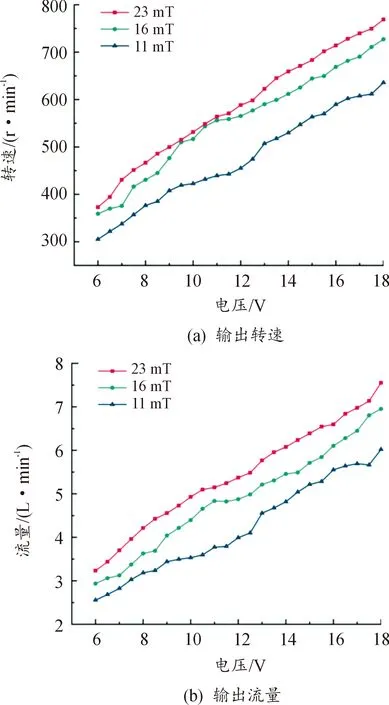
图11 样机在不同输入电压与磁感应强度时输出转速与输出流量
如图11(a)所示,在电压为6~18 V范围内,转速随电压增加而增加,在电压18 V、磁感应强度23 mT时有最大转速,最大转速为768.86 r/min。相同电压下,磁感应强度越大则转速越高。磁感应强度为23 mT时的转速和16 mT时的转速差相比16 mT时转速和11 mT时的转速差更小,与上述理论分析部分一致,磁感应强度增加到一定值时转速的增加趋于平缓,即磁饱和状态。如图11(b)所示,流量的变化特性与三角转子转速的变化特性一致,也是在电压18 V、磁感应强度23 mT时有最大流量,最大流量为7.55 L/min,原因在于转速直接影响工作室“吸入-排出”工作周期循环的快慢,进而影响流量。综上所述,驱动与执行一体式小型汪克尔泵的泵送性能可通过输入电压与磁感应强度调节。
为进一步探究驱动与执行一体式小型汪克尔泵的泵送性能,根据式(34)与图11(b)可以得出其容积效率η为
(35)
式中,Qr为经实验测试得出的实际输出流量。
图12为驱动与执行一体式小型汪克尔泵在磁感应强度分别为11、16和23 mT时测得的容积效率随输入电压变化的情况。容积效率的变化范围在32%~39%,3条容积效率的曲线较为混乱,这可能是由于样泵的装配精度、制造精度不足以及工作时振动等原因造成的误差。对3条折线进行多项式拟合,可以看出容积效率随电压增大而增大,即随着转速的升高,流量的损失比例减少,在电压为18V、磁感应强度为23 mT时达到最大值38.47%。

图12 样机在不同输入电压与磁感应强度下的容积效率
图13(a)中黑线为电压18 V时动态压力传感器在2个出口处测量到的瞬时压力变化曲线,红线为经过傅里叶变换(FFT)滤波处理后得到的较为平滑的拟合曲线。该曲线与时间关系为正弦谐波曲线,可近似反映与出口相连的泵送循环过程的压力变化情况,压力增大时即为工作室容积减少,压力减少时即为工作室容积增加。对拟合曲线的最高压力与最低压力作差得到压力幅值ΔP,继而得到图13(b)在磁感应强度分别为11、16和23 mT时的输出压力幅值随输入电压改变情况。可以看出,压力幅值随输入电压的增加呈上升趋势,在电压18 V、磁感应强度23 mT下有最大压力幅值7 kPa,原因是随着电压升高,转速增大,工作室容积变化的速率增大,造成压力幅值增加。综合分析驱动与执行一体式小型汪克尔泵的泵送性能曲线,转速-电压曲线、流量-电压曲线和压力幅值-电压曲线三者具有较为稳定的一致性。
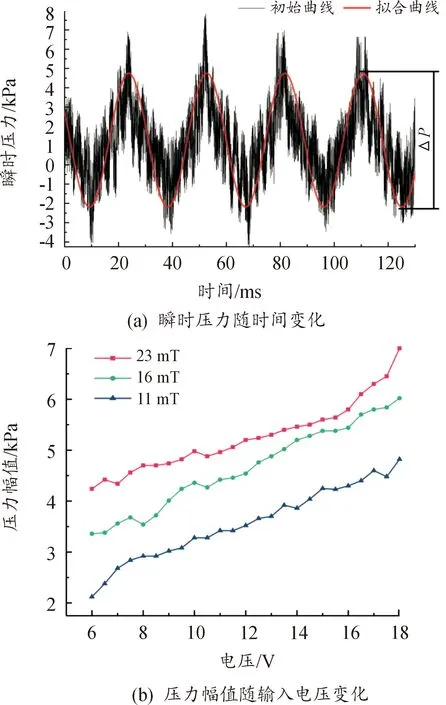
图13 样机出口的输出压力
5 结论
1) 驱动与执行一体式小型汪克尔泵可将驱动组件集成到执行组件中,具有泵送功能的同时可有效减小汪克尔泵的体积,减少传动路径上的损耗。研究了汪克尔泵的缸体型线与转子型线的数学模型,转子设计时用简单圆弧曲线替代缸体型线包络线的复杂曲线,能简化加工过程,有效推进汪克尔泵小型化集成化的进程。
2) 分析研究了泵的泵送性能,建立了三角转子的动力学模型,以及输出转速与负载、电机转子参数、磁感应强度的关系。通过对工作室容积变化的分析,得出该泵的输出流量的表达式。
3) 实验测量了在磁感应强度分别为11、16和23 mT时输出转速、输出流量和输出压力随输入电压的变化情况。在输入电压18 V、磁感应强度23 mT时有最大转速768.86 r/min,最大流量7.55 L/min,最大压力幅值7 kPa。分析得出转速-电压曲线、流量-电压曲线和压力幅值-电压曲线三者具有较为稳定的一致性。计算得出容积效率随电压的变化范围在29%~38%,其大致趋势为容积效率随电压增加而增加。
