基于双强度折减幅值加权法的公路边坡稳定性研究

武博强，李 博

(中交第一公路勘察设计研究院有限公司，陕西 西安 710065)

0 引言

双强度折减法(DRM)是基于岩土体黏聚力与内摩擦角发挥作用的先后及衰减速度的差异，将对应黏聚力及内摩擦角的双折减系数代替传统的单一折减系数(SRM)，DRM法无论从原理角度还是实际工程角度出发，都能更准确地分析边坡的稳定性情况。目前双强度折减法的研究成果主要集中于3方面，首先是分析单独折减c值与φ值的折减系数间的关系，确定双折减系数比K值，并采用传统方法进行比较。唐芬等[1]基于室内试验结果对边坡的渐进破坏机理进行了分析，并推导了基于传统条分法的强度折减公式，文中采用的K值是对应c值与φ值的单独折减系数的比值，郭建军[2]以顺层岩质边坡为研究对象，认为K值等于对应c值与φ值的单独折减系数增幅值的比值，从原理上来看采用单独折减系数的比值作为K值更为合理；其次是双强度折减法边坡稳定系数的确定，唐芬等[3]曾对双强度折减法最终折减系数公式进行讨论，将双强度折减系数的平均值作为最终折减系数，本研究认为，平均值虽然应用方便但其误差较大，且无理论及实践支撑，偏安全和偏危险均有可能。朱彦鹏、杨校辉等[4-5]以碎石土高填方边坡为研究对象，基于强度储备面积，定义双强度折减法最终折减系数等于两个单强度折减系数乘积的平方根，但该公式从第1步推导时就已经默认其最终折减系数的平方值等于双强度折减系数的乘积，理论依据相对不足。最后是坡形要素的影响分析，国内学者普遍采用1级均质黏性土边坡模型进行研究，抗剪强度参数固定，对同一组抗剪强度数据进行折减分析可以简便快速的分析黏聚力和内摩擦角间的相互关系，多名学者[6-7]基于均质黏性土边坡总结出最终折减系数经验公式，但这种折减模型适应性较差，一是由于实际工程中岩土层的多变，边坡坡度根据岩土体种类采用不同的边坡坡率，均质边坡的情况几乎难以遇到；二是以极限平衡法为准确值建立公式模型，公式模型本身就有误差，极限平衡法在分析没有明确滑动面的边坡时只能提前指定多种滑动面进行搜索计算，而这也是强度折减法在高边坡计算上优于极限平衡法的地方[8]，因此如果仍以极限平衡法作为准确值反推公式模型，成果的应用价值较低。

基于双强度折减法的研究现状，本研究引申了两个需进一步研究的内容，首先是双强度折减法在实际公路工程中多种岩土层结构边坡模型的应用；其次是寻找一种适用于实际工程且准确度高的边坡稳定系数的确定方法。

本研究以内蒙古某高速公路工程某多层岩土体高边坡为研究对象建立相应的边坡模型进行折减分析，提出了基于内摩擦角及黏聚力折减速率和对边坡稳定系数影响程度确定双强度折减边坡稳定系数的新思路，并与统一折减法及极限平衡法进行比较，旨在为双强度折减法在实际公路工程的应用提供一些参考。

1 双强度折减法在实际工程中的研究思路

双强度折减法的原理是根据岩土体的c值与φ值的单独折减系数得到两者的关系式，再以c值或φ值的单独折减系数为未知数代入强度折减公式中进行迭代计算，边坡平面应变模型相关如式(1)～(2)所示：

(1)

(2)

式中，Fs为边坡稳定系数；τ为岩土体允许抗剪强度；c为岩土体黏聚力；φ为土体内摩擦角；l为潜在滑面长度；SRF1为黏聚力单强度折减系数；SRF2为内摩擦角单强度折减系数。

确定双强度折减边坡稳定系数的核心是要明确最终单强度稳定系数的关系，得到单强度稳定系数前需要单独对c值和φ值进行折减计算，得到单独折减系数后两个折减系数的关系可用式(3)中的比值K来表示，并将单强度稳定系数通过式(3)～(4)转换为单未知数求解：

(3)

(4)

式中，Fs1为黏聚力单强度稳定系数；Fs2为内摩擦角单强度稳定系数；K为折减系数比。

而最终边坡稳定系数Fs是由两个单强度稳定系数构成的，其潜在关系可以用单强度折减系数的增幅比来表示，为分析该内在关系做出如下假设：假设黏聚力的折减幅度大于内摩擦角，那么这同时说明黏聚力对边坡稳定系数的敏感度小于内摩擦角，对稳定系数的贡献度与折减幅度呈负相关关系，即折减系数大，对边坡稳定系数的敏感度较小，贡献度也较小。因此本研究假设可通过黏聚力和内摩擦角的折减幅值加权来得到双强度折减边坡稳定系数如式(5)所示：

(5)

综上，双强度折减法在实际工程中的研究思路可分为以下5个内容：

(1)研究区典型边坡的建立及抗剪强度参数取值

选取研究区典型深挖路堑高边坡，根据地质勘察及室内试验结果对边坡土层抗剪强度参数进行综合取值，根据《公路路基设计规范》(JTG D30—2015)[9]制定合理边坡坡率后建立边坡模型。

(2)求解单独折减系数

首先对边坡模型的c值进行折减，φ值不折减；然后对φ值进行折减，c值不折减，分别得到相应的单独折减系数SRF1与SRF2。

(3)求解双强度折减系数比值

根据式(3)求解不同土体边坡模型的双强度折减系数增幅比值K。

(4)求解最终稳定系数

根据式(4)，以内摩擦角单强度稳定系数作为未知数进行边坡强度折减计算，得到内摩擦角和黏聚力的单强度稳定系数，根据式(5)对单强度稳定系数加权计算求得最终边坡稳定系数。

(5)与国内学者普遍采用的平均值法、平方根法进行对比，验证本方法的适用性[10-14]。

2 实例分析

2.1 研究区概述及边坡计算模型的建立

内蒙古某高速公路位于鄂尔多斯准格尔旗境内，研究区以山区地貌为主，沿线约有45处深挖路堑边坡及50处高填方边坡，研究区岩土体分布多元，主要结构为上覆黄土状粉土，下覆全风化、强风化泥岩或砂岩，底部基岩为中风化砂岩。根据规范建议及地方经验，上覆黄土状粉土及全风化、强风化泥岩砂岩层边坡坡率采用1∶1，中风化砂岩层边坡坡率采用1∶0.75。

数值模型的建立对数值分析的影响至关重要，数值模型主要分为三维实体模型及假三维/二维模型，由于最终安全系数需要与极限平衡法及统一强度折减法进行校核，因此选取3种方法均适用的假三维/二维模型。边坡模型的尺寸效应参考唐芬等[1]的边坡模型，各方向长度均延伸一个坡高，同时考虑模型收敛性，网格采用1 m×1 m四边形网格，选取研究区K2+550-K3+150挖方段典型高边坡作为研究对象进行分析，建立模型如图1所示。

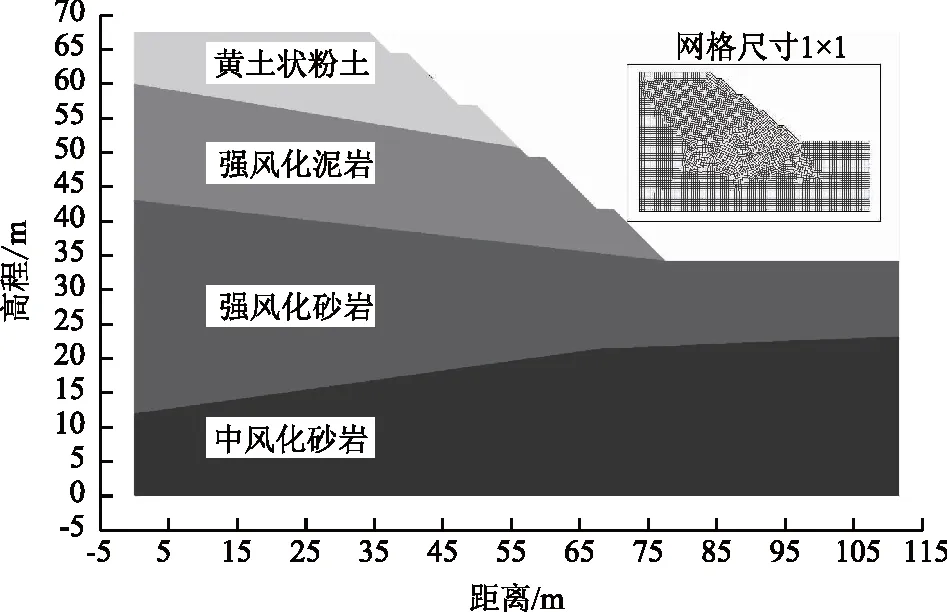
图1 边坡计算模型Fig.1 Calculation model of slope

根据地质勘察资料，研究区主要岩土体物理力学参数见表1。

2.2 单强度折减及结果分析

单强度及双强度折减法均通过FLAC3D软件的FISH语言平台进行编写来实现，命令流主要编写原则如下：

(1)对边坡各层岩土体的密度、弹性模量、泊松比采用软件默认计算方法进行定义。

(2)黏聚力单强度折减时，令内摩擦角φ1值等于φ/1，即在边坡计算时保持内摩擦角无变化，令黏聚力c1值等于c/SRF1，对岩土体赋予摩尔库伦本构模型后，对黏聚力赋值c1后进行单强度折减计算，内摩擦角单强度折减时原理同黏聚力。

(3)为更快得到计算结果，稳定系数求解采用二分法，即在命令流中确定稳定系数分为最大值为K1最小值为K2的两个值，令两值差值为0.05时循环停止，此时求得单强度稳定系数SRF1，数值大小等于K1与K2的平均数。

首先对各边坡模型进行黏聚力强度折减，K1取值0.5，K2取值4.1，共折减循环6次，黏聚力随折减系数变化曲线如图2所示。

图2 黏聚力随折减系数变化曲线Fig.2 Curves of cohesion forces varying with reduction coefficients

从图3中可以看出黏聚力单强度折减程度较大，最终需要折减至2.792边坡才会发生临界破坏，破坏时最大剪应变增量为0.014 9，潜在滑动面为深层滑动，下部边坡位移较大，折减破坏最大位移为8.86 cm。破坏时黄土状粉土黏聚力为5.372 kPa，强风化泥岩及中风化砂岩黏聚力为8.954 kPa，强风化砂岩黏聚力为5.730 3 kPa。

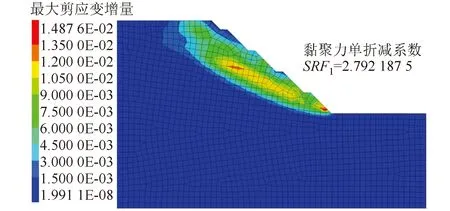
图3 黏聚力单折减计算结果Fig.3 Calculation result of single reduction of cohesive forces

然后对各边坡模型进行内摩擦角强度折减，K1取值0.5，K2取值2.0，共折减循环8次，内摩擦角随折减系数变化曲线如图4所示。

图4 内摩擦角随折减系数变化曲线Fig.4 Curves of internal friction angles varying with reduction coefficients

从图5中可以看出内摩擦角单强度折减系数为1.453 9，较黏聚力小1.338，破坏时最大剪应变增量为0.105(见图5)，较黏聚力单独折减时形成了更为明显的剪应变贯通区域，且折减破坏时X向最大位移值为26.5 cm，明显大于黏聚力单独折减破坏时相应位移值，这说明内摩擦角对边坡稳定系数的影响更大，较黏聚力对边坡稳定性更为敏感，破坏时黄土状粉土内摩擦角为20.63°，强风化泥岩内摩擦角为19.26°，强风化砂岩内摩擦角为24.07°，中风化砂岩内摩擦角为27.51°。

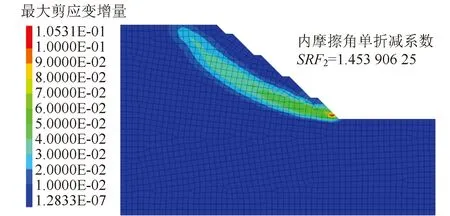
图5 内摩擦角单折减计算结果Fig.5 Calculation result of single reduction of internal friction angle

2.3 双强度折减及结果分析

根据单强度折减结果采用式(3)进行计算得到折减系数比K值为1.920 5，将内摩擦角作为未知数代入边坡模型中进行折减系数，令K1值为0.5，K2值为2.0，共计折减8次，得到内摩擦角最终单强度稳定系数为1.08，黏聚力最终单强度稳定系数为2.074。K1，K2与Fs2折减关系曲线如图6所示，折减过程为K1与K2和的平均值折减—K2取前一次计算结果折减、K1不变—K1连续折减2次，K2不变—K2连续折减3次，K1不变—K1取前一次计算结果折减求得最终值。

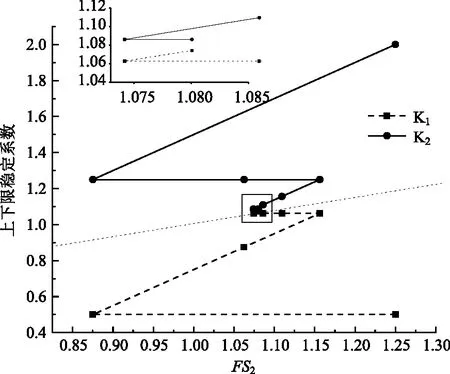
图6 K1，K2与Fs2折减关系曲线Fig.6 Reduction curves of FS2 with K1 and K2

破坏时最大剪应变增量为0.017(见图7)，边坡模型内摩擦角及黏聚力双强度折减结果如图8所示，折减后黄土状粉土、强风化泥岩、强风化砂岩及

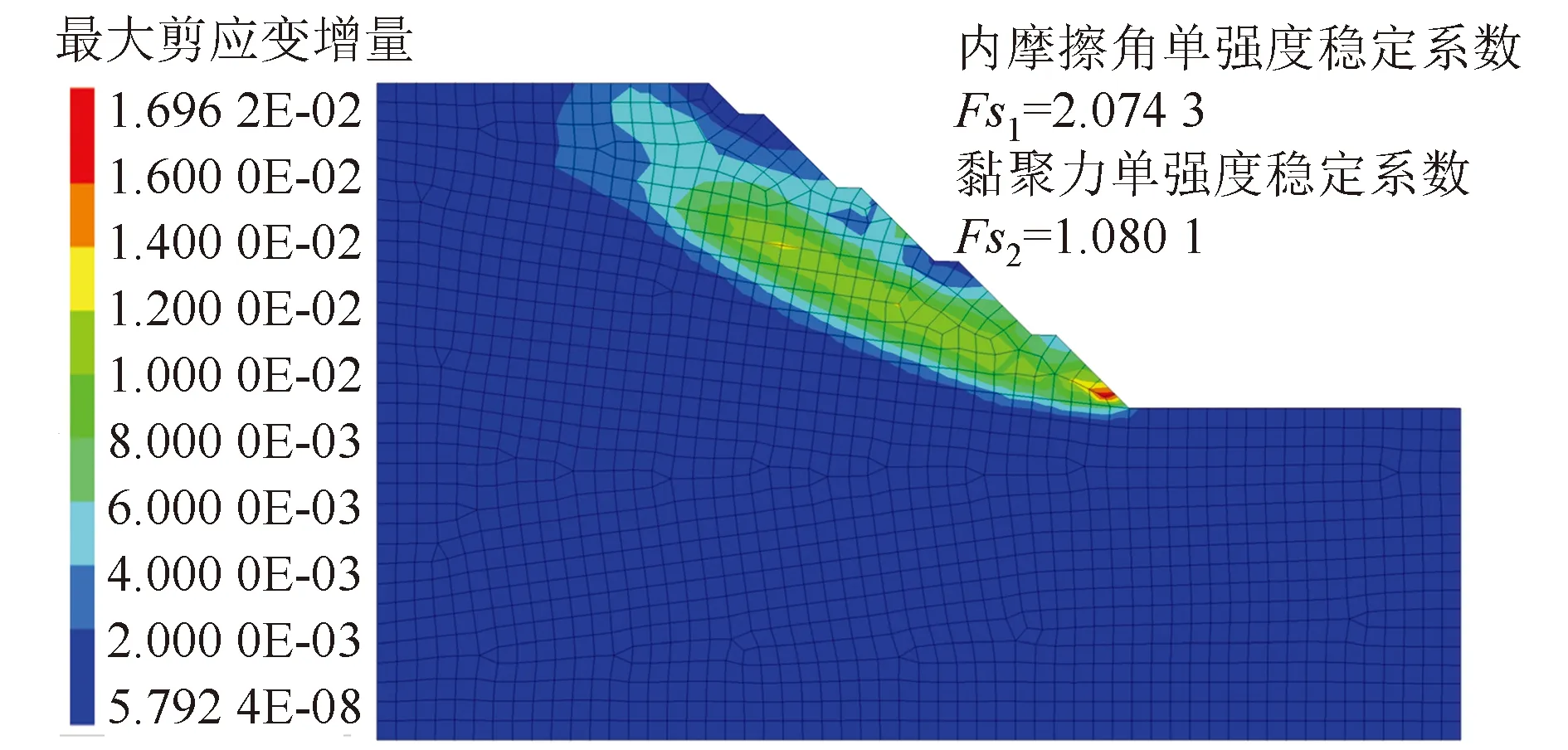
图7 双强度折减计算结果Fig.7 Calculation result of double reduction

图8 双强度最终折减系数Fig.8 Final reduction coefficients of double strength

中风化砂岩内摩擦角依次为28.26°，26.33°，33.1°和37.99°，对应折减黏聚力依次为7.271，12.05，7.756，12.05 kPa。

2.4 最终边坡稳定系数

黏聚力和内摩擦角的单强度最终稳定系数分别为2.074与1.08，黏聚力的折减幅值约为179.22%，内摩擦角的折减幅值约为45.39%，根据式(5)建立最终边坡稳定系数模型(折减幅值加权)，计算结果为1.281，为证明该方法的优越性分别与极限平衡法、统一强度折减法及其他双强度最终边坡稳定系数确定方法(平均值法、平方根法及文献[7]中的经验公式法)进行对比[15-19]，对比结果见表2。

表2 各方法计算结果对比Tab.2 Comparison of calculation results with different methods

根据研究边坡的岩土体特性选取了极限平衡法中的毕肖普法和摩根斯坦法进行比较，其中毕肖普法计算结果为1.253，摩根斯坦法为1.247，采用统一强度折减法(SRM)的计算结果为1.230，是所有方法中计算结果最小的一组，可见统一强度折减法由于采用了同一个折减系数，所得结果偏安全，而其他学者总结出的双强度折减法最终边坡稳定系数结果均较大，平均值法为1.577，而平方根法为1.50，这说明这两种方法并不适用于岩土体多样的边坡工程，实际工程应用相对较差。

2.5 方法的普遍适用性研究

在文献[3]中，唐芬等[1]折减c值后给定不同的K值进行试算，最终与极限平衡法计算结果进行对比，取误差在2%范围内的K值时的双强度稳定系数平均值作为最终边坡稳定系数，该方法虽然可以很清晰的推导出双强度折减系数的关系，但需进行大量的试算，先假定多个K值，主观性较强。为更清晰、直观地体现基于折减幅值加权的双强度折减法的优势及普遍适用性，选取澳大利亚ACADS协会的一个均质边坡算例做进一步的分析，该算例强度参数共有3组，相关计算参数及极限平衡法计算结果如图9所示。

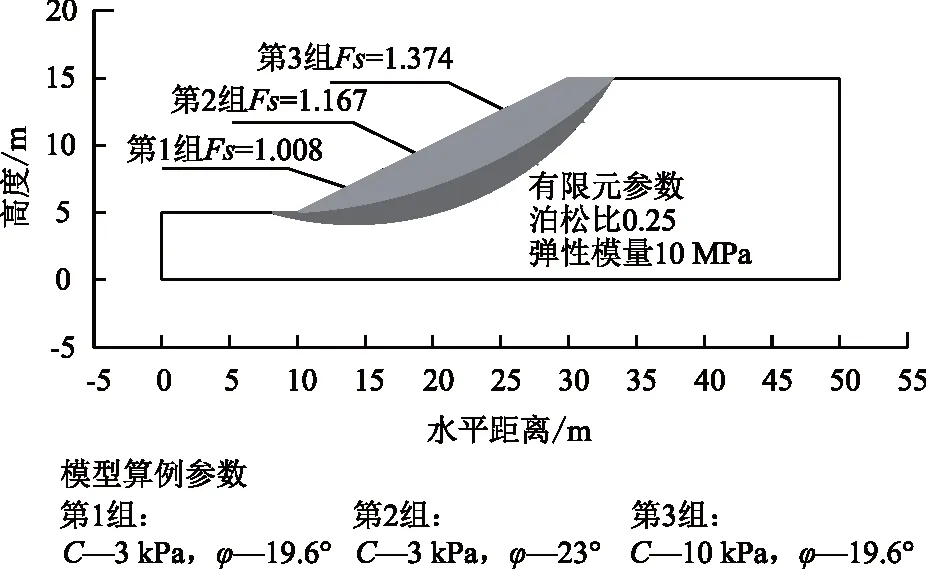
图9 均质边坡算例模型尺寸及相关参数Fig.9 Homogeneous slope study model size and related parameters

采用双强度折减幅值加权法对该算例3组参数进行计算，计算步骤见表3，得到的边坡最终安全系数与平均值法、平方根法、公式法等双强度折减法进行对比，并采用极限平衡法作为校核，结果如表4所示，采用折减幅值加权得到的双强度折减边坡稳定系数计算结果与极限平衡法最为接近，且每次离散性均很小，更适用于实际工程的计算分析。

表3 双强度折减法(折减幅值加权法)计算涉及数据Tab.3 Calculation data involving DRM(reduction method with amplitude weighting)

表4 各方法计算结果对比Tab.4 Comparison of calculation results with different methods

3 结论

基于双强度折减法的研究现状，提出了折减幅值加权法来确定边坡最终稳定系数的思路，在以下方面取得了一些进展：

(1)基于实际公路工程，确定了详细的强度折减法的研究思路流程，选取高边坡发育的研究区建立边坡模型，对多岩土层高边坡进行了稳定性分析，与多种方法对比后发现，基于折减幅值加权的双强度折减法来确定边坡最终稳定系数更适用于实际工程中潜在滑动面不确定的高边坡，与极限平衡法计算结果相差较小。

(2)黏聚力、内摩擦角折减程度与敏感度成负相关的关系，基于此观点推导出了基于折减幅值加权的双强度折减法确定边坡最终稳定系数的公式模型，并通过实际工程案例及既有文献典型案例从多土层高边坡和均质边坡多角度证明了该方法的可行性和普遍适用性。

(3)双强度折减法除稳定系数外可提供x向位移、剪应变增量是否贯通等判据，为边坡稳定性评价提供了多方面的判据；由于极限平衡法提前假定潜在滑动面，无法得出极限平衡法与双强度折减法计算结果哪种方法更优的结论，建议结合滑动面更为确定的滑坡进一步深入研究。