车载控制力矩陀螺动力学特性研究

石晓辉,王 林,葛帅帅

(重庆理工大学 车辆工程学院,重庆 400054)

0 引言

控制力矩陀螺(control moment gyro,CMG)具有主动回正力矩的能力,且力矩可放大,可控效果较好。因此,CMG技术在空间站、卫星与航天飞行器、两轮平衡车等需要主动姿态调整与平衡控制的领域得到重点研究和广泛运用[1]。在资源匮乏与紧张的大环境之中,将单框架控制力矩陀螺(single frame moment gyro,SGCMG)技术应用到自平衡两轮汽车领域,以此来提高道路与车辆的使用效率,同时实现某些特殊工况与场景的运用,这是非常有必要和有价值的研究[2]。单框架控制力矩陀螺(SGCMG)系统作为两轮自平衡车平衡系统的核心,其机械部分主要包括了储存惯量的转子和起支撑作用的框架与轴承等关键部件。其中转子的转速会受到耦合支撑系统刚度的影响,导致转子在实际运行中达不到最高转速,从而影响自平衡两轮车在极端工况下的平衡力矩输出不足,严重可能会导致整车平衡系统失控。因此,通过对SGCMG耦合柔性支撑系统进行动力学固有特性的分析与评估,探究转子系统模态频率随惯性转速的变化规律;系统临界转速对轴承径向刚度变化的敏感程度,找出轴承径向刚度的合理阈值;同时探究偏心质量引起的不平衡响应在不同方向上的振动幅值大小和稳态响应下框架与转子的振动特性。这一系列工作关系到两轮车载力矩陀螺最大性能是否得到发挥,为后续优化与改进提供参考。

控制力矩陀螺(CMG)一直是国内外研究的重点技术之一,已经在航空航天、航海、国防军事等关键领域得到了运用。国内外学者也对SGCMG做了相关的研究,例如:冯洪伟等[3]通过有限元仿真软件对陀螺整体和组合结构进行了模态分析,并将仿真结果与实验对比,得出转子轴弯曲模态是系统的主要模态的结论,揭示了影响系统稳定性的主要因素。王帅等[4]对控制力矩陀螺建立了系统动力学方程,基于复模态理论,构造了实数域上的伪模态矩阵,实现了系统动力学方程的解耦,且验证了使用伪模态矩阵进行方程解耦的可行性及控制的有效性。代彦宾等[5]建立了控制力矩陀螺高速转子的有限元模型,研究了高速转子一阶临界转速受旋转质量、辅板角度、安装跨度、安装预紧力的影响规律。黄志来等[6]建立了能在全部可行域中进行输出特性解析的单框架控制力矩陀螺力矩输出模型,通过定义输出输入力矩比和输出力矩利用率2个参数研究了SGCMG输出特性对控制效果的影响,同时验证了单框架控制力矩陀螺始终具有力矩放大效应和高效的力矩利用率这一输出特性。Lappas等[7]和Alcorn等[8]基于SGCMG转子高转速与框架低转速的假设,通过借鉴反作用轮原理分析了单框架力矩陀螺输出特性中的力矩放大效应。郎跃东等[9]对控制力矩陀螺框架结构刚度与振动特性进行了分析,研究了其在大载荷作用下的应力应变,在满足结构刚度与控制精度的要求下进行了相应的优化设计,有效改善了框架的振动特性。Xu等[10]研究了控制力矩陀螺的微振,使用拉格朗日方程建立控制力矩陀螺隔振耦合系统的动力学模型,通过此模型分析了框架旋转与转子转动的耦合关系,得到了飞轮转速、隔振器刚度及框架转动对控制力矩陀螺输出振动的影响规律。刘晓东等[11]建立了控制力矩陀螺的三维几何模型,通过有限元软件对其模型进行了动力学分析,研究了单框架力矩陀螺的模态、频率响应及随机响应等动力学特性,验证了结构的可靠性,为优化提供了理论参考。董晓阳等[12]以结构基频/质量比作为优化目标值,对控制力矩陀螺框架进行动力学分析,在有限元软件中通过复合材料铺层设计进行框架结构的几何优化设计,分析结果表明优化后的陀螺框架具有更高的结构效率和可靠性。林鲁超等[13]对单框架控制力矩陀螺转子转速的动态与稳态性能进行了相关研究,提出了一种引入干扰力矩补偿控制的方法,实现了控制力矩陀螺转子的稳速控制,有效抑制了转子的转速波动,提高了系统的可靠性。

综合上述分析发现,目前对控制力矩陀螺的研究主要集中于模态、临界转速、输出特性和结构可靠性等方面,很少考虑柔性体支撑框架与转子轴承刚度耦合因素对系统响应的影响,且对两轮车载单框架控制力矩陀螺的动力学行为基础研究较不足。因此,本文针对某特定两轮车载单框架控制力矩陀螺,构建框架-轴承-转子耦合系统的有限元分析模型。首先,探究耦合系统模态随惯性转速变化的规律及转子轴承径向刚度对系统临界转速的影响。其次,通过研究SGCMG转子在特定偏心质量下的系统不平衡响应,验证临界转速分析的准确性。最后,进一步研究耦合系统框架与转子在稳态响应下振动特性。根据分析得到的结论,为SGCMG后续的优化设计及工程运用提供参考依据。

1 理论基础与有限元模型

1.1 框架-轴承-转子耦合系统动力学模型

考虑框架与轴承柔性支撑刚度的影响,把系统离散化后再通过数学方法手段进行处理,得到相应有限元模型的运动微分方程。离散化模型的优点在于可以对复杂结构系统进行数值求解,得到相对精确的结果,同时可以考虑陀螺效应、自身转动惯量、外阻与结构内阻等因素的影响[14]。

将力矩陀螺框架-轴承-转子耦合系统离散成如图1所示的有限单元系统,每个单元运动方程都有所不同,可以得到每个单元的阻尼矩阵、刚度矩阵、惯性矩阵和外载向量,将每个单元的运动方程重新组装一起,即可得到系统的运动微分方程。

图1 有限元离散系统

对于N自由度的框架-轴承-转子耦合系统,可以得到运动微分方程如式(1)

(1)

式中:M是系统的质量矩阵;U={xi,yi,zi,θxi,θyi,θzi}T,i=1,2,…,N,是广义位移量;C是由Rayleigh耗散函数得出的对称N阶阻尼矩阵;G是由陀螺力矩产生的动能得出的反对称N阶陀螺矩阵;K是由势能得出的刚度矩阵和轴承与框架支撑贡献的刚度矩阵组合而成的广义刚度矩阵;F表示外载荷的N阶一维向量。

1.2 框架-轴承-转子耦合系统有限元模型

控制力矩陀螺作为机械系统调整姿态的核心部件如图2所示,属于一个复杂的装配体系统,加上复杂工作环境与恶劣工作条件的影响,该系统运行过程涉及到多物理场耦合现象。但在分析系统固有属性时,只考虑关键部件的影响,忽略螺栓孔、加工倒角和转子电机框架次要因素,得到如图3所示的框架-轴承-转子耦合简化模型。

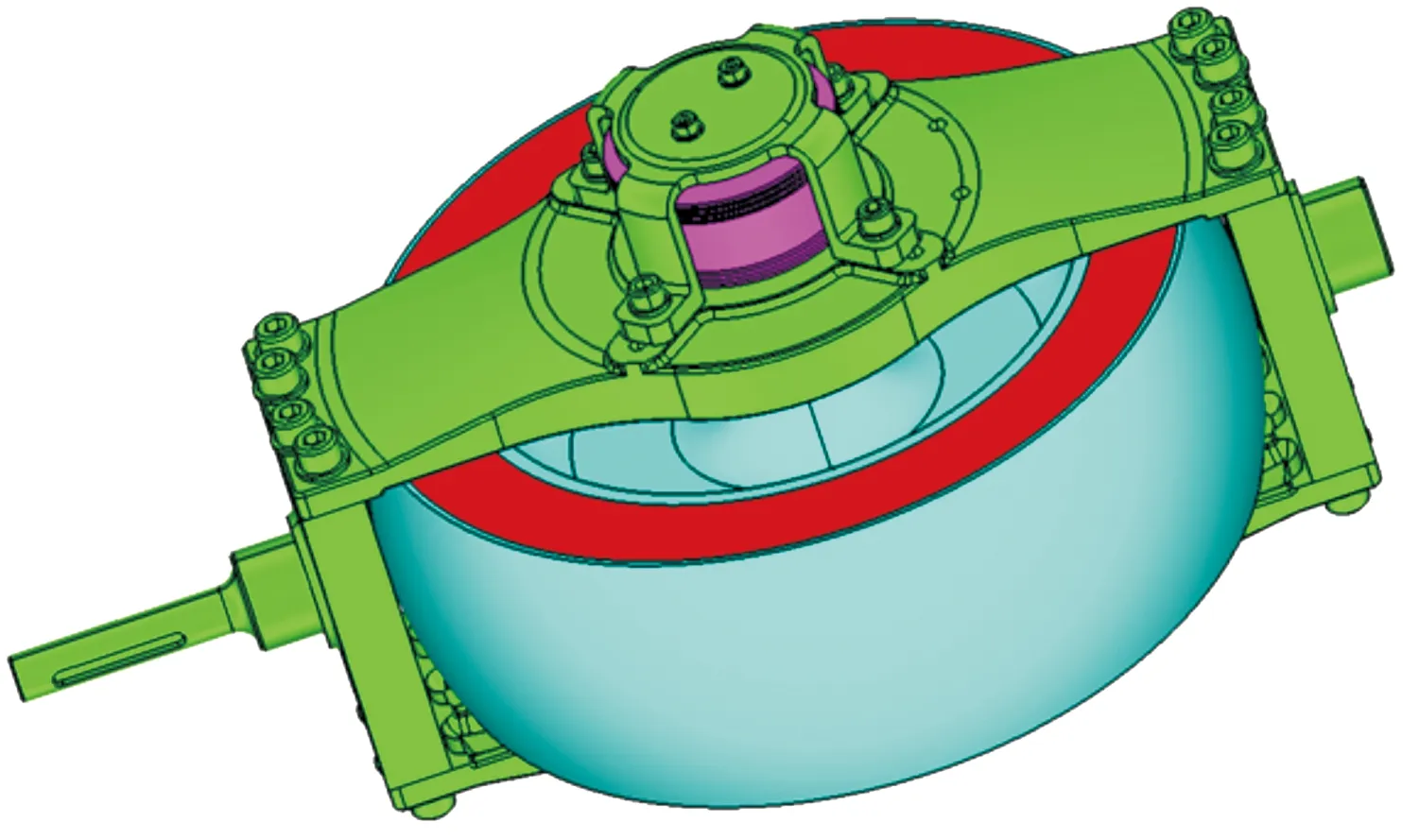
图2 CMG转子系统原始模型

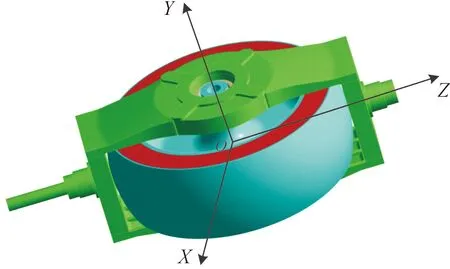
图3 CMG转子系统简化模型

为了得到较为理想的离散单元系统,提高分析的精度,节约计算资源,在Hypermesh中对简化后的模型进行全六面体网格系统的构建。图4为部件网格与整体网格模型示意图,其网格质量统计如表1所示。

表1 各部件网格质量统计

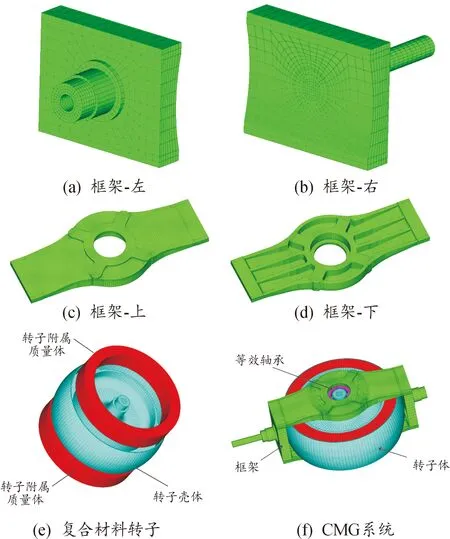
图4 有限元网格模型

系统各个部件的材料分别为:框架用7075铝合金、转子体用45钢、转子芯用铅,具体参数如表2所示。

表2 各部件材料参数

在Hypermesh中创建各部件系统的连接关系,通过共节点的方式实现复合材料转子壳与转子芯之间的连接,使用绑定约束模拟上下框架支撑架与左右框架支撑架间的螺栓连接,使用弹簧单元spring模拟转子轴承的径向支撑刚度,通过转动副MPC184单元模拟轴承与转子间的转动效果。最后将创建好的有限元分析模型导入Ansys中进行后续的分析。

2 耦合系统固有属性分析

系统的模态频率与离散单元数量有关,具有成千上万阶模态,但是对于结构运动起主要影响作用的是低阶模态,因此在以下研究中只提取除去刚体模态的前五阶模态进行分析。在转子系统的设计与分析中,动力学特性都与临界转速相关,所以临界转速的计算是必不可少的环节。在式(1)动力学方程基础上,去掉外载向量将方程变成齐次式为:

MU+(C+G)U+KU=0

(2)

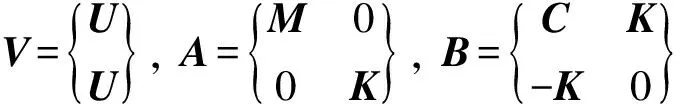
可将式(2)变为:

(3)

令V=V0evξ,代入式(3)中可得:

(Av+B)V0=0

(4)

将上述问题转化为求解标准特征值问题,为:

(D+vI)V0=0

(5)

由式(5)可求得特征值和特征向量,其中虚部为转子的临界转速。

2.1 框架-转子耦合系统固有属性分析

在考虑陀螺效应的情况下,将耦合系统弹簧单元刚度设置无穷大,得到框架-转子耦合系统。在Ansys中设置0～20阶模态频率,在每一阶模态频率下等间距施加0～12 000 r/min的7组惯性转速,得到框架-转子耦合系统的各阶频率与转速数据如表3所示。考虑陀螺效应后,第二阶模态频率随着惯性转速升高而降低,第四阶模态频率随着惯性转速升高而增大,第三、五、六阶模态频率随着惯性转速变化不明显。

表3 框架-转子系统惯性转速与模态数据

将表3中数据以惯性转速为横坐标,以模态频率为纵坐标绘制成图5所示的框架-转子坎贝尔图。图中从原点引出一倍频激励直线,一倍频线与各阶模态曲线交点的横坐标值为所求的临界转速,纵坐标值为该临界转速所对应的系统固有频率。

图5 框架-转子系统坎贝尔图

从图5可以看出,一倍频激励直线与二阶、三阶模态频率曲线的交点的横坐标值分别为系统对应的前两阶临界转速:一阶临界转速为5 984 r/min,二阶临界转速为11 855 r/min。图中FW为正进动,BW为反进动。由于在实际工程中,只有正进动频率才会引发系统的不稳定,因此只关注一倍频线与正进动曲线的交点。

转子框架耦合系统中,一阶临界转速与二阶临界转速所对应的模态振型分别如图6与图7所示。

图6 一阶临界转速的模态振型

模态振型结合模态质量参与系数可以定量地看出,一阶临界转速对应的模态振型主要在Z方向发生了平动振动,这可能会对框架轴承的径向支撑产生过载现象,同时引起转子体轴向的窜动。二阶临界转速对应的模态振型主要是框架与转子在Y方向发生了扭曲振动,可能会导致转子轴承径向过载或框架变形过大等现象。

2.2 框架-轴承-转子耦合系统固有属性分析

根据本款车载控制力矩陀螺转子转速与支撑要求,选型NSK6306轴承作为转子轴承。通过查表得到该轴承径向刚度为240.4 kN/mm。故在耦合系统中将等效轴承径向支撑的弹簧刚度设置为240 kN/mm为例进行分析,得到框架-轴承-转子系统在不同惯性转速下的各阶频率数据如表4所示。

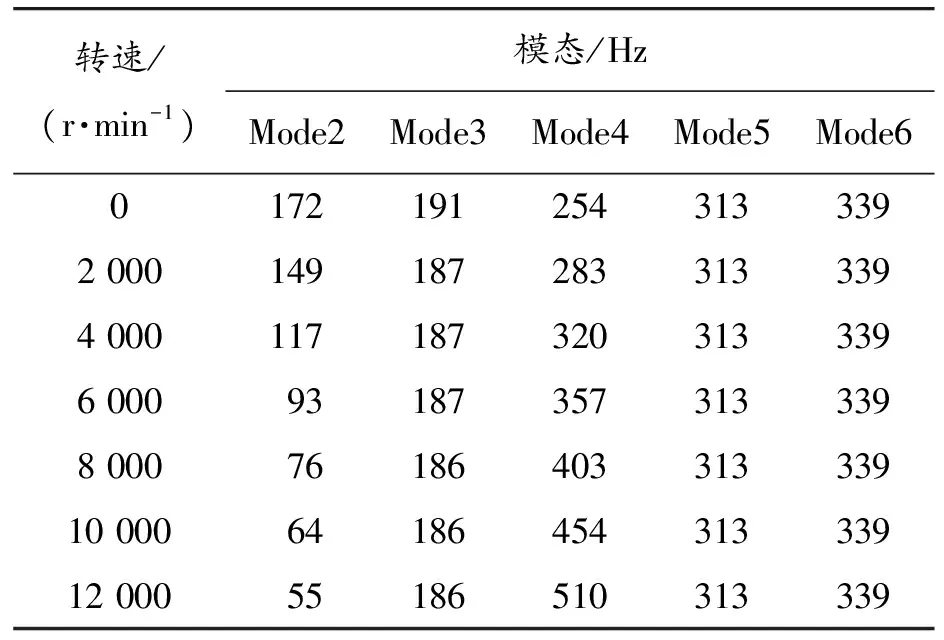
表4 框架-轴承-转子系统惯性转速与模态数据

考虑陀螺效应后:第二阶模态频率随惯性转速升高而降低,第四阶模态频率随惯性转速升高而增大,第三、五、六阶模态频率随惯性转速变化不明显。

将表4中数以惯性转速为横坐标,以模态频率为纵坐标绘制成图8所示的框架-轴承-转子耦合系统坎贝尔图。图中从原点引出一倍频激励直线,一倍频线与各阶模态曲线交点的横坐标值为系统所求的临界转速,纵坐标为该临界转速所对应的系统固有频率。

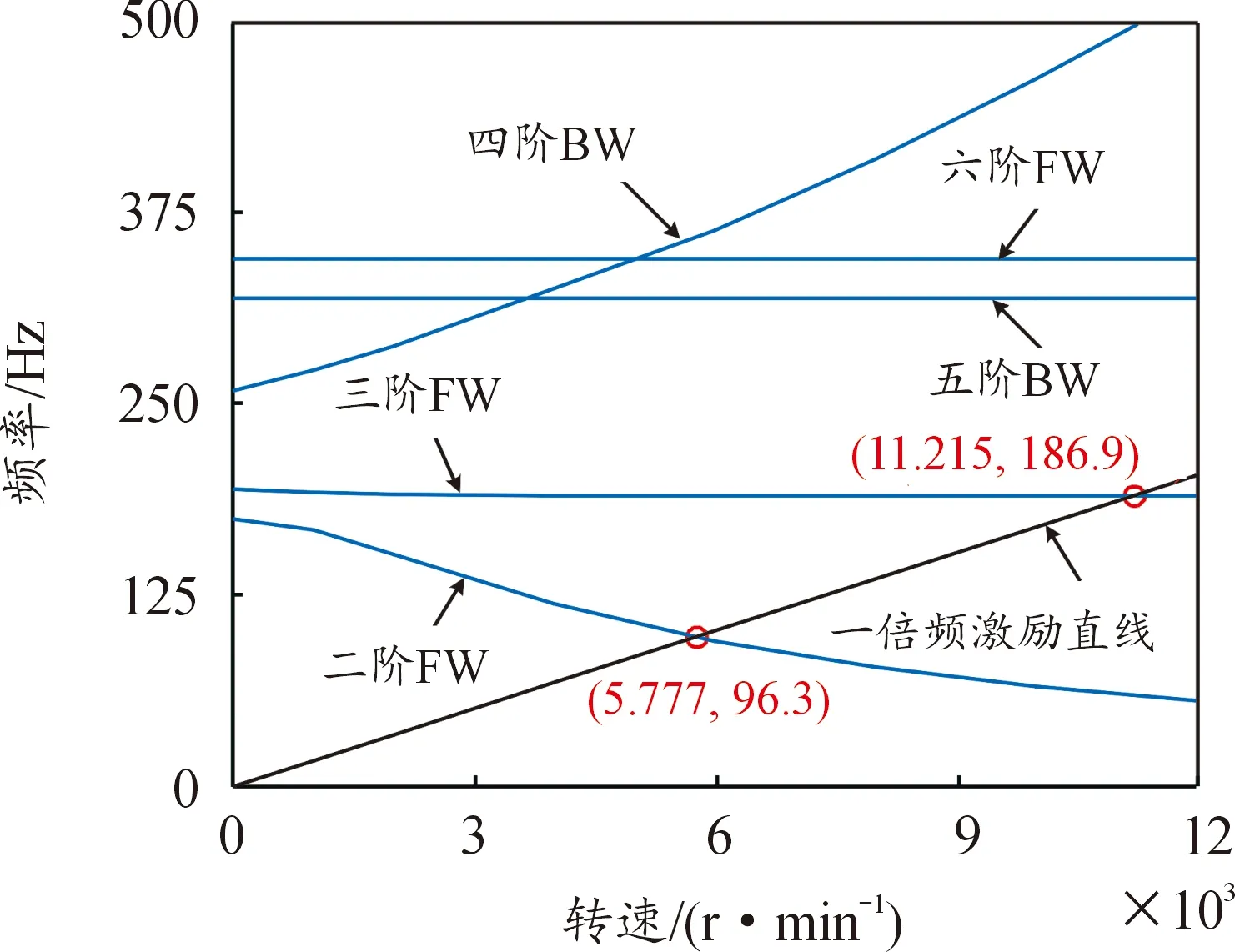
图8 框架-轴承-转子系统坎贝尔图

从图8可以看出,一倍频激励直线与二阶、三阶模态频率曲线的交点分别为系统对应的前两阶临界转速:一阶临界转速为5 777.4 r/min,二阶临界转速为11 215 r/min。

通过对比图5与图8发现,框架-转子系统与框架-轴承-转子系统的各阶模态频率随着惯性转速的变化趋势一致,临界转速对应的模态振型也一致,这从侧面反映出了分析结果与实际情况相符。但当考虑转子轴承径向刚度影响时,耦合系统整体模态频率有所下降,模态振型位移有所增大,系统一阶临界转速下降了4%左右,二阶临界转速下降6%左右。

将耦合系统的转子轴承径向等效弹簧刚度,从160～320 kN/mm以40等间距量递增变化。在不考虑轴承阻尼的影响,考虑了转子的陀螺效应。运用2.2节相同原理的坎贝尔图,得到5组不同轴承径向刚度下耦合系统的前两阶临界转速值,如表5所示。

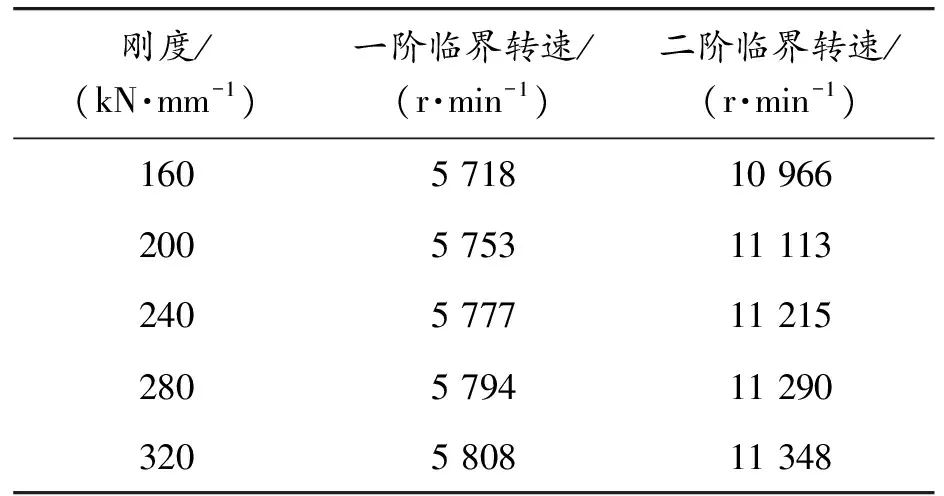
表5 转子轴承不同径向刚度与临界转速

将表5数据进行处理分析得出框架-轴承-转子耦合系统一、二阶临界转速随转子径向刚度变化的趋势线与敏感度曲线,如图9、图10所示。

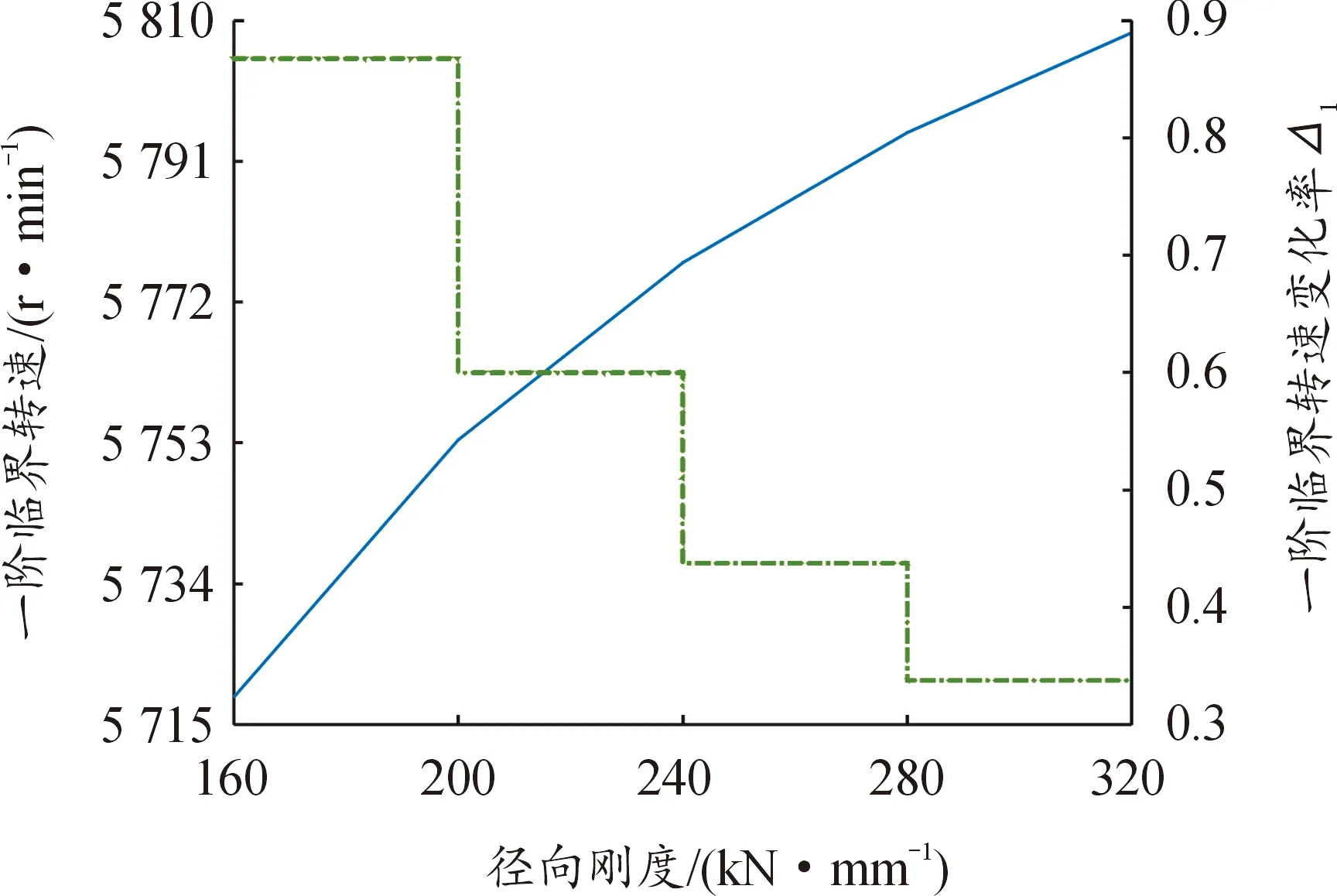
图9 一阶临界转速分析

从图9、图10可以得到,SGCMG框架-轴承-转子耦合系统的一、二阶临界转速都随着转子轴承径向刚度的增加而升高,但升高趋势变得逐渐缓慢,故当系统转子轴承径向刚度到达一定数值后,系统临界转速将趋于稳定。通过对比图9与图10中的临界转速变化率发现,二阶临界转速受径向刚度变化的影响大于一阶临界转速,且系统一阶临界转速对转子轴承径向支撑刚度的敏感度在1%以内,二阶临界转速对转子轴承径向支撑刚度的敏感度在4%以内。

3 耦合系统不平衡响应分析

控制力矩陀螺系统动力学特性影响最大的不平衡量源于转子部件的不平衡质量,转子的不平衡质量主要来源于转子的制造误差、材料不均匀、不对中、变形等诸多因素,但是转子的不平衡是无法避免的[15]。

根据式(1),F(t)是转子不平衡量引起的外载荷力向量。已知转子集中质量为m=26.72 kg,设偏心距为e=0.005 m,转子转速为Ω,则不平衡可以分解在转子平面的2个互相垂直方向上,为:

(6)

不平衡响应分析在ANSYS中对应谐响应分析模块,设置约束和前述完全一致,选取转子轴承径向刚度为240 kN/mm进行分析。由于在结构振动分析中,低阶频率是造成系统振动的主要频率成分,因此在谐响应分析时设置扫频范围为0～200 Hz。得到如图11所示的转子几何中心节点在转子平面X方向幅频响应,和图12所示的转子几何中心节点在转子平面Z方向的幅频响应。

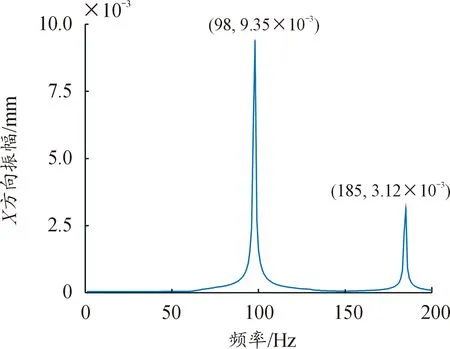
图11 转子中心节点幅频响应(X方向)

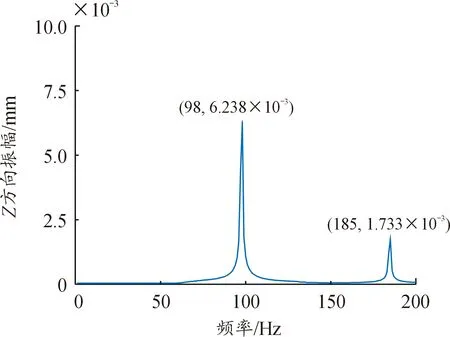
图12 转子中心节点幅频响应(Z方向)

从图11与图12可以得到,转子几何中心节点在转子平面X与Z方向都出现了2个峰值响应,且对应频率分别为98 Hz与185 Hz,在X与Z方向的响应相位角相差90°。其中98 Hz刚好与2.2节中,在240 kN/mm的轴承径向刚度所对应系统一阶临界转速频率(98.8 Hz)接近,185 Hz刚好与其二阶临界转速频率(186.9 Hz)接近,故证明了第2节中临界转速分析结果的正确性。一、二阶响应在X方向的幅值明显大于Z方向,反映出框架-轴承-转子耦合系统在X方向的振动更为剧烈。同时一阶响应幅值比二阶大,反映出耦合系统一阶临界转速附近的振动更加剧烈。

4 框架-轴承-转子耦合系统瞬态分析

要想了解系统在时域上的连续变化过程,需要进行时间历程分析(亦称瞬态动力学分析)来确定系统承受随时间变化载荷的结构动力学响应[16-18],求解方法有:完全法、缩减法、模态叠加法,本章采用完全法求解。以SGCMG框架-轴承-转子耦合系统为研究对象,其中等效轴承径向弹簧刚度设置为240 kN/mm。在耦合系统上框架电机安装位置处对转子施加如图13的转速载荷,始终将SGCMG框架两端固定。

图13 转速载荷曲线

经过有限元软件求解,得到了框架-轴承-转子耦合系统有限元求解结果。分别提取了上框架中心、转子中心、下框架中心(见图14)在转子平面X与Z方向,以及转子轴向Y的位移响应的时域与频域结果,如图15—20所示。

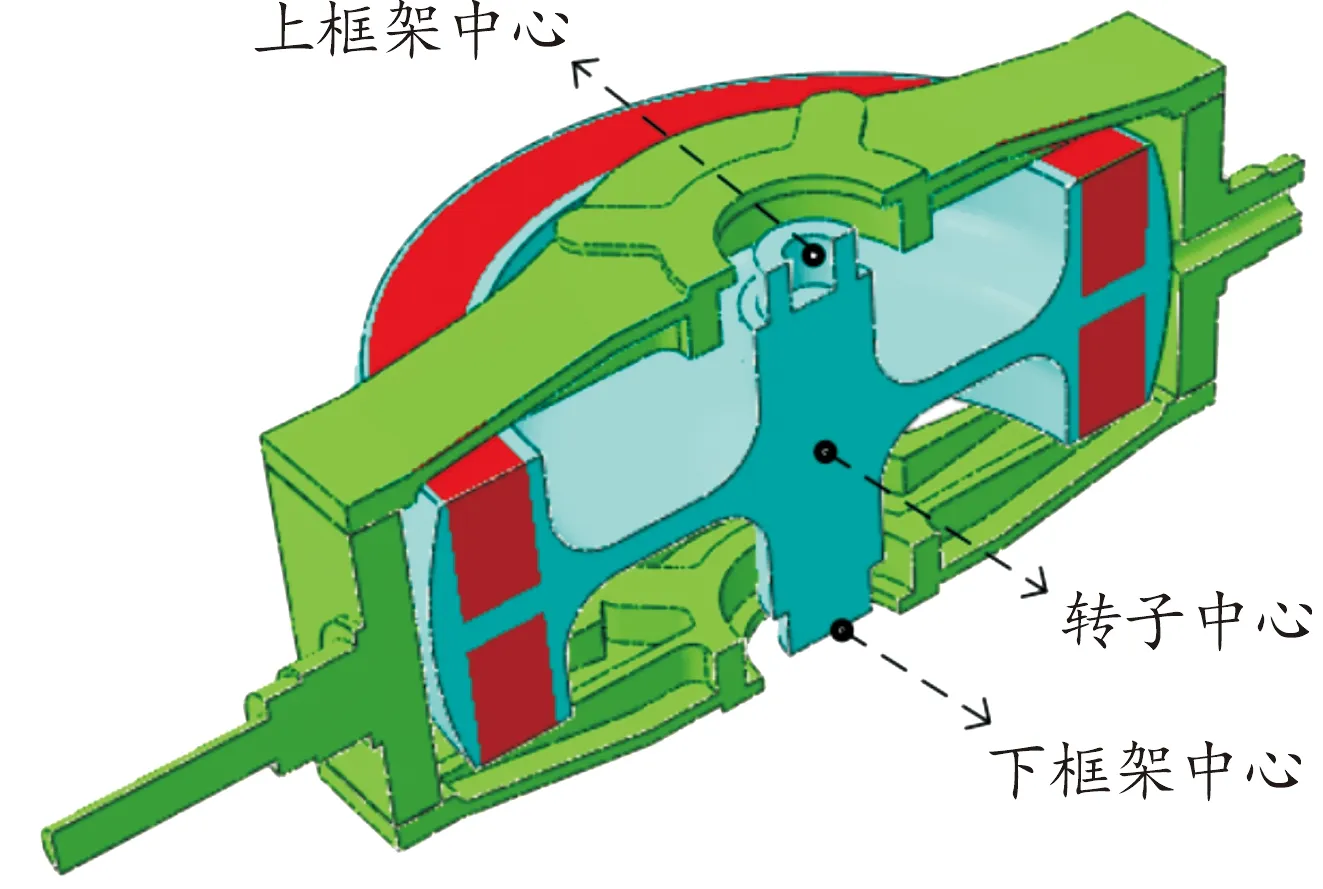
图14 CMG剖面图(沿X-Z)

图15 稳态位移响应时域图(X方向)

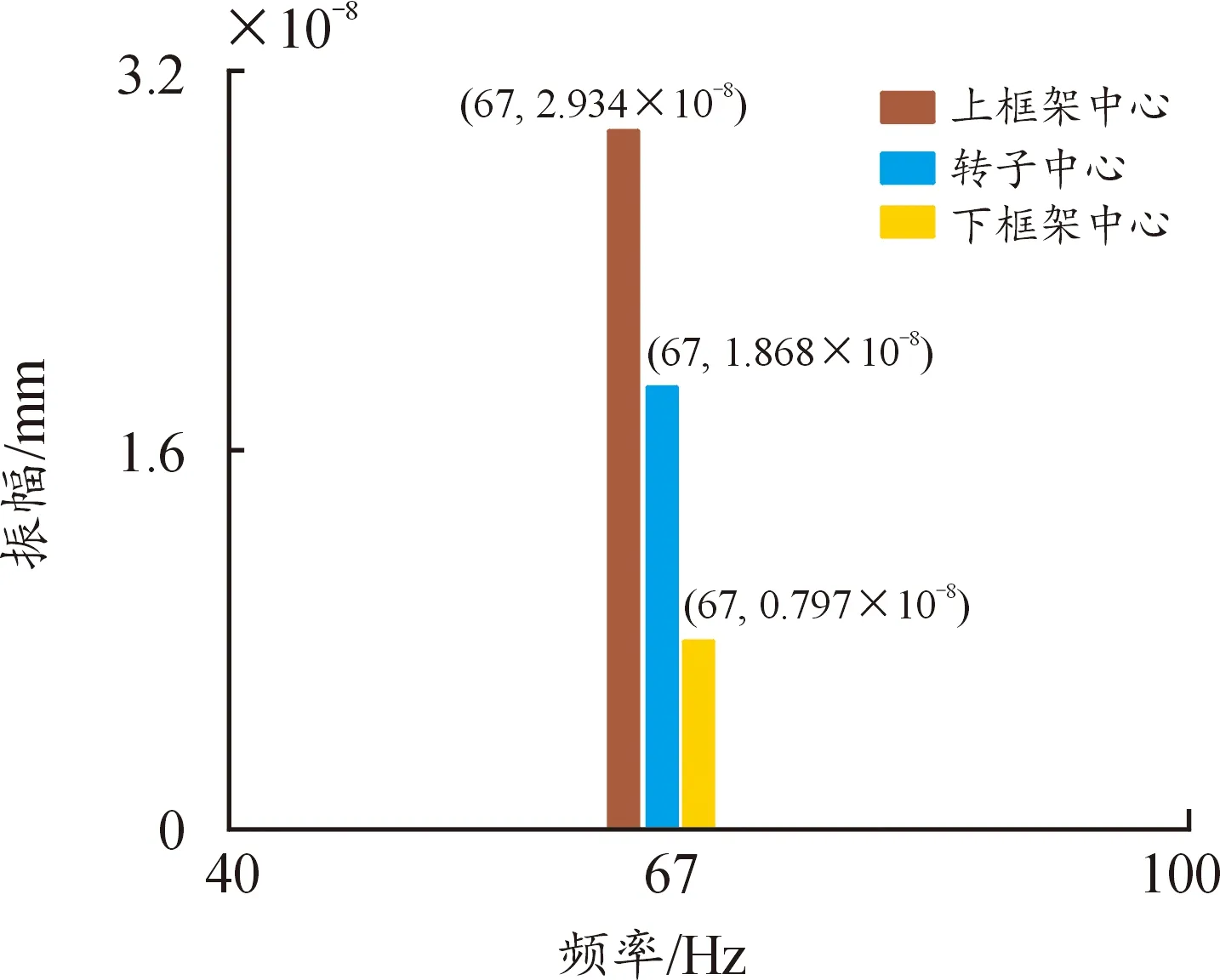
图16 稳态位移响应频域图(X方向)

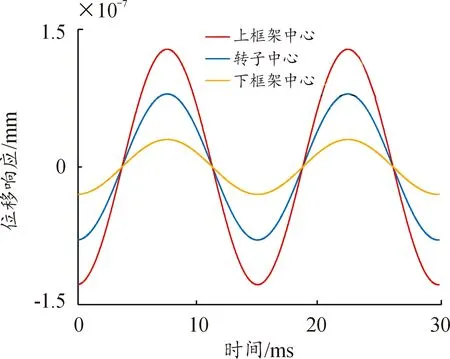
图17 稳态位移响应时域图(Z方向)

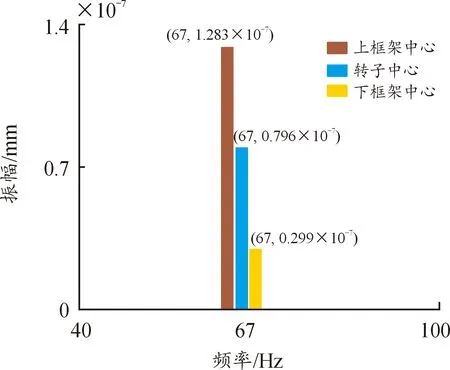
图18 稳态位移响应时域图(Z方向)

图19 稳态位移响应时域图(Y方向)

图20 稳态位移响应时域图(Y方向)

通过分析得出,框架-轴承-转子耦合系统在4 000 r/min稳态工况下的响应结果总结如下:

1) 上框架中心、转子中心、下框架中心在XZ平面内的位移响应以67 Hz同频振动,且X方向振幅分别为:2.934×10-8、1.868×10-8、0.797×10-8mm,Z方向振幅分别为:1.283×10-7、0.796×10-7、0.299×10-7mm。X方向与Z方向上框架中心的位移振幅大于转子中心位移振幅大于下框架中心位移振幅,依次接近线性增加。耦合系统在平面Z方向的振动比平面X方向的振动更为明显,幅值接近4.5倍关系。

2) 得到系统框架与转子在Y方向的位移几乎为同频同幅值的振动,振动频率为1 105 Hz与1 441 Hz,对应一阶振动幅值在1.93×10-6mm附近,二阶振动幅值在0.175×10-6mm附近。耦合系统在转子轴Y方向的振动显著大于转子XZ平面内的振动,接近100倍关系。

以上框架中心、转子中心、下框架中心在Z方向位移响应作为横坐标,X方向位移响应作为纵坐标,绘制如图21所示轴心轨迹图。

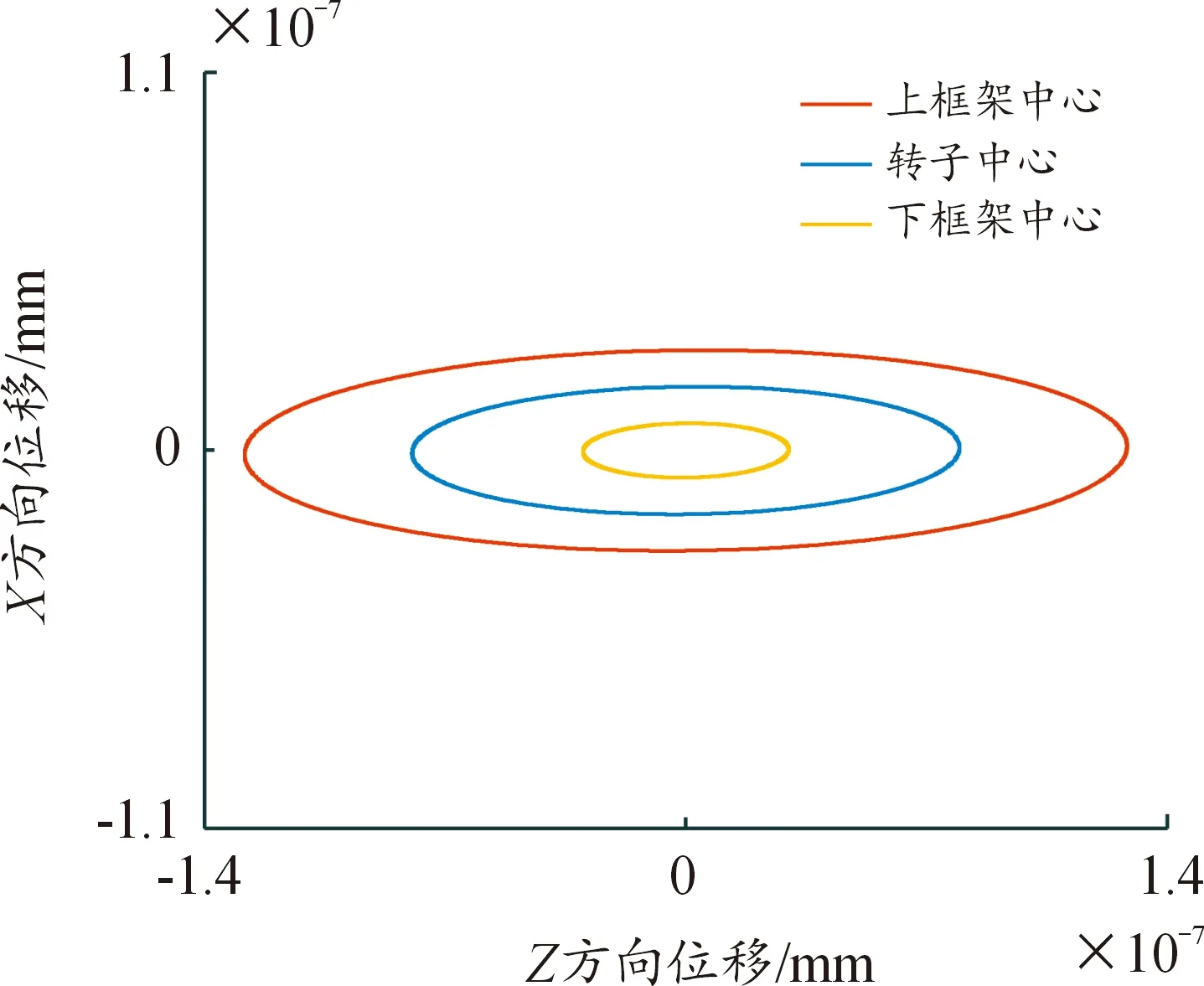
图21 稳态轴心轨迹(XZ平面)

从图21可以看出框架中心与转子中心在转子平面XZ内的运动轨迹为椭圆。且SGCMG上框架运动椭圆轨迹大于转子中心轨迹大于下框架中心轨迹,轨迹半径依次近似成2倍关系,由此可以判断转子动力驱动对耦合系统的振动贡献占比大。

5 结论

针对某两轮车载单框架控制力矩陀螺进行研究,通过Hypermesh与Ansys联合仿真的方式,建立了SGCMG框架-轴承-转子耦合有限元仿真模型。在此模型基础上,探究了耦合系统模态随惯性转速变化的规律及转子轴承径向刚度对系统临界转速的影响,研究了SGCMG转子在特定偏心质量下的系统不平衡响应,验证临界转速分析的准确性,最后,进一步研究了耦合系统在转子4 000 r/min稳态响应下振动特性。由仿真结果可以得出以下结论:

1) 本次设计的单框架控制力矩陀螺一阶临界转速为6 000 r/min左右、二阶临界转速为11 500 r/min左右,因此避免发生共振,转子稳态运动工况的最佳转速选择范围为0～5 000 r/min与7 200～9 200 r/min。

2) 当转子轴承径向刚度在大于160 kN/mm以上时,SGCMG系统临界转速对其变化敏感度不超过4%,表明转子轴承径向刚度对系统临界转速为非敏感因素。在后期工程应用中转子轴承选型时径向刚度控制在180～320 kN/mm范围内即可。

3) SGCGM转子在受到不平衡激励作用时,转子平面内X方向的振动比Z方向更为剧烈,因此在后期优化结构时,应该着重优化框架结构在X方向的强度。

4) SGCMG转子在稳态工况下,系统在转子轴Y方向的振动显著于转子平面XZ内的振动,且转子动力输入端框架的振动表现得最为明显。因此后续优化可采取非对称式框架结构来削弱振动。