深部软岩巷道围岩变形机理研究

焦若珂

（潞安化工集团有限公司 古城煤矿，山西 长治 046000）

0 引 言

随着我国经济的持续发展，煤炭资源的需求日渐增多，矿井深部开采已成为当前煤炭开采的主流[1-2]。在深部开采条件下，高温、高压带来的围岩剧变、蠕变等特征日益明显[3-4]，浅埋煤炭支护已经无法满足矿井的安全生产要求，因此需要对深埋条件下巷道围岩变形机理进行深入研究，制定有效的巷道围岩支护形式，实现深部围岩变形控制[5-6]。国内外众多学者对深部软岩巷道进行深入研究，取得重要的研究成果。张国宝[7]等人以常村矿3107 工作面回风巷为工程背景，通过对原支护参数、围岩变形失稳特征及采动因素分析，提取剥除浅层破碎围岩后锚网索补强支护等方案，从而实现巷道围岩的变形控制；高凤伟[8]等人基于深部开采高应力，复合顶板、大断面、采动影响等特点提出全断面高预紧力锚索支护技术，并通过数值模拟和现场工业性实验等方法，研究确定技术方案等对围岩变形控制的有效性，减少了巷道的二次返修频率；王文才[9]等人基于耦合支护理论，提出“锚杆（索）+锚网+注浆”等的支护方案，实现工作面顶底板和两帮的有效控制。上述研究丰富了深部围岩控制的内容，但是多注重技术应用的研究，对深部矿井变形的内在机理研究较少，本文以古城煤矿北二2 号回风大巷为研究背景，通过围岩变形机理研究，确定巷道变形影响因素，为矿井变形控制提供依据。

1 概 况

北二2 号回风大巷布置在3 号煤层中，3 号煤层位于山西组下部，属稳定型煤层，煤层厚3.35～9.65 m，平均6.05 m，含0.2 m 厚泥岩、炭质泥岩夹矸，煤层平均倾角为0～18°，埋深平均655 m。巷道顶底板岩性如图1 所示。

2 弹塑性区理论解析

基于弹塑性力学理论，假设半径为Ro 的圆形巷道，在埋深H≥20 Ro 条件下，巷道处于理想受力状态，将模型简化为平面应变问题，忽略巷道围岩蠕变因素，巷道围岩变形破坏符合摩尔库伦模型。依据模型，巷道围岩由浅入深可分别划分为破碎围岩区、塑性围岩区、弹性围岩区和原岩应力围岩区，具体如图2 所示。基于图示力学模型分别进行弹性围岩区和塑性围岩区的力学及位移数值解析。

图2 巷道围岩力学模型Fig.2 Mechanical model of roadway surrounding rock

2.1 基本方程

极限平衡区静力平衡方程：

极限平衡条件为：

式中：σt、σr分别为切向应力与径向应力，MPa：φ为岩体内摩擦角，（°）；C为岩体内聚力，MPa；R 为极限平衡区内所研究点的半径，m。

将式（2）代入式（1）中，变形整理得到弹性区与塑性区方程。

2.2 弹性区应力方程

径向应力为：

式中：pO为原岩应力，MPa；pi为支护阻力，MPa：RO为巷道半径，m；C 为岩体内聚力，MPa；φ为岩体内摩擦角，（°）。

2.3 塑性区应力方程

径向应力为：

切向应力为：

塑性区半径为：

周边位移为：

式中：G 为剪切弹性模量，GPa。

在采动应力影响下，巷道围岩变形加剧，由于采动应力无法直接量化，但可通过围岩所受集中应力情况间接反映采动应力变化情况，因此通过施加应力增量，即在原岩应力基础上增加（1+K）po，则巷道围岩在采动条件下的Rs和u 分别为：

基于矿压理论并结合式（4）和式（5）分析，巷道围岩弹性状态下受力可由R表示，同时围岩塑性破坏后，破碎围岩体内产生的应力变化可由表示。需要注意的是，弹性区范围内的围岩变形受到塑性区范围内破碎岩的抑制，若清理破碎围岩，则巷道尺寸增加，同时释放弹性区围岩变形，增加塑性区的破坏范围，不利于巷道围岩的变形控制。

分析式（9）可知，塑性区半径RS、位移u受到地应力po、支护阻力pi、岩体内摩擦角φ与内聚力C等因素的影响，因此为了进一步研究各个因素的影响程度，故接下来进行不同因素下对巷道塑性区发育状况的影响研究。

3 不同因素对巷道影响研究

从定量角度出发分析地应力p0、岩体内摩擦角φ、内聚力C与塑性区半径、周边位移的关系。当巷道未采取支护措施时，认为pi=0；当巷道采取支护措施时，认为pi≠0，同时针对每个因素进行数值模拟验证。

3.1 不同埋深对巷道变形影响

巷道围岩地应力p。通过其岩体的垂直应力体现，而岩体的垂直应力与巷道埋深有直接的关系，通过改变煤层埋藏深度分析地应力对巷道变形程度的影响。北二2 号回风大巷部分范围处于不稳定围岩环境，其巷道围岩主要为泥岩和煤，因此分析不稳定围岩对确定巷道影响因素十分必要。分析处于100～800 m 埋深条件下的回采巷道塑性区半径及其周边位移，为方便计算取pi=0。

在200、400、600、800、1 000 m 等不同埋深条件下进行巷道塑性区模拟，如图3 所示。

图3 不同埋深巷道塑性区分布Fig.3 Distribution of plastic zone in roadway with different buried depth

分析图3 可知，在埋深200～600 m 时，塑性区变化明显，当埋深大于600 m 后，塑性区变化范围基本相同，但在局部范围塑性区有所扩大，同时随着埋深的增加，巷道当前正在破坏区域逐渐增加，当埋深处于200 m 时，巷道围岩过去发生破坏而当前未继续发生破坏，为图中浅色区域，当埋深增加至400 m 时，深色区域逐渐增加，尤其是巷道中部和两底角位置，说明当前巷道围岩不仅过去发生过破坏，当前仍在继续破坏，当埋深大于600 m时，巷道围岩基本被深色区域覆盖，说明当前巷道围岩极不稳定，而且塑性区有进一步纵深扩展的可能，需要注意的是，在埋深超过800 m 后，巷道浅部围岩已完全发生破坏，其中顶板和两底角区域纵深范围较高，两帮区域较小。

3.2 不同内摩擦角对巷道变形影响

分析岩体的强度参数内摩擦角φ影响巷道围岩的变形程度，并分析其对巷道塑性区半径及周边位移的影响，取pi=0。

软岩岩体中，内摩擦角变化较小，设置内摩擦角变化范围为30°～35°，其他地质参数与上述相同，内聚力取2.0 MPa。本文分别模拟了30°、31°、32°、33°、34°和35°内摩擦角塑性区分布图，具体如图4 所示。

图4 不同内摩擦角下巷道塑性区分布图Fig.4 Distribution of plastic zone in roadway under different internal friction angles

分析图4 可知，随着内摩擦角的逐渐增大，巷道围岩塑性区范围逐渐减小，当内摩擦角由30°增加至32°时，巷道浅部围岩区域变化不大，但顶板深部围岩塑性区范围逐渐减小，当内摩擦角继续增加至33°时，巷道围岩塑性区范围明显减小，其中尤其是浅色表示区域，即过去发生破坏，当前仍继续发生破坏减小明显，深色区域，即过去发生破化，当前不再发生破坏，有所增加，当内摩擦角增加至34°时，巷道围岩范围持续减小，同时浅色区域基本消失，当内摩擦角继续增加至35°时，巷道浅部围岩完整性进一步提高，顶板和两帮区域破坏范围较小，但是在底角区域破坏仍较为明显。

3.3 不同粘聚力对巷道变形影响

分析岩体的强度参数内聚力C共同影响巷道围岩的变形程度，分析其对巷道塑性区半径及周边位移的影响，取pi=0。

软岩内聚力一般在0～ 5 MPa，基于前述地质参数，取北二2 号回风大巷平均埋深为655 m，巷道半径4.2 m，岩体容重25 kN/m3，泊松比为0.25，剪切模量为2.35 GPa；内摩擦角为35.14°，本文分别模拟了1、2、3、4、5 MPa 粘聚力塑性区分布图，具体如图5 所示。

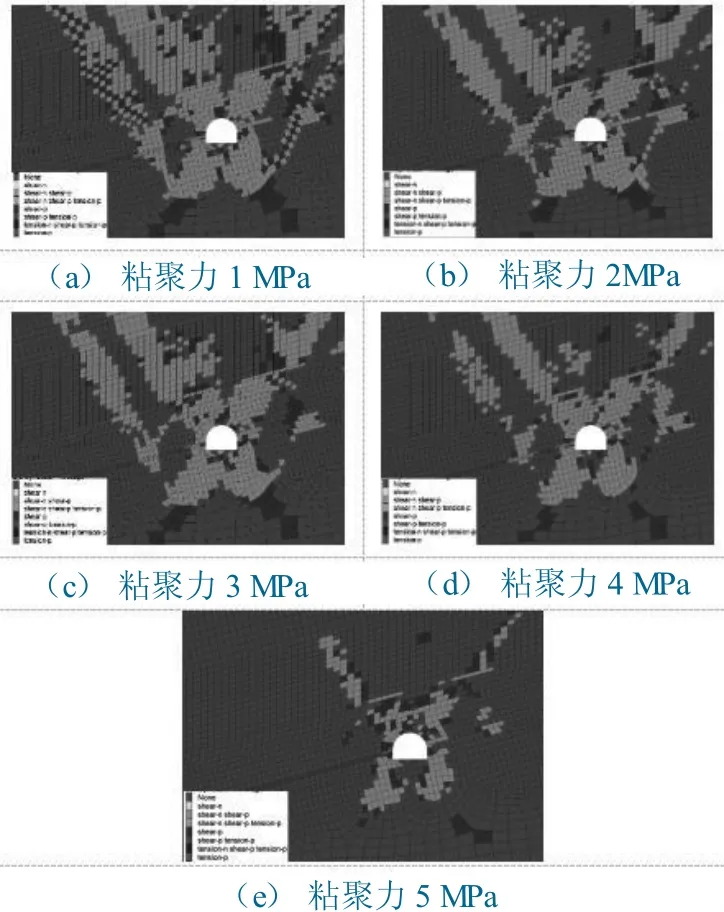
图5 不同粘聚力下巷道塑性区分布图Fig.5 Dstribution of plastic zone in roadway under different cohesion

分析图5 可知，粘聚力对巷道塑性区发育有一定限制作用，但限制效果不明显，当粘聚力由1 MPa 增加至4 MPa 时，巷道围岩塑性区范围减小不明显，当粘聚力继续增加至5 MPa 时，塑性区范围降低，同时深色区域，过去发生破坏，当前未继续发生破坏的区域逐渐增加，塑性区未破坏区域扩大，因此，若需要对围岩塑性区发育进行限制，需要保持粘聚力在较高水平。

综上所述，基于不同埋深、粘聚力和内摩擦角等不同因素对软岩巷道影响性分析，确定在埋深一定情况下，增加围岩粘聚力、内摩擦角度，对巷道塑性区变形都具有一定的控制作用，其中巷道粘聚力以2.5 MPa 为拐点，内摩擦角以33°为拐点，继续增加后对塑性区控制效果降低。

4 结 论

本文通过理论分析、数值模拟等方法进行深部软岩巷道围岩变形机理研究，获得如下结论。

（1）基于弹塑性力学理论建立围岩弹性区力学模型，确定塑性区半径和位移受地应力、支护阻力、围岩内摩擦角和内聚力等影响。

（2）通过数值模拟确定在埋深确定情况下，粘聚力在2.5 MPa 范围内和内摩擦角在33°范围内对巷道塑性区变形有一定控制作用，继续增加后对塑性区控制效果降低。