基于参数协同自适应的VSG 控制策略研究

张晓辉，党 媛，党存禄

（1.兰州理工大学 电气工程与信息工程学院，兰州 730050；2.兰州工业学院 电气工程学院，兰州 730050）

近年来，以风光为代表的可再生能源的渗透率不断升高，微网的概念得到国内外广大学者的研究[1]。传统的并网逆变器具有柔和可控性，惯量低、欠阻尼、响应速度快，难以为微源接入电力系统提供必要的惯量和阻尼支撑。大规模接入的新能源和电力电子器件，在受到干扰后，会使低惯量电力系统的频率调节能力减弱[2]。为了解决电力电子器件惯性和阻尼不足的问题，学者们借鉴传统发电机的运行模式，即通过控制算法模拟同步电机的外部特性，有效提高新能源高渗透系统的惯性和阻尼水平。基于该思想，虚拟同步发电机技术（VSG）应用而生[3]，在暂态过程中，通过VSG 的惯量和阻尼来减小系统的频率波动，并补偿功率差额，以抑制系统的振荡来增强系统的稳定性[4]。惯性常数和阻尼系数是传统发电机固有的特性，惯量和阻尼是改善系统动态性能的关键[5]。VSG 可以通过自适应控制调节虚拟惯性和阻尼来改善其动态特性。当电源侧有功出力发生变化或负荷出现扰动时，可能会出现暂态振荡。针对VSG 分布式电源并网时出现的功频振荡问题，文献[6]通过分析暂态过程中功率和频率的变化机理，提出参数自适应控制算法，改善了功频响应特性。上述文献只考虑了转动惯量对功频稳定性的影响，并没有考虑阻尼的作用；文献[7]通过分析同步机惯量和阻尼与系统频率的关系，提出一种惯量阻尼自适应综合控制算法，实现VSG 参数的交错控制。

基于以上分析，本文提出一种基于参数协同自适应的VSG 控制策略，使VSG 虚拟参数能更好地跟踪频率波动，并设置频率偏差和频率变化率阈值进行自适应，避免了由于频率波动小而引起的虚拟惯量和虚拟阻尼的频繁变化，减少了自适应算法的计算量。最后，通过仿真验证了本方案的有效性。

1 VSG 控制基本原理

1.1 VSG 数学模型

VSG 控制结构如图1 所示。采用VSG 控制的并网逆变器的基本工作原理是：电网调度层根据调度信息给出有功功率指令Pref和无功功率指令Qref。同时，通过在线监测装置测量逆变器电网侧的有功输出Pe和无功输出Q。根据上述功率参数，通过VSG控制算法得到VSG 输出电压与电网电压的相位差，即功角δ 和输出电压E，然后通过电压电流双环控制得到输出信号，作用于开关管的通断。控制系统为三环控制，外环是由虚拟励磁器和虚拟调速器组成功率控制环，用以提供系统的频率和电压支撑；内环为双环控制，在加快电流的跟随性的同时，维持VSG 输出电压。

图1 VSG 控制原理图Fig.1 VSG control schematic diagram

极对数为1 的VSG 转子运动方程为

式中：Pm为机械功率；Pe为电磁功率；J 为虚拟惯量；D 为虚拟阻尼系数；ω 为实际角速度；ω0为额定角频率；δ 为VSG 的功角。

根据同步发电机的一次调频，VSG 的功频控制方程为

式中：Pref为给定有功功率；Km为有功下垂系数。

同理，VSG 的无功-电压控制由励磁控制器来实现，通过调节虚拟电势E 以维持VSG 输出电压的稳定。励磁调节控制方程为

式中：E、E0分别为励磁电动势和空载电势；Uref、U 分别为VSG 输出电压的参考值和实际值；KQ是无功调节系数；KV是电压调节系数。

由式（1）和式（3）可得VSG 的控制框图如图2所示。

图2 VSG 控制框图Fig.2 Control block diagram of VSG

VSG 的三相给定电压为

式中：Ep为相电压的幅值；φ 为VSG 的相位。

1.2 参数J 和D 对VSG 输出特性的影响

1.2.1 J 和D 对有功功率输出特性的影响

VSG 的输出功率如式（5）所示：

式中：U 为机端电压；θ、Z 分别为线路阻抗角和阻抗。Z 和θ 的表达式为

式中：R、L 分别为电阻和滤波电感。当线路阻抗为感性时，L 远大于R，取R=0，可得：

由式（1）和式（7）可得，VSG 有功功率传递函数如式（8）所示：

则自然振荡角频率ωn和阻尼比ξ 分别为

若ξ 的取值范围为0～1，误差带为±5%，则系统的超调量σ%和调节时间ts为

在功率指令给定的情况下，根据式（8）可得，VSG 的有功功率输出响应曲线，如图3 所示。

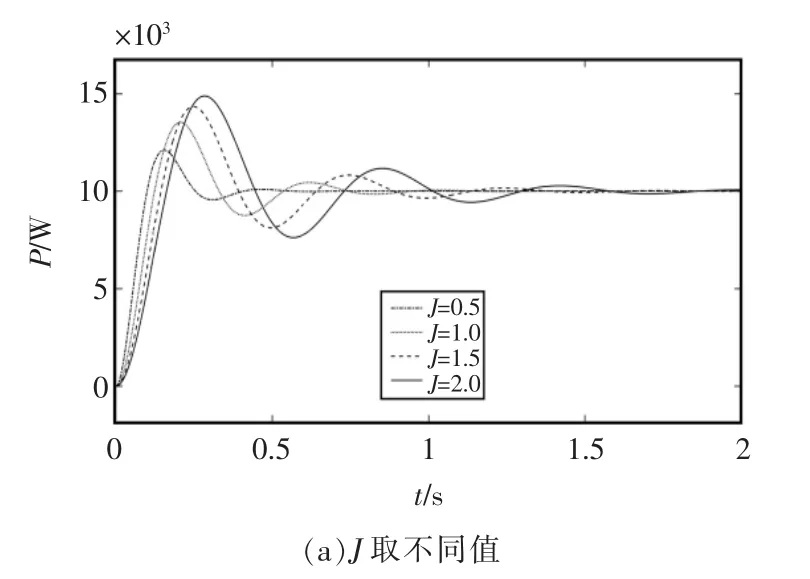
图3 有功功率阶跃响应曲线Fig.3 Step response curve of active power

由图3 可以看出，当J 增大时，VSG 的有功超调量也增大，功率出现振荡现象，这是由于自然振荡角频率ωn的逐渐减小，因此振荡变得愈剧烈，且稳定的时间变长；随着阻尼系数D 的增大，系统阻尼增加，有功功率的超调量逐渐减小且上升时间增大，这是由于阻尼比ξ 逐渐增大，响应曲线越平稳，系统更加稳定。

1.2.2 J 和D 对角频率输出特性的影响

在功率指令给定，即有功功率为10 kW，无功功率为0 的情况下，角频率变化的评价指标如图4 所示。由图4（a）可以看出，同时增大J 和D 会导致暂态过程中角频率的过冲量Δωmax减小，反之，则会使其增大；由图4（b）可得，当J 增大时，调节时间ts也随之增大，在D 增大的过程中，ts先减小后增大，这是由于在暂态过程中，阻尼较小时，不能快速抑制过大的振荡。但随着D 的增大，系统的响应速度逐渐变慢，调节时间变长。

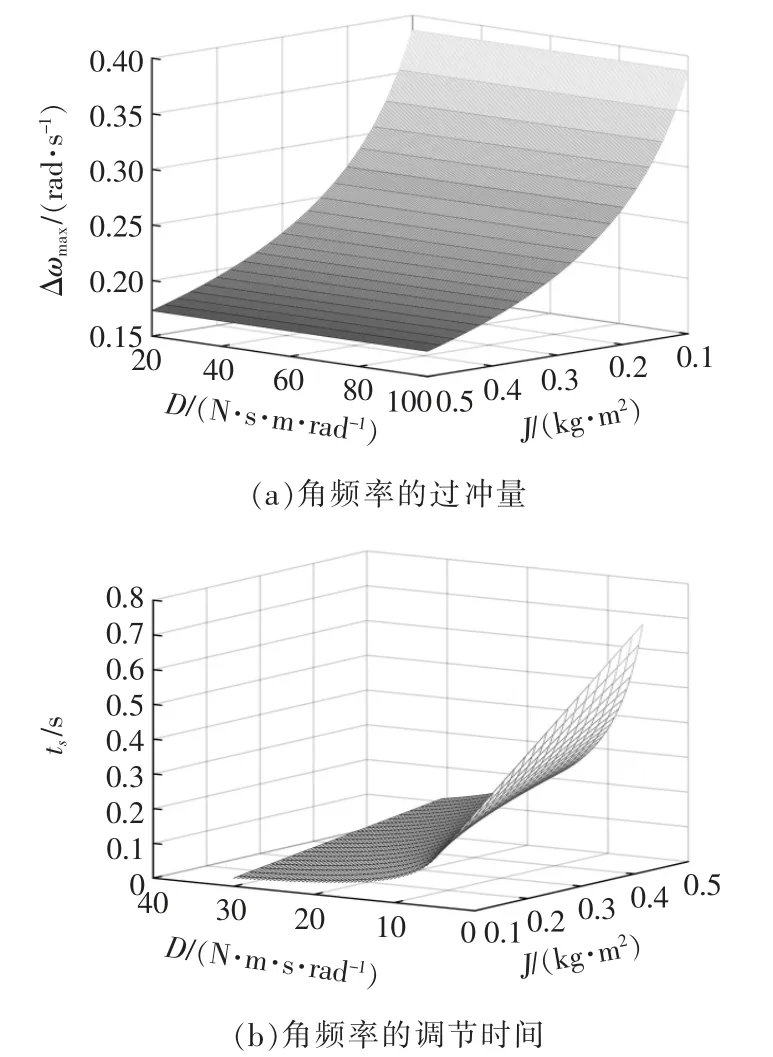
图4 不同J 和D 对角频率输出特性的评价指标Fig.4 Evaluation indexes of angular frequency output characteristics of different J and D

综上，VSG 的动态性能由J 和D 共同决定，对输出特性相互制约。减小J 虽然实现了功率的快速响应，但会使角频率变化率增大；增大J，频率波动减小，但会带来系统振荡。另外，当D 较大时，可抑制功频振荡，但会减缓系统响应的快速性。因此，应折中考虑性能指标，选取合适的J 和D。

2 VSG 参数自适应算法

2.1 J 和D 整定原则

同步发电机的功角和角频率振荡曲线，如图5所示。

图5 同步发电机功角、角频率振荡曲线Fig.5 Power angle and angular frequency curves of synchronous generator

当系统受到扰动时，系统发生振荡。根据角频率振荡曲线，一个振荡周期［t1，t5］可分为4 个阶段，当系统处于振荡周期的第1 阶段（t1～t2）时，P2>P1，ω>ω0，dω/dt>0，dω/dt 先增加后减小，因此，需要增大J 和D 来抑制dω/dt 的突变，同时减小频率偏差；当系统处于第2 阶段（t2～t3）时，P3>P2，ω>ω0，dω/dt<0，dω/dt 由缓慢减小到迅速减小，此时需要减小J 以加速ω 的回调，使其快速趋向于ω0。同时应增大D，进一步抑制角频率的偏移；在阶段3（t3～t4）和4（t4～t5），J 和D 的选取原则与阶段1 和阶段2 类似。

综上，可根据角频率变化率及其偏差来确定J和D 的选取原则，如表1 所示。

表1 不同阶段J 和D 的变化情况Tab.1 Changes in J and D at different stages

2.2 参数自适应控制策略

由上述分析可知，虚拟惯性J 由频率变化率dω/dt 和频率偏差Δω 共同决定，虚拟阻尼D 主要由频率偏差决定，但若同时考虑频率变化率，则该D参数可更快地跟踪系统频率变化。同时，为避免J、D参数在频率小波动下频繁变化，提高VSG 的动态性能，自适应控制阈值仅设置dω/dt、Δω 满足阈值条件时，J、D 参数将发生变化。在J 发生变化时，为了避免尖刺现象的产生，可引入惯性环节，使系统更加稳定地过渡到下一阶段。据此，设计一种自适应控制策略如下：

式中：J0和D0分别为VSG 稳定运行时的J/D 值；Kj和Kd分别为惯量和阻尼的调整系数；Tj和Td分别为dω/dt 和Δω 变化阈值；T 为惯性时间常数。

2.3 参数整定

根据文献[6]对参数J 的整定，J 需要满足以下条件：

根据式（1），当系统处于稳态时，角速度不变，阻尼系数D 须满足：

3 仿真分析

为验证所提控制策略的合理性，利用Matlab/Simulink 平台进行仿真验证，仿真系统主要参数如表2 所示。

表2 仿真系统主要参数Tab.2 Main parameters of simulation system

采用单机VSG 运行在并网模式下，仿真时长为2 s。在初始阶段不带负荷运行，在0.5 s 时有功参考值从0 突增到15 kW，1.2 s 时又恢复到初始状态，无功功率恒定。

在不同的控制策略下，VSG 的有功功率输出和频率响应曲线，如图6 和图7 所示。

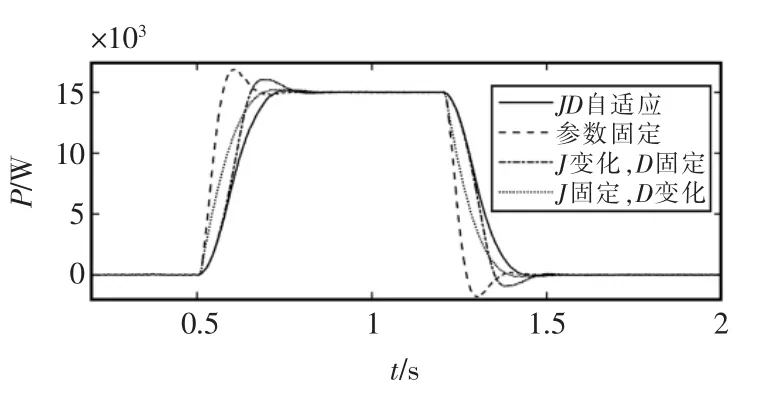
图6 不同控制策略下的有功功率对比Fig.6 Comparison of active power under different control strategies

图7 不同控制策略下的频率对比Fig.7 Comparison of frequency under different control strategies

由图6 和图7 可以看出，当系统增加有功输出时，VSG 转动惯量J 和阻尼系数D 采用参数固定时有功功率和频率响应曲线均具有较大超调，调节时间也相应较长，系统受振荡的影响比较严重；当J 单独变化时，有功功率的振荡频率发生变化；当D 单独变化时，振荡的衰减速率发生变化；J/D 自适应控制时的有功超调量和调节时间、频率偏差相对较小，控制效果得到进一步提高。

参数协同自适应控制时J 和D 的变化情况，如图8 所示。

图8 J/D 自适应控制的参数变化Fig.8 Parameter change of J/D adaptive control

由图8 可以看出，在0.5 s 突增负荷的情况下，VSG 的参数J 和D 均发生连续变化。在起始阶段，J和D 均增大，以抑制暂态过程中的功频振荡现象；在有功功率响应和频率恢复过程中，虚拟惯量和虚拟阻尼的值都恢复到初始参数，这是由于振荡时的频率变化率和频率偏差值都为0 造成的。

综上所述，本文提出的改进VSG 控制策略具有更好的动态性能。自适应J 和D 参数的改变不仅可以减小最大频率偏差，还可以降低有功功率超调量，缩短调节时间，说明了VSG 的灵活性和可控性。

4 结语

针对传统可再生能源接入电网时可能出现的功率振荡和频率波动问题，本文提出了一种基于参数协同自适应的VSG 控制策略，通过仿真对比分析得到以下结论：通过建立VSG 的数学模型，分析暂态过程中参数变化对功频特性的影响，虚拟惯量主要影响振荡频率，阻尼系数主要影响振荡的衰减速率；所提控制策略同时兼顾响应的快速性与系统的稳定性，有效抑制暂态过程功频振荡，改善有功输出与频率的响应特性，控制效果得以有效提升。