离散几何在建筑计算性设计中的应用：一个框架性描述

王晖

叶子超

刘梦嫚

丁一

秦阗怡

一、引论

几何学是对建筑学构成支撑的基础学科之一。从古埃及到中世纪再到近现代时期，从建筑的意匠构思到设计法则乃至施工建造，几何原理都持续扮演着重要的角色。建筑领域对几何学的应用研究由来已久，少数建筑师如G.笛沙格（Girard Desargues）和B.富勒（Buckminster Fuller）等人，也对几何学作出过突出的贡献。近年来奥地利计算几何学家H.波特曼（Helmut Pottmann）明确提出了建筑几何学（Architectural Geometry）的概念[1]，它可以理解为面向建筑领域的几何学相关知识的集成。与过去相比，当代建筑设计在复杂性、系统性和设计建造一体化等方面有更高的要求，因此对几何学原理的需求也更为迫切。

目前建筑几何学中讨论较多的是拓扑几何、分形几何、微分几何和计算几何等，已有丰富的研究成果。与这些几何门类相比，本文所探讨的离散几何（Discrete Geometry）不太为人们所熟知。离散几何也称为组合几何①（Combinatorial Geometry），是研究“离散”几何对象如点、直线、圆、多边形、多面体、球体、多胞体（高维空间）等的组合性质和排布规律的几何分支[2]。其中“离散”的基本意义是指元素的相对独立、分离状态，与“连续、不可分”的意义相对立。形态组合对设计工作的重要性不言而喻，尤其建筑设计而言，很多环节的工作从抽象层面都可以看作二维或三维形态的组织问题。因此，离散几何必然与建筑设计之间有密切的关联性。

随着智能化工具的普及，计算性设计成为当代建筑设计的前沿研究领域之一。按照孙澄教授的定义，建筑计算性设计是基于人居环境系统科学与复杂性科学思想，面向建筑方案创作需求，应用适宜的人工智能技术，展开多性能目标耦合考虑下的建筑设计元素自组织生成与自适应优化，生成建筑设计方案的过程[3]。建筑计算性设计的研究范畴可以更为宽泛，例如有学者认为也包含信息感知与知识表示、模型与学习方法、多维评价方法等方面[4]。

建筑计算性设计依赖人工智能技术的支撑，后者可分为数据驱动和规则驱动两种大的类型[5]。近两年以数据驱动为特征的AI 技术发展迅速，引发了全社会的关注，但在建筑计算性设计等专业细分领域，规则驱动仍然占有极为重要的位置。与过程不可解析、不可控制的“黑箱”智能相比，规则驱动的优势包括内在逻辑性强、过程相对可控、计算速度快、逻辑演绎方法具有更好的创新探索能力等。

离散几何的研究对象具有直观性和可计算性强的特点，它们的组合性质和排布规律，对基于规则驱动的计算性设计有重要支撑作用，特别是在数理规则引导下的形态生成、模式穷举、性能评价与优选等方面。然而迄今为止在建筑设计领域对于离散几何还缺乏清晰的讨论，不少案例已涉及了离散几何，但未能明确基础原理及其在几何学体系中的定位。因此，本文主要面向建筑计算性设计的应用需求，梳理离散几何的相关概念，探讨一般性的应用范畴和应用潜力，初步构建认知框架和应用体系，以充实当代建筑几何学的理论内涵。

二、离散几何相关研究范畴

离散几何主要在20 世纪获得了显著发展，数学家László Fejes Tóth、H.S.M.Coxeter和Paul Erdös 等人奠定了现代离散几何的理论基础。自20 世纪80 年代以来，离散几何各分支在计算机工具的支撑下呈加速发展态势，应用范围已拓展到自然地理学、材料学、晶体学、分子生物学、计算机图形学、设计学等多个领域。在由欧洲数学学会和美国数学学会共同发布的新版数学学科分类目录（MSC2020）中，“凸体与离散几何”与其他90 多个分支如数论、拓扑学、分形几何等共同列入一级目录。

目前国内在离散几何方面的基础研究还相对薄弱，同时离散几何的知识体系相当庞杂，即使在数学界内部的看法也不完全统一，给应用研究造成了一定的困难。鉴于这种情况，本文首先基于国内外主流文献[6～10]进行了基础认知的梳理，尝试归纳离散几何范畴下与建筑计算性设计关系密切的分支。其中包含两大方面：作为内涵的基本范畴（直观研究对象）和作为外延的拓展范畴（学科交叉领域）。

1.离散几何的直观研究对象

基于维度的视角，可以把离散几何的直观研究对象分为两类：同维度几何对象的组合，以镶嵌（Tiling）为主；不同维度几何对象（主要涉及点与线）的组合，即关联问题（Incidence）。

1）同维度组合问题，此方面主要包括镶嵌、填装、覆盖以及格与离散群等。镶嵌是指用几何形体铺满空间，形体之间不存在空隙与重叠，研究较多的是二维平面镶嵌（Tessellation）和三维立体镶嵌（Honeycomb）。与镶嵌相关的概念是填装（允许空隙）和覆盖（允许重叠），如果将空隙或重叠部分看作图元，也可以将二者转换为镶嵌模式（图1）。

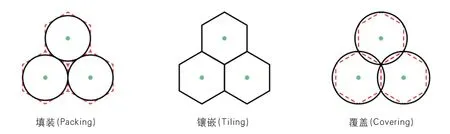
图1： 填装、镶嵌与覆盖

设计领域的既往研究多以对称性为依据，将镶嵌分为周期性（Periodic）、准周期（Quasi-periodic）与非周期（Aperiodic/Non-periodic）三种类型，但在离散几何体系下有更为精确的分类方式。在二维和三维范畴下，根据镶嵌元素的交边、交点性质，可将镶嵌分为从一般到特殊的四个层级[11]（图2）。一级为各类多边形和多面体构成的镶嵌，包括交边对交边镶嵌和非交边对交边镶嵌；二级分类在交边对交边镶嵌的基础上，对交点类型加以约束，如果镶嵌存在m 种类型的交点，称为m 交点镶嵌；三级分类进一步将镶嵌单元限制为正多边形或均匀多面体，即均匀镶嵌（uniform tiling），再按照交点类型和传递集类型（阶数）进行细分，各类型包含有限数量的模式，如平面单交点—1 阶均匀镶嵌的类型只有11 种（不含亚型）；四级分类进一步约束为所有交点、交边和单元均全等，只包含3 种正多边形镶嵌与1 种立方体镶嵌。这种分类能够对基本元素类型进行定量描述、分析和控制，在计算性操作中有重要的应用价值。

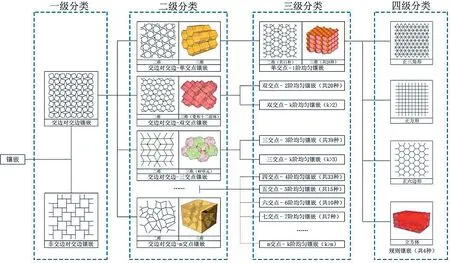
图2： 二维与三维镶嵌的分类和典型图式

格（Lattice）与离散群（Discrete Group）是离散几何的重要研究对象，它们以对称性操作作为数理基础，与晶体结构的关系密切。周期性晶体的基本单元具有同一性，不同的对称分布方式决定了不同的性质。晶体学中将基本单元抽象为点，点的空间分布构成了空间点阵（也称为晶格）。数学上目前证明在二维空间中有5种布拉维格（Bravais Lattice）和17 种离散对称群（图3），三维空间中有14 种布拉维格和230 种离散对称群[12]。它们与镶嵌之间也有密切关系，如由14 种布拉维格子推导出的维格纳—赛茨晶胞（Wigner-Seitz Cell）可构成空间镶嵌，每种镶嵌的基本单元完全相同（图4）。

图3： 平面布拉维格和离散对称群

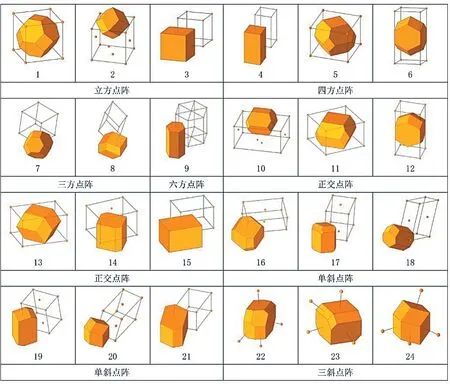
图4： 可构成镶嵌的规则多面体（晶胞）与对应的空间点阵（晶格）

2）关联问题。由两种不同维度的对象以及这些对象之间的单一关系组成的抽象系统称为关联结构。例如在欧几里得平面中，考虑点和线的连接或非连接关系，选择性忽略距离、方向等性质，得到的就是一种关联结构[13]。关联结构可以处理更高维度的对象（n维空间、非欧空间等），而研究最多的还是点—线关联。对设计工作来说，关联结构在空间关系、功能关系、连接关系的研究中有重要价值。

超图（Hypergraph）不限制每条线关联的顶点数量，属于一般性关联结构，其中每条线关联的点数均为K 的超图称为K 阶均匀超图[14]（图5）。2 阶均匀超图称为图（Graph），即每条线只关联两个顶点。图是图论（Graph Theory）的主要研究对象，后者包含著名的“七桥问题”等。根据连接关系可将图单元分为多种类型（图6），如多重图—简单图、定向图—非定向图、平面图—非平面图（在连线不交叉时无法在平面内绘制）、循环图—非循环图等[15]，这些性质对设计工作有重要价值。

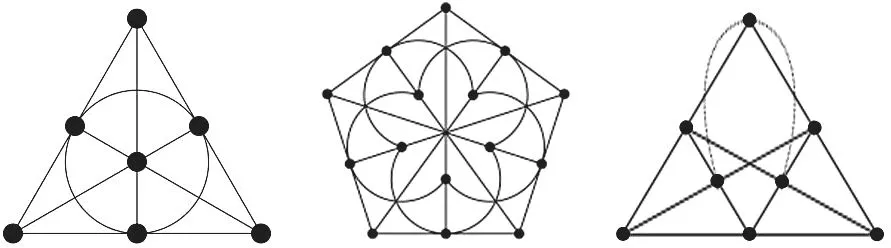
图5： 三种3 阶均匀超图示例（限定直线或者曲线不包含拐点）

图6： 图（Graph）的多种分类

2.与其他几何分支的交叉领域

离散几何与微分几何、拓扑几何、计算几何之间存在广泛的交叉领域（图7），它们拓展了离散几何的研究范畴，从中产生了很多强有力的数学工具。

1）离散微分几何（Discrete Differential Geometry）是离散几何与微分几何的交叉。微分几何是运用微积分工具研究曲线与曲面性质的数学分支。相应地，离散微分几何主要探索平滑曲面的离散等价物的构造方法[16]，以解决曲面的组合建构和计算性问题。对连续对象进行离散化处理也是著名的“有限元分析”方法的理论基础，结构离散后的网格质量直接影响到计算精度。从离散微分的角度，可以将曲面网格区分为共轭网格、正交网格、渐近网格、等温网格等，不同网格有各自的特征和处理优势。离散微分几何首先被应用在计算机图形学的方面，在曲面建模和渲染方面具有重要价值，也广泛应用于机械制造、工业设计、建筑设计、计算解剖学等领域。

2）拓扑组合（Topology Combinatorics）来自离散几何与拓扑几何的交叉。表面看来，拓扑几何与离散几何的研究范畴正好相反，前者主要研究拓扑变换下图形的连续、连通性问题[17]，后者研究离散性问题，但正是在二者向对方转化的领域产生了特别的创新价值。例如拓扑技术在解决著名的组合问题如Kneser 着色猜想中起了重要作用，而离散Morse 理论为拓扑结构可视化、拓扑曲面重构带来了新的解决方案。拓扑组合主要涉及拓扑原理在离散对象上的应用[18]、拓扑对象的组合特征，以及开发拓扑技术处理组合问题及部分图论问题[19]。拓扑原理为离散结构的复杂性变换提供了支持，在形态设计中有重要应用价值。

3）计算几何主要研究几何问题的计算性表达和算法开发[20]，一般分为数值计算几何和组合计算几何两类。其中数值计算几何构成了CAD / CAM 系统的基础；组合计算几何（Combinatorial Computational Geometry）用算法处理几何结构，关注欧式空间中离散对象的算法设计[21]，是计算几何与离散几何的交叉领域。后者包含了建筑师所熟悉的Voronoi 图构造、凸壳计算、三角剖分等，也包含几何查找（检索）、交与并、几何体的排列、形状重建、运动规划等范畴[22]。计算几何的特征在于其工具性而不限于特定的几何对象，建筑界讨论过的“算法几何”大致属于计算几何的范畴。

三、在建筑计算性设计中的应用

1.同维度几何组合与形态设计

镶嵌在建筑中的应用有悠久的历史，只是过去缺乏从数学角度的分析归纳。例如数学家指出，建于12 世纪末的伊朗马拉盖地区的墓塔（Blue Tomb）已经使用了准周期镶嵌图案[23]。在当代建筑设计中，平面镶嵌多用于建筑的表皮设计，空间镶嵌多用于结构形态和造型设计。结构化的表皮设计也常用到空间镶嵌模式，如北京奥运会游泳馆和冰岛HARPA 音乐厅。后者以当地典型的地质构造玄武岩为主题，其基本几何结构属于维格纳—赛茨晶胞中的单斜点阵（图4—18）。该建筑表皮在具有构件统一性的同时，实现了晶莹夺目的晶体效果（图8）。

图8： 冰岛HARPA 音乐厅南立面及表皮设计分析

镶嵌原型的维度转换是设计创新的重要途径。运用计算性设计工具，通过拉伸、折叠、包裹等升维操作和剖切、投影等降维操作，可以快速进行二维与三维转换，生成多种复杂形态。这方面已经有大量的建筑实践案例。

填装与覆盖方面，传统的屋面瓦铺装以及鱼鳞状墙板结构事实上运用了覆盖原理。填装问题与建筑形体的虚实关系处理有一定的共通性，例如最密集球填装问题、立方空间中多种方体的填装等，在当代建筑计算性设计中的应用值得探索。

在基本单元确定的“自下而上”的生成设计中，单元的复制所遵循的对称性均包含于格与对称群揭示的有限类型之中。在这些数学规则的支持下，能够以极小的计算量生成给定条件下的所有形态，对于模式穷举有重要价值。17 种平面对称群已广泛用于传统的建筑装饰和印染图案设计方面，更为复杂多样的空间对称群在三维形态的计算性生成、离散自动化建造[24]方面有较大的应用潜力。

2.关联结构与功能/空间关系图

由于其高度的抽象性，关联结构的应用范围很广，从城市群分析到室内空间布置都有很强的适用性。超图不限制一条边（路径）所关联的节点数量，可用于交通网络设计、路径规划、设施选址等方面。而建筑计算性设计中最常用的还是图（graph），如功能气泡图在数学上属于一种简单图。对建筑空间进行抽象后，往往能发现隐含的逻辑，一个早期的范例是March 等人运用空间图语法（Spatial Graph Grammar）将F.L.赖特设计的三种别墅平面抽象为类似的图解[25]（图9）。

图9： 运用空间图语法（SGG）对F.L.赖特住宅的分析

图论原理可广泛应用于空间生成设计，例如平面图—非平面图可以判定某种空间关系是否能在单层平面中实现；循环图—非循环图、定向图—非定向图可用于不同交通组织模式的性能对比；最小生成树（Minimum Spanning Tree，准确名称应为最小连通树）是寻找一种非循环图，使整个图中所有路径之和最小，多用于交通流线或空间骨架的生成设计。

图论的一些基础参数已在多种空间分析工具中得到应用。例如图论中的度（Degree）是指与一个节点直接相连的边数，在空间句法中称为连接度（Connectivity），在空间设计网络分析（sDNA）和城市网络分析（UNA）中分别称为线性连接度（Line Connectivity）和到达（Reach）；中间中心度（Betweenness Centrality）表示某条轴线或某条街道段位于从任一空间到其他空间的最短路径上的次数，在空间句法中称为选择度（Choice），在sDNA 和UNA 中称为中间度（Betweenness）；而在社会网络分析（SNA）理论中上述参数沿用了图论里的原有名称[26～31]（表1）。在实际应用中，点与线的选择可以根据需要决定，例如将街道作为空间主体而不是连接体进行分析。

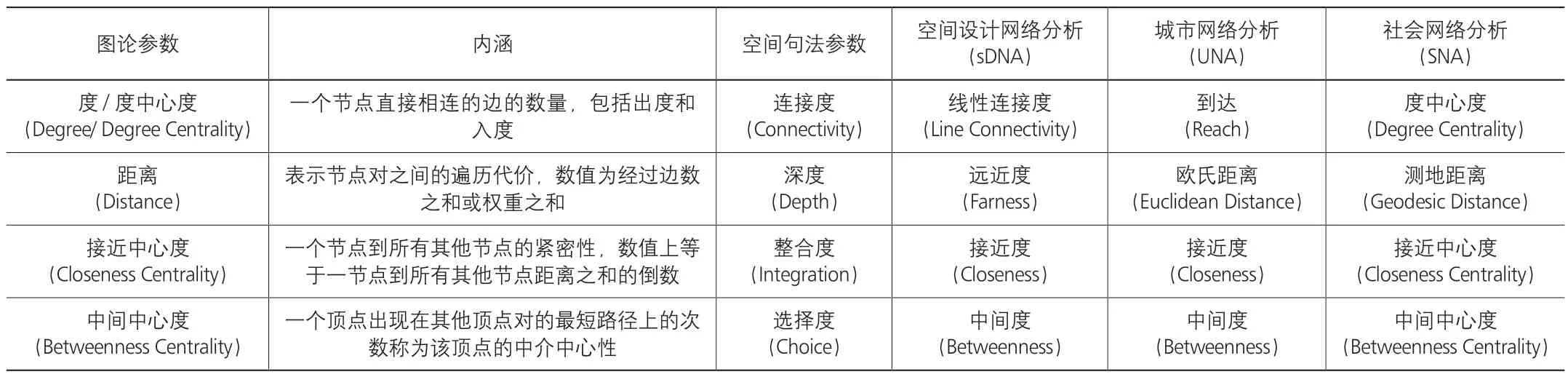
图论与多种空间分析工具的参数对照 表1

3.离散微分与曲面优化

传统的砖石建筑可以看作是一种“离散化”建造方式，而拱是用离散材料形成大跨度空间的力学与几何学选择。离散材料的曲面造型能力可以达到惊人的水平，如20 世纪乌拉圭建筑师E.迪埃斯特（Eladio Dieste）用黏土砖建造的一系列厂房与仓库建筑。当代建筑几何学中，曲面的找形、优化与细分一直是热点研究领域。在离散微分原理的支撑下，建筑师能够进行更为多样化、前沿性的探索。

在曲面形态设计中往往存在找形和优化两种工作类型。基于离散材料的找形逻辑，与基于连续材料（如3D 打印）的逻辑差异很大。ETH的BLOCK研究小组（BRG）2016 年在威尼斯双年展上建造了一个跨度达到16m 的拱壳结构。与A.高迪、F.坎德拉等前辈大师不同，这个拱壳使用了399 块石灰石板（图10），多数厚度为5cm，没有用任何砂浆粘结剂。基于离散微分原理的计算性设计方法—推力网络分析方法（Thrust Network Analysis）代替了20 世纪的“逆吊法”，帮助建筑师找到了只包含压力的拱壳形式及相应的网格细分，消除了所有弯矩，从而使简单开槽拼装的“离散化”建造方式成为可能[32]。

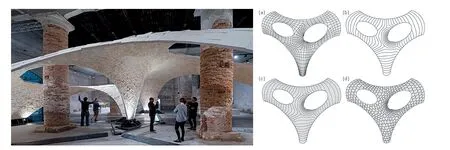
图10： BRG 建造的拱壳结构“犰狳”（左）及基于静力学的曲面细分（右）

曲面幕墙的建造同样需要离散化处理，形态优化和单元细分的质量对造型、施工和造价的影响很大。在构件层面上，将双曲面优化为单曲面、细分曲面为平面、减少构件类型是优化设计的一般原则。虽然常见曲面均易转换为三角单元网格，但这种拟合往往不能反映曲面主方向，每个交点汇集6 条边，节点比较复杂。利用离散微分原理将曲面拟合为平面四边形（Planar Quad）网格是常用的优化方案之一，这种平面单元便于加工，网格整体呈现为双向控制线，且大都沿主曲率方向分布，更能反映几何形体特征。曲面优化是深化设计能力的试金石，例如与早期作品广州歌剧院的石材幕墙相比，ZAHA 事务所近年的澳门Morpheus 酒店等作品在曲面细分和空间整合度上达到了更高的水准。

4.拓扑组合与形态创新

拓扑组合工具在处理几何对象的多样性方面具有突出优势。例如将镶嵌原型和拓扑变换结合起来，能够产生大量新颖的图形群。镶嵌的拓扑变换是一种镶嵌单元连续地变形为另一个无撕裂点的镶嵌模式，在变换过程中原交点的阶数、邻近单元数保持不变；在类型上可以分为基于交点、交边和复合型拓扑变换。根据拓扑分析，可以发现许多直观上毫无关系的镶嵌图形属于拓扑同胚，能够实现连续性变换（图11）。而这些图形的对称类型并未发生变化，提示了从对称群出发进行逆向操作的可能性。

图11： 拓扑同胚的镶嵌图案

基于交点特征的镶嵌图形分类为拓扑变换奠定了基础。以P3 型彭罗斯镶嵌为例，首先根据其7 交点特征，基于核心交点提取7 种基本单元，然后以其他交点相对于核心交点的偏移矢量为连续函数，调节位移量及角度变量生成多种变形模式（图12）。与原图相比，变形后的图形维持了准周期的旋转对称性，但又产生了新的特点，如第3种模式的外观尺度有所膨胀，强化了彭罗斯镶嵌的分形特征。这种拓扑变换操作通过简单的参数控制，生成极为丰富的新形态。类似的操作也可以用于关联结构，在空间布局的生成设计中有较大的应用潜力。

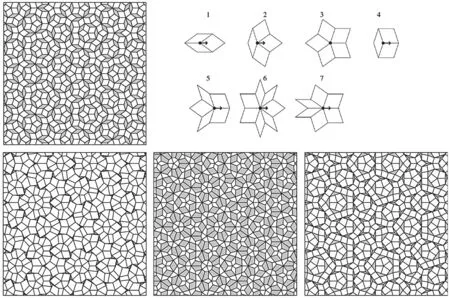
图12： 基于交点性质对彭罗斯镶嵌原型（左上）所做的3 种变换

5.面向离散对象的算法应用

计算几何的算法工具已经渗透到建筑几何学的各个方面。算法的内涵首先是一套可执行的逻辑规则，其次是集成化的编程语言。针对上述离散几何问题，数学领域已开发出大量算法，例如填充问题中的圆球填装可以采用Kangaroo 算法，Grasshopper 平台也有相应插件进行直观模拟；图论中的最小生成树问题，主要有Kruskal 算法（加边法）、Prim 算法（加点法）和破圈法三种算法；离散微分范畴下的形状（曲线和曲面）重建算法在动态建模与优化方面有应用价值；属于临近问题的Voronoi 算法已广泛用于建筑表皮、平面与空间形态的生成设计；运动规划问题的相关算法可用于智能建造中机械臂的可达性与碰撞问题等。这些问题中有不少是开放性的，还没有终极解决方案，只有阶段性的最佳逼近方法。

四、体系化认知与应用

基于以上考察，可初步梳理离散几何范畴下与建筑计算性设计关系密切的内容，总结一般性应用领域（表2）。作为应用基础研究，这种工作并非“发明”一种新理论，而是将既有的、局部性的经验和实践收纳于一个体系化的认知框架内，并启发新的应用可能性。与片段化的认知相比，形成知识体系至少在三个方面具有更大的优势。第一是面对实际问题，有助于快速定位它在数学领域所处的范畴，更快地找到正确的解决途径；第二是数学体系的逻辑严整性有助于设计师运用演绎的方式探索新的应用潜力，例如很容易发现历史经验只触及到了某些局部，数学方面还有更为广阔的领域有待挖掘；第三是有助于通过分支体系之间的联系与交叉，综合多种工具进行设计创新探索。离散几何的上述分支之间存在密切的关联，例如镶嵌的精确分类为拓扑变换奠定了基础，关联结构也关涉网格问题，离散微分可以看作寻求合理镶嵌模式的过程，而几乎所有的领域都越来越依赖算法的支持。

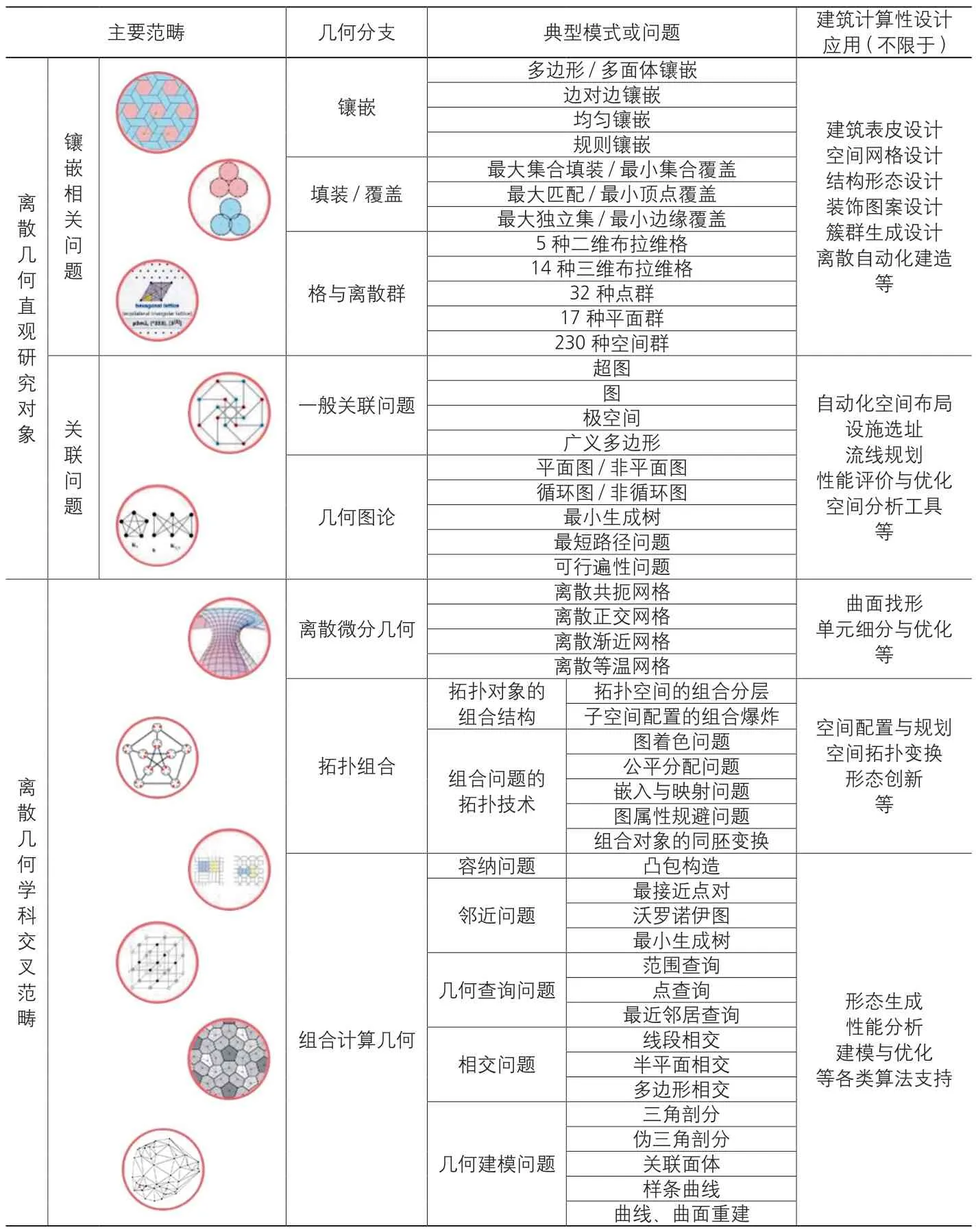
离散几何的对象范畴与一般性应用 表2

在综合运用数学工具进行设计创新方面，SKOPE 事务所设计的布鲁塞尔法语部议会大楼提供了一个简明的例子。大楼的幕墙设计经过分析是提取P3 型彭罗斯镶嵌的交点，再对交点进行Voronoi 运算，得到了由5 种多边形构成的新型图案（图13）。虽然设计者未必从几何体系的角度展开思考，但从数学范畴来看，其创新性在于将算法和镶嵌原型进行结合，用少数模件的组合获得了随机性效果。这种方法论具有一定的普遍性意义。

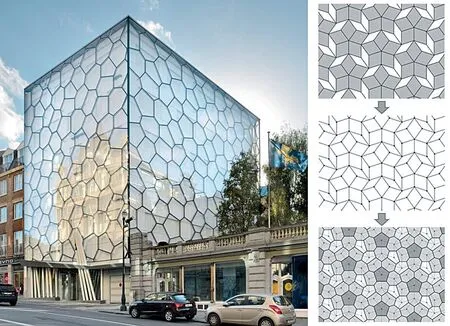
图13： 布鲁塞尔议会法语部办公楼及其表皮生成逻辑分析

五、结语

数字化的逻辑基础之一，就是用离散的点集代替现实对象，从而获得可计算与可操控性。离散几何着重研究的组合问题，在内涵上与建筑计算性设计有深刻的一致性，因此从概念阶段的形态生成、到依据条件进行适应性变换，再到成果的评估、优化乃至装配式与智能化建造等，离散几何原理的应用可以贯穿设计前期、中期和后期的全过程。

在人工智能技术突飞猛进的背景下，建筑设计已经呈现出越来越强的计算性和整合性发展趋势。在方法层面，一方面有基于数据和案例的机器学习，另一方面有基于数理规则的演绎与生成。依托离散几何的数学体系，有助于将片段化的知识和经验整合在一个较为完整、清晰的框架内，探索新的应用范式，从而发挥更大的知识效能。同时跨学科研究也是一项极富挑战性的工作，本文只能基于目前有限的认识，以设计应用为导向初步梳理离散几何的认知与应用体系，这方面的工作还需要今后不断进行修正、完善与提升。

注释

① 多数数学文献中组合几何被认为等同于离散几何，本文采用认知度更高的“离散几何”这一说法，涵盖组合几何的相关内容；还有一些更为抽象的分支如结构刚性与柔性理论和定向拟阵等，因与建筑设计关系不很直接，未纳入本文的讨论；关于几何单体性质的研究与离散几何关系密切，主要包含在“凸体”几何分支下。