Structural Connectivity Enhanced Anisotropic 3D Network for Brain Midline Delineation

Yufan Liu, Kongming Liang, Yinuo Jing, Shen Wang, Zhanyu Ma, Yiming Li,Yizhou Yu, Yizhou Wang, Jun Guo

Abstract: Brain midline delineation can facilitate the clinical evaluation of brain midline shift,which has a pivotal role in the diagnosis and prognosis of various brain pathology.However, there are still challenges for brain midline delineation: 1) the largely deformed midline is hard to localize if mixed with severe cerebral hemorrhage; 2) the predicted midlines of recent methods are not smooth and continuous which violates the structural priority.To overcome these challenges, we propose an anisotropic three dimensional (3D) network with context-aware refinement (A3D-CAR)for brain midline modeling.The proposed network fuses 3D context from different two dimensional(2D) slices through asymmetric context fusion.To exploit the elongated structure of the midline,an anisotropic block is designed to balance the difference between the adjacent pixels in the horizontal and vertical directions.For maintaining the structural priority of a brain midline, we present a novel 3D connectivity regular loss (3D CRL) to penalize the disconnectivity between nearby coordinates.Extensive experiments on the CQ dataset and one in-house dataset show that the proposed method outperforms three state-of-the-art methods on four evaluation metrics without excessive computational burden.

Keywords: brain midline delineation; refinement network; structure prior; connectivity regular loss

1 Introduction

The human brain in healthy individuals is naturally bilateral symmetrical and divided into the left and right hemispheres which are separated by a natural midline on the axial plane of Computed Tomography (CT) images.However, different types of pathological conditions, especially traumatic brain injuries, strokes, and tumors,could lead to higher intracranial pressure (ICP).High ICP has a potential effect on the brain parenchyma by pushing the cerebral hemisphere from one side to the other side, which directly causes the ideal midline (IML) to be distorted to the deformed midline (DML), as shown in Fig.1(a).This phenomenon is called midline shift (MLS) [1].

The degree of MLS can serve as a quantitative indicator for physicians to make the diagnosis, develop treatment plans and predict treatment outcomes [2].For example, the likelihood of performing brain surgery is proportional to the degree of MLS [3].Specifically, the Brain Trauma Foundation (BTF) recommended emergency surgery for any traumatic epidural, subdural, or intracerebral hematoma causing an MLS larger than 5 mm in its guidelines [4].Therefore, brain midline delineation plays a vital role in timely disease diagnosis and monitoring, which helps doctors to understand patients’ medical conditions.

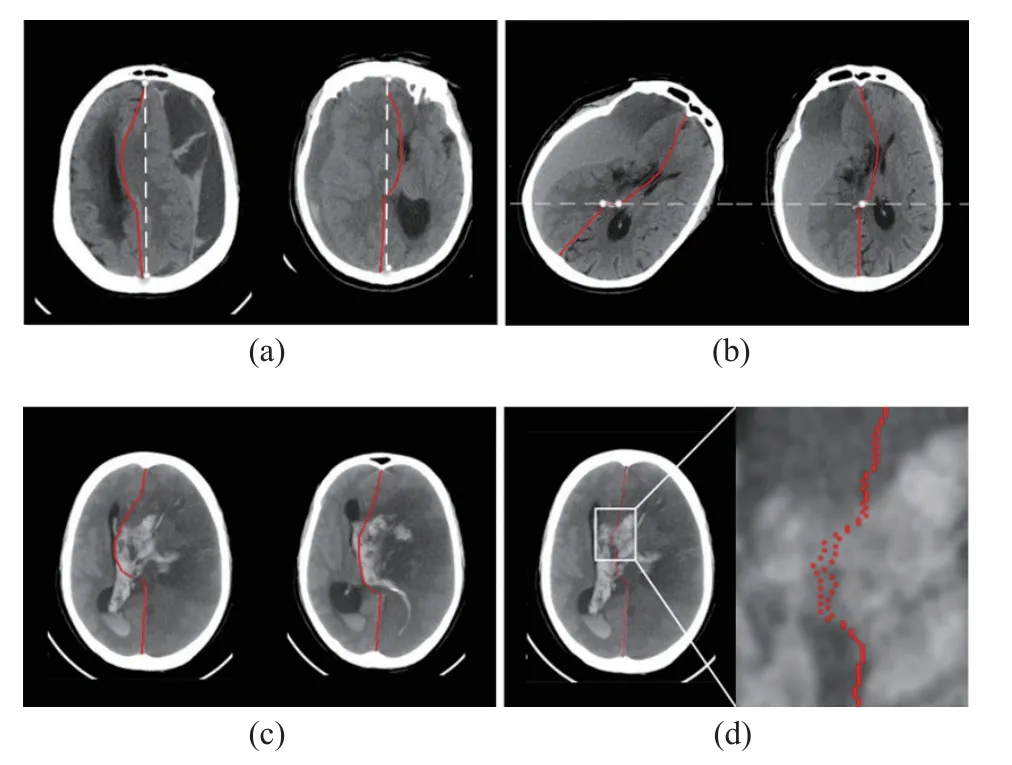
Fig.1 Different conditions of midlines: (a) examples of ideal midlines (IML, white dotted line) and deformed midlines (DML, red line) on head CT images; (b) examples of the brain pose that does not satisfy the prerequisite of regression-based methods and standard brain pose; (c) an example of the largely deformed midline mixed with severe cerebral hemorrhage; (d) an example of the predicted midline, which violates the structural prior

In clinical applications, doctors detect MLS in various ways.The most prominent measurement is done by a CT scan and the CT Gold Standard is the standardized operating procedure for detecting MLS [5].However, since the physiological and pathological morphologies of midline structure are very complex [6], midline delineation on CT images is time-consuming and shows inter-observer variation.Therefore, computer-aided brain midline delineation algorithms are valuable for their significant potential to decrease human cost, improve accuracy and reduce individual discrepancy.

Current methods for brain midline delineation can be divided into two parts, traditional methods [7–10] and deep learning-based methods [11–14].Traditional methods are mainly based on anatomical markers and symmetrical models,which are only effective for images with a relatively normal midline.In the cases with the largely deformed brain, these methods are often unsatisfactory, because the predefined anatomical points are hard to localize and the soft-tissue contrast is relatively low.Deep learning-based methods can compensate for the shortcomings of traditional methods.They usually formulate the midline delineation as a regression problem.The regression-based methods [11, 12] all assume that there is at most one horizontal coordinatexof midline pixel for each vertical coordinatey.However, this assumption may fail in some extreme poses of the brain.

Most of the recent deep learning-based methods ignore the differences among this task and other medical image recognition or segmentation tasks.They use general networks for feature extraction which are not well designed for the special structural properties of the midline.First, the brain midline is a smooth and continuous curve.Thus, the coordinates of two adjacent brain midline pixels should not differ too much.Second, the structure of the brain midline is elongated, which makes it indispensable to have a larger receptive field in the vertical direction and avoid redundant information in the horizontal direction while feature extracting.In addition,the contextual information across slices is helpful for midline delineation.Qin et al.[14] have studied the detection of three dimensional (3D)brain midline.They used 3D U-Net for feature extraction and considered the effect of a cerebral hemorrhage on midline detection.However, the CT images used in daily clinical practice have a lower resolution in thez-axis direction than in thex,y-axis directions.This anisotropic data is called 2.5 D data [15].The low resolution in thez-axis direction tends to cause overfitting of the 3D network.Therefore, current midline delineation methods are not well designed for the 2.5 D data with a volumetric nature but inter-slice discontinuity characteristic [16].

To address the aforementioned problems, we propose an anisotropic 3D network with contextaware refinement which contains three parts: preliminary feature extraction, context-aware feature refinement, and anisotropic feature learning.In the preliminary feature extraction part, we introduce asymmetric 3D context fusion strategy [17] into plain two dimensional (2D) U-Net [18]to model the context of different 2D slices.In the context-aware feature refinement part, we refine the feature map of each scale to extract more discriminating features.In the anisotropic feature learning part, an anisotropic block is specially designed for objects with anisotropic structural properties such as the midline, and focuses more on the difference of midline in thexandydirections.At the same time, we introduce a novel 3D connectivity loss to penalize predicted brain midlines that are not continuous, as shown in Fig.1(d).To satisfy the assumptions of the regressionbased approach, we propose a lightweight pose alignment module based on Residual Network(ResNet)-18 [19] to ensure that at most onexcoordinate corresponds to eachycoordinate of the input brain midline coordinates.In summary,our main contributions are as follows.

1) We propose an anisotropic 3D network with context-aware refinement (A3D-CAR) to model inter-slice information and leverage more anisotropic context for modeling the midline structure.

2) A novel 3D connectivity regular loss (3D CRL) is proposed with structural priority to guarantee the connectivity of the predicted midline.

3) We propose a pose alignment module for adjusting the pose of the brain in the CT image to standard one so that the midline meets the preconditions of the regression method which will improve the flexibility of our model to different brain poses.

4) Our method is validated on the CQ dataset and a larger in-house brain dataset.The experimental results show that our method outperforms the other comparison methods with no excessive computational burden.

A preliminary version of this work has been reported [20].Compared to the preliminary work,this work introduces some critical extensions.Firstly, the proposed method introduces an asymmetric 3D context fusion strategy into plain 2D U-Net to model the context of different 2D slices while the preliminary work only focuses on 2D midline data.Secondly, in terms of loss functions, the proposed method introduces the continuity loss in thez-direction to guarantee the connectivity of the predicted midline.The preliminary work only considers the continuity loss in they-direction.Thirdly, to exploit the elongated structure of a brain midline, the proposed method designs an anisotropic module that balances the difference between the adjacent pixels in the horizontal and vertical directions.

2 Related Works

2.1 Brain Midline Delineation

The current brain midline detection methods mainly include two parts: traditional methods and methods based on deep learning.Traditional methods for midline delineation can be classified into two types: landmark-based ones [7, 8] and symmetry-based ones [9, 10].For example, [7]proposed an automatic algorithm to estimate the midline position from CT images, using multiregion shape matching based on matched feature points.[8] proposed an automatic model, and quantified the midline shift by selecting candidate points.[9] separated the midline into three segments, and the middle curve section was represented by a quadratic Bezier curve fitted with symmetry.[10] proposed to estimate the midline shift caused by cerebral glioma based on the enhanced Voigt model and local symmetry.These traditional methods have made important contributions to brain midline delineation, but they often fail in some cases with large deformation due to the relatively low degree of soft-tissue contrast on CT images and the great difficulties in locating pre-defined anatomical points or parts.

Recently, many methods based on deep learning [11–13] have performed well in brain midline detection.[11] viewed midline delineation as a regression task, which initially located the region of the midline by extracting high-level and low-level semantic information, and then refined the location of the midline using regression.[12] presented a dual-head mechanism based on limit head and regression head.The limit head was used to detect the vertical extent of the brain midline, and the regression head was used to locate the pixel coordinates of the brain midline.However, in regression-based methods, it is generally believed that there is only onexcoordinate corresponding to eachycoordinate on the midline which may fail in some CT images with extreme brain poses.[13] considered the delineation of the brain midline as a segmentation task, and a three-stage framework is established.However, their method can not be trained endto-end which is sub-optimal.

2.2 Volumetric Context Fusion for 2.5 D Data

The resolution of brain midline datasets varies considerably in thex,y, andzdirections, and the processing of this type of 3D medical data,which is called 2.5 D data [15], has recently attracted increasing attention.Although 2D networks are relatively well developed, they can not effectively model 3D information.The midline delineation method proposed by Qin et al.[14]has taken into account the importance of 3D information and directly used 3D neural networks to learn 3D information representation.However, the resolution of the midline dataset is usually higher in thexandyaxis and lower in thezaxis.3D neural networks [21–23] do not differ in their feature extraction strategies in the horizontal and vertical planes, which is likely to lead to severe overfitting in the vertical plane.Recently, some approaches introduced axial convolutions [24–26] or shifting adjacent slices [27, 28]to learn 3D representations.Some works for lesion detection [17, 28] have constructed 3D-like networks by introducing inter-slice information fusion methods to 2D pre-trained neural networks.These works combine both 2D and 3D representation learning to process 2.5 D data.

2.3 Anisotropic Feature Learning

The elongated structure is an important characteristic of the brain midline.Some objects have a similar structure to it, such as the spine, road,lane line, crack, etc.The detection of objects with this structure requires more anisotropic context.Many works [29–33] have been designed specifically for anisotropic feature learning.For example, [29] presented a shape-aware segmentation approach for cervical spondylotic myelopathy segmentation which allowed backbone networks to aggregate both global and local contexts as well as efficiently capture long-range relationships.[30] presented a long-range contextaware road extraction neural network (LR-Road-Net) and used strip pooling to capture the longrange context in both horizontal and vertical directions.[32] performed strip pooling on feature maps of various sizes and applied the multihead attention mechanism to fuse the features produced by strip pooling for remotely sensed road detection.[31] suggested streak-aware pooling to integrate local contextual information to improve lane recognition feature extraction.[33]proposed a novel automatic network for crack detection.This network consisted of a mixed pooling module and a feature attention module.Vertical pooling, horizontal pooling, and average pooling were the three parts of the mixed pooling module to capture long-range contextual dependence.These novel designs are particularly effective for elongated object detection, which are also instructive for brain midline delineation.

3 Methods

3.1 Overview of Network Architecture

As shown in Fig.2, the proposed network consists of three parts: pose alignment, probability map generation, and coordinate regression.Firstly, a pose alignment module is proposed to transform an imageIsinto its aligned imageIathrough a lightweight convolutional neural network.Secondly, the proposed A3D-CAR takes the center-cropped image ofIaas input to obtain the segmentation probability mapYˆpand the midline coordinate rangeYˆlby limit head [11].Finally, the regression head [12] is used to estimate the midline coordinatesYˆlfromYˆp.Moreover, we propose a 3D connectivity regular loss to penalize the discontinuous part of the midline.

3.2 Pose Alignment Module

When a patient is placed on the CT scanner, the distance and angle between the patient and the gantry may cause the pose in CT images to deviate from the standard one.As shown in Fig.1(b),for some extreme poses, the prerequisites of many previous regression-based methods [11, 12] no longer hold.In other words, for each rowyof a CT image, there may be more than one horizontal coordinatexcorresponding to the brain midline.

To solve the above problem, we presented a pose alignment module to extract the affine transformation matrix between the original image and the standard one.As shown in Fig.2, we first obtained the two connection points,P1andP2, between the ground truth midline and the skull in the original imageIs.A straight line connecting these two points was used to calculate the center of the brain and the rotation angle.After that, we applied an affine transformation to the original image and generated its aligned image as ground truth.For training, we used a lightweight network named ResNet-18 [19] as the backbone ofϕ(·) and used the mean square loss(L2 loss) to measure the difference between the prediction and the ground truth image.During inference, the output ofϕ(·) contains three parameters (tx,ty,θ) of the affine transformation matrix.Finally, the original image is transformed to an aligned imageIaaccording to

whereθrepresents the rotational angle andtxandtyrepresent horizontal and vertical displacements respectively.G(·) denotes the standard grid function, andB(·) denotes the bilinear interpolating function.

3.3 Anisotropic 3D Network with Context-Aware Refinement

The normal part of a brain midline is usually easy for the model to delineate.However, the shifted part of a largely deformed midline is hard to identify, since the midline is mixed with large hemorrhage areas, as shown in Fig.1(c).To address this issue, it is highly desirable to develop an efficient network that can leverage more contextual information for modeling the midline structure.In addition, because the structure of the midline is an elongated curve, more contextual information should be considered along they-axis (vertical) than thex-axis (horizontal).

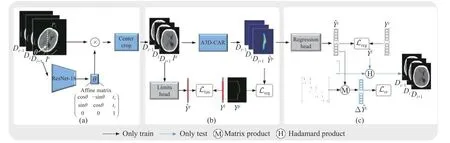
Fig.2 The illustration of the pipeline of our proposed method for brain midline delineation where the proposed pipeline consists of three parts: (a) pose alignment; (b) probability map generation; (c) coordinate regression

As shown in Fig.3(a), we proposed an anisotropic 3D network with context-aware refinement for probability map generation.The whole process can be divided into three parts:preliminary feature extraction, context-aware feature refinement, and anisotropic feature learning.The input 3D image is fed into a preliminary feature extraction network and contextual information of adjacent slices is modeled by slice fusion convolution, after which the preliminary features are cascaded by the extra convolution blocks and a Squeeze-and-Excitation (SE) block to extract more discriminative feature information.Finally,an anisotropic block is designed and added at the end of each layer to expand the respective field while avoiding contaminating information from adjacent regions.In the preliminary feature extraction part, we used 2D U-Net as the backbone and introduced asymmetric 3D context fusion strategy [17] to model the contextual information among different 2D slices.In the contextaware feature refinement part, we attached a feature refinement module that can enhance features of each scale and adaptively integrate them to explore more discriminative ones.In the anisotropic feature learning part, we replaced the original convolution and pooling operations of the feature refinement process with their anisotropic counterparts.The proposed anisotropic operations can emphasize the different importance of context information along the horizontal and vertical directions.

3.3.1 Preliminary Feature Extraction

Fig.3 The illustration of the pipeline: (a) anisotropic 3D network with context-aware refinement; (b) slice fusion connection; (c)anisotropic block

For a standard head CT scan, the slice thickness is typically thick (e.g.5 mm).To model the contextual information of adjacent slices, we introduced the strategy of asymmetric 3D information fusion [17] to the plain U-Net.As shown in Fig.3(b), a slice is connected with allNslices by applying different weights between slices.The experimental results showed that this approach outperforms the 2D approach without introducing excessive computational effort.The architecture gracefully addressed the problems that 2D networks ignore the volumetric contexts and 3D networks suffer from heavy computational costs.Mathematically, for a given 3D input featureE ∈RC×D×H×W, we design an asymmetric fusion weightP ∈RD×D×Cto model the correlation between all the slices in a full connection way.Then the output feature can be obtained as

where · denotes matrix multiplication.EcandPcdenote the feature and weight on thecth channel respectively.

3.3.2 Context-Aware Feature Refinement

As shown in Fig.3(a), we refined each scale of the preliminary feature by applying extra convolution blocks to extract more detailed feature information.To balance the effect and speed, we add more convolution blocks in deeper layers.As shown in [34], the SE block uses global information to model the interdependences among different channels of features, selectively emphasizing the features that are more informative for the results and ignoring those that are less useful.It can ultimately enhance the quality of the representation generated by the network.In addition,the SE block is lightweight, causing a small computational burden.Therefore, we also add SE blocks as channel attention in each layer to extract more discriminative features.

To expand the respective field while avoiding contaminating information from adjacent regions, an anisotropic block is added at the end of each layer.The details of the anisotropic block will be described in the following section.Finally,the refined representation is generated by combining representative features from multiple levels using bilinear interpolation upsampling, concatenating, and one basic convolution block.Compared with the initial feature map output by the backbone, U-Net, the refined features have a larger receptive field and more discriminative anisotropic contextual information.

3.3.3 Anisotropic Feature Learning

Since the midline is a large spanning part of the whole CT image which almost fills up the entire image in the vertical direction, a large receptive field is critical for its delineation.However, many methods for long-range context modeling and expanding receptive field, including dilation convolution [35–39] and global pooling [35, 37,40–43], have the same drawback, which means they all extract or pool features within a fixed square window.This makes the network insensitive to anisotropic contextual information that is critical for the delineation of objects with elongated structures like the brain midline.To address this problem, we introduce an anisotropic block that can allow for a large receptive field in one direction and avoid irrelevant information in the other direction.

The anisotropic block replaces the traditional convolution and pooling with their anisotropic counterparts.Instead of using square windows, the proposed block performs the above two operations with an anisotropic window to emphasize the different importance of context information along the horizontal and vertical directions.Mathematically, for an input featureF ∈RC×H×W, a spatial extent of convolutiong(·)is defined as (h×1) or (1×w).The output tensor obtained by the vertical convolution block can be expressed as

wherei,jmeans the position of the pixel point.(i,j) denote the coordinates.Similarly, the output tensor obtained by the horizontal convolution block can be expressed as

The vertical and horizontal pooling procedures are then performed correspondingly.The output tensor obtained by the vertical pooling window (h×1) is represented as

Similarly, the output tensor obtained by the horizontal pooling window (1×w) can be expressed as

Anisotropic convolution and pooling improve the flexibility of traditional operations by imposing different receptive fields along each direction.Therefore, they can access long-range contextual information in one direction and focus on local detailed information in the other direction.This helps the network to efficiently model the structure of the midline which is an elongated curve.Next, we will introduce the specific details of the anisotropic block consisting of the proposed anisotropic convolution and pooling.

Inspired by the idea of strip pooling module[44], we proposed the anisotropic block to help the backbone network extract the detailed local features and long-range context simultaneously.As shown in Fig.3(b), we feed an input tensorF ∈RC×H×Winto three parallel paths, one of which is a typical convolution operation to generate the featureFs ∈RC×H×W, while the others contain horizontal and vertical convolution and pooling operations, respectively.Then we applied a one-dimensional convolution to modulate the current location feature and its nearby features to getFh ∈RC×H×1andFv ∈RC×1×W, and finally fused these two parts to get the global featuresFa ∈RC×H×Was follows

where Scale(·,·) represents element-wise multiplication,σis a sigmoid function andC(·) is a1×1 convolution.

In contrast to square convolution and pooling, anisotropic convolution and pooling consider narrow and long regions from the horizontal and vertical range, avoiding the connection between two remote regions that are not related to the whole feature map, which can decrease the computation effort.Since a pixel-by-pixel multiplication operation is used in this block, it is basically equivalent to an attention mechanism that weights the importance of pixel points according to horizontal and vertical features.This attention-mechanism-like module is well suited for the brain midline delineation since leveraging more anisotropic contextual information is of vital importance for midline structure modeling.

3.4 Loss Function with Structural Connectivity Prior

3.4.1 3D Connectivity Regular Loss

Since many previous methods [11, 34] considered the brain midline delineation as a regression problem, mean square error (MSE) loss is largely adopted as the loss function.However, the regression-based studies ignore the structural connectivity prior that the brain midline is a continuous curve.To address this issue, we proposed a novel 3D connectivity regular loss to prompt that the predicted midline remains continuous.

For the brain midline, its coordinates in two adjacent rows do not differ significantly.Specifically, we first gave the definition ofδconnectivity.Given a brain CT imagex ∈RH×W,in the range of brain midline, each vertical coordinateyicorresponds to a brain midline horizontal coordinatexi, andX=(x0,x1,...,xn)Tis the set of all brain midline horizontal coordinates in order.If |xi-xi-1|≤δhold eachxi(i=1,2,...,n), we claim that the setXof midline coordinates satisfies ∆-connectivity.Then we denote∆X=(0,∆x1,∆x2,...,∆xn)T, where∆xi=(xixi-1) fori=1,2,...,n.The calculation of ∆Xcan be written as

whereΦis the transformation matrix.

To ensure whether the predicted midline coordinatesYˆcsatisfyδ-connectivity, we define the connectivity regular loss (CRL) as the penalty of the disconnectivity between adjacent coordinates.Considering the three-dimensionality of the brain midline data, we calculate the continuity loss in bothyandzdirections.The specific calculation is as follows

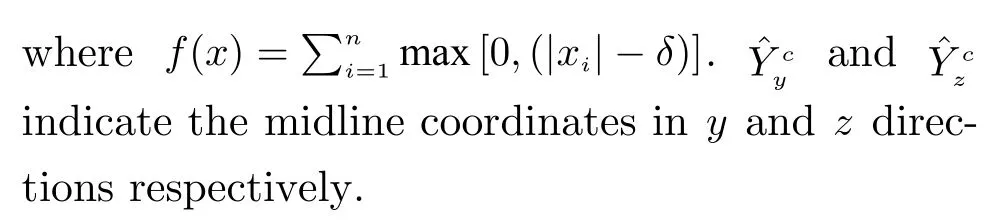
3.4.2 Loss Function

There are four parts of our loss function.In the processing of extracting the vertical range of midline, the loss functionLlimrefers to the binary cross-entropy loss of the limitYˆl.In addition, to generate the segmentation probability map, the cross-entropy loss is also included in the proposed method.We usedLsegto denote the weighted cross-entropy loss of the segmentation probability mapYˆp.In the regression part,Lregis referred to as the mean absolute error loss (L1 loss) of midline coordinateYˆc.Lcris the 3D connectivity regular loss as defined in Eq.(10).Finally, the total loss function is as follows

whereλ,γ,ξandµdenote the weights of each loss component to balance the influence of different parts.

4 Experiments

4.1 Datasets

Our method is evaluated on two brain midline datasets: CQ dataset and a larger in-house dataset.

4.1.1 CQ Dataset

The CQ 500 dataset is a publicly available dataset used for clinical validation.The CQ dataset is a subset of the CQ 500 dataset, which consists of 126 CT series containing an equal number of midline shift samples and normal ones.This dataset essentially covers most cases of midlines.The average MLS is (7.36±5.17) mm and 56% of the samples have significant midline shifts(MLS ≥ 5 mm).

4.1.2 In-House Dataset

Our in-house dataset is labeled by professional physicians according to the gold standard for a midline.It consists of 203 CT series with different degrees of MLS caused by cerebral hemorrhage.The mean MLS is (11.26±6.05) mm and 82% of the samples have a significant midline shift (MLS ≥ 5 mm).

In the data pre-processing stage, each CT slice is resampled to uniform resolution (0.5 mm ×0.5 mm).For both datasets, a total of 9 CT slices with the largest brain area in each subject were selected for experiments.To reduce the computational burden, we split the nine slices into three groups, with each group containing three adjacent slices.Then the slices are fed into the pose alignment module to obtain standard ones.The image is center-cropped to 304 × 400 for the CQ dataset and 336 × 400 for the in-house dataset.We randomly divided the data into 76/20/30 and 120/53/30 as train/validation/test sets.

4.2 Implementation and Evaluation Details

Our network is implemented with PyTorch [45].We use Adam as the optimizer for model training by settingβ1= 0.9,β2= 0.99.The poly learning rate policy is adopted with an initial learning rate of 1e-3.We set the total number of epochs to 200 to allow the model to converge.In Eq.(11), we setλ=γ=ξ=1 andµ=0.5.Since the resolution of thez-axis is much lower than thex-,y-axis for a standard CT scan of the brain, the marginδyandδzin Eq.(10) are set to 1 and 35, respectively.We use four metrics to measure the various midline delineation methods,including line distance error (LDE) [12], max shift distance error (MSDE) [12], hausdorff distance (HD) [13], and average symmetric surface distance (ASD) [13].

4.3 Comparisons to State-of-the-Art

We gave qualitative and quantitative comparisons to the four state-of-the-art midline delineation methods: regression-based line detection network (RLDN) [12], Pisov et al.[11], midline detection network (MD-Net) [13] and contextaware refinement network (CAR-Net) [20] on both our in-house dataset and the CQ dataset.For a fair comparison, all of the experiments are conducted by using the aligned imageIaas input.At the same time, we compared the results with the latest segmentation model UNeXt [46],which was proposed in Medical Image Computing and Computer Assisted Intervention Society(MICCAI) 2022.The results show that the traditional segmentation model was not ideal for the midline task, so the midline depiction can not be considered as a traditional segmentation task.It is worth further thinking through how to better extract the midline slender structure.

4.3.1 Effectiveness Evaluation

As indicated in Tab.1, our proposed model outperforms all four other methods in four evaluation metrics on both datasets which means good generalization capabilities and potential usefulness of our method.As shown in Fig.4, the midline delineated by our method is more accurate than those delineated by other methods.It is not only accurately positioned, but also smoother and more continuous in line with the structural properties of the midline.It can be inferred that our method has strong potential to give a more accurate clinical diagnosis of the pathological large shift of midline.

4.3.2 Model Complexity

Compared with the previous state-of-art 2D midline delineation methods, our method can fuse the information of adjacent slices to achieve a 3D network-like effect without excessive computational burden.Therefore, our proposed methodcan be efficiently applied in practical clinical applications.

Tab.1 Quantitative results on the in-house dataset and CQ dataset

Fig.4 Qualitative comparison between: (a) input; (b) RLDN; (c) Pisov et al; (d) MD-Net; (e) baseline; (f) CAR-Net with 2D CRL;(g) A3D-CAR with 3D CRL; (h) ground truth showing three examples of the midline delineation

4.4 Ablation Study

4.4.1 Effect of Anisotropic 3D Network with Context-Aware Refinement

To verify the effectiveness of the asymmetric 3D information fusion (A3D) and the anisotropic block (ANI) in our proposed network, we conducted ablation experiments for each component on our CQ dataset and in-house dataset.As shown in Tab.2, both A3D and ANI play vital roles in the brain midline delineation on both datasets, and they are also lightweight without causing a large computational burden.

The effectiveness of A3D-CAR has also been verified by conducting ablation studies with or without 3D CRL.The results are shown in the last four rows in Tab.1.Compared to the baseline model, A3D-CAR with 3D CRL performs the best in terms of four evaluation metrics on both datasets.This demonstrates that 3D CRL plays an important role in A3D-CAR.As shown in Fig.5, the segmentation probability map generated by A3D-CAR is more accurate than those generated by the baseline model and CAR-Net,especially for largely deformed midlines.

4.4.2 Effect of 3D Connectivity Regular Loss

We conducted experiments using the baseline model and A3D-CAR to verify the effectiveness of the proposed 3D CRL.The last four rows of Tab.1 clearly show that the model with 3D CRL performs better than the model without it, especially in the MSDE and HD metrics, indicating that the proposed 3D CRL can greatly minimizethe maximum shift error.Moreover, during the inference stage, the 3D CRL of the predicted midline can be used as a connection indicator to confirm the structural connectivity’s performance.Taking the CRL in they-axis direction as an example, the connectivity indicator of the model with CRL is much smaller than the equivalent without CRL, as shown in Tab.3.In conclusion, the proposed 3D CRL may significantly improve the midline structural connection.Fig.6 shows several qualitative comparisons that further confirm the 3D CRL’s efficiency.

Tab.2 Experimental results of the ablation experiments of A3D and ANI

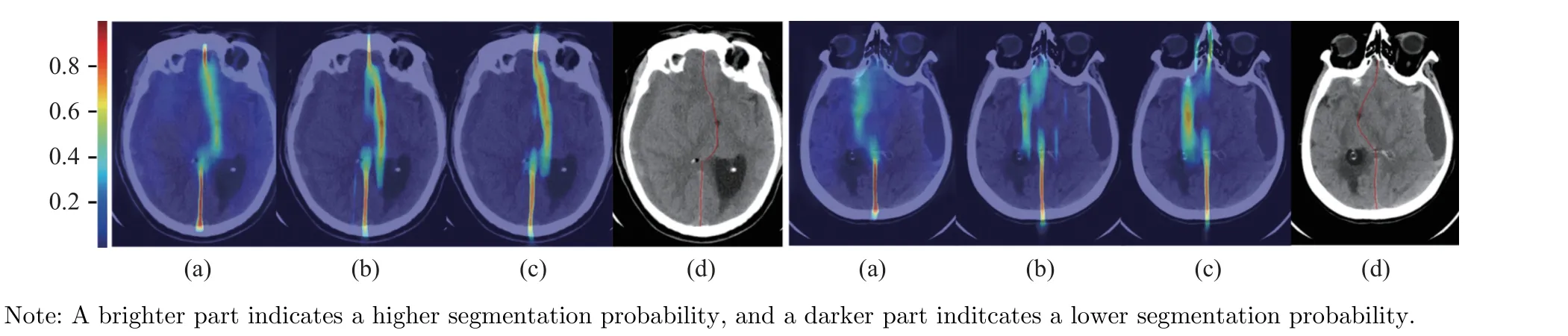
Fig.5 Qualitative comparison results of segmentation probability maps generated by: (a) baseline model; (b) CAR-Net [20]; (c) ourproposed A3D-CAR; (d) ground truth

4.5 Evaluation of A3D-CAR with Significant Midline Shift

Significant midline shift indicates that there may be severe infarction, hemorrhage, tumor, or inflammation, which needs emergency surgery.Therefore, accurately delineating significant midline shift is of vital importance in clinical routine.Due to large deformation, the predefined anatomical points or parts may not be visible.So it is more challenging to accurately delineate the midline with a significant shift than a normal one.In order to evaluate the robustness of the proposed A3D-CAR on the significant midline shift delineation, we selected the images with severe midline shift (MLS ≥ 5 mm).Quantitative segmen-tation results on the two datasets are summarized in Tab.4.Referring to the results in Tab.1,we can see that the performance of all models decreases on the significant midline shift delineation.For example, the LDE of the proposed A3D-CAR (w CRL) increases to 1.34 from 1.16 and 1.07 from 0.87 on the in-house dataset and CQ dataset respectively.This further indicates the difficulty of significant shift midline delineation.Even so, our proposed method can still achieve the best performance, since the proposed slice fusion strategy can learn the contextual information of adjacent slices and effectively model the character of a significant midline shift.

Tab.3 Quantitative results of the connectivity indicator of the midline generated in terms of mean (std)

Fig.6 Qualitative comparison between: (a) A3D-CAR with 3D CRL; (b) A3D-CAR without 3D CRL; (c) ground truth

Tab.4 Quantitative results on the in-house dataset and CQ dataset with significant midline shift

4.6 Evaluation of Generalization Ability

The generalization ability of a method is crucial for its application in clinical routine, since the images may come from different devices or institutions.To evaluate the generalization ability of the proposed A3D-CAR, we used the model trained on the CQ dataset to process the images from the in-house dataset.Both the CQ dataset and the in-house dataset are composed of CT images, including a certain number of midline shift samples and normal ones.Compared with the CQ dataset, the midline shift in the in-house dataset is more complex and difficult to delineate.As shown in Tab.5, our proposed A3DCAR outperforms the other methods in terms of four evaluation metrics, especially in the MSDE and HD.It demonstrates that our proposed A3DCAR can serve as a universal model and well generalize across different datasets.

Tab.5 Generalizability evaluation of A3D-CAR compared with different methods trained on CQ and tested on in-house

5 Conclusion

In this work, we proposed an anisotropic 3D network that incorporates context-aware refinement and structural connectivity prior for midline delineation.The proposed network gracefully exploits the inter-slice information and the anisotropic context of the midline structure.To increase the continuity of the predicted midline,a novel 3D connectivity loss is presented by penalizing the distance between adjacent midline coordinates.In addition, we introduced a pose alignment module for standardizing the pose of a head CT image to match the preconditions of the regression-based methods.We evaluated the proposed method on the CQ dataset and an in-house dataset.Experimental results show that our proposed method outperforms three state-of-the-art algorithms without excessive computational burden.The qualitative result shows that the predicted midline of our proposed method is more smooth and accurate than other comparison methods.Moreover, the proposed method has better generalization ability than the other comparison methods.