固化降温工艺对固体发动机药柱温度场和结构完整性的影响①

2023-11-14鲍福廷郭颜红惠卫华伍永慧王鑫鑫

固体火箭技术 2023年5期

洪东,鲍福廷,郭颜红,惠卫华, 伍永慧,王鑫鑫,常恒

(1.西北工业大学航天学院,西安 710072;2.西安北方惠安化学工业有限公司,西安 710302)

0 引言

固体火箭发动机药柱从生产到服役要经历固化降温、低温试验及长期存储等过程,此期间会与环境不断发生热交换,并产生不均匀温度场,使发动机药柱承受热载荷作用,同时由于推进剂的热膨胀系数一般比壳体大一个数量级,导致药柱及各粘接界面产生较大的热应力,影响发动机药柱的结构完整性和使用可靠性[1]。发动机药柱固化降温后的热应变始终存在于整个生命周期[2],因此准确分析评估热应力的影响,对发动机药柱结构完整性分析及寿命预估都具有重要意义。

针对热载荷引起的发动机药柱结构响应问题,传统的方法是将温度场简化为均匀温度场[3-5],采用热力耦合分析方法计算瞬态传热过程中药柱内部的结构响应。文献[6-11]则考虑了不均匀温度场引起的结构响应,CHYUAN[12]和LIU等[13]考虑了非稳态热载荷环境条件对药柱内部温度场及结构完整性的影响,文献[14-16]考虑了对流换热系数对发动机药柱结构响应的影响,但上述方法均未考虑对流换热系数与壳体壁温及环境温度的耦合变化。而在实际的降温过程中,发动机药柱主要通过壳体与外界进行热交换,壳体表面的对流换热系数受到对流状态、表面温度、空气特性、环境温度等因素影响,并随着壳体壁温的降低及外界环境温度的改变而不断变化[17],因而不同的降温工艺参数会导致壳体表面对流换热系数的差异,进而对降温后的药柱性能产生影响。因此,准确分析计算固化降温过程热载荷引起的发动机药柱结构响应,研究降温工艺对发动机药柱性能的影响,应充分考虑对流换热系数与壳体壁温及环境温度的耦合关系。

本文采用有限元分析方法对固化降温过程进行数值模拟,通过编写FILM子程序实现对流换热系数与壳体壁温及环境温度的耦合计算,同时考虑热辐射的影响,极大提高了降温过程的仿真精度,基于此研究了不同的固化降温工艺对某碳纤维壳体发动机药柱的温度场和结构完整性的影响,旨在进一步准确预估固化降温过程中药柱的温度及应力应变情况,为优化碳纤维壳体药柱降温工艺、提高药柱结构完整性安全裕度提供理论指导。

1 热力耦合计算模型

1.1 瞬态热传导有限元方程

瞬态温度场的场函数温度不仅是空间域Ω的函数,而且是时间域t的函数[18],建立三维瞬态热传导温度场有限元方程的一般格式:

(1)

将空间域Ω离散为有限个单元体,在典型单元内温度列阵φ可近似用结点温度φi插值得到,再通过有限元求解方程(式2)确定n个结点温度φi:

(2)

1.2 对流换热系数计算模型

1.2.1 自然对流传热

发动机在自然对流条件下降温,其对流换热系数可通过式(3)求解:

(3)

式中Gr为格拉晓夫(Grashof)数;g为重力加速度,m/s2;aV为空气的体胀系数;ΔT为发动机外壁与环境的温差,℃;D为发动机外径,m;V为定性温度(壁温和环境温度均值)下空气的热边界层相对厚度,m2/s;Nu为努塞尔(Nusselt)数;C、n为常数;Pr为定性温度下空气的普朗特数;h为壳体表面的对流换热系数,W/(m2·K);λ为定性温度下空气的热导率,W/(m·K)。

1.2.2 流体横掠单管强制对流

降温过程中若采用空调等强制降温措施,则可视为流体横掠单管强制对流,其对流换热系数可通过式(4)求解:

(4)

式中Re为雷诺数;u为空气流速;其余参数与式(3)定义一致。

2 有限元模型及分析方法

2.1 有限元模型

以某碳纤维壳体发动机药柱为研究对象,总长4690 mm,药柱最大肉厚300 mm,考虑发动机推进剂药柱、绝热层、人脱层、碳纤维壳体等主要部件。根据该发动机头尾翼柱形药柱结构特点创建了1/9结构三维有限元模型,共划分91 383个六面体单元,135 031个结点。在模型内取A(壳体表面)、B(药柱圆管表面)做输出分析,如图1所示。

图1 某碳纤维壳体发动机药柱有限元模型Fig.1 Finite element model of a carbon fiber case SRM grain

2.2 边界条件与计算工况

位移边界条件:对前连接头端面进行轴向固定,并在模型两侧对称面上施加环向对称约束。

热边界条件:假设发动机药柱零应力温度为68 ℃(固化温度60 ℃),降温过程只有壳体外壁散热,计算过程考虑热对流和热辐射边界条件(壳体表面辐射发射率为0.7),其余为绝热过程。

计算时,空气流速取固化间空调送风速度 1.5 m/s,结合固化降温工艺现实情况共考虑了以下6种载荷历程(总降温时间均为216 h,工艺(1)～(2)的初始环境温度为60 ℃):

(1)环境温度以1 ℃/h降温至40 ℃,再自然对流降温冷却,自然环境温度Ts=15+5×sin(t/12)(t为降温时间,h)。

(2)环境温度以1 ℃/h降温至40 ℃,再启动空调强制对流降温,空气流速1.5 m/s,空气温度20 ℃。

(3)环境温度以1 ℃/h降温至40 ℃,再启动空调强制对流降温,空气流速1.5 m/s,空气温度10 ℃。

(4)直接自然对流降温,自然环境温度Ts=15+5×sin(t/12)。

(5)直接强制对流降温,空气流速1.5 m/s,空气温度20 ℃。

(6)直接强制对流降温,空气流速1.5 m/s,空气温度10 ℃。

2.3 相关材料性能参数

该推进剂药柱为HTPB推进剂,其松弛模量曲线的8阶Prony级数表达式[19]为

(5)

参考温度为293.15 K时,时温等效WLF方程为

(6)

碳纤维壳体的材料力学参数见表1。

固化降温过程中三元乙丙绝热层的应变属于小变形,采用Neo-Hooken超弹模型,应变能形式为

(7)

药柱各部件的其他材料性能参数见表2,其中金属件包含前、后裙和前、后连接头。

表1 某碳纤维壳体材料参数Table 1 Material parameters of a carbon fiber case

表2 模型材料参数Table 2 Material parameters of the model

3 数值计算及结果分析

3.1 对流换热系数的变化

从图2所示的6种工艺条件下对流换热系数随时间的变化结果可知,降温初期工艺(1)～(3)对流换热系数相等,之后由于环境温度的突变导致对流换热系数的陡增。在降温后期,药柱温度场基本达到平衡,相同环境温度的工艺,其对流换热系数也趋于一致。自然对流条件下的工艺(1)和(4),受壳体表面温度下降和环境温度波动的耦合影响,对流换热系数出现正弦波动下降,且波动振幅有扩大趋势,最终在1～2.5 W/(m2·K)范围内波动。强制对流条件下的工艺(2)、(3)、(5)和(6),空气流速和空气温度为恒定值,对流换热系数只受空气物性参数的影响而波动较小,降温后期工艺(2)和(5)的对流换热系数稳定在7 W/(m2·K)左右,工艺(3)和(6)则稳定在7.3 W/(m2·K)左右。

图2 6种工艺条件下对流换热系数的变化Fig.2 Variation of convective heat transfer coefficient during six processes

3.2 温度场分析

由于该药柱肉厚较大、碳纤维壳体的导热系数较低,同时在降温后期与环境换热非常缓慢,导致降温结束后药柱内部仍存在不均匀温度场,从图3可以看出药柱温度场的梯度分布规律,温度最高点在药柱圆管中段区域,温度最低点在头尾部壳体表面。

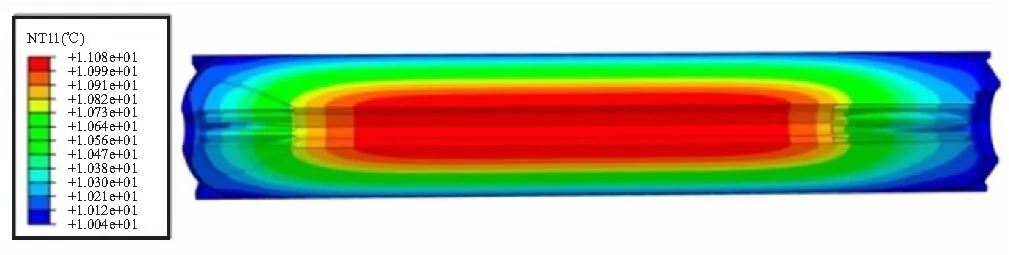
图3 工艺(3)降温后的药柱内部温度场Fig.3 Internal thermal field of grain after cooling process(3)

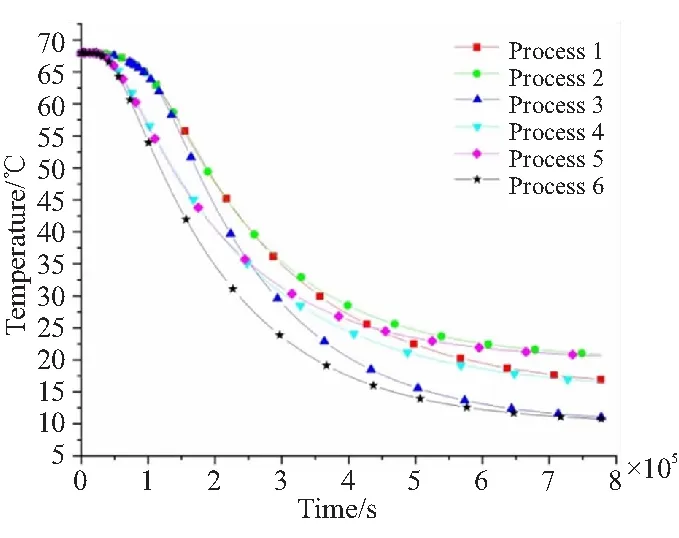
从图4(a)壳体表面(A点)温度曲线可以看出,工艺(1)～(3)在降温初期下降缓慢,之后由于环境温度的突变而出现降温拐点,开始迅速下降。工艺(1)和(4)壳体表面温度在降温后期呈现波动下降形态,这是因为自然降温阶段环境温度存在波动,而药柱内部导热及其与外界换热过程一直处于非平衡态,当环境温度较高时,壳体表面散失的热量小于药柱内部传导给壳体的热量,此时壳体温度升高;反之则壳体温度降低。在降温后期随着壳体与环境温差越来越小,对流换热过程变得异常缓慢,温度曲线也变得平缓。从图4(b)可以看出,药柱温度的下降相对于壳体表面存在滞后,降温初期和后期,曲线均较为平缓,在降温中期换热效率较高,曲线变化较为剧烈。降温过程药柱内温度场始终处于非平衡态,壳体与药柱的温差也在动态变化,如图5所示。降温初期温差快速上升,工艺(6)温差最大达44.5 ℃,之后快速下降并趋于平缓。降温结束后,工艺(1)温差最大,达2.12 ℃;工艺(5)最小,为0.56 ℃。

(a) Point A

(b) Point B图4 A点和B点温度-时间曲线|Fig.4 Temperature-time curves of point A and point B

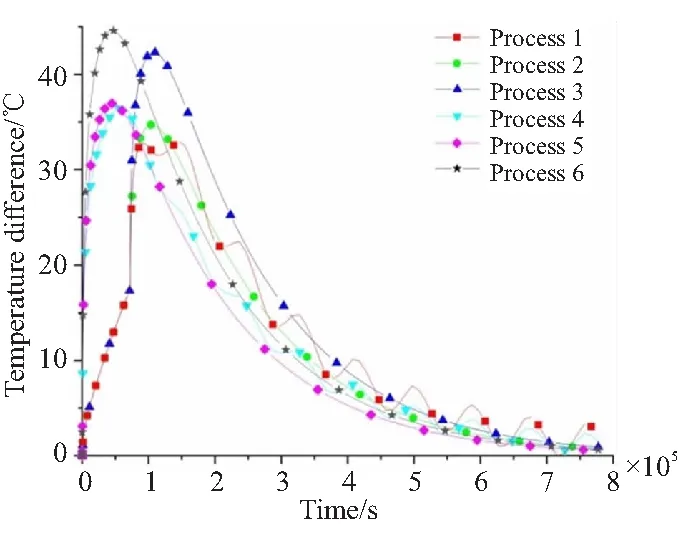
图5 温差-时间曲线Fig.5 Temperature difference-time curves

将与环境温差≤2 ℃视为温度平衡,工艺(1)、(4)的平衡温度定为22 ℃,则各工艺壳体和药柱的温度平衡时间见表3。可以看出,壳体温度达到平衡时,药柱温度尚未达到平衡,而药柱温度平衡时间相对于壳体温度平衡时间存在时滞,工艺(1)、(4)的时滞在(69±0.5) h范围内,工艺(2)、(3)、(5)、(6)的时滞则在(89±1.5) h范围内,这是因为温度平衡时滞主要与药柱肉厚和环境温度有关,不同肉厚的药柱可通过仿真计算得出其在不同环境温度下的温度平衡时滞。而对于该药柱,工程上难以监测降温过程药柱内部温度变化时,可通过监测壳体表面温度,结合温差变化规律和药柱温度平衡时滞估算药柱内的温度及其平衡时间。

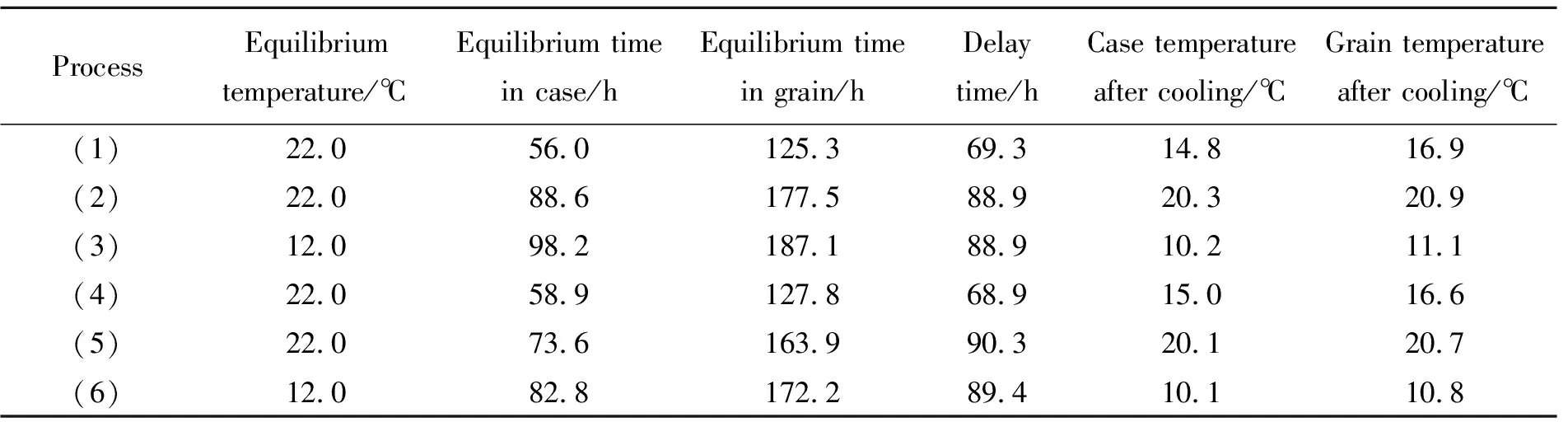
表3 壳体和药柱温度平衡时间Table 3 Temperature equilibrium time of the case and grain

3.3 结构完整性分析

3.3.1 应力-应变位移分析

降温后6种工艺的最大应力点均在后裙上,且金属部件应力显著高于非金属部件,如图6,药柱的应力应变和位移场如图7。药柱最大应力、应变和位移点均出现在圆管表面。头尾翼片处由于翼槽较宽,同时靠近人脱层,应力得以释放,导致应力较小。

图6 工艺(3)降温后药柱内部应力分布Fig.6 Internal stress distribution of grain after cooling process(3)

(a)Stress (b)Strain

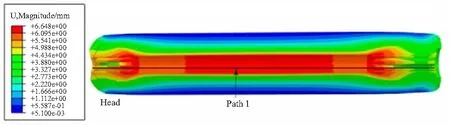
(c)Displacement图7 工艺(3)降温后药柱内部应力、应变和位移Fig.7 Internal stress, strain and displacement of grain after cooling process(3)

药柱位移场集中在圆管表面,工艺(3)降温后药柱圆管表面的实际位移通过π尺测量得到,测量时以头部端面为起始位置,沿图7(c)中路径1分别距起始位置200、600、1000、2500、3000、3700、4000 mm测量圆管表面位移实测值,并与仿真计算值的对比见图8所示。

由图8可见,位移实测在降温结束后一段时间进行,药柱内温度仍缓慢下降,由于推进剂的粘弹性松弛特性,药柱继续收缩导致实测值比计算值稍高,但整体位移分布规律可以较好吻合。计算值和实测值在距头部约600 mm和3700 mm的位置都有一个位移突变,这两处对应的是前、后翼片与圆管交汇处,药型的突变改变了位移场的分布。计算位移与实测值较好吻合说明考虑对流换热系数的动态耦合变化,能精确模拟药柱热载荷下的结构响应。

图9所示的是药柱圆管表面B点的应力-应变增长曲线。可以看出,工艺(1)～(3)由于降温初期降温速率较低使药柱应力-应变增长较为缓慢;工艺(4)～(6)在降温初期药柱与壳体温差最大使药柱应力-应变增长速率最大,之后随着温差减小而趋缓。在降温后期,药柱内部温度达到平衡,相同环境温度下的工艺(1)和(4)、(2)和(5)、(3)和(6)应力-应变趋于一致。从图5和图9可以看出,药柱应力-应变的增长速率与壳体-药柱的温差显著相关,因此调整工艺参数使降温过程壳体-药柱的温差尽可能降低,可以减小药柱的应力-应变增长速率,而降温结束后的药柱应力-应变水平与环境温度有关。

图8 工艺(3)降温后路径1的理论和实测位移Fig.8 Theoretical and measured displacement values of path 1 after cooling process(3)

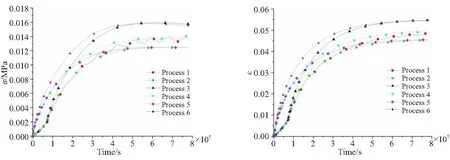
(a)Stress (b)Strain图9 B点的应力和应变增长曲线Fig.9 Growth curves of stress and strain at point B

3.3.2 结构完整性评估

复合推进剂药柱结构失效的破坏条件和破坏形式跟药柱承受的应力状态、加载历史、加载的应变率等很多因素密切相关。本文采用相应应变率下推进剂的最大伸长率作为药柱失效判据,为表征该药柱推进剂极限慢拉条件下的力学性能,采用哑铃型试件在低温条件下进行极限拉伸试验(0.1 mm/min,-10 ℃),得到该推进剂的最大延伸率εm为53.5%,最大抗拉强度为0.6 MPa。

药柱采用最大伸长率失效判据,其他部件采用等效Von-Mise应力准则进行结构完整性评估,结果见表4,经计算各部件均能满足结构完整性要求。

表4 安全系数计算结果Table 4 Calculate results of safety factors

其中,工艺(2)和(5)的药柱安全系数达到了 11.6,比安全系数最低的工艺(3)和(6)提高了 20.8%,说明固化降温工艺对药柱的安全系数有显著影响,调整降温工艺参数可以提高药柱的安全系数。

3.3.3 累积损伤分析

固化降温引起的热应力小于药柱的最大抗拉强度,不会使药柱直接失效,但药柱长期处于热应力下会造成累积损伤,导致推进剂性能下降,影响药柱的结构完整性[7]。

李尧[20]提出的简易累积损伤模型(式(8))可以有效反映推进剂的损伤破坏过程,并通过试验拟合出损伤参数。

(8)

通过累积损伤模型,将仿真计算得到的不同时刻药柱应变率及应力值代入公式,计算得到不同工艺下的药柱累积损伤曲线如图10所示。可以看出,工艺(6)条件下药柱的累积损伤最大,达到2.53%,工艺(2)累积损伤最小,为1.72%。工艺(1)～(3)相对于相同环境温度的工艺(4)～(6)的累积损伤水平要低8.1%～14.6%,是由于工艺(1)～(3)初期降温缓慢,减缓了药柱的应力和应变的增长速率,降低了累积损伤水平。因此,固化降温过程初期缓慢降温可降低药柱的累积损伤水平