爆破影响下测压钻孔密封起始位置的确定*

2023-11-14聂尧,张恒

陕西煤炭 2023年6期

聂尧,张恒

(1.中国煤矿机械装备有限责任公司,北京 100011;2.中国矿业大学(北京),北京 100083)

0 引言

煤层瓦斯压力是判别煤层是否达到抽放标准的重要依据,也是鉴定煤层突出危险性的重要指标。封孔是煤层瓦斯压力测定的基础,钻孔施工完需要先密封再进行压力观测。注浆和“胶囊-粘液”是井下常用的2种测压钻孔密封方式[1]。封孔过程中,需要考虑掘进巷道围岩松动圈的范围。如图1所示,巷道围岩松动圈范围内裂隙发育较为丰富,若钻孔密封段位于该区域范围内(图中L),可能导致封孔失效,进而导致测压失败。近些年来,为了解决钻孔密封可靠性,学者们基于巷道围岩松动圈理论对封孔起始位置和封孔深度进行了一些研究。YAO等[2]为了确定围岩破裂带从而提高钻孔封堵效果,通过理论分析、数值模拟等方式提出了一种基于恒压注气的方法用于确定钻孔密封深度,并进行了现场试验验证。ZHANG等[3]通过理论分析、数值模拟等方法提出了一种基于钻孔应力实时监测的封孔深度确定方法,研究表明合理的密封深度应比应力集中区大,并且确定了海子煤矿III1011工作面的钻孔密封深度。武炜[4]认为采掘巷道围岩塑性区内岩石破坏严重,封孔时应该避开围岩松动圈范围,并通过理论推导和数值计算得到了巷道围岩塑性区半径,确定了钻孔密封起始位置。而对于围岩松动圈范围的求解,王睿、陈秋南等[5-6]基于Hoek-Brown强度准则推导了围岩松动圈厚度计算式,并进行了算例分析。刘永胜、陈亚楠等[7-8]基于现场测试和数值计算对爆破作用下围岩松动圈范围的影响进行了分析探讨。

1-压力表;2-加压手轮;3-胶圈;4-测压管;5-胶圈(胶囊);6-三通;7-注气罐;8-粘液压力;9-粘液罐;10-粘液;11-孔口; r-巷道半径;R-围岩松动圈半径;L-巷道测压钻孔孔口距胶圈(胶囊)距离

但是,巷道爆破掘进过程中,爆破扰动和原岩应力会共同影响巷道围岩松动圈的范围。因此,首先分析巷道围岩松动圈的应力状态,通过理论推导获得了原岩应力作用下围岩松动圈半径计算式。接着,结合爆破力学得到了爆破冲击和原岩应力共同作用下的巷道围岩松动圈半径解析式,并进行现场算例分析。

1 围岩松动圈范围计算模型

1.1 损伤变量

根据双直线模型[9],岩石破坏过程中的损伤分为弹性阶段和应变软化阶段,假设损伤为各向同性的,因此

(1)

式中,σc,εc为峰值点位的应力、应变;σu为岩石残余应力;εu为岩体稳定应变。

根据力的等效原理[10]

σ=(1-S)εE

(2)

式中,S为损伤变量;E为岩石弹性模量。设定参数Dv,定义其为岩石损伤模量为

(3)

1.2 无损伤时的应力解

经典的M-C准则见式(4)[11]

(4)

式中,σθ,σr分别为围岩切向应力和径向应力,MPa;c为内聚力;φ为岩石的内摩擦角,(°)。

平衡方程见式(5)

(5)

几何方程为

(6)

物理方程为

(7)

式中,γrθ为切应力;τrθ为剪应力。

边界条件为

σr=R0=0

(8)

(9)

根据摩尔库伦准则、平衡方程和上述边界条件可以求解出损伤区域内应力分量为

(10)

式中,R0为巷道半径;r为巷道围岩任一点半径;L为松动圈半径。

根据平衡方程、物理方程和几何方程得到弹性区内的应力分量为

(11)

(12)

式中,σ0为原岩应力;LP为损伤区半径。

1.3 出现损伤时的应力解

客观上,损伤变量S未达到1时,材料就已经发生破坏[10]。材料破坏准则式(4)可以修正见式(13)

(13)

联立式(10)～式(12),根据应力连续性条件,得到损伤区应力分量见式(14)

(14)

岩体出现损伤时,在岩体任意一点r=Lp,可以得到式(15)[12]

L=LP(S+E/(Dv+E))1/2

(15)

因此,巷道围岩松动圈(损伤破坏区)半径的表达式为

(16)

因此,巷道围岩松动圈厚度见式(17)

RL=Lp-R0

(17)

式中,RL为松动圈厚度。

2 爆破影响下围岩松动圈范围计算

爆破是井下岩巷掘进过程中岩石破碎的主要方式。以往围岩松动圈范围的确定和求解仅考虑了原岩应力作用的影响,但炸药爆破产生的冲击波以及衍生的岩石应力波会在一定程度上导致松动圈范围内裂隙进一步扩展[13]。对于多数岩巷,炸药爆破后冲击波和应力波会使炮孔围岩损伤加剧,因此爆破产生的松动圈裂纹扩展不能被忽略。

2.1 爆轰波理论

耦合装药条件下,柱状药包爆炸瞬间产生的爆轰波向岩体施加强冲击载荷,根据声学近似理论[14]

(18)

(19)

(20)

式中,p0,p1分别为冲击波冲击前后的压力;Ds为爆轰波速;ρ1,ρ2分别为炸药爆炸产生冲击波前后的炸药密度;ks为爆轰气体等熵膨胀系数,一般取3。Cp为岩石内弹性纵波波速;设岩石初始参数为pm=p0,ρm在初始阶段均为0。

炸药起爆后,高压爆轰波瞬时作用在炮孔内壁面,爆破冲击波不断衰减为应力波在岩石中传播。而定义Z为冲击波载荷传播衰减系数,其反映了冲击波传递过程载荷的衰减程度,多数学者认为Z可用式(21)表征[14]

(21)

式中,μd为岩石动态泊松比。

岩石泊松比与岩石的应变率呈负相关性,但也有文献通过实验发现岩石泊松比与应变率关系较为离散。文献表明,工程中一般可以用式(22)来表征岩石动静泊松比关系[15]

μd=0.8μ

(22)

式中,μ为岩石的泊松比。

定义I为侧向应力系数为

(23)

2.2 爆炸影响下的岩石破坏准则

材料物性参数和外加载荷大小决定了其破坏程度。可认为岩石是脆性材料,其抗拉强度远小于其抗压强度。根据Mises屈服准则,空间视角下若材料中任一点强度σi满足式(24),材料内部将发生屈服,进而导致破坏

σi≥σtd

(24)

式中,σtd为岩石单轴动态抗拉强度。

根据相关研究,岩石动态抗拉强度与岩石加载应变率变化之间的关系并不明显。因此,对于工程爆破,在岩石加载应变率范围内,可取[16]

σtd=σt

(25)

式中,σt为岩石单轴静态抗拉强度。

此外,在爆破钻孔打钻成孔后,爆破孔周边岩石会有损伤。按照断裂力学观点,炮孔成孔后附近岩石初始损伤会在一定程度上影响炸药冲击波作用和应力波能量传递效果[17]。但是,初始损伤导致的裂纹是爆破冲击裂纹扩展的重要基础。然而,多数研究并未考虑初始爆破孔围岩损伤情况。因此,考虑引入损伤因子J来表征岩体初始损伤,因此式(25)可以修正为

σtd=(1-J)σt

(26)

式中,J为损伤因子,一般取值0.4～0.6[18]。

基于上述讨论,炸药爆破冲击波强度大于岩石临界强度时,炮孔围岩将发生破坏。而爆炸冲击波在岩体中快速衰减为岩石应力波,且当作用于松动圈时,在其裂纹尖端处会发生应力集中,使得应力波载荷产生巨大破坏力,使得松动圈范围内裂纹进一步发生扩展和破坏。因此,围岩松动圈范围的确定受到原岩应力和爆破共同影响。

炸药爆破过程中,爆破动载对炮孔围岩的作用如图2所示。柱状装药常用于煤矿爆破掘进,炸药起爆瞬间产生的冲击波以一定角度入射到围岩壁面,而炮孔内壁面的裂纹处于相对复杂的应力状态。岩石的断裂模式(裂纹扩展方式)有张开型、撕裂型以及滑移型3种,张开型是岩体爆破主要的裂纹扩展方式[17]。为了简化材料应力分析,这里只选取张开型裂纹扩展模式对岩石断裂的影响。

1-柱面波;2-柱状装药;3-爆破应力波入射方向;4-松动圈

岩石爆破面爆轰波衍生的应力波大于另一侧,而顶部受到的冲击影响要大于底部,采矿工程中主要表现为顶板垮落和片帮。以巷道顶部爆破为例对松动圈裂纹扩展进行力学分析,具体如图3所示。

σin-炸药爆破入射应力;σind-垂直于巷道侧壁的应力垂直分量;α-σin和σind的夹角;L1-炮孔药卷中心至巷道中心水平距离;L2-炮孔药卷中心至巷道顶部垂直距离

炸药爆炸瞬间岩石应力波可以视为柱面波,应力波强度衰减程度与传播距离正相关。因此,应力波初始入射应力见式(27)

(27)

式中,p2为炸药爆轰波压力;r0为炮眼半径。

炸药爆炸瞬间,爆轰波载荷入射在岩石壁面,在爆破应力波遇到自由面时发生反射,压缩应力波则变化为拉伸波,进而引起径向裂隙延伸扩展。因此入射应力垂直方向分量是张开型裂纹扩展主要原因,可以表示为

σind=σin×cosα

(28)

(29)

(30)

入射应力在垂直方向上分量σind的衍生拉应力σind2见式(31)

σind2=I×σind

(31)

因此,由于σind2的作用,最终造成巷道围岩松动圈内裂纹进一步扩展。爆破应力波远区作用裂纹的最大扩展长度可表示为[19]

(32)

爆破影响下围岩松动圈扩展长度可表示为

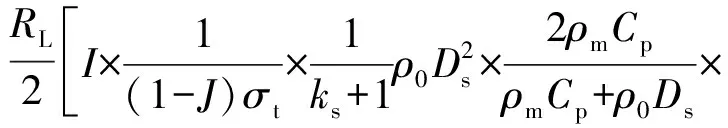
(33)

因此,围岩松动圈半径和厚度计算式可以表示为

RR=Lp+rmax

(34)

Rr=RL+rmax

(35)

式中,RR,Rr分别为爆破和原岩应力协同作用下松动圈半径和厚度;RL为原岩应力影响下的松动圈厚度。

炸药爆破过程中,爆破冲击波衍生的岩石应力波会作用于围岩松动圈,当其拉应力大于岩石抗拉强度时,已有的裂隙就会出现进一步扩展、贯穿,而爆生气体则会加剧裂纹的扩展。

3 测压钻孔封孔起始位置确定

前述给出了巷道围岩松动圈范围计算式,本节采用相关文献数据进行算例验证。算例唐口矿相关工程地质参数[20]为:巷道半径为3.0 m,原岩应力σ0为23.77 MPa,内摩擦角φ为30°,泊松比为0.25,内聚力为1.5 MPa,取E/Dv=1。我国井下爆破打孔多用φ35 mm到φ50 mm的钻头[21],本节模型计算时选择φ50 mm作为炮孔直径参数。此外,煤矿常用安全炸药的参数[22]见表1,炸药爆速取值3 500 m/s,炸药密度取1 000 kg/m3,岩石中纵波波速取3 400 m/s。

表1 常见矿用安全炸药参数[22]

按照上述初始参数设定,基于Matlab计算得到原岩应力和爆破共同影响下的围岩松动圈半径,将不同文献模型和文中模型计算结果对比,见表2。不同模型计算结果及误差如图4所示。

表2 基于不同模型的松动圈范围计算结果

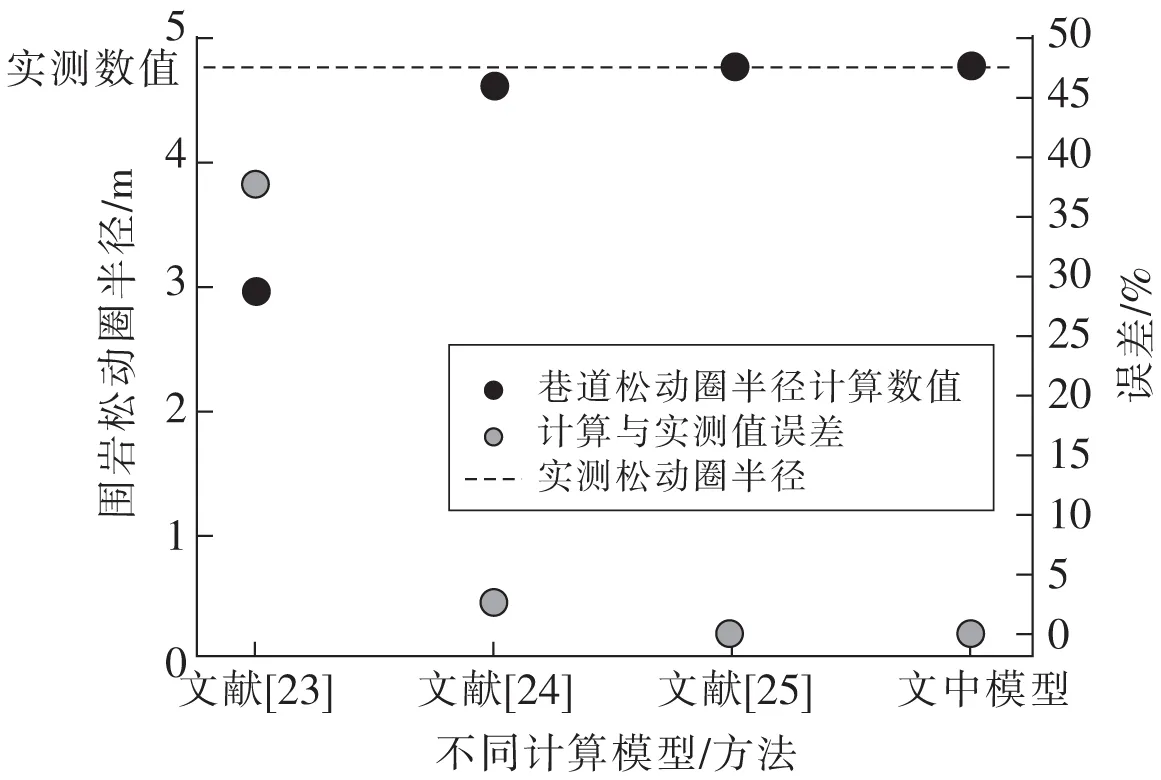
图4 不同模型计算结果及误差

可以看出,文献[23]计算结果与实测数据相差较大(37.7%),文中模型和文献[24,25]对松动圈半径的计算结果与实测数据误差0.6%、0.2%,结果误差较小,说明文中构建的模型可以很好地描述掘进巷道围岩松动圈的范围。此外,根据上述计算结果,计算得到了给定现场工程条件下巷道围岩松动圈半径和厚度分别为4.77 m和1.8 m。但是,对封孔起始位置的确定,不能单纯以大于松动圈厚度为判定标准。空间视角下,要结合测压钻孔方位角和倾角来综合确定。图5为钻孔封孔起始位置距孔口的长度示意图。可以看出,要使封孔段位于松动圈范围以外,就需要孔口至钻孔密封起始位置的长度(图中Ls)在巷道断面上的投影距不小于松动圈厚度(图中Rr)。因此,算例中孔口至钻孔密封起始位置的距离在巷道断面上的投影距应不小于1.8 m。而针对不同现场条件,可据实改变文中模型相关参数从而计算确定相应现场条件下钻孔密封起始位置。