计及相位角度关系的抽油机曲柄轴转矩自适应控制

钱国明

(中石油煤层气有限责任公司韩城采气管理区,陕西 韩城 715400)

如果煤层中含有大量的煤层水,使煤层储存量超出解吸量,在天然气开采时就需要将煤层水排出,使其储层压力降至解吸压力之下,进而完成煤层气解吸附[1-2]。排水层最常用的机械设备是抽油机,其具有内部构造简单、易于制造、可靠性高及维修成本低等优点,在煤层气开采机械设备中占有重要地位[3]。

抽油机简单的结构特征使各部件之间力传动影响较大,导致其具有曲柄轴转矩波动幅度大、能量损失严重以及悬点荷载量大等缺点[4]。其中转矩波动误差与悬点荷载是影响抽油机耗能及其效率的主要因素。转矩误差大不仅会增加抽油机输出功率,同时还会使电机大部分作业处于低速运行阶段,降低抽油机作业效率;而悬点荷载量大会使偏心栏杆处于非平稳运行状态,影响抽油机系统的稳定性,进而使电机做负功,增加能耗,且会使设备处于恶劣的工作状况中。此外,冲击荷载还会对抽油机内部零件造成不同程度损伤,缩短抽油机使用寿命。

基于此,诸多学者对降低抽油机能耗与提高作业效率进行了深入研究。胡其杰等[5]在分析抽油机内部结构的基础上,设计了曲柄轴转矩控制系统,通过MATLAB得出转矩控制参数,完成曲柄轴转矩控制。该方法能够有效抑制曲柄轴转矩波动,但未考虑悬点荷载过大问题,会损失部分能量。李雪等[6]在分析抽油机曲柄运动受力情况后,使用Java Web设计抽油机控制系统,实现曲柄转矩与偏心连杆平衡调节。此方法虽然在曲柄轴转矩控制方面取得了一定效果,但控制功耗较大,实用性较差。

抽油机作业过程中,若曲柄轴转矩波动过大,抽油机运行能耗将增加,这是因为上述文献中的传统控制方法无法结合波动情况自适应调整参数。为了进一步提升抽油机控制效果,降低能耗,本文提出一种计及相位角度关系的抽油机曲柄轴转矩自适应控制方法。

1 曲柄轴相位角度关系分析

偏心连杆平衡抽油机主要由3个部分构成,即曲柄、连杆和游梁臂[7-8]。游梁臂前端通常会安装一个圆弧形零件(即炉头),其表面上的悬点借助钢丝绳完成抽油杆安装,同时还能将圆弧运动转化成抽油机的直线往复运动。曲柄上安装了一个平衡块,使电机驱动曲柄旋转时,抽油杆能够上下运动,从而带动抽油机作业,图1所示为抽油机作业简图。

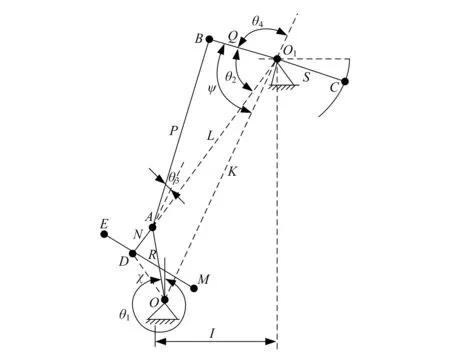
图1 抽油机作业简图

图1中,P为连杆AB的长度;Q、S为游梁前、后臂长度;K为OO1的长度,即偏心距;I为OO1的水平投影;L为AO1的长度;N为偏心连杆AD的长度;χ为OD长度,C为悬点;R为EM之间的曲柄长度。各杆参考角分别为θ1、θ2、θ3,则P与Q的运动角速度求解公式为:

(1)

式中:Vθ3为杆P与Q参考角θ3的运动角速度,Vθ4为杆P与Q参考角θ4的运动角速度。

假设EM匀速旋转,则悬点C速度VC计算公式为:

VC=S×(Vθ3-Vθ4)

(2)

假设悬点处于极限位置(上、下死点)时,Q、K之间夹角ψ的两个极值分别为ψmin和ψmax,求解公式为:

(3)

假设垂直向上方向为正,下死点位置为(0,0),则悬点C的位移SC求解公式为[9]:

(4)

联立公式(3)和公式(4)获得SC的位移最大值Smax计算公式为:

(5)

假设偏心连杆失衡,平衡块重心安装位置从A点转移到M点,则驱动电机的安装位置也会随之改变,即从O移到O1,此时需要分析出θ1、θ2之间的关系,则有:

(6)

由此通过运动学分析获得悬点位移最大值和偏心连杆失衡下曲柄轴相位角度关系,根据分析结果即可进行曲柄轴转矩控制。

2 曲柄轴转矩自适应控制

由于偏心连杆平衡抽油机曲柄轴转矩控制过程较为复杂,根据第1章分析出的悬点位移最大值和偏心连杆失衡下曲柄轴相位角度关系,对曲柄轴转矩控制进行优化,从而抑制曲柄轴转矩波动,实现偏心连杆自适应平衡,提升抽油机机身工作效率,节省大量电力能源[10]。

2.1 控制目标函数构建

悬点荷载的周期性变化特征与曲柄轴的运动特性,会使偏心连杆受力不均,无法达到平衡状态,严重影响抽油机内部零件的使用寿命及整机能耗。悬点荷载与悬点加速度有关,加速度越小,其惯性荷载越小,偏心连杆稳定性越强,抽油机作业效率越高。曲柄轴的波动幅值是影响零件寿命的关键因素之一。若曲柄轴转矩能得到有效控制,即其均方根转矩值越小,则抽油机输出功率越小,抽油机系统能耗越小。为此,将悬点荷载、曲柄轴转矩均方根最小作为优化目标,建立目标函数。

1)悬点荷载最小化。

悬点位移最大时,悬点加速度a求解公式为:

a=v×Smax

(7)

v=VCWl+Wdsin(θ4-θ2)-v1Q1sinψ-MAsin(θ1-τ)

(8)

式中:v为游梁的角线速度,Wl为游梁结构荷载的等效不平衡量,Wd为偏心连杆质量与自身质量的等效平衡荷载,v1、Q1分别为游梁平衡时的荷载及其线速度,MA为平衡转矩极限值,τ为曲柄平衡时的相位角。

悬点荷载目标函数求解过程为:

(9)

式中:W为悬点荷载量,u为平衡重心x处的位置,El为杆的弹性模量,H为下泵深度,ρR与ρ分别为杆与天然气的密度。

根据式(9)可知,减小悬点加速度a,可降低作用于偏心连杆的荷载。在相同荷载情况下,降低悬点荷载,即降低偏心连杆的负载,就能避免杆柱出现断脱的情况,提升连杆使用寿命。

2)曲柄轴转矩均方根最小化。

曲柄轴转矩与抽油机能耗有关,曲柄轴转矩的均方根Me越小,抽油机输出功率P1越小,目标函数求解公式为:

(10)

式中:ω为曲柄轴转矩能耗在抽油机总能耗中的权重,η为抽油机的工作效率。

(11)

式中:Mn为n个曲柄轴的净转矩,其受到悬点荷载的影响;n为曲柄轴数量。Mn求解过程为:

(12)

通过式(10)～(12)可得:在悬点荷载下,降低Me值,能降低抽油机电动机的输出功率,使曲柄轴转矩的波动最小,在保证工作效率的同时达到装机功率最小的目的,进而实现节能。另外,转矩波动越小,悬点转动荷载也会随之变小,从而能够有效延长抽油机内部各部件的使用寿命。

2.2 曲柄轴转矩自适应控制变量约束条件设定

为使抽油机达到最佳工作效率,能耗最小,还需要对曲柄轴转矩与偏心连杆保持平衡的相关变化量进行约束。

曲柄轴转矩与偏心连杆保持平衡的相关变化量有:

1)平衡重心位置u。

一次平衡由一次曲柄与一次平衡块构成,一次平衡块质量已知,可通过调整此平衡块重心在曲柄上位置来改变一次平衡重心位置u,以达到平衡偏心连杆的目的。因为平衡块位置变化对一次平衡中的τ影响极小,所以可不考虑二次平衡位置变化对τ的影响,也可将一次平衡位置与τ分别看成独立变量,将τ看作一个固定值。

2)平衡质量Wd。

偏心连杆质量与自身质量等效平衡荷载(即平衡质量)Wd对一次平衡都有很大影响,即Wd也是曲柄轴控制变量。

3)平衡偏置角τ1。

二次偏心连杆平衡偏置角即两次平衡叠加的相位角,τ1的变化量直接决定τ的大小,同时τ的变化也会影响二次平衡作用在曲柄轴的转矩波动幅度。

曲柄轴转矩与偏心连杆平衡控制参数可表示为:

X=[u,Wd,τ1]T

(13)

式中:X为曲柄轴转矩与偏心连杆平衡控制参数矩阵。

为了使抽油机的偏心连杆平衡效果和曲柄轴转矩控制效果最佳,对u、Wd、τ1变量制定约束条件,即:

0≤u≤R

(14)

0≤Wd≤5 000 kg

(15)

0≤τ1≤2π

(16)

式中5 000 kg为二次曲柄及其平衡块质量总和。将式(14)～(16)作为目标函数约束条件,为控制参数设定限制范围,将约束参数代入到目标函数式(9)和式(10)中,完成曲柄轴转矩自适应控制。

3 实验过程与结果分析

3.1 实验参数

实验选用的抽油机型号为CYJ10-3-53HB,内部结构参数见表1。由上述分析可知,悬点荷载是曲柄轴转矩控制的关键影响因素,因此为了验证本文所提方法(简称本文方法)的抽油机控制效果,实验方案为向悬点施加一定的荷载,如图2所示。

表1 抽油机内部结构参数 单位:mm

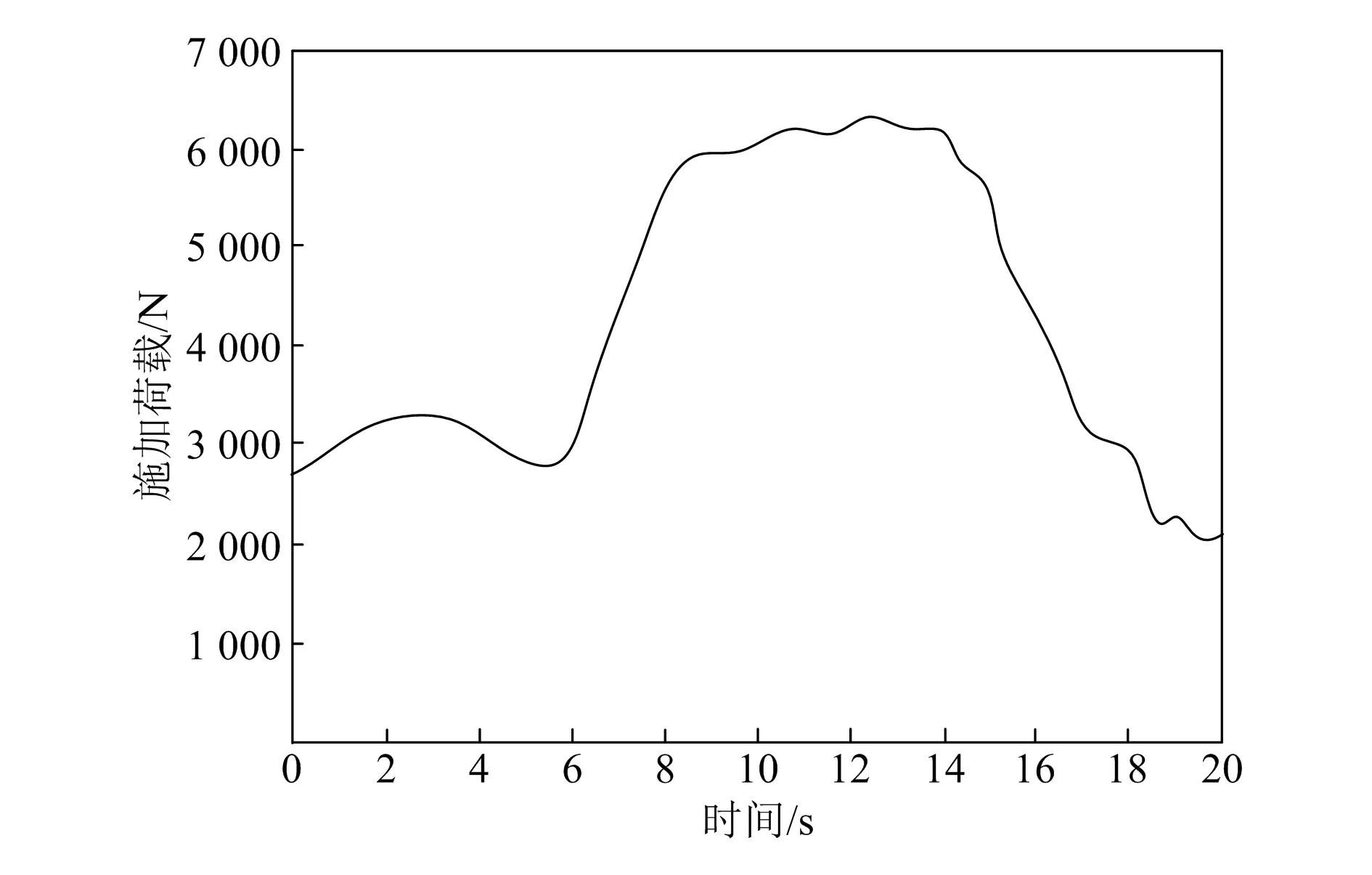
图2 悬点荷载变化情况

将Hottinger Baldwin Messtechnik负载传感器安装在抽油机的悬点位置上,测量悬点处的重力或压力,并将其转换为电信号,输入到仿真平台。通过控制系统,采用动态加载方式,施加荷载到抽油机的悬点位置,初始荷载为2 800 N,加载次数为20次。将National连接到仿真实验平台的传感器上,实时获取传感器测得的数据,并将其记录下来。使用MATLAB仿真平台对数据进行分析处理,通过Tableau将数据以图表、图形等形式展示出来。

3.2 实验过程分析

设定抽油机运行1周时间为20 s,以保证实验结果有效性。测试在悬点荷载变化时,本文方法、SRM方法(文献[5])、Java Web方法(文献[6])对悬点运动分析和曲柄轴转矩控制的时间曲线,如图3～图4所示。

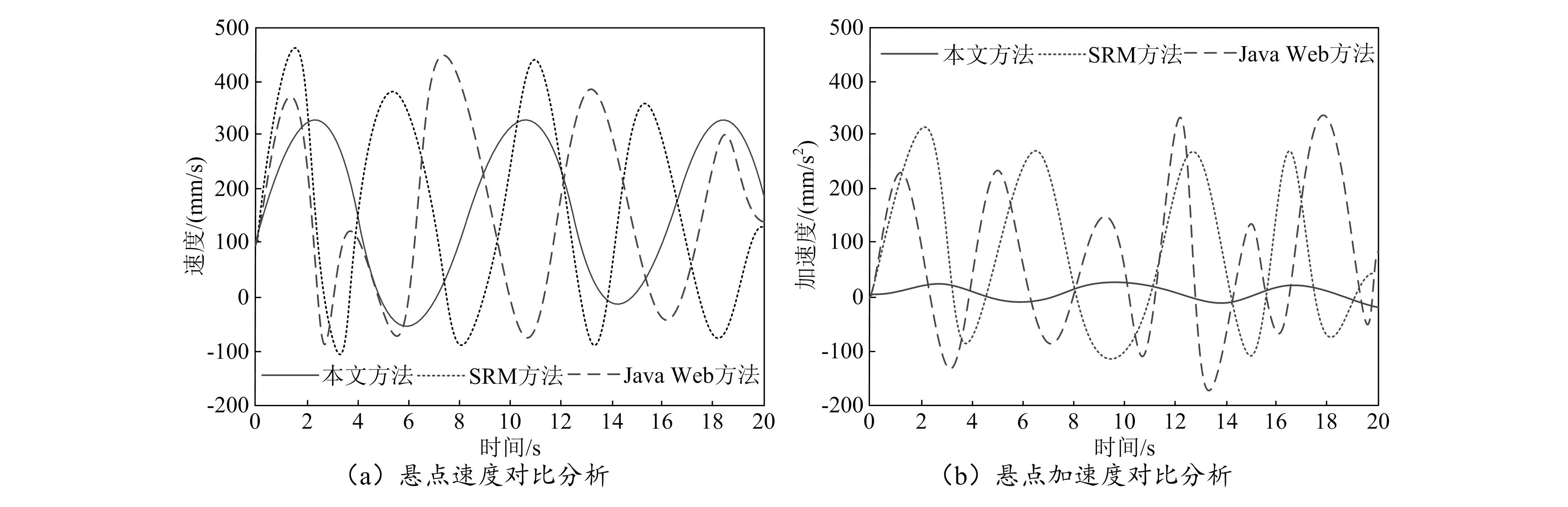
图3 悬点运动分析

3.2.1悬点运动分析

从图3(a)悬点速度变化曲线可知,本文方法对应的悬点运动速度曲线变化具有规律性,且曲线上下浮动极小,表明本文方法能够保证悬点匀速运动,使偏心连杆处于平衡状态,降低偏心连杆的负载,进而保证抽油机处于最佳作业状态;图3(b)中,本文方法的悬点加速度曲线波动最小,加速度越小,连杆荷载越小,因此抽油机作业较为稳定。而其他方法的悬点运动速度不太规律,容易导致偏心连杆的负载突然增加,杆柱出现断脱。

3.2.2曲柄轴转矩控制效果对比分析

为验证本文方法的曲柄轴转矩控制效果,对曲柄轴转矩旋转角速度、角加速度控制情况进行分析,结果如图4所示。

从图4明显看出,与其他方法相比,本文方法的曲柄轴转矩角加速度曲线波动最小,提升了偏心连杆平稳性,曲柄轴转矩控制效果最佳。这是因为本文方法能够找出最佳转矩控制参数,对曲柄轴的角速度、角加速度进行有效控制,角速度曲线变化具有规律性,表明本文方法能够保证曲柄轴匀速运动;SRM方法和Java Web方法都不能有效控制曲柄轴运动过程中的角加速度,导致曲柄无法进行匀速运动,曲柄轴转矩控制效果较差。

3.2.3抽油机能耗对比分析

抽油机能耗是检测曲柄轴转矩控制效果的关键指标之一,能耗值越小,表明抽油机能量损失越少。分别测试应用SRM方法、Java Web方法与本文方法时的抽油机能耗,结果如图5所示。

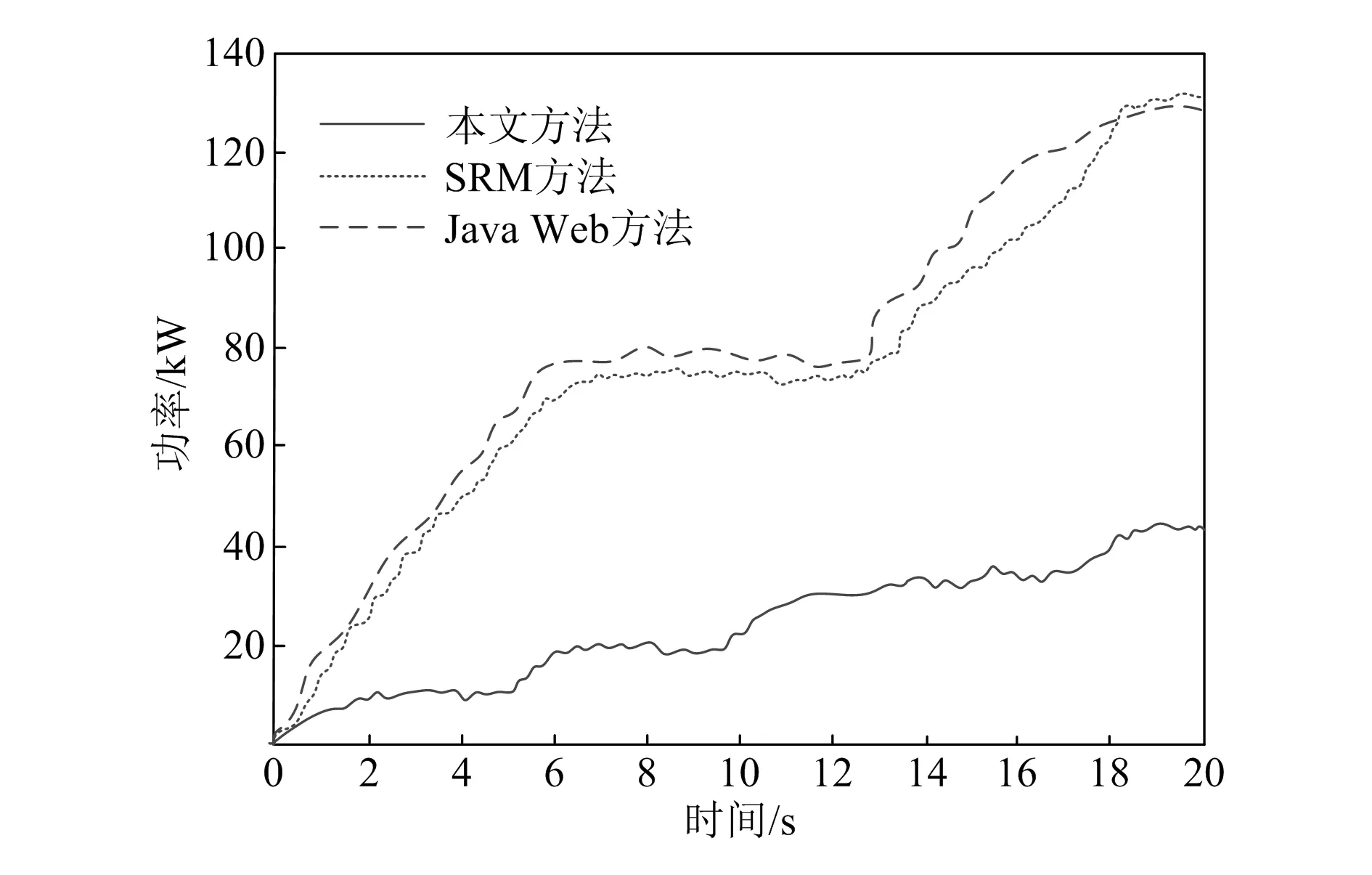
图5 3种方法的抽油机耗能对比分析

通过图5所示抽油机20 s内功耗曲线可知,随着时间增加,3种方法的抽油机能耗都在增加。但本文方法能够有效控制曲柄轴转矩,降低转矩波动幅度,提升效率,从而大幅度减少抽油机能耗,功率上升趋势远小于SRM方法、Java Web方法,低于50 kW。

4 结束语

为了解决抽油机曲柄轴转矩波动大、偏心连杆平衡效果差、装机输出功率能量损失严重等问题,本文设计了一种计及相位角度关系的抽油机曲柄轴转矩自适应控制策略。

为了使抽油机达到最佳作业效率,基于运动学原理分析抽油机作业原理,制定曲柄轴转矩控制参数的约束条件,找出最佳控制参数,进而使偏心连杆达到平衡运动状态。实验结果证实本文方法能够自适应调节曲柄转矩,并能保证其控制效果,进而使抽油机达到最佳作业状态,节省大量能源,可为提升煤层气开采抽油机机械设备的工作效率提供一种可行的技术方案。