逆向可变车道开口位置动态调整及信号配时优化方法研究
2023-11-13白家安张存保
白家安 张存保 曹 雨
(武汉理工大学智能交通系统研究中心 武汉 430063)
0 引 言
逆向可变车道在中央分隔带处设置固定开口及预信号等,使得车辆可借出口道进行左转,分时复用出口道空间资源,具备改造方便、投入小且效益高等优点,因此在国内被快速推广并取得了显著的效果[1-2].国内外学者对逆向可变车道信号控制优化进行了诸多研究.Zhao等[3]构建交通流量、主预信号控制及逆向可变车道长度等约束条件的混合整数线性规划模型进而优化信号配时.任其亮等[4]建立了以通行能力和延误为目标,考虑逆向可变车道长度及主预信号控制等约束的信号配时优化模型.刘伟[5]以各相位有效绿灯和逆向可变车道长度等参数为变量,以交叉口通行能力与延误为优化目标,利用NSGA-II算法进行求解.陈松等[6]分析左转车到达驶离的可能情况,构建各种情况下的左转车辆延误计算方法,最终以交叉口车均延误最小为目标对逆向可变车道信号配时进行优化.张泰文等[7]利用检测器获取车辆到达率、车道饱和流率与剩余排队车辆数等实时交通流数据,根据车流到达驶离图示推导交叉口车均延误计算公式,构建以延误最小为目标的交叉口信号配时动态优化模型.童蔚苹等[8]以泊松分布拟合车辆到达建立通行能力公式,以通行能力最大为目标利用迭代算法求解得出逆向可变车道长度与左转相位时长.
综上所述,现有研究大部分为固定逆向可变车道长度下的信号配时优化方法,而在实际运行中,由于逆向可变车道开口为人工或定时启闭等,常出现闲时借道空间浪费或高峰期借道空间不足的状态[9].实际上每周期的左转车辆数均对应着一个最佳逆向可变车道长度,而为了安全方面的考虑,车道长度改变不应太频繁,因此需要提出开口位置动态调整方法,确定不同时段的适宜逆向可变车道长度,依据开口状态及逆向可变车道长度优化信号配时.以武汉市古田四路长丰大道交叉口为例,与固定开口的定时控制及文献优化方法进行对比,利用VISSIM仿真验证优化方法的科学性与有效性.
1 逆向可变车道开口动态调整方案
1.1 逆向可变车道交叉口基本概述
逆向可变车道交叉口几何渠化设计模式见图1,在信号控制相位方案选择上,常见可分为三相位方案与四相位方案,见图2.

图1 逆向可变车道交叉口几何设计模式

图2 三、四相位信号控制相位相序
本文研究采用图2b)的四相位信号控制方案,以东西进口道均设置了逆向可变车道为例.第1相位和第2相位分别为南北左转和直行对称放行,在第2相位南北直行放行期间,预信号绿灯亮起,东西左转车辆提前进入逆向可变车道,第3相位东西左转相位放行,逆向可变车道车辆与常规左转车道车辆均可左转,为安全考虑,预信号在第3相位结束前提前结束,第4相位则放行东西直行车辆.
1.2 逆向可变车道开口动态调整方案
1.2.1基本假设
方案实现基于以下假设进行分析:①以常规十字信号交叉口为例,按图3要求设置逆向可变车道布局,包括中轴平移式前后开口护栏,视频检测器及主预信号灯等.前后开口护栏采用中轴平移式,具体设置形式见图4.1号视频检测器用于实时检测进口道车辆的排队车辆数、到达车辆数和驶离车辆数.2号视频检测器用于检测是否有左转车辆驶入开口,保障开口动态调整的安全性.②相位相序以图3四相位信号控制方式放行.③在逆向可变车道开口开启时开口宽度设定为固定值,保证左转车辆可正常转入逆向可变车道即可[10].

图3 逆向可变车道开口动态调整基础设置

图4 动态开口前后护栏设置形式(中轴平移式)
1.2.2开口动态调整及信号配时优化流程
本节基于假设提出了逆向可变车道开口动态调整流程见图5,基于检测器数据与历史流量数据短时预测未来时间段的左转直行交通量,依据预测交通状态量分析判别开口动态调整指标,以此决定是否进行动态调整,而后依据逆向可变车道开口状态对信号配时优化.

图5 逆向可变车道开口动态调整流程
1) 短时交通流预测 利用卡尔曼滤波对交叉口左转直行流向交通流量进行短时预测,设定逆向可变车道交叉口信号最大周期为120 s,预测时间间隔为5 min[12],最终得到预测间隔内各流向任意时刻的到达车辆数.
a(t)=q(t)/Δt
(1)
式中:q(t)为t时间段的流量预测值;a(t)为此预测间隔内任意时刻的到达车辆数.
2) 动态调整指标 ①调整稳定性 除每日首次逆向可变车道开口调整外,设置逆向可变车道开口调整的最小时间间隔Δt为10 min,控制间隔须超过Δt;②启闭效益判定 利用第2节信号配时优化方法分别获得逆向可变车道关闭和开启两种情况下,优化后的交叉口车均延误d0与d1.如开启后的逆向可变车道交叉口车均延误较关闭时更小,则说明逆向可变车道开启状态效益更佳,可考虑开启开口;③饱和度判定 当左转直行车流饱和度同时大于饱和度限值(一般取0.9)时才考虑开启逆向可变车道.以逆向可变车道开口初始状态为关闭为例,当xl>0.9且xs>0.9时,左转直行交通需求已达到开启逆向可变车道的要求,但还需进一步判定.当xl<0.9且xs<0.9时,逆向可变车道继续保持关闭,对信号配时方案优化.当xl>0.9且xs<0.9时,考虑设置可变车道或优化信号配时方案,以增加左转车流有效绿灯时间.当xl<0.9且xs>0.9时,逆向可变车道开口保持关闭,优化信号配时方案,缓解直行车流压力过大的情形.逆向可变车道初始状态为开启时,如后续时段左转直行饱和度均大于0.9,可考虑对开口位置进行调整,但是还需进一步分析调整稳定性,其他情形下则关闭开口,关闭时机通过调整稳定性进一步判定.
设定系数N记录达到动态调整要求的连续周期数.依据实地观测经验,直至N≥3时,才最终实施逆向可变车道开口动态调整.
3) 逆向可变车道长度 当逆向可变车道交叉口一个周期内左转车辆数等于常规左转车道与逆向可变车道排队车辆数总和时,交叉口通过量达到最高.而逆向可变车道长度决定着在逆向车道上排队车辆数总和,因此恰好将一个周期能够全部排空左转车辆的逆向可变左转车道长度视为适宜逆向可变车道长度.
由于动态开口调整间隔设定为10 min,动态调整间隔内逆向可变车道长度不再改变,开口控制间隔内周期时间相等,可视周期的适宜逆向可变车道长度即动态开口调整间隔的最佳逆向可变车道长度.
(2)
式中:Lcll为适宜的逆向可变车道长度,m;ql为预测周期左转车辆总数;Lpcu为平均车辆长度(含平均停车间距及车长),设定为6 m;Nl,ncll,nl分别为常规左转车道容量车数,逆向可变车道数与常规左转车道数.
依据实地调查及相关文献研究取逆向可变车道长度最小与最大值为15,150 m.因此,存在约束条件.
Lmin≤Lcll≤Lmax
(3)
式中:Lcll为逆向可变车道长度,m;Lmin,Lmax分别为逆向可变车道长度最小,最大取值.
2 逆向可变车道交叉口信号配时优化方法
2.1 逆向可变车道交叉口车均延误模型
利用实时检测器获取初始排队长度与交通量等交通状态,以常规十字信号交叉口为例,周期内流向i在时刻t的驶离车辆数di(t)与此时的交叉口流向通行权、到达车辆数以及初始排队车辆数有关,主要基本情况可分为以下三种(一般忽略右转流向).
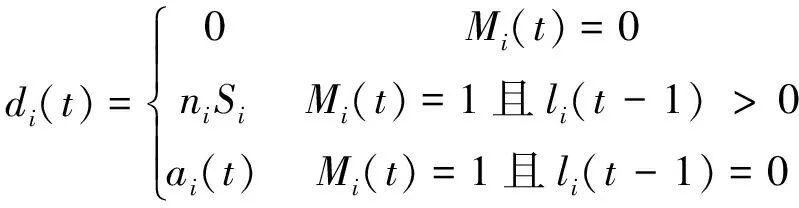
i=1,2,…,8
(4)
式中:i为逆向可变交叉口流向编号,依据图1中i从1到8分别代表东进口左转,西进口直行,南进口左转,北进口直行,西进口左转,东进口直行,北进口左转以及南进口直行;di(t)为周期内流向i任意时刻t的驶离车辆数,pcu/s;ni指i流向常规车道数;Si指i流向单条车道饱和流率,pcu/s;ai(t)为预测到的流向i任意时刻t的到达车辆数,pcu/s;Mi(t)为i流向在时刻t时的通行权,当Mi(t)取1时,为i流向在时刻t具有通行权,当Mi(t)取0时,为i流向在时刻t不具有通行权;li(t)为i流向在任意时刻t时的排队数.
逆向可变车道交叉口直行流向的计算方法与常规交叉口计算方法相同,后续对左转流向进行分析即可.逆向可变车道交叉口运行方式对左转车道饱和流率存在一定的影响,逆向可变车道可通过实地调查对饱和流率进行修正.
在左转主信号绿灯开始后的最初ge1内,逆向可变车道与常规左转车道全部以饱和流率释放,由于逆向可变车道的开启对常规左转车道存在一定的影响,经过实地调查抽样取均值可得常规左转车道修正系数Kl=0.87,因此左转流向饱和流率为ncllScll+KlnlSl,在ge1秒后,逆向可变车道驶离流率与到达流率相同,进口道饱和流率下降至nlSl.因此进口道的左转通行能力应为
(5)
式中:ncll,nl为逆向可变车道数及常规左转车道数;Scll,Sl为单条逆向可变车道饱和流率及单条左转车道饱和流率;ge,ge1为进口道左转主信号有效绿灯时间及可完全以饱和流率释放时的绿灯时间段,因此进口道平均饱和流率S为
(6)
因此S1称为逆向可变车道的有效饱和流率,其与逆向可变车道数ncll及逆向可变车道长度Lcll有关,即:
(7)
式中:Lpcu为平均每辆车占据的车道长度,一般取6 m.当逆向可变车道足够长或者相位有效绿灯时间足够短时,逆向可变车道即可视为达到完全的饱和流率值,即可视为完整的左转车道,因此不同逆向可变车道长度下的饱和流率变化可通过上式进行计算.
对于逆向可变车道交叉口左转车流向而言:

i=2,4,6,8
(8)
式中:P(t)=1为逆向可变车道在任意时刻t下具有通行权,P(t)=0为逆向可变车道在任意时刻t下不具有通行权;ncll,nl为逆向可变车道数量及常规左转车道数量.根据车辆累计算法,t时刻的排队长度与车辆到达流率、驶离流率以及初始排队数有关,则i流向周期内任意时刻t+Δt的排队长度为
li(t+Δt)=ai(t)+li(t)-di(t)
(9)
此时某一时刻的停车数量之和为车辆在该时刻产生的总延误,则周期内任意时刻的停留车辆数之和为周期总延误,则周期内逆向可变车道交叉口车均延误为
(10)
2.2 信号配时优化模型
1) 目标函数
(11)
2) 约束条件 ①主信号约束 对逆向可变车道交叉口主信号配时参数应满足其基本取值范围要求,即
Cmin≤C0≤Cmax
(12)
(13)
gemin≤gej,j=1,2,3,4
(14)
式中:j为逆向可变车道交叉口相位编号;Cmin,Cmax为周期的最小最大值,取45 s与120 s;gej为第j相位有效绿灯时间,s;L为信号周期总损失时间,s;gemin为最小有效绿灯时间,取10 s.
2) 相位相序及预信号约束
图6 逆向可变车道交叉口相位相序及预信号约束
由于南北直行车流不会影响逆向可变车道,当南北左转相位末的最后一辆车驶过逆向可变车道时,预信号绿灯即可开启.此外,预信号绿灯最晚开启时间应至少保证东西左转相位开启时驶入逆向可变车道的第1辆左转车能到达并驶出停车线.假设车辆匀速通过交叉口,则预信号绿灯开启时间与第2相位的开启时间差Δt1为
(15)
逆向可变车道的通行功能由进口道左转转变为出口道.在东西直行相位开始前,须清空逆向可变车道上的左转车辆.预信号绿灯提前结束的最小时间Δt2主要取决于逆向可变车道长度和车辆速度,即
(16)
(17)
式中:Lcll,lm,vmin分别为逆向可变车道长度,m;车辆驶过交叉口内部的距离,m;车辆驶过交叉口的最小速度,m/s.
3) 模型求解 本节利用自适应模拟退火算法进行求解,具体操作步骤如下.
步骤1系统随机产生初始解g0,设置初始温度为T0,设置概率函数以接受新解,设置退火次数.
步骤2系统按照满足逆向可变车道交叉口主预信号约束式(12)~(18)的随机扰动以生成新解g′,并计算新解的目标函数值E(g′),同时计算新解与原解之间的目标函数变化量ΔE.
步骤3若ΔE<0,则接受新解g′和新的目标函数值E(g′),若ΔE>0则以概率P接受新解g′及新目标函数值E(g′).
步骤4根据设定的降温方式更新温度Ti.
步骤5重复步骤2~4,直到搜索出全局最优解或达到了所设置的最大迭代次数.
步骤6停止退火过程,输出最优解g′=(ge1,ge2,ge3,ge4).
3 实例分析
3.1 仿真方案设计
1) 几何渠化条件 古田四路长丰大道交叉口几何渠化条件为:北进口从道路内侧至外侧分别为1逆向可变车道+2左转车道+2直行车道+1右转专用道;东进口从道路内侧至外侧分别为1左转车道+3直行车道+1右转专用车道;西进口与南进口几何渠化设置相同,从道路内侧至外侧分别为1左转车道+2直行车道+1右转专用车道,具体示意图见图7.

图7 古田四路长丰大道交叉口
2) 仿真参数输入 在VISSIM仿真模型中,设置机动车期望车速为45~60 km/h,黄灯时间和全红时间分别3 s和2 s.仿真时间设为11 700 s,并且在900~4 500、4 500~8 100、8 100~11 700 s时段分别输入交叉口在21:00—23:00,12:00—14:00及17:30—19:30实地采集的低峰期、平峰期以及高峰期流量,输入的流量值见表1.同时,为避免路网在仿真前期加载流量对仿真结果产生影响,仿真结果采集时间为900~11 700 s.

表1 VISSIM各仿真时段流量输入
3) 仿真信号控制模式 本文以定时信号控制方法、文献提出的动态控制模式与本文提出的优化方法进行仿真对比.其中定时控制采用高峰期开启逆向可变车道,低峰期及平峰期选择关闭逆向可变车道,并利用模拟退火方法对输入流量计算信号配时方案.动态控制模式为逆向可变车道动态切换及信号控制方法,具体详细优化见相关文献[7].本文优化方法对开口位置进行动态调整并利用模拟退火算法进行信号配时优化.
3.2 结果分析
通过运行VISSIM仿真软件及利用MATLAB语言接入COM口实现逆向可变车道交叉口连续仿真,获取3种控制模式下的逆向可变车道左转平均延误、平均排队长度以及交叉口车均延误的变化,具体对比情况见图8.
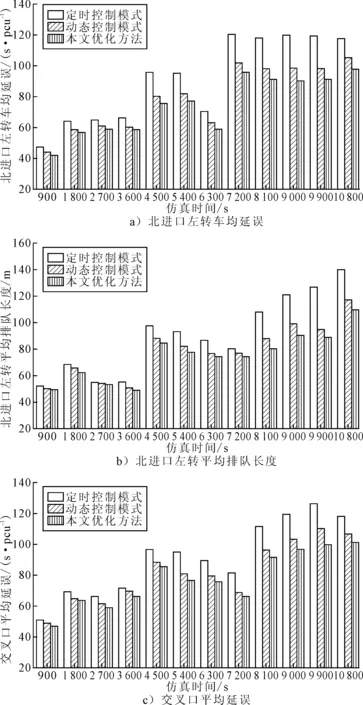
图8 逆向可变车道左转平均延误、平均排队长度以及交叉口车均延误对比图
从整体上看随着仿真时间的增多,输入流量越大,延误与排队长度均增加,增加幅度与流量也成正比.对于本文提出的开口动态调整优化方法而言,较动态控制模式与定时控制模式分别减小了1.8%~8%与9.2%~24.7%,且随着流量的增加,减小左转平均延误的幅度则越大.逆向可变车道左转平均排队长度较动态控制模式与定时控制模式分别减小了1.7%~8.9%与3.2%~29.9%,且随着流量的增加,左转平均排队长度减小的幅度也越大.
对于交叉口平均延误而言,3种控制模式下逆向可变车道左转平均延误随着仿真流量的增加而增加,在低峰期、平峰期与高峰期时间段,本文提出的开口控制方法交叉口车均延误比动态切换控制模式下的交叉口车均延误分别减少了3.6%,4.3%和6.4%,相比定时控制模式分别减少了8.4%,16.3%和18.1%,交叉口的整体运行效率提高,见表2.由表2可知:随着流量的增大,本文提出的开口动态调整方法效果越佳,改善程度越大.

表2 本文优化方法与其他控制模式运行效率对比
4 结 束 语
本文提出了逆向可变车道交叉口开口动态调整及信号配时优化方法,依据不同的交通需求对开口进行动态调整优化,以车均延误最小为目标构建了信号配时优化模型,并利用自适应模拟退火算法进行求解.结果表明:本文提出的逆向可变车道开口动态调整及信号配时优化方法能够减少逆向可变车道交叉口延误,提高通行效率.交叉口左转通行效率改善程度随交叉口交通量的增大而提高,并且较定时控制模式与动态切换模式延误都更小,原因是开口动态调整策略合理地依据交通需求调整逆向可变车道长度,使逆向可变车道利用率更高.表明逆向可变车道开口动态调整方法能够充分适应交通流变化,相较于低峰与平峰期的应用效果更为适用于高峰期.由于应用逆向可变车道开口动态调整后可能会造成司机行车困扰并造成安全隐患,后期研究将考虑开口动态调整对逆向可变车道交叉口安全方面的影响.
