考虑最短周期配时的单点交叉口时段划分方法

虞春滨 罗宗胤 黄寒松

(苏州工业园区测绘地理信息有限公司 苏州 215000)

0 引 言

城市道路交叉口1 d内的机动车流量分布呈现一定的规律,准确刻画其变化趋势对于交叉口信号配时优化有着重要意义[1-2].多时段划分就是根据1 d内交叉口交通流量的变化规律,将1 d划分为成多个不同的控制时段,每个时段采用相同配时方案的一种信号优化过程.一般的实现方式为,首先对路口全天进行多时段划分,然后进行多时段方案设计,但都未考虑方案设计阶段对于全天多时段划分产生的影响[3].目前对多时段划分的研究算法包括启发式搜索算法和聚类算法,主要集中在聚类算法层面.这两种方法相比传统经验法更加科学,通过数据驱动能够满足城市模式变化需求.其中启发式搜索算法适用于较大数据的分类处理,但是模型相对复杂、参数较多,对于较小的样本实现较为困难.聚类算法可以对简单的分类问题进行快速分类,参数相对较少,但是对于处理较大规模及高维度的数据较为困难.本文涉及问题的规模相对较小,故选择聚类算法实现快速分类.

Hause[4]提出将层次聚类方法应用到交通控制时段划分中,同时考虑交叉口流量数据及时间占有率,通过数据挖掘确定时间间隔,但无法确定划分时段数目.Wang等[5]针对层次聚类中需要大量数据以及计算密集的问题,提出将k-means非层次聚类方法应用于时段划分中,通过各个进口车道的流量数据进行时间转换点的识别,但聚类数目需手动设置,且没有考虑时间连续性问题,划分结果需要人为进行二次调整.Nedal[6]考虑到时段划分数量确定需要进行仿真并且涉及聚类性能指标,为简化其过程提出了基于减法算法确定时段划分数量,利用k-means进行多时段划分.王春娥[7]基于交叉口的交通总流量,通过C均值聚类分析进行多时段划分.曹成涛等[8]考虑到时段划分存在较强的主观性,提出了基于交通流时间因素的有序聚类算法.于德新等[9]通过对模糊C均值算法在时段划分方面进行相关限制,提出了一种基于改进模糊均值的时段划分方案,并且可以自动确定聚类数量.

上述研究都是基于交叉口流量或占有率数据作为输入变量进行时段划分,未考虑到时段划分的目的是进行多时段配时方案设计,而配时方案设计又会影响时段划分的结果.一般配时方案设计需要考虑行人过街及其他特殊需求,保证某一方向最短的绿灯时间,即使此刻机动车流量很小.这会导致最终的配时方案和时段划分结果与实际不符,而考虑最短运行时间限制可以弥补单独使用流量作为输入的不足.文中预先处理交叉口流量,将获得的设计配时方案作为输入,同时考虑方案最短运行时间的限制,通过SOM聚类方法进行快速时段划分,获得全天时段划分和设计配时方案.

1 理论基础

1.1 SOM神经网络

自组织特征映射(self-organizing feature map,SOM)神经网络,是一种无监督竞争式学习的前馈网络.图1为二维阵列SOM网络模型,也称为Kohonen Network,由输入层和输出层组成.每个输入节点与输出节点通过连接权值wij联系.

图1 二维SOM网络模型

1.2 SOM聚类训练过程

对于输入向量X=(x1,x2,…,xn)T,建立一个有m个输出节点的二维网格.具体的SOM学习过程可以归纳为以下步骤.

步骤1设置变量和参数 输入向量为权值向量,Wi=(wi1,wi2,…,win)T,n=1,2,…,m.设迭代总数为N.

步骤2初始化 将权值向量Wi进行初始化,并设置学习率η0;对权值向量初始值Wi(0)和所有的输入向量X进行归一化处理.

(1)

步骤3采样 从输入空间选取训练样本X′.

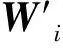
(2)

步骤5近似匹配 按照欧式距离最小的标准选取获胜神经元c.

(3)

步骤6更新 对获胜神经元拓扑领域内的兴奋神经元进行更新.定义神经元j在t时刻和t+1时刻的权值向量分别表示为Wj(t)和Wj(t+1).t时刻的学习率为η(t).

Wj(t+1)=Wj(t)+η(t)hj,i(X)(t)(X-Wj(t)),

t=0,1,2,…,N

(4)

步骤7归一化 对更新后的权值向量再次进行归一化处理.

(5)

步骤8终止条件 判断迭代时间t(迭代次数)是否超过N,如果t≤N,转到步骤3,否则结束迭代.

2 模型构建

2.1 最短周期计算方法

国内外学者对于多时段划分都是基于路口流量数据直接进行时段划分研究,忽略了某些限制参数对于结果的影响.事实上,路口配时方案的设计与交通参数限制有关,例如,最短行人过街时间、最短绿灯时间等,见图2.由图2可知:未考虑参数影响,易将时段划分为多个不连续的时段;考虑了参数限制影响后,虽然某两个时段流量有一定变化,但最短绿灯时间长度的配时都已经满足实际需求,因此这些时段应划为同一类.

图2 是否考虑参数限制对分类结果影响示意

据此,本文提出了一种考虑最短周期配时的单点交叉口时段划分,考虑各个进口车道流量和参数限制,将时段划分的最终目的(配时设计)提前至时段划分中,两者相结合使得时段划分具有实际指导意义.本文根据绿信比与流量比的关系,参考已有周期模型,提出了如下最短配时计算方式.

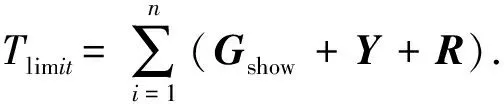
步骤2计算满足通行能力需求的最短周期 ①输入单点路口各个相位流量比,λ=(λ1,…,λi,…,λn);②计算满足通行能力需求的最短周期,Tcapacity=‖L‖1/(1-‖λ‖1/θ),θ∈(0.5,1),‖‖1为向量的1范数,下同,θ为超参数,保证设计流量比大于实际需求流量比,记设计流量比为λdesign=(λ1/θ,…,λi/θ,…,λn/θ).

2.2 损失函数构建

时段划分需满足时间连续性,同时需考虑信号机切换次数的影响,因此对于聚类结果进行二次优化,构建了以下损失函数.根据已有文献,多个方案切换时、交通流量时间序列以及实践中信号机切换方案机制的问题都会对路段交通流产生一定影响.结合实践经验,损失函数中的系数α1、α2相对于整体影响较小,而β1、β2相对整体影响较大.特别对于β2,信号机频繁切换方案对于交通流影响较大,因此其权重设置一般较大.

argminc=C(α1F1(·)+α2F2(·)+

β1G(·)+β2H(·))

(6)

I={i|i为需要调整方案的时段}

(7)

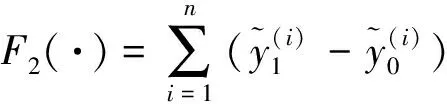
(8)

(9)

(10)

Y(i-1,i)+Y(i,i+1)≥0

(11)

(12)

3 实例应用分析

选取江苏省苏州市昆山市中华园路-柏庐路作为试验路口,该路口为典型的十字信号控制路口.基础数据为2022-02-28交叉口全天进口车道交通流量,整理得到每15 min进口车道的流量,如00:00—00:15,南直行200 pcu,北直行180 pcu.

全天除早高峰外均为标准四相位控制(南北直、南北左、东西直、东西左),其中早高峰为(南北公交优先、南北直、南北左、东西直、东西左).南北公交优先相位:相位内只有南北方向的公交车可以优先通行,社会车辆禁止直行和左转,假定忽略公交优先影响,则公交优先通行时间对于整个周期而言可以看作是全红时间,由于增加了损失时间,整个配时计算周期会适当增加,但最终配时结果可以将其中公交优先相位还原,即5个相位,其他相位依旧满足模型约束.为简化研究,将南北公交优先相位9 s归为南北直行的损失时间,则全天为标准四相位控制.将流量数据处理获得每个统计时间内的流量比,流量比=15 min相位最大流量/(单车道通行能力×车道数×0.25).

设置最短周期计算参数Gshow=(40,16,35,16),Y=(3,3,3,3),R=(3,3,3,3),非早高峰L=(2,0,2,0),早高峰L=(11,0,2,0),θ=0.85.通过2.1的最短配时方法计算得到全天每15 min的单点配时方案.然后通过Python中SOM包进行聚类,并通过编程进行二次优化处理.其中输出层参数为8×8阵列,迭代次数为30次,每次迭代为5个样本.损失函数中的系数设置为α1=0.1、α2=0.5、β1=5.0、β2=20.0,默认每个单点方案至少运行30 min.最终可以得到损失最小下的时段划分方案及配时方案,见图3a)和表1.表1为各个相位的显示绿灯时间,周期为包含黄灯和全红时间.

表1 配时方案 单位:s

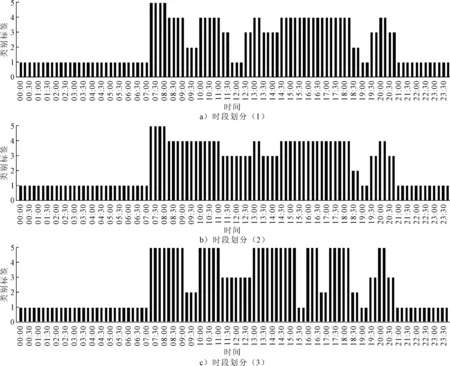
图3 时段划分

图3a)中的时段划分结果表示为:全天一共分为5个标签类别,同时识别出早高峰(07:15—08:15)、中午低峰(11:45—12:15)、晚高峰后期(20:00—20:30)及夜间的差异.通过实际观察发现,该路口早高峰南北流量在全天出于较高水平,白天平峰和晚高峰差异不大,而在20点多车流量再次上升至白天平峰水平.但是图3a)中的方案总切换次数为16次,这对于实际信号机系统而言切换次数过多.

在生产实践中,需要尽可能减少方案切换次数,同时每个时段内符合流量的变化趋势.因此本文重点对β2的敏感度进行分析.进一步研究发现,若保持其他参数不变,提高β2的值至40.0,即增加频繁切换的损失,可以获得新的时段划分,见图3b).图3b)划分结果中将某些时段的方案与相邻方案进行合并,而在图3a)中未能表现,原因为当提高切换方案次数增加损失权重后,减少的切换方案损失大于其合并方案后增加的损失,因此这些方案进行了合并.若持续增加β2的数值,理论上会获得全天一个配时方案的极端情况.同理,适当减少β2的值至10.0,见图3c).由图3c)可知:方案切换数量明显增加,主要原因为切换方案增加损失下降,同时提升方案以及更新类方案损失权重较小,因此将类别标签4全部提升为类别标签5,由此可见其敏感度相对较大.此外,α1,α2分别表现为提升方案损失和更新类方案损失,方案周期的增加与合并容易造成路口延误的增加或者空放现象;β1为切换方案增加损失,表现为前后变化周期差值的代价,相邻方案周期差值越大,损失越大,对于最终时段划分结果影响越大.因此需要根据实际进行参数的选取和调整,工程实践中重视切换次数以及切换损失,可以适当提高其比重,否则可以适当降低.

此外,模型首先需计算全天每15 min配时方案,然后进行SOM聚类,聚类数量由于算法特点每次会发生一定变化,通过经验设置最小分类数目,以及过二次优化处理后可以确保在同一参数设置情况下的结果一致性,因此模型和算法具有相对稳定性.

为验证试验方案的可行性,将图3b)和表1的方案应用到实际信号机控制系统中,选取对照组为目前已有配时方案,主要以工程师经验进行时段划分以及方案设置,试验组为本文方法计算得到的结果.通过滴滴平台获取试验前5个工作日及试验日的全天路口停车延误指标,见图4.

图4 路口停车延误指数

由图4可知:试验组当日的全天路口停车延误整体在对照组的下方,路口停车延误下降近17.5%,一定程度说明采用本文方案进行时段划分有利于降低路口整体延误,同时时段划分更加切合实际情况,为更加精准地进行单点交叉口时段划分提供一个可行的方向.

4 结 束 语

本文提出了一种考虑最短周期的单点交叉口时段划分方法,弥补了传统方法只考虑交叉口流量的不足,将最终设计配时方案阶段考虑至时段划分中,同时增加限制参数,可以快速获得最短周期的设计配时方案,进一步可以作为自适应控制路口的基本方案配置.试验结果证明了该方法的有效性和可行性.