基于极点配置法的离网光伏逆变器控制系统设计及仿真*

詹新生，王 毅

（徐州工业职业技术学院，江苏徐州 221140）

0 引言

能源利用与环境保护是影响中国经济和社会可持续发展的突出问题。在这样的背景下，大力发展新的可替代能源已成为当务之急。太阳能有着永久性、储量大、清洁无污染等突出优点，是目前可利用的最佳能源选择之一，显示出无比广阔的发展空间和应用前景。在政策的支持与推进下，我国的新能源光伏发电产业得到了长足的发展[1-3]。

逆变器是光伏系统中的核心部分，分为离网与并网逆变器。离网逆变器用于光伏离网发电系统，主要将直流电变成交流电供交流负载使用。光伏离网逆变器本身不具有储能功能，与电网断开连接后可以独立工作，相当于一个独立的小电网，主要控制自己的电压源。可承载电阻、电容、电机电感等负载，快速应变和抗干扰，适应性强，实用性强。是停电应急电源和户外电源的首选电源产品，适用于电力系统、通信系统、铁路系统、船舶、医院、商场、学校、户外等场所。可连接市电给电池充电。

传统在设计光伏逆变器双闭环系统时需要按照先电流内环、后电压外环这样逐步设计，步骤较为繁琐，如在忽略电流环的反电动势、电流环小惯性环节的降阶环节、电流环闭环传递函数的降阶环节中均做出工程近似，满足这些环节需要满足一些条件[4]。因此设计出的系统动态特性往往不够理想，基于此，本文提出采用极点配置法来设计电压外环与电流内环的参数，极点配置法的本质是用比例反馈去改变原系统的模式，从而满足设计规定的性能参数要求，极点配置法可以把系统的闭环极点配置到希望的极点位置上，从而可以简化设计步骤，参数计算容易，而且与性能指标之间有直接的量化关系，可以实现良好的静态与动态特性。

本文详细给出系统中核心元件的参数设计方法，控制方式上使用双环控制模式（电压外环，电流内环），采用极点配置法设计两个环路的控制系数[4]，同时采用了前馈控制，可以加速系统响应速度，减小偏差，提高系统的稳定性与准确性。为了验证上述理论分析和设计，基于专用电力电子仿真软件PSIM 搭建了电源系统的仿真模型，对所构建的离网逆变器系统进行了仿真验证，各项测试表明本文设计的系统动态静态特性良好，鲁棒性强，达到了预期设计目标。

1 离网逆变器控制策略

高质量的逆变电路要求输出波形稳态精度高、动态响应快。开环控制的逆变器难以达到这两方面的要求，而闭环控制的逆变器精度高、输出电压电流可控、受系统参数变化影响小，因此闭环控制是逆变电路所必需的。目前较为成熟、控制效果较好的控制方案有PID 控制、重复控制、无差拍控制等。由于PID 控制能兼顾控制系统的稳态性能和动态性能，因此选择的控制方案是PID控制。

PID控制分单闭环和双闭环控制，其中PID单闭环控制的动态响应较慢、对负载的扰动抑制有一定的局限性，所以在控制部分采用双闭环控制，双闭环控制的优点主要有如下3点[5-6]：（1）可以消除LC滤波电路中的谐振峰值；（2）将电容电压作为一个反馈量，对于负载扰动可以迅速地进行补偿，提高系统抗负载扰动性，从而提高了系统的动态性能；（3）采用电流作为反馈量，使得系统在突加重载的情况下，可以对产成的过流进行补偿，有效地提高了系统抗冲击电流的能力。

逆变器的电流内环可以采样电感电流或者电容电流。在电感电流内环控制中，负载电流作为外部扰动信号，在电流内环外，所以控制系统抗负载波动的能力差，因此逆变器的动态性能不甚理想。而采样电容电流作为内环的控制系统，电容电流可以被瞬时控制，从而使输出电压因电容电流的微分作用而可以得到矫正，因此这种模式的抗负载扰动能力强、动态性能好，但是不能对功率管进行过流保护。考虑上述两种控制策略的优劣，本文采用带负载电流前馈的采样电感电流内环、输出电压外环的控制策略。

离网逆变器控制系统整体控制框图如图1 所示。图中Vi为输入电压，C1为输入电容，T1、T2、T3、T4为开关管，其中，T1 与T2，T3 与T4 为两组互补的开关管，r为电感L 的等效电阻，C 为滤波电容，Ro为模拟负载。L、C为输出侧的低通滤波器。

图1 带有前馈控制的离网型全桥逆变器系统控制框图

本文设计一个10 kW 的离网光伏逆变器，输入电压范围为360～420 V，输出电压为单相220 V（有效值），频率为50 Hz，负载功率因数为0.8，输出电压波形畸变系数小于0.05，开关频率为20 kHz。

2 元件参数设计

2.1 滤波电感设计

取电感的在工频下的电压值不超过占输出电压有效值的3%[5-6]，电流波动系数为0.2，代入式（1）中：

2.2 滤波电容设计

设计LC 滤波器截止频率fc为开关频率fs的10%，可获得较好的滤波效果，根据公式：

代入数据，取C=20µF。

3 控制系统模型

3.1 脉宽调制系统

逆变器控制系统中脉宽调制系统[7]如图2所示。

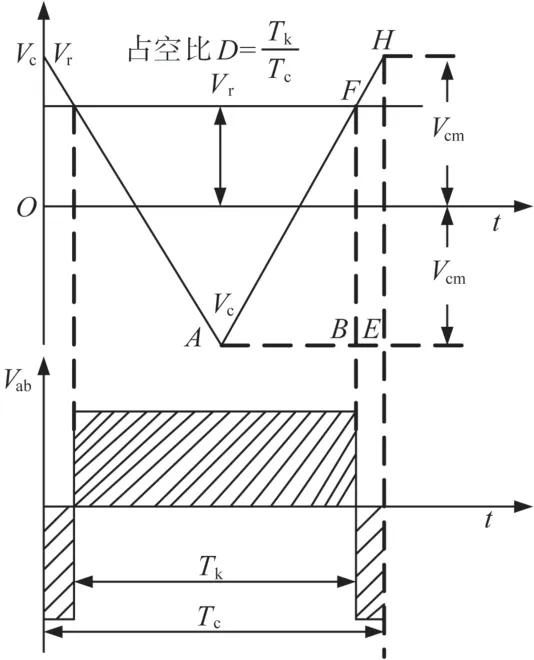
图2 调制波到输出电压模型

图中Vr为调制波，Vc为载波。在一个载波周期Tc内，在Vr＞Vc期间，T1和T4处于通态，Vab=VD；在其余（Tc-Tk）期间，Vr＜Vc，T2和T3处于通态，Vab=-VD。由图中的几何关系可得到T1、T4同时处于通态的占空比：

在一个载波周期Tc，输出电压的平均值为：

将占空比D代入上式可以得到调制波到输出电压的模型：

3.2 LC滤波器系统模型

对于LC滤波器部分[8]，满足式（8）：

则可得到结合脉宽调制与LC滤波器部分的模型如图3所示。

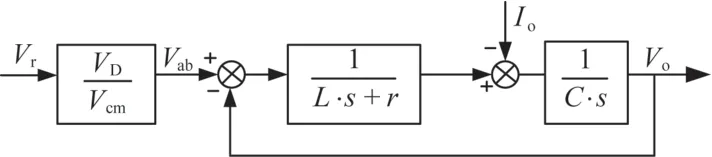
图3 LC滤波器系统控制框图

在PSIM 中构建上述滤波器的模型，通过交流扫频法得到该模型的伯德图如图4 所示。从伯德图和阶跃响应可以看出，该系统相角裕度约为2°，稳定裕度较小，因此需要添加控制器做闭环控制。

3.3 系统整体控制框图

综合上述分析，可以得到离网型单相全桥双闭环逆变器的整体控制框图，如图5 所示。为了抵消负载电流对电压回路的扰动，将负载电流加入电流回路的输入端，即电流的前馈控制。

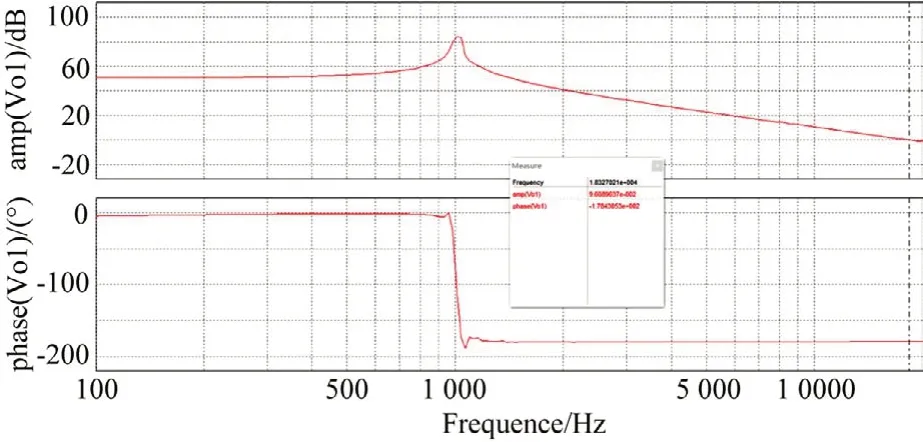
图4 LC滤波器伯德图

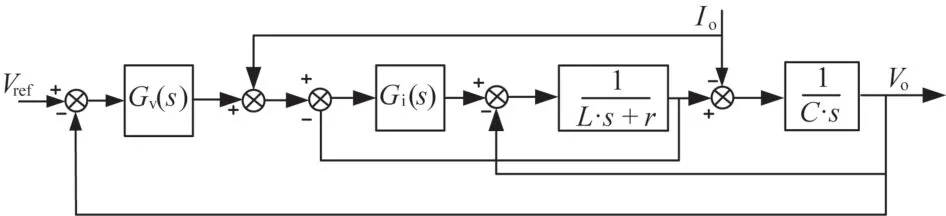
图5 离网逆变器整体控制系统

逆变器的电流前馈控制系统可以根据扰动或给定值的变化按补偿原理来工作的控制系统，其特点是当扰动产生后，被控变量还未变化以前，根据扰动作用的大小进行控制，以补偿扰动作用对被控变量的影响。电流前馈控制系统运用得当，可以使被控变量的扰动消灭在萌芽之中，使被控变量不会因扰动作用或给定值变化而产生偏差，它较之反馈控制能更加及时地进行控制，提高系统的响应速率[9]。

4 双闭环系统参数设计

按照前面的分析，本文采取极点配置法[9-14]设计电流内环与电压外环的比例-积分参数。

电压调节器和电流调节器传递函数如式（9）所示：

推导得图5的系统的传递函数如式（10）所示：

其中，特征方程如式（11）所示：

利用极点配置法，假设该系统的闭环主导极点和非主导极点如式（12）～（15）所示：

那么控制系统的期望特征方程如式（16）所示：

比较特征方程的系数如式（17）所示：

根据非主导极点的定义[15-16]，取m=8，n=10。取最佳阻尼比ζ=0.707，ω=2 500 rad∕s。代入式（1）～（2）求得主电路参数并联立式（7） ～（14） 可求得：k1p=0.01，k1i=150，k2p=0.3，k1i=2 000。

基于上述分析，在PSIM 仿真软件可以得到系统的伯德图与阶跃响应，如图6 所示。从波特图和阶跃响应可以看出，该系统相角裕度足够，表明控制器的设计基本符合预期。

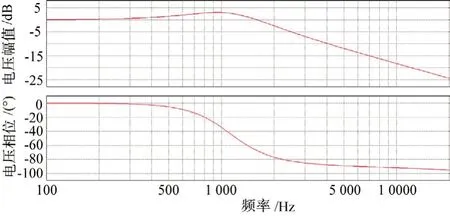
图6 控制系统伯德图

5 仿真及结果分析

基于前面的分析，在PSIM软件中搭建离网逆变器的控制系统仿真模型[17-20]，如图7所示。系统设计要求如下：（1）输入电压为360～420 VDC；（2）输出电压为单相交流220 V；（3）输出电压频率为50 Hz；（4）额定功率为10 kW；（5）负载功率因数为0.8（感性负载）；（6）输出电压总谐波畸变（THD）小于5%；（7）开关频率为20 kHz。

图7 离网逆变器仿真模型

5.1 性能指标验证

仿真的输出电压电流波形如图8 所示。由图中所示，输出电压电流波形正弦特性良好。使用PSIM 软件强大的仿真实验数据后处理功能，可以得到输出电压的有效值 为220.34 V，THD 为0.026 67%。输 出 有 功 功 率 为10.335 kW，负载功率因数为0.800 39（感性），性能均满足设计指标要求。

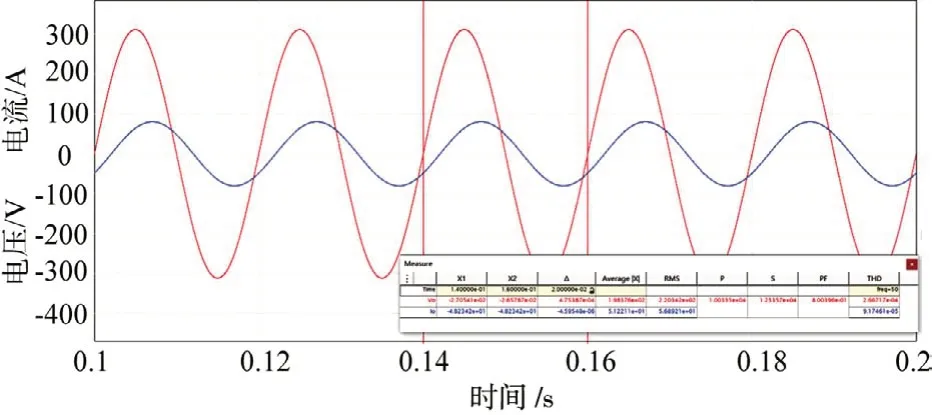
图8 系统输出电压输出电流

5.2 抗干扰测试

5.2.1 负载突变

仿真总时间设置为0.8 s，设置0.2 s 时突加负载，并联接入20 Ω电阻，在0.6 s时将加载的负载切除，输出电压与电流如图9 所示，从图中可以看出，0.2 s 后切入负载后，电流变大，输出电压基本保持不变，0.6 s 后将加载的负载切除后，电流恢复至原值，输出电压也保持基本不变，可见负载突变对输出电压的影响很小。

5.2.2 输入电压突变

仿真总时间设置为2.4 s，设置0～0.8 s 输入电压为400 V，0.8～1.4 s 输入电压为360 V，1.4～2 s 输入电压为420 V，0.8～1.4 s 输入电压为420 V，0.8～1.4 s 输入电压恢复为400 V，仿真波形如图10 所示，从图中可以看出输出电压也基本保持不变，可见输入电压突变对输出电压的影响很小。

图10 输入电压突变输出电压波形

6 结束语

本文首先分析了光伏离网发电系统的优势所在，指出了传统的设计光伏逆变器双闭环控制系统参数方法的繁琐与缺点。设计了一台10 kW 的离网全桥逆变器，给出单相光伏逆变器系统中核心元件的参数设计方法，采用极点配置法设计了控制系统的双环控制参数，并基于PSIM2021a 仿真软件平台构建了系统测试平台，各项的仿真结果表明设计的逆变器控制系统能均满足指标要求。同时也仿真了在负载突变和输入电压突变时情况下的输出电压，表明带负载电流前馈的双闭环控制抗干扰能力强，动态性能比较优越。因此所选择的控制策略是比较合理的，为进一步的硬件与软件设计打下了良好的理论基础。