基于拓扑优化和响应面分析的6030 龙门加工中心横梁轻量化设计

肖康利，曾凡洋，王 柱，王健林，王天雷

（1.广东艾普升智能装备有限公司，广东恩平 529499；2.五邑大学智能制造学部，广东江门 529020）

0 引言

随着数控技术的快速发展和科学的不断进步，数控机床已被广泛应用于工业领域［1］。高速龙门五轴加工中心主要面向大型复杂模具制造以及铝合金结构件的高速、高效、高精加工，是机械制造领域的关键加工装备［2］。机床的轻量化设计可直接减少不可再生能源、资源的消耗，有着重要意义［3］。轻量化是在保证机床静动态特性前提下，减轻机床质量，降低资源消耗和减少制造的成本［4］。横梁是龙门加工中心的主要支撑部件，其结构设计合理与否直接影响机床的整体性能［5］，研究横梁结构，提高加工中心整体性能成为了众多学者研究的重点［6］，文献［7］通过拓扑优化技术去除横梁结构的冗余质量；文献［8］以横梁的总体积为目标函数对横梁结构进行优化；文献［9 -18］针对不同用途加工中心的横梁采用有限元方法进行了静动态特性分析，拓扑结构、响应面分析、多目标优化和仿生结构设计等，对横梁及其筋板结构进行了优化，使横梁重量均不同程度得到减少，具有较好的实际应用价值。

本文采用Workbench对6030 龙门式加工中心概念模型（图1）中的横梁进行静动态特性分析，并在DX模块中检测参数选择的相关性，选取主要参数对横梁结构进行轻量化设计，在减小龙门中心横梁的质量并尽可能提升或维持龙门横梁静动态特性。

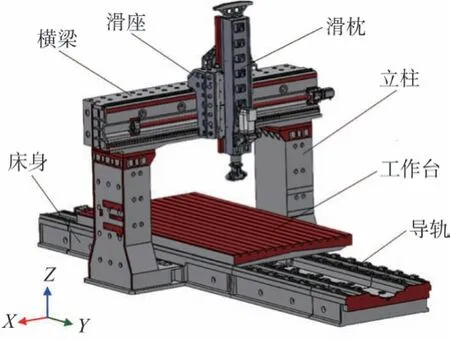
图1 6030 型龙门式加工中心三维模型

1 横梁静态特性分析

（1）前处理。横梁材料为HT250，材料密度为7 280 kg／m3，弹性模量为1.38 ×1011N／m2，泊松比为0.156。横梁网格划分采用自动网格划分，有限元模型的节点数是25 533，单元数是84 827。

（2）载荷计算。6030 型龙门式机床是定梁型结构，横梁两端底部通过螺栓与立柱连接。主轴部件通过横梁上的导轨与丝杆实现z 轴移动。在横梁导轨的基础上，滑枕安装在滑鞍中，通过主轴上的丝杆带动滑枕实现y轴位移。当主轴部件运动至横梁中间位置，且滑枕运动到最低点时，横梁将产生最大的弯曲变形。

铣削总切削力按下式计算：

式中：ae为铣削层深度；fz为每齿进给量；ap为铣削宽度；Z为铣刀齿数；D为铣刀直径；KFc为修正系数。

常用工艺采用的盘铣刀直径为150 mm，铣刀齿数为12 齿，铣削层用量为ae＝1.5 mm，每齿进给量fz＝0.3 mm，铣削宽度ap＝20。将上述参数代入式（1）得Fc＝1702.1 N。由式（2）可得各向切削分力Fx＝1 531.89 N，Fy＝1 191.47 N，Fz＝936.16 N。

（3）横梁载荷及边界条件。横梁载荷施加：主轴箱及滑枕质量G1＝180 kg，横梁上丝杆和电机的质量将其分别施加于支承座安装面G2＝36 kg 和电机座安装面G3＝72 kg，切削力用远程力代替，将G1、G2、G3加载到横梁上，再加上横梁本身质量。模型受力分析与载荷施加分别如图2 与图3 所示。工作时横梁固定不动，因而在模型底部施加固定约束。

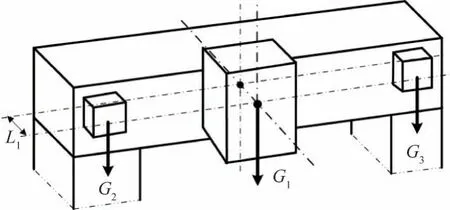
图2 力分析模型

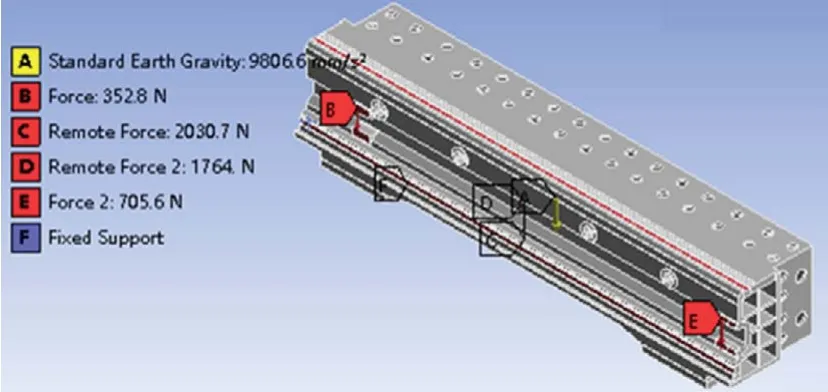
图3 横梁载荷

（4）求解结果。计算结果如图4 所示，分析可知，横梁最大变形发生横梁中部，最大总变形为11.202 μm，横梁最大应力为2.678 2 MPa，远小于该材料许用应力。上述分析结果为下面横梁结构优化提供对比。

2 横梁动态特性分析

对模型底部上施加固定约束，计算得前6 阶固有频率、变形与振型如表1 和图5 所示。分析可知，横梁1阶、2 阶振型均为整体摆动，3 阶振型才出现了扭转情况，主轴转速0 ～5 000 r／min，产生的旋转激励频率为100 Hz，小于横梁的1 阶固有频率；铣刀齿数为12 齿，加工时切削产生的激励频率为1 200 Hz，远高于横梁前6阶固有频率；前2 阶振型为摆动，没有发生扭转情况，不会产生受力不均现象，满足动态设计要求。

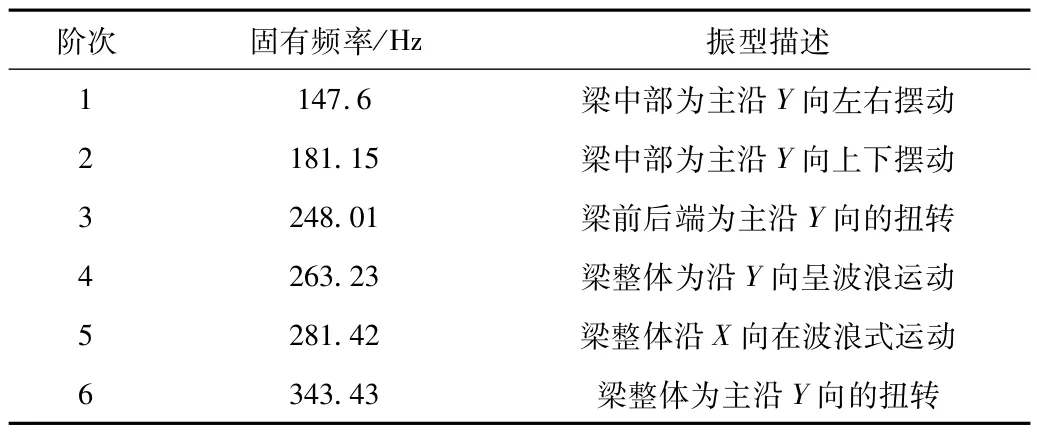
表1 横梁的6 阶固有频率、变形及振型

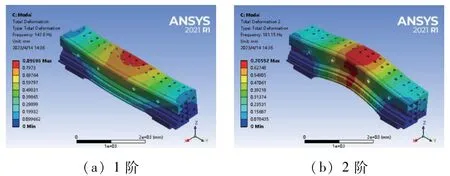
图5 原横梁模态分析

3 横梁的轻量化设计

3.1 横梁的拓扑优化

拓扑优化方法有很多，如渐进结构优化法、均匀化法和变密度法。本文采用变密度法，即将单元密度与材料弹性模量用函数方程来表达，并构建函数，去除非传力路径上的材料，保留传力路径上的材料，提高材料的利用率，实现减重设计。

选择ANSYS Workbench 中Topology Optimization 模块，导入静动态分析中所得数据。在target 中将固有频率和柔顺度的权重比例分别设置为0.6 和0.4。定义设计区域与非设计区域，如图6 所示。设置质量分数为70%，求解横梁的拓扑模型，得横梁拓扑结构优化模型如图7 所示。

图6 优化区域设计

图7 拓扑优化模型

拓扑优化得到模型需对结构进行重构设计，使其满足工艺等要求。根据拓扑优化结果建立重构模型和静力学分析结果如图8 和图9 所示，对比数据如表2 所示。

图8 横梁重构模型

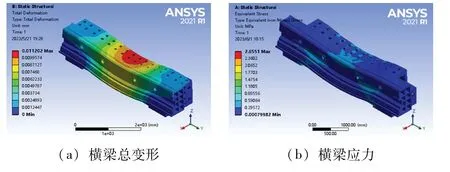
图9 重构后横梁静力学分析

表2 横梁结构优化的设计变量

优化前、后横梁质量分别为8 001.7 kg和7 582.0 kg，最大变形为11.313 μm和11.202 μm。分析可知，优化后横梁的质量减少了5.2%，达到了轻量化的要求。最大变形量略有下降，1 阶、2 阶固有频率略有提升。

3.2 横梁的响应面优化

采用响应面优化方法对影响横梁质量、1 阶固有频率、最大变形量、最大等效应力通过选取设计变量、实验设计、灵敏度分析等，然后通过遗传聚合法求解得各变量的响应面。最后采用MOGA 优化算法得到各变量最优尺寸组合。根据最优方案对横梁的尺寸进行重构，最后对优化前后参数进行对比，验证优化结果。

3.2.1 选取设计变量

设计变量的确定为结构参数化，本文设计变量选为横梁壁厚尺寸及各层肋板厚度尺寸，初步确定设计变量为7 个，如图10 与表2 所示。对设计参数进行灵敏度分析，并根据灵敏度值确定设计参数进行优化。

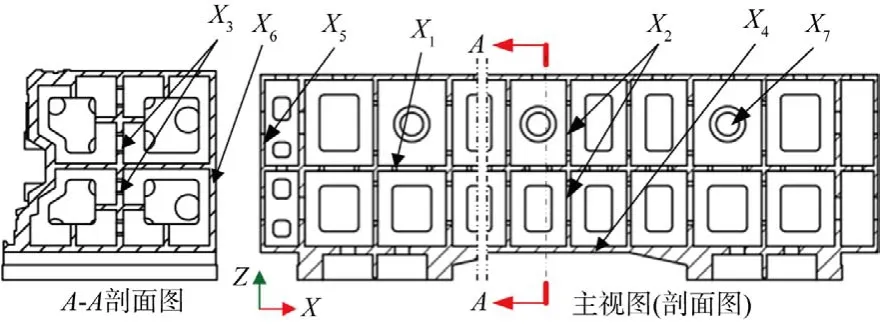
图10 横梁结构示意图

3.2.2 灵敏度分析

为获得1 阶模态频率和质量与每个设计参数的灵敏度值，将各设计变量进行参数化，实验设计时输入参数为各设计变量，输出参数为质量、1 阶固有频率和最大变形，可得灵敏度直方图，如图11 所示。

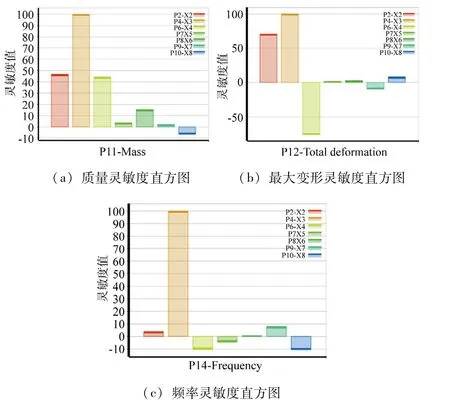
图11 灵敏度直方图

分析可知，X1、X2和X3对目标函数影响较大，因而选定为构造响应面优化的设计变量，如表3 所示。

表3 横梁结构优化的设计变量

3.2.3 实验设计

ANSYS Workbench中的Design Xplorer模块中提供了7 种试验设计方法，其中Box-Behnken 设计具有试验效率高、试验次数少以及可避免极端因素组合的优势。因此本文选择该方法对横梁进行试验设计。将横梁的质量、总变形量以及1 阶固有频率作为输出参数，系统自动生成了13 组样本数据，如表4 所示。

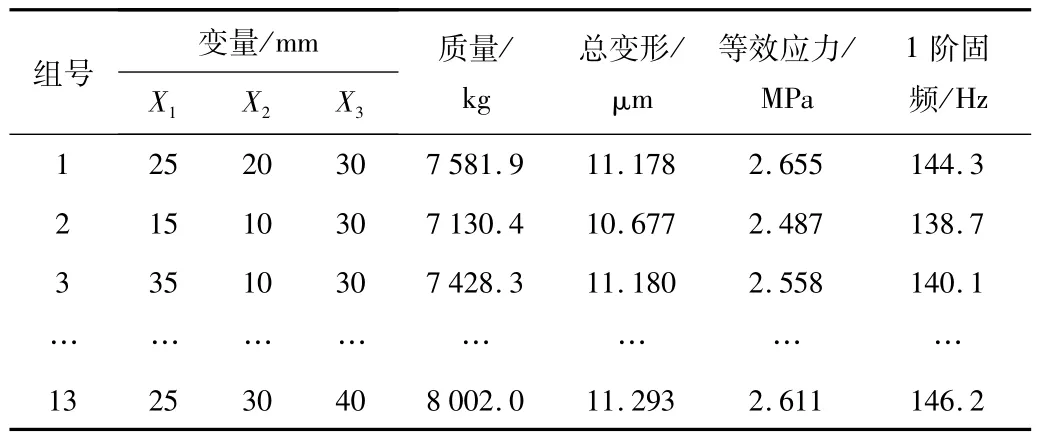
表4 试验设计样本及试验结果

3.2.4 响应面分析

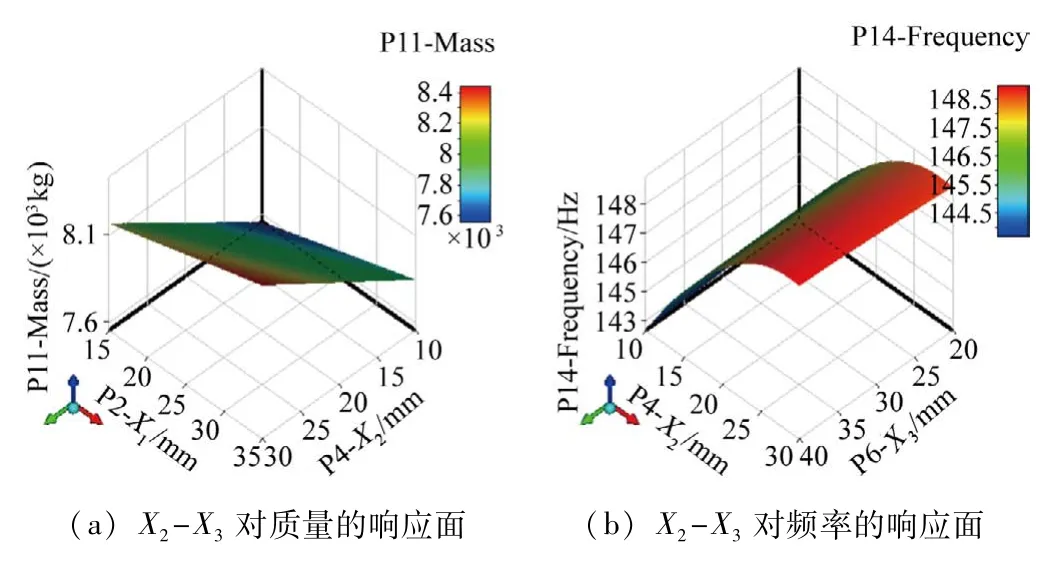
响应面分析法（RSM）是一种综合试验设计和数学建模进行实验寻优方法，可有效减少试验次数和因素之间的交互作用。常见的响应面类型包括遗传聚合、标准二阶响应面、克里金、非参数回归、稀疏网格和神经网络等，其中遗传聚合可处理带有空间相关性的数据，拟合精度高，可提供误差估计。本文选用遗传聚合法构造响应面模型，可得各设计变量与质量、总变形等效应力和频率3 个目标变量的响应面，图12 选取了X2、X3对目标变量的响应面。

分析全部响应面图可知：X1、X2、X3与横梁质量成线性关系，随尺寸增加一直增大；与横梁频率近似成线性关系，随变量尺寸增大而减少；与最大变形量的近似成线性关系，其变化随着尺寸增大一直减少。

3.3 多目标优化求解

此次优化设计的目的是在横梁1 阶固有频率不下降（最佳情况是频率提高）、最大变形量不增加（最佳情况是最大变形量减少）的前提下，实现横梁轻量化。因此将最大变形量最大等效应力、质量和1 阶固有频率作为优化目标。设计变量为之前定义的横梁的3 个变量，由此得横梁多目标优化的数学模型如下：

设计变量：X1、X2、X3。

设计约束：1 阶固频大于或等于144.36 Hz；最大静态等效应力大于或等于2.655 1 MPa；最大静态总变形小于或等于0.011 178 mm。

优化目标：使质量最小。

为最大程度实现减轻质量的效果，设置目标重要性，质量为higher，1 阶固有频率为lower，最大变形量的重要性为lower。在Design Exploration 模块下对横梁进行优化，系统寻找到符合优化目标的3 个推荐点，如表5 所示。分析可知，优化后第3 组质量为最低，为最优解，1阶固有频率为144.63 Hz，最大变形量为0.011 298 mm，等效应力为2.664 8 MPa，横梁静动态性能都有所改善。优化后横梁质量为7 383.7 kg，比优化前减少了198.3 kg，实现了减重优化目标。

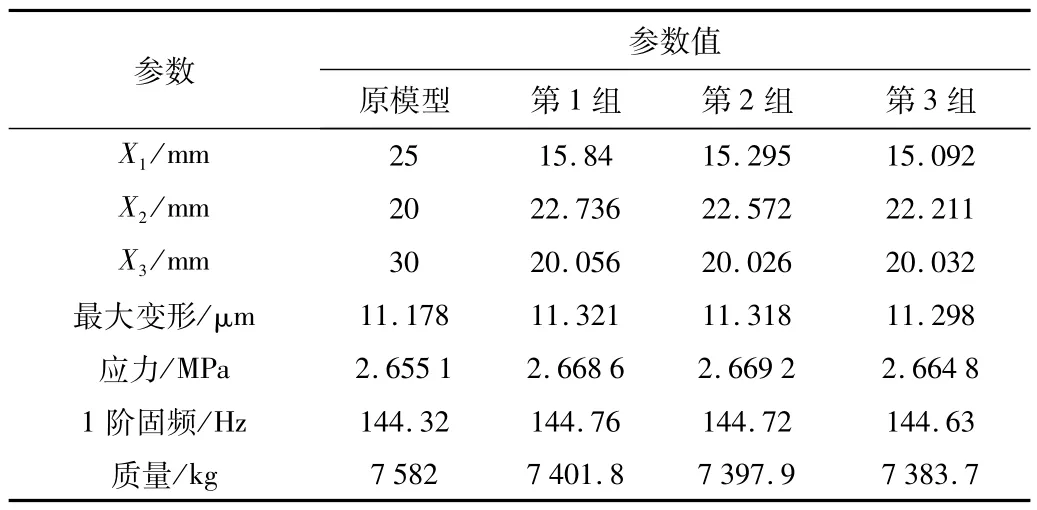
表5 优化结果

4 横梁优化前后对比

4.1 优化后横梁静态分析

根据上文所述，选定第3 组数据作为优化后参数，将尺寸圆整后取X1＝15 mm，X2＝22 mm，X3＝20 mm。对优化后横梁的静态分析结果如图13 和表5 所示。

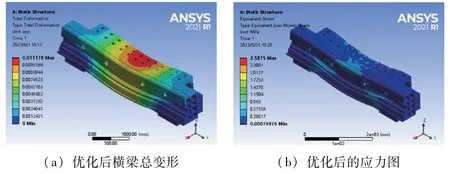
图13 多目标优化后静态特性分析结果

4.2 优化后横梁模态分析

对优化后的横梁进行模态分析，得前2 阶固有频率及振型如图14 所示，具体参数如表6 所示。分析可知，前2 阶的固有频率有小幅降低。

4.3 优化后横梁质量对比

通过测量优化前后横梁的质量，并进行对比，结果如表6所示，分析可知，优化后的横梁质量有了大幅减少，效果良好，实现了横梁轻量化的目的。综上所述，对6030型龙门式加工中心的横梁进行优化静态性能几乎不变。

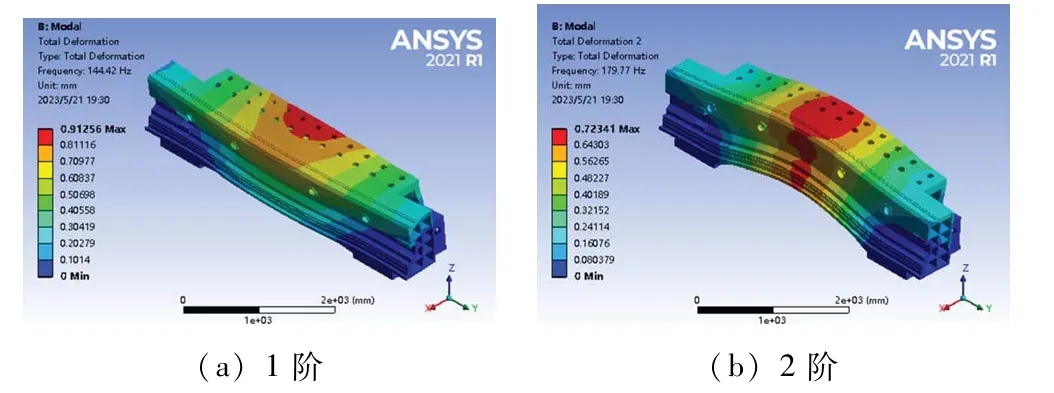
图14 优化后横梁前2 阶振型

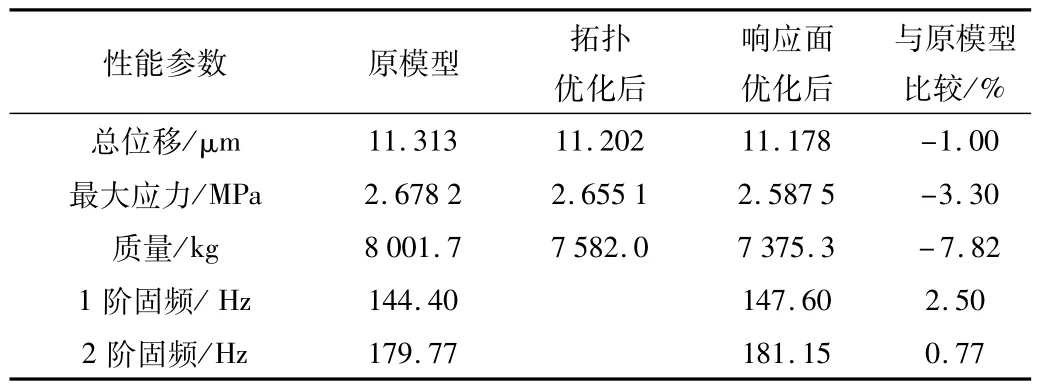
表6 优化前后参数对比

5 结束语

（1）分析计算了6030龙门式加工中心的横梁受力，采用ANSYS Workbench软件对横梁模型进行了静动态分析。

（2）采用拓扑结构优化方法实现了横梁材料合理分布；进一步采用灵敏度分析、响应面分析法对横梁结构参数，如壁厚尺寸及各层肋板厚度等尺寸进行了多目标优化。

（3）优化结果表明：原横梁质量为8 001.7 kg，经拓扑结构优化重构后为7 582.0 kg，继续尺寸优化后得最终为7 375.3 kg，比较原横梁的质量减少7.82%；横梁总变形则由初始11.313 μm减少到11.178 μm，下降了1.2%；最大应力值则由2.678 2 MPa 减少到2.587 5 MPa，下降了3.3%；最终优化后横梁1 阶固有频率为147.6 Hz，比较优化前横梁144.4 Hz略有提高。

本文采用的优化方法在保证原横梁总变形略有减少和1 阶固有频率有少许提高的前提下，质量得到了大幅减少，实现了轻量化设计的要求。