有限元建模方式对风机轮毂疲劳计算的影响

2023-11-13秦瑞冰赵春雨柳胜举李有亮黄文杰

机电工程技术 2023年10期

秦瑞冰，赵春雨，柳胜举，李有亮，许波，黄文杰

（明阳智慧能源集团股份有限公司，广东中山 528437）

0 引言

疲劳损伤是由于材料在交变载荷作用下发生微观损伤和裂纹扩展引起的，在循环载荷下，材料内部会形成裂纹，并随着循环次数的增加而扩展，最终导致材料失效［1-3］。疲劳损伤广泛存在于各种机械结构中，疲劳损伤的发生不仅会导致设备的失效，还会对人身安全产生威胁，而且在风力发电设备中，轮毂的结构强度直接决定风力发电机组的整体结构安全性和风机载荷的顺利传递，其具有更重要的作用，因此对风机轮毂疲劳损伤的研究具有重要意义［4-6］。

针对风力发电机组轮毂的疲劳损伤计算，国内外许多学者都已进行了研究。文献［7］研究了机械结构的疲劳强度计算与分析；文献［8-9］研究了风机复杂工况下的力学特性，并通过实际测量研究了等效风速与轮毂风速对功率的影响。何玉林等［10］计算了风力发电机组的轮毂在极限工况下的强度及疲劳工况下的疲劳寿命；朱涛等［11］采用有限元法对某兆瓦级风力发电机组轮毂进行极限强度分析，使用有限元软件对轮毂进行疲劳寿命分析。杨兆忠等［12］结合有限元和疲劳损伤理论，以轮毂为对象进行疲劳寿命的计算与研究。研究了单位载荷下有限元计算结果、疲劳载荷和材料S-N 曲线。文献［13-14］根据GL规范，利用有限元方法对轮毂进行静强度和疲劳强度分析，并且给出了轮毂材料S-N曲线的详细拟合过程。有效解决了风机轮毂强度计算问题，为轮毂结构优化奠定基础。

现在针对轮毂的疲劳计算方法，有螺栓连接与绑定连接两种建模方式，现有研究大多是在同一种建模方式下研究轮毂的疲劳损伤；为了研究绑定连接与螺栓连接两种建模方式对疲劳损伤计算结果的影响，本文通过建立绑定连接与螺栓连接两种有限元模型，对两种模型进行疲劳损伤计算，探究两种建模方式对疲劳损伤计算的影响，为后续风机轮毂的疲劳计算提供了理论依据。

1 有限元建模

以某兆瓦级风机轮毂为例建立有限元模型，对轮毂使用高阶单元进行建模，变桨轴承、主轴用低阶单元建模，并建立变桨驱动假体和10 m长的叶片假体；整体模型从叶片-变桨轴承-轮毂到主轴，约束主轴端面，3 个叶片采用相同的建模方式，根据GL 规范在叶根中心建立加载坐标系，并在加载坐标系原点建立加载点，加载点通过MPC力分布的方法与叶片顶端绑定，让力通过叶片顶端传递到叶根中心；载荷施加在叶根中心的加载点上，加载点节点坐标系转化到GL规定的叶根坐标系［12］；通过雨流技术法对时序载荷进行雨流计数，得到Mx、My、Mz、Fx、Fy、Fz这6 个载荷分量的波峰与波谷，将这12 个载荷作为疲劳单位工况载荷进行加载，3 个叶片分别施加叶根坐标系下的疲劳单位载荷，如图1 所示。

图1 整体计算模型

图2 变桨驱动与变桨轴承啮合模拟

图3 变桨轴承内外圈link10 连接模型

叶根载荷分量Mz通过变桨驱动与变桨轴承内圈的齿轮啮合传递，在有限元模型中，变桨驱动与变桨轴承齿轮啮合用beam4 伞单元进行模拟，并耦合啮合节点的周向自由度，如图2 所示；变桨轴承（双列四点接触球轴承）内圈与外圈采用实体建模，采用3D 杆单元link10单元（仅受压）模拟轴承滚子，轴承滚子刚度通过link10 单元的实常数进行赋予，螺母与轴承外圈绑定，如图3 所示。

轮毂的材料采用QT400，弹性模量为169 000 MPa；泊松比为0.275；变桨轴承材料采用42 CrMo，弹性模量为210 000 MPa；泊松比为0.3；主轴的材料采用QT500，弹性模量为170 000 MPa；泊松比为0.285。轮毂与变桨轴承和主轴的连接采用螺栓连接与绑定连接两种方式，用以分析两种建模方式对疲劳计算结果的影响。

1.1 螺栓连接模型

螺栓连接模型从叶片-变桨轴承-轮毂建到主轴，约束主轴端面；轮毂有限元模型按照实际的螺栓孔深度进行建模，螺栓长度按照螺纹啮合的长度进行建模；轮毂与变桨轴承和主轴之间均采用螺栓进行连接，用beam188 单元模拟螺栓，用PRETS179 单元模拟预紧力加载；叶片假体与轴承内圈、轮毂和变桨驱动、主轴与螺母、变桨轴承与螺母之间建立绑定接触；轮毂与轴承外圈、轮毂与主轴之间建立标准接触，如图4 所示。

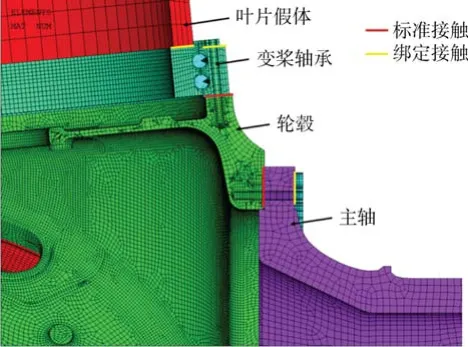
图4 螺栓连接模型

图5 绑定连接模型

1.2 绑定连接模型

绑定连接模型同样从叶片-变桨轴承-轮毂建到主轴，约束主轴端面；为了避免网格精度对计算结果影响，绑定连接的模型与螺栓连接的模型用相同的有限元模型；因此可以保证整体模型的网格与节点数量完全一致；模型直接的连接不建螺栓，完全靠绑定接触进行连接；叶片假体与与轴承内圈、轮毂和变桨驱动、主轴与螺母、变桨轴承与螺母之间建立绑定接触；轮毂与轴承外圈、轮毂与主轴之间同样建立绑定接触，如图5 所示。

2 疲劳损伤结果分析

2.1 疲劳计算方法与计算准则

疲劳计算采用应力幅值法（S-N 曲线法），该方法基于应力幅值（或称为应力范围）和循环次数（循环载荷次数）之间的关系，通过绘制S-N曲线来表达材料在不同应力水平下的疲劳强度和寿命。根据GL2010标准［12］绘制按照粗糙度、铸造等级和材料测试常数修正的S-N 曲线，如图6 所示［15］，并按照CriticalPlane 方法判断疲劳点。

根据Miner准则进行疲劳线性叠加，通过计算不同载荷条件下的载荷比并相加来评估总的累积损伤。式（1）为Miner疲劳计算的公式：

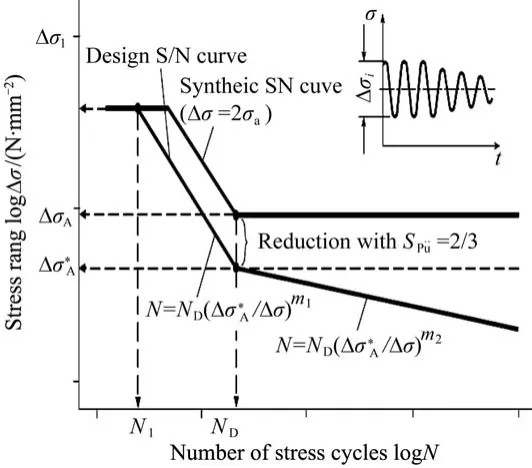
图6 疲劳计算S-N曲线

式中：D为总的累计损伤；i 为应力周期个数；ni为在应力幅值内的应力周期数；Ni为在应力幅值内可承受的应力周期数量。

将螺栓连接与绑定连接两种模型用相同的载荷进行疲劳计算，分别在两种仿真模型下，将各分量单位载荷的有限元结果与轮毂疲劳时序载荷进行组合，然后在进而计算出两种模型轮毂表面的疲劳热点及损伤值，对比两种模型疲劳损伤的分布与数值。按照轮毂疲劳损伤的分布，将疲劳损伤分为轮毂腹板面损伤与轮毂内部损伤两类进行对比分析。

2.2 轮毂腹板面疲劳结果对比分析

将轮毂按照上节所述的S-N曲线和疲劳计算方法进行疲劳计算，将计算结果进行整理，轮毂腹板上的疲劳损伤主要出现在开孔位置，并且两种计算模型的疲劳分布趋势较为一致；螺栓连接模型腹板面部分局部位置疲劳损伤如图7 所示，绑定连接模型腹板面对应位置部分局部位置疲劳损伤如图8 所示；将全部疲劳热点（损伤值大于或等于0.1）按从大到小汇总如表1 所示。

图8 绑定连接模型轮毂腹板面疲劳损伤云图

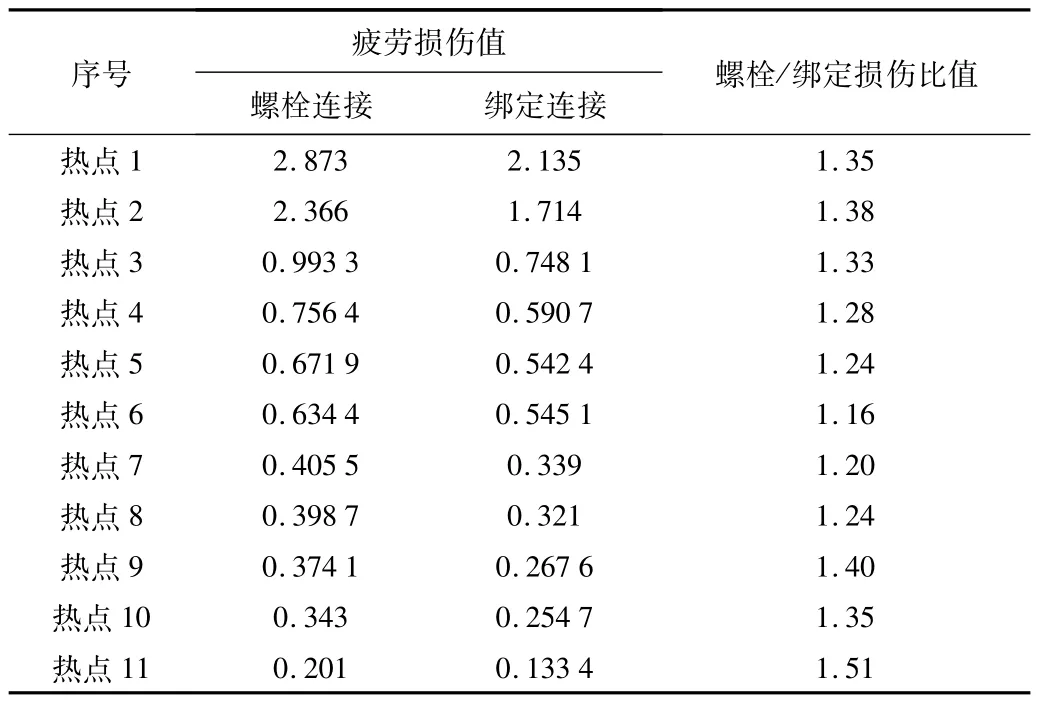
表1 轮毂腹板面疲劳热点汇总

由图7、图8 与表1 可以看出，由所列热点可以得到，螺栓连接腹板面的疲劳损伤值最大为2.873，最小热点疲劳损伤值为0.201，绑定连接腹板面的疲劳损伤值最大为1.35，最小热点疲劳损伤值为0.133 4，螺栓连接模型比绑定连接模型计算的疲劳损伤值整体偏大，疲劳损伤值最小的增大了1.16 倍，最大增大了1.51 倍，其余位置增大倍数在1.16 至1.51 倍之间。造成这种差别的原因主要是由于两种模型载荷的传递方式不同，绑定连接模型直接通过变桨轴承与轮毂的连接面传递载荷，并不能反映风力发电机叶片到轮毂真实的传力过程，螺栓连接直接通过螺栓进行载荷的传递，与实际较为符合；并且变桨轴承与轮毂绑定，间接增大了轮毂与变桨轴承连接法兰的刚度，导致绑定连接计算的轮毂腹板面疲劳损伤偏小。

对于整个轮毂腹板面来说，螺栓连接与绑定连接模型计算的轮毂腹板面疲劳损伤分布保持一致，疲劳损伤主要分布在工艺孔、驱动孔与中间大孔等开孔的位置与凸台圆角过渡处；说明对于腹板面来说，螺栓连接与绑定连接两种建模方式不影响疲劳损伤的分布趋势，螺栓连接与绑定连接计算的两个模型的疲劳损伤值的差别均在1.16～1.51 倍之间，说明在轮毂腹板面上，两种模型对于不同位置的疲劳损伤影响较为一致，并且对于腹板面来说，两种建模方式对于疲劳计算的影响不大。

2.3 轮毂内部疲劳结果对比分析

按照相同的粗糙度、铸造等级和材料测试常数为轮毂内部位置进行疲劳计算，螺栓连接模型轮毂内部疲劳损伤如图9 所示，绑定连接模型轮毂内部对应位置疲劳损伤如图10 所示；疲劳热点按从大到小汇总如表2 所示。由图9、图10与表2可以看出，螺栓连接和绑定连接两种模型在轮毂内部的损伤值比轮毂腹板面上相差的更大，由所列热点可以得到，螺栓连接轮毂内部的疲劳损伤值最大为5.269，最小热点值为0.58，绑定连接轮毂内部的疲劳损伤值最大为1.604，最小热点值为0.220 2，两种模型疲劳损伤差值最小相差2.63 倍，最大相差3.30倍。螺栓连接与绑定连接计算的轮毂内部的疲劳损伤分布也保持一致，疲劳损伤主要分布在轮毂中心处两腹板之间过渡圆弧处，由轮毂中心往轮毂前端与轮毂后端，疲劳损伤值递减；其主要原因是由于螺栓连接模型的传力位置引起，螺栓连接模型通过螺栓进行力的传递，螺栓传力的位置距离轮毂两腹板过渡圆弧的位置更近；绑定连接模型直接通过变桨轴承与轮毂的连接面传力，力的传递距离轮毂两腹板过渡圆弧的位置更远。

图9 螺栓连接模型轮毂内部疲劳损伤云图

表2 轮毂内部疲劳热点汇总

同时可以看出，对于轮毂内部的疲劳损伤，不同的位置疲劳损伤的比值差别更大，其主要是由于轮毂结构的影响，在轮毂中心处，两腹板在此位置距离最近，轮毂两腹板之间距离越近，越容易形成应力集中，并且对于应力集中的位置，对于载荷的变化更敏感，因此疲劳损伤在此位置会较大；由轮毂中心到轮毂前端与轮毂后端，两腹板距离越来越远，应力集中效应逐渐减弱，因此在这些位置轮毂疲劳损伤都较小。