主缆索股与鞍座间动态接触与微滑移机理研究

孙 远,王大刚,徐 伟,张德坤

(中国矿业大学 机电工程学院,江苏 徐州 221116)

大跨度多塔悬索桥由于具有跨越能力大、受力性能好及对地形适应能力强等优点，成为跨越千米以上障碍物最理想的桥型[1-3].作为悬索桥的主要承力构件，主缆以索塔、散索鞍支墩为支撑，锚固于两端锚碇[4-5].悬索桥服役期间，其自身恒载、风载和车辆通行引起的活载等多种载荷的耦合作用[6-8]产生的时变动载荷导致主缆索股与鞍座之间发生动态接触与微滑移，当主缆两侧的不平衡力超过主缆与鞍座间的极限摩擦力时主缆与鞍座之间将发生打滑现象[9-11]，进而造成悬索桥结构失稳甚至垮塌事故[12]，因此，针对主缆索股承受较大动载荷的典型工况开展悬索桥主缆索股与鞍座间的动态接触与微滑移机理研究，对保障大跨度多塔悬索桥的服役安全性具有重要意义.

国内外研究学者围绕悬索桥主缆与鞍座间的摩擦滑移问题已开展了大量的研究，学者们以Tokyo Port Link桥[13]、泰州长江大桥[14-16]、武汉鹦鹉洲长江大桥[17]和阳宝山特大桥[18]等多座服役中的悬索桥为工程背景，针对其主缆与鞍座间的摩擦滑移特性进行模型试验，全面模拟了各索股与索股之间、钢丝之间、索股与鞍槽间的真实接触特性，探究了主缆与鞍座间的摩擦系数的合理取值、抗滑移安全性评估以及滑移时刻判定等问题；高文丽等[19-21]针对主缆钢丝的动态接触与滑移行为开展了试验研究，运用原位观测手段揭示了主缆钢丝的动态接触与滑移特性及其受到接触滑移参数的影响规律；Wang等[22-23]和季申增等[24-26]基于ABAQUS、ANSYS等平台运用有限元仿真分析方法，采用简化的有限元模型研究了主缆索股、主缆钢丝的滑移特性.然而，目前已有的针对主缆索股与鞍座间摩擦滑移行为的仿真及试验研究均采用静态分级加载模式，模拟悬索桥实际服役环境中动载工况下的主缆索股与鞍座间动态接触与微滑移试验研究尚未见报道.本文作者以泰州长江大桥为工程实例设计试验平台并开展试验研究，揭示典型工况下悬索桥主缆索股与鞍座间动态接触与微滑移机理.

1 试验平台及试验参数

1.1 试验平台

泰州长江大桥采用PPWS法主缆，每根主缆包含的索股数量为169，每根索股由91根镀锌的高强度钢丝编制而成，钢丝半径为2.6 mm，索股钢丝与鞍槽之间的摩擦系数为0.2.主缆索股的截面为六边形，其在鞍座内的排列形式如图1所示.

Fig.1 Arrangement of the main cable strands in the saddle图1 主缆索股在鞍座内的排列形式

为模拟动态载荷工况下主缆索股与鞍座间的接触，依据实桥模型结构设计搭建主缆索股与鞍座动态接触与微滑移试验平台(图2)，该试验平台由基架单元、加载单元、鞍座、索股以及信号采集单元等组成.鞍座包角为48°，半径为1 m.试验索股采用37根直径为1.4 mm、抗拉强度为1 670 MPa的热镀锌钢丝进行编排，通过增加2根填充丝将鞍座内索股的断面整理为与鞍槽对应的矩形截面[图2(c)]，其截面尺寸为8.4 mm×8.67 mm.索股的中间区段放置在鞍座内的鞍槽上，两端分别穿过推板、调节螺栓、索力传感器和垫片，通过锚具进行固定，运用调节螺栓和穿心式索力传感器使各索股初始受力状态一致.试验时依据“索股两端同步张拉至恒载后一端固定，一端施加动态载荷”的加载模式，控制液压缸对索股施加预紧力及交变载荷[图2(d)]；运用接触压力传感器检测鞍座端部的接触压力；运用轮辐式压力传感器检测索股两端的张力；运用高速工业相机和相应的追踪程序通过鞍座上的缺口对索股与鞍座的接触界面进行视频拍摄并获得所标记参考点的位移信息.

Fig.2 Test platform for dynamic contact and microslip between main cable strand and saddle图2 主缆索股与鞍座动态接触与微滑移试验平台

1.2 试验参数

由于试验模型为缩比模型，故需要依据试验模型与实桥的主缆索股对鞍座的平均挤压接触应力基本一致的原则确定试验中对索股施加的预紧力值.图3所示为对索股两端施加预紧力后鞍座的受力示意图，沿鞍座的圆弧取一长度为dl、包角为dα的微段，则该微段上索股对鞍座的平均挤压接触应力为

Fig.3 Saddle force diagram图3 鞍座受力示意图

式中：F为对索股施加的预紧力，n为索股数，b为索股与鞍座底面(鞍槽)接触面宽度；r为鞍座半径.

基于已有的模拟实桥主缆索股的仿真研究采用的模型数据进行计算，单根索股对应的仿真参数为F=460 kN，n=1，b=46.8 mm，r=1.5 m，则索股对鞍座的平均挤压接触应力为

试验模型中索股截面长度为8.4 mm，即索股与鞍槽接触面宽度为8.4 mm，鞍座半径为1 m，综合考虑试验可操作性、试验装置加载能力等因素，采用4根索股进行试验[索股排列见图2(c)]，则施加的预紧力应为

为了模拟实际服役过程中的悬索桥主缆承受较大动载时发生完全滑动的极端工况，试验中施加的动态交变载荷应能够使主缆索股发生明显滑移，因此基于以上已确定的预紧力值，参考已有的加载方式为静态分级加载的主缆索股与鞍座摩擦滑移试验研究成果，确定交变载荷幅值为60kN.

结合试验装置的加载能力，确定典型工况条件下的试验参数列于表1中.

表1 试验参数Table 1 Test parameters

2 索股滑移

根据鞍座上缺口位置的不同将3个缺口分别称作固定端缺口、中部缺口和加载端缺口(图4).通过3个缺口对主缆索股的滑移特性进行探究.

Fig.4 Gaps of the saddle图4 鞍座缺口

2.1 同一接触位置下不同索股的滑移特性

控制高速工业相机通过加载端缺口对主缆索股与鞍座的接触界面进行视频拍摄，获得索股S1、S2和S3的滑移信息[如图2(c)所示，由于索股S2与S4对称布置在鞍座内，且边界条件相同，故只需选择其中1根索股作为研究对象]，探究主缆索股与鞍座同一接触位置处不同索股的滑移特性.

图5所示为循环周次为600次时单个加载周期内高速工业相机拍摄的视频中0.0、0.5、1.0、1.5和2.0s等5个时刻的截图，黄线为索股S1、S2和S3上所标记红点相应时刻的运动轨迹.

Fig.5 Video capture taken by the high-speed industrial camera图5 高速工业相机拍摄视频截图

运用追踪程序获得各标记点的滑移信息.由图6不同索股滑移曲线可知，3根索股滑移曲线的变化趋势总体上一致，初始阶段3根索股的滑移距离的增长速率基本一致.随着加载力的增大，各个索股滑移距离的增长速率大小关系为索股S3>索股S2>索股S1，且索股S1滑移距离的增长速率明显低于索股S2和S3.当加载力达到峰值即1s时，3根索股的滑移距离均达到最大值，大小关系为索股S3>索股S2>索股S1，且索股S1的最大滑移距离明显小于索股S2、S3.这是由于在鞍座内3根索股所处的位置不同，其接触关系也不同.如图7所示，索股S1底部与鞍槽接触，两侧与隔板接触，顶部与索股S2接触，与索股S2、S3相比，处于内层的索股S1受到了索股S3施加的外侧径向力的作用，其承受的总径向力明显大于处于外层的索股S2、S3，因此索股S1受到的抗滑摩擦力更大，导致其最大滑移距离最小.索股S2、S3顶部均不与其他物体接触，不承受外侧径向力的作用，与索股S1相比在受到加载力作用时更易发生滑移，索股S2两侧分别与外侧挡板和隔板接触，索股S3两侧与隔板接触，由于试验平台中隔板和外侧挡板的材料相同，故可认为索股S2、S3两侧的接触关系相同，但索股S2的底部与鞍槽接触，而索股S3的底部与索股S1接触，已有的研究成果表明，索股与索股间的摩擦系数小于索股与鞍槽之间的摩擦系数，因此索股S3受到的抗滑摩擦力小于索股S2，导致索股S3的最大滑移距离最大.

Fig.6 Slip curves of cable strands图6 索股滑移曲线

Fig.7 Contact relationship of cable strands图7 索股接触关系

进一步运用摩擦力-滑移距离滞后回线探究不同索股与鞍座间的接触状态，滞后回线的形状与接触状态的对应关系为直线-黏着状态、椭圆形-部分滑动状态以及平行四边形-完全滑动状态[27].通过计算测得的索股两端的拉力之差从而得到循环周次为600次时单个加载周期中索股不同时刻承受的摩擦力，同时结合各个索股的滑移距离数据得到不同索股的摩擦力-滑移距离滞后回线、索股与鞍座接触过程中的耗散能和索股的微滑移幅值(图8).由图8(a)可知，索股S2、S3的摩擦力-滑移距离滞后回线形状均为平行四边形，索股与鞍座间的接触面均为完全滑动状态，索股S3滞后回线呈现出的平行四边形的底边与索股S2相比更接近水平状态，这表明索股S3与鞍座间完全滑动状态的程度更高；与索股S2、S3相比，索股S1的摩擦力-滑移距离滞后回线呈接近平行四边形的椭圆形，索股与鞍座间的接触状态为接近完全滑动状态的部分滑动状态.以上研究结果表明，主缆索股承受动态载荷时各个索股个体与鞍座间的接触状态存在差异，当主缆索股整体承受较大动载时，与内层索股相比，外层索股与鞍座之间更容易发生完全滑动，索股间产生了分层滑移现象.

Fig.8 Hysteresis loops,dissipated energies and microslip amplitudes of different cable strands at the same contact position图8 同一接触位置下不同索股的滞后回线、接触过程耗散能及微滑移幅值

摩擦力-滑移距离滞后回线的面积可用于表征索股与鞍座接触过程中接触面材料损耗所需的耗散能[28].由图8(b)可知，索股S1、S2和S3与鞍座接触过程中材料损耗所需的耗散能分别为8.382、9.620和9.372J，这表明索股S2与鞍座间接触材料的损伤程度最高，索股S3次之，索股S1最小；由图8(c)可知，索股S1、S2和S3的滑移幅度依次增大.

2.2 不同接触位置下索股的滑移特性

控制高速工业相机分别通过固定端、中部和加载端3个缺口对索股S2与鞍座的接触界面进行视频拍摄，获得索股S2的滑移信息，探究单一索股与鞍座不同接触位置下的滑移特性.

图9所示为不同接触位置下的索股摩擦力-滑移距离滞后回线、索股与鞍座接触过程中的耗散能和索股的微滑移幅值.由图9(a)可知，不同接触位置处索股S2的摩擦力-滑移距离滞后回线形状均为平行四边形，固定端、中部和加载端等3个接触位置的索股S2与鞍座间的接触面均为完全滑动状态，说明索股S2与鞍座间的接触面整体均处于完全滑动状态.由图9(b)可知，索股S2在固定端、中部、加载端等接触位置与鞍座接触过程中材料损耗所需的耗散能分别为4.873、7.203和9.620J，说明从固定端到加载端不同接触位置的耗散能逐渐增大，索股与鞍座间不同接触位置材料的损伤程度从固定端到加载端逐渐增大.由图9(c)可知，索股不同接触位置的滑移幅度从固定端到加载端逐渐增大，且增长速率呈逐渐增大的变化趋势.

Fig.9 Hysteresis loops,dissipated energies and microslip amplitudes of cable strand at different contact positions图9 不同接触位置下索股的滞后回线、接触过程耗散能及微滑移幅值

3 摩擦系数

由于主缆索股与鞍座的接触面为圆弧面，故可以基于弧面法，根据挠性体摩擦的欧拉公式(2)计算主缆索股与鞍座间的摩擦系数[29-31].

式中：F1为重载端张力；F2为轻载端张力(F1>F2)；e为自然对数的底；μ为摩擦系数；α为索股与鞍座间包角，单位为rad.

对式(2)进行变换可得

取索股加载端张力为T1，固定端张力为T2，由于T1和T2的大小关系不一定，故代入式(3)后可得到索股与鞍座间摩擦系数的计算表达式

依据式(4)计算得到各个时刻的摩擦系数(包角α按48°换算，即0.837 8 rad)，将单个周期中大于0.85倍峰值的数据取平均值作为该周期的摩擦系数，根据各个周期的摩擦系数获得的摩擦系数的演化曲线，当演化曲线趋于稳定时取该阶段各周期摩擦系数的平均值作为索股与鞍座间接触稳定阶段的平均摩擦系数.基于以上计算理论及方法对测得的索股两端张力数据进行处理获取摩擦系数.

将4根索股作为整体，获得索股整体与鞍座间的摩擦系数演化曲线，如图10所示.由图10可知，试验初期摩擦系数由较小值快速增大，之后小幅波动并基本保持稳定，这是由于索股钢丝表面附着了油污和氧化膜，在摩擦过程中产生了一定的减磨作用，使得试验初期的摩擦系数较小.随后索股与鞍座间的持续动态接触导致索股钢丝表面的油污被磨掉、氧化膜破裂，索股钢丝材料基体与鞍座之间直接发生接触，索股与鞍座表面较大的微观凸峰被磨掉，更多较小的微观凸峰加入到摩擦过程中，索股与鞍座接触面的粗糙度增大，导致摩擦系数快速增大.随着循环周次的继续增大，索股与鞍座接触面材料剥落形成的磨屑也参与到摩擦过程中，摩擦系数处于小幅波动状态，随着摩擦过程的进行产生的磨屑被持续挤压而发生碎化和氧化并不断溢出，当索股与鞍座接触面磨屑的产生和溢出速率基本相同时，摩擦系数基本保持稳定.索股整体与鞍座接触稳定阶段的平均摩擦系数为0.310.

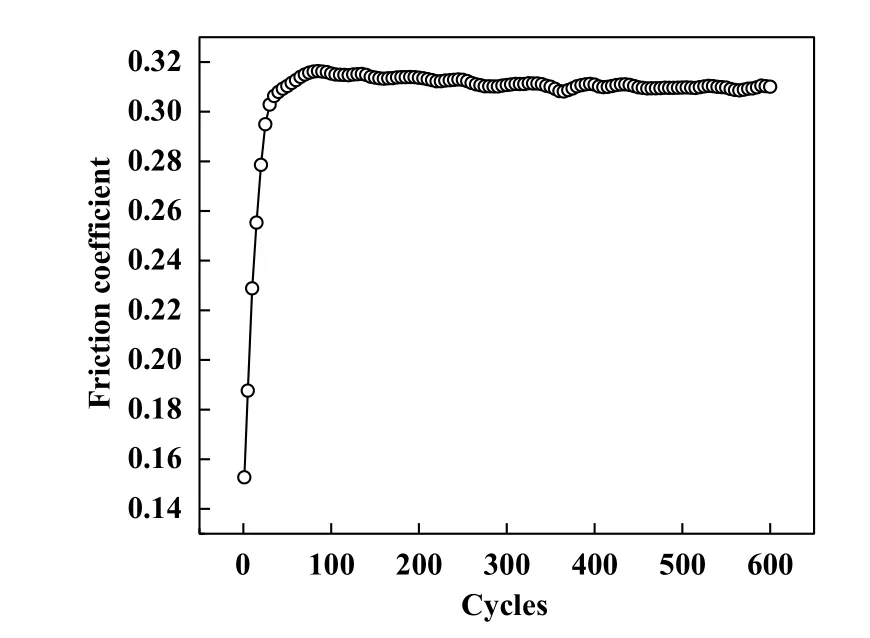
Fig.10 Evolution curve of friction coefficient图10 摩擦系数演化曲线

进一步对索股S1、S2和S3个体的摩擦系数进行探究.由于索股S1、S2和S3的接触关系不同，如图2(c)所示，鞍槽与隔板均为鞍座的一部分，则索股S1、S3的摩擦副包括索股-索股、索股-鞍座，索股S2的摩擦副为索股-鞍座，为避免与摩擦系数的定义产生歧义并便于表征，将根据式(4)获得的各索股的摩擦系数称作名义摩擦系数.

图11所示为不同索股的名义摩擦系数演化曲线及稳定阶段的平均名义摩擦系数，由图11(a)可知，不同索股的名义摩擦系数的变化趋势相似，与索股整体与鞍座间的摩擦系数演化曲线一致，均为试验初期由较低值快速增大，之后基本保持稳定.由图11(b)可知，索股S1、S2、S3稳定阶段的平均名义摩擦系数分别为0.336、0.311、0.279，即索股S1>索股S2>索股S3.

Fig.11 Nominal friction coefficient of different cable strands图11 不同索股的名义摩擦系数

依据对称结构关系可认为索股S4的名义摩擦系数与索股S2相同，则4根索股的稳定阶段平均名义摩擦系数的平均值为

可知索股个体稳定阶段平均摩擦系数的平均值与4根索股整体与鞍座间接触稳定阶段的平均摩擦系数一致，说明以名义摩擦系数表征索股个体的摩擦水平具备可靠性.

4 端部接触压力

图12所示为循环周次为600次时单个加载周期中鞍座固定端与加载端接触压力的变化曲线，由图12可知，加载端接触压力的变化趋势与加载施加的交变载荷[图2(d)]基本一致，变化范围为11.21～17.23 kN，而固定端接触压力的变化呈现出滞后性，初始阶段缓慢增大，随后曲线斜率陡增，快速增大到峰值后缓慢减小，之后又快速降低至谷值，其变化范围为12.69～14.27 kN，这是由于鞍座接触压力来源于索股施加的径向力，而索股产生的径向力的大小是由索股的张力大小决定的，鞍座两端的接触压力受到鞍座两侧索股张力的影响，试验中加载端一侧索股的张力变化趋势与试验中施加的加载力的变化趋势基本一致，因此加载端接触压力呈上述变化规律；由于索股与鞍座间摩擦力的平衡作用，固定端一侧索股的最大张力小于加载端一侧索股，索股与鞍座接触稳定后固定端一侧索股张力的变化范围在加载端一侧索股张力的变化范围之内，因此固定端接触压力的变化范围在加载端接触压力的变化范围之内.

Fig.12 Contact pressure at the saddle end图12 鞍座端部接触压力

为进一步探究加载力对鞍座端部接触压力的影响并便于对比固定端与加载端接触压力受加载力影响的差异，将固定端与加载端0～1 s各个时刻的接触压力减去其各自0 s时的接触压力得到接触压力增量，将0～1 s各个时刻的加载力减去0 s时的加载力即预紧力得到加载力增量，获得加载力由谷值增至峰值区段中鞍座端部接触压力增量与加载力增量间的关系图，如图13所示.由图13可知，随着加载力增量的增大，加载端接触压力增量呈线性增大趋势，而固定端接触压力增量呈先几乎不变，然后缓慢增大的变化趋势，这是由于加载力增量较小时，加载力增量几乎被索股与鞍座间的摩擦力完全抵消，固定端一侧索股的张力基本不变，随着加载力增量的增大，摩擦力逐渐不足以平衡加载力增量，固定端一侧索股的张力逐渐增大，固定端接触压力也随之增大.固定端与加载端的最大接触压力增量分别为1.58 kN、6.02 kN.

Fig.13 Relationship between incremental contact pressure and incremental loading force at saddle end图13 鞍座端部接触压力增量与加载力增量间的关系

5 结论

a.主缆各索股承受动态载荷时不同索股个体与鞍座间的接触状态存在差异性.当主缆索股整体承受较大动载时，主缆索股与鞍座同一接触位置处，外层索股与鞍座间更容易发生完全滑动，索股间产生分层滑移，不同索股的微滑移幅值由内层到外层依次增大.

b.索股整体与鞍座间的摩擦系数呈快速增大-小幅波动并逐渐稳定的变化趋势，且接触稳定阶段的平均摩擦系数为0.310.索股S1、S2、S3稳定阶段的平均名义摩擦系数的大小关系为索股S1>索股S2>索股S3，且4根索股稳定阶段平均名义摩擦系数的平均值与索股整体与鞍座间接触稳定阶段的平均摩擦系数一致，名义摩擦系数表明索股个体的摩擦水平具备一定的可靠性.

c.随着加载端力增大，固定端接触压力呈现小幅波动(或稳定不变)-缓慢增大的变化趋势，加载端接触压力增量呈线性增大趋势.鞍座固定端和加载端接触压力的变化范围分别为12.69～14.27 kN和11.21～17.23 kN，固定端接触压力呈缓慢增大-快速增大-缓慢减小-快速减小的变化趋势，加载端接触压力与交变载荷的变化趋势基本一致.