基于粗糙集理论的混凝土拱桥加固或拆除方案综合判定

张胜林,周水兴,耿川雁,叶 航,刘 彬

(1. 贵州省公路工程集团有限公司,贵州 贵阳 550003;2. 重庆交通大学 土木工程学院, 重庆 400074;3. 贵州桥梁建设集团有限责任公司,贵州 贵阳 550015)

20世纪60年代至90年代,国内建造了数量众多的双曲拱桥和桁式组合拱桥,但在多年使用中出现病害严重、技术状况差、技术等级偏低等系列问题,不少拱桥进行了加固改造或拆除重建。当前,针对混凝土拱桥加固或拆除决策主要基于桥梁技术状况和专家评定,决策因素相对单一。层次分析法和模糊理论在资源分配、生产决策、信息系统、环境评价等方面得到广泛应用,但存在指标权重求解过程繁琐,无法对指标体系中的各指标进行定权和变权的问题[1-3]。粗糙集理论在信息获取、人工智能、安全评价、决策分析等领域应用广泛,是解决模糊关系和不确定性问题的数学工具,将粗糙集理论应用于混凝土拱桥加固或拆除决策中[4-6],具有以下优点:充分利用专家理论和经验知识,指导决策实践;有效处理信息以及信息间的不确定性,提高决策水平;有效改善数据间的冗余关系、依赖关系,简化指标体系;合理确定指标权重,克服主观性问题;提高对决策问题的处理能力和计算方法。

笔者基于粗糙集理论,建立混凝土拱桥加固或拆除方案综合判定模型,将其应用于贵州省花鱼洞大桥的加固或拆除方案评定中,验证了综合判定模型的可行性。

1 综合评判指标体系建立

混凝土拱桥加固或拆除判定,涉及到技术状况、社会发展、国家方针、政府行为、社会资源、寿命成本等诸多方面,遵循“科学性、综合性、稳定性、可比性、可行性、系统性”的评判原则,将混凝土拱桥加固或拆除综合评判指标归结“技术类”、“社会类”、“经济类”3类中间层指标,22个底层评判指标,如图1。

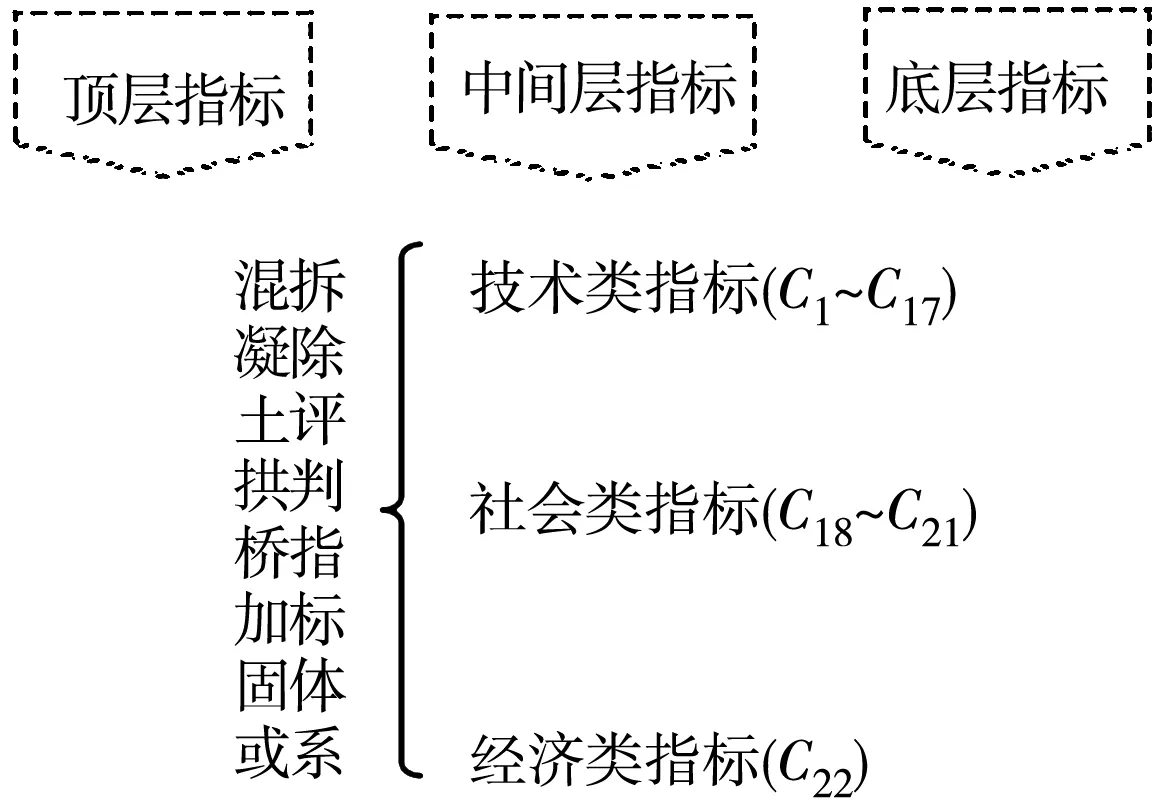
图1 混凝土拱桥加固/拆除评判指标体系Fig. 1 Reinforcement / demolition evaluation index system of concrete arch bridge

技术类指标即C1～C17,其中C1～C6(下部结构)为:基础位移、冲刷程度、材料老化、墩台裂缝、墩台位移、墩台承载力;C7～C14(上部结构)为:拱圈线形、主拱圈承载力状况、主拱圈裂缝情况、材料老化、横系梁(横隔板)开裂、桥道梁(腹孔)承载力、桥道梁裂缝、其它构件缺损程度;C15～C17为(桥面系):桥面铺装损伤程度、伸缩缝与支座损伤程度、栏杆与照明受损状况。

社会类指标即C18～C21:桥面通行能力、桥下通航能力、社会影响、碳排放量。

经济类指标即C22:加固与重建寿命周期内费用效益模型。

图1中因技术类指标、社会类指标、经济类指标是从结构自身状态、结构对当地社会和经济发展的影响、结构加固和重建费用效益比选3个不同方面来综合反映拱桥的加固或拆除,三者相辅相成,但技术类指标对社会类指标和经济类指标均有导向性作用,故确定中间层指标的权重为:

技术类∶社会类∶经济类=2∶1∶1。

2 决策方案的综合判定

2.1 基于粗糙集理论的综合评判方法

采用粗糙集理论进行混凝土拱桥加固或拆除综合评判的主要步骤如下:

1)从“技术、社会、经济”3个维度,构建混凝土拱桥加固或拆除综合评判指标体系。

2)建立评判指标表,确定混凝土拱桥加固或拆除综合评判各底层指标评判标准。

3)结合专家评价法,应用粗糙集理论中基于差别矩阵的属性约简算法对指标体系进行属性约简,根据知识的依赖性计算约简后的指标重要度并赋权,对约简后的指标体系进行综合判定计算,据此得出混凝土拱桥是加固或拆除重建的判定结果。

2.2 建立评判指标表

针对拱桥的加固与拆除决策进行研究,桥梁结构状态相对较差,依据拱桥病害程度,基于粗糙集理论的离散处理方法,使用“1、2、3”分别代表指标等级,对应于“良(加固)、中(部分拆除改造)、差(拆除重建)”3个等级,得到直接明了的判定结果。专家仅需按照3个等级对拱桥的各项指标进行打分评判,形成表1的混凝土拱桥加固或拆除综合判定评判指标。

表1 混凝土拱桥加固或拆除综合判定评判指标

表1中,U={x1,x2,x3,…,xm-1,xm}为论域,表示有m位专家参与了评判;cij表示第i位专家对第j个条件属性的判定值,cij={1,2,3}={良,中,差};由于专家对单项指标的评判不能代表其对整体方案的评判结果,因此还需给出第i位专家基于各项条件属性判定结果给出的指标体系总体决策结果di,di={1,2,3}={良,中,差}。

2.3 建立判定模型

2.3.1 基于差别矩阵的属性约简算法

由于指标体系涵盖的指标较多,不同建设方案所对应的代表性指标也不相同,然而代表性指标又影响判定结果,因此需要根据表1中的方案判定指标,利用粗糙集理论中的差别矩阵约简算法进行约简[7-11],具体步骤如下:

1)统计表1中判定结果不同项所组成的集合lij(i,j=1,2,…,m),建立基础差别矩阵L;从中找出最简集合项,即为核指标B。

2)利用核指标对基础差别矩阵进行约简,求解新的差别矩阵。若B∩lij≠∅,需将lij置为∅,即去除基础差别矩阵中含有核指标的集合。

3)将新差别矩阵中出现的高频指标与核指标共同组成约简后的最终指标体系[5]。

2.3.2 判定指标权重的分析及确定

基于属性依赖度,计算各指标的重要度Pi:

Pi=γC(D)-γC-{Ci}(D)

(1)

式中:γC(D)为决策属性D对条件属性C的依赖度;γC-{Ci}(D)为决策属性D对去除Ci属性后的条件属性C-{Ci}的依赖度。

2.3.3 建立综合判定体系

开展混凝土拱桥加固或拆除综合判定时,将评价集E分为3个等级:

E={e1,e2,e3}={良,中,差}

(2)

对应于评价等级,需将最终约简指标体系中的指标进行分类,以构成模糊判定矩阵V:

(3)

其中,vni=K/m表示在约简指标体系中第n个指标评分为ei(良、中、差)的人数K占专家总人数m之比。

将最终约简指标体系中的指标权重与判定模糊矩阵相乘,得到评价向量Y,如式(4):

(4)

评价向量Y中包含y1、y2、y3共3个元素,其含义分别代表判定结果为“良”、“中”、“差”的概率。按照最大隶属度原则,三者中的最大者即为最终判定结果。

3 工程实例

3.1 工程概况

花鱼洞大桥位于贵州省国道G320清镇境内,桥梁全长290 m,主跨为150 m预应力混凝土桁式组合拱桥,1993年建成通车。运营13年后,因严重病害进行维修加固,加固后运营至2016年拆除重建。

3.2 加固或拆除判定指标体系建立

从行业主管部门、设计、施工、管养、科研等单位,邀请10位专家对花鱼洞大桥进行指标等级判定,得到表2的评判指标结果。

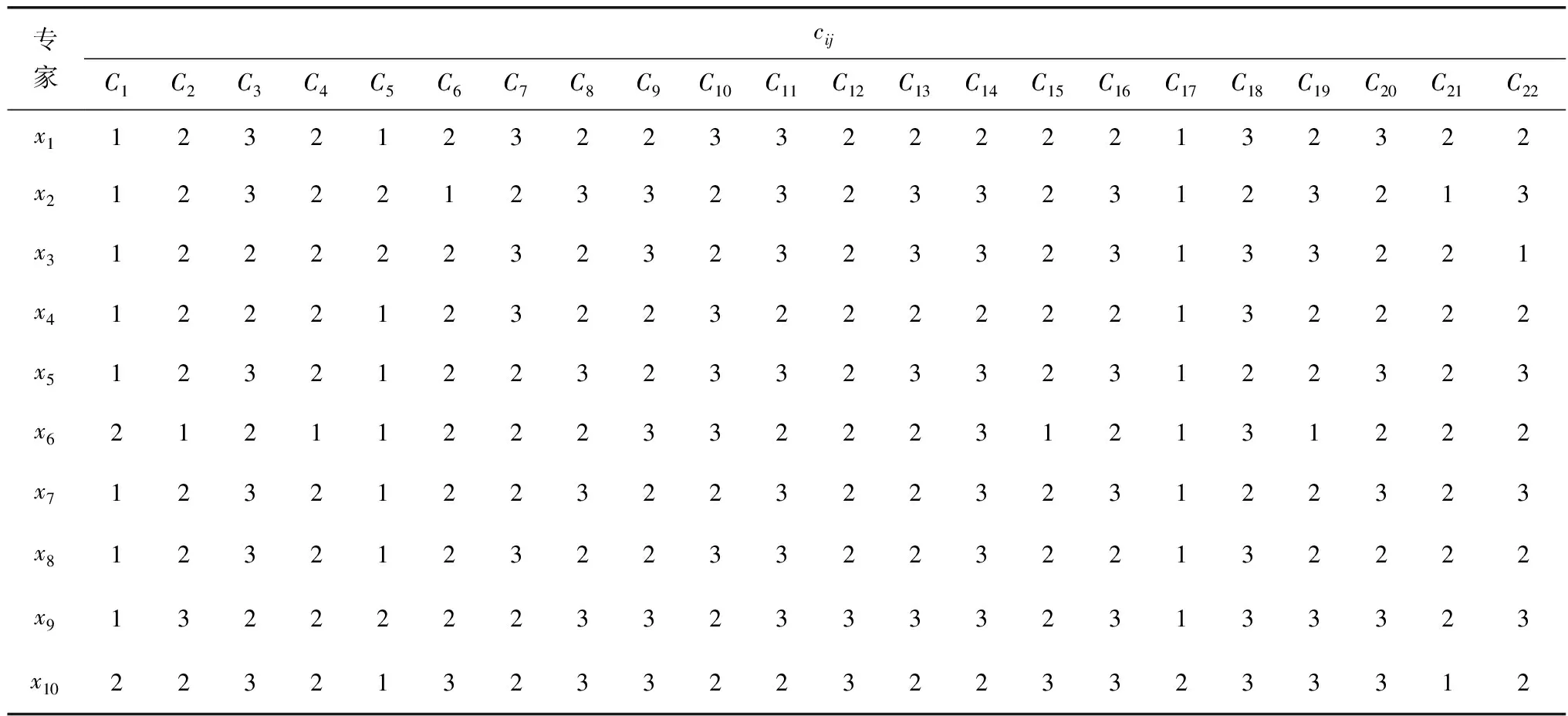
表2 花鱼洞大桥加固或拆除评判指标

基于差别矩阵的属性约简算法,将表2中任意2位专家判定结果不同的指标项进行集合,作为基础差别矩阵L的一个元素,填入基础差别矩阵的对应位置。以专家x1和x2的评价结果为例,C1列中2位专家的判定结果均为1,故该项不予计入,C5列中的判定结果分别为1和2,需要计入。同理可得到其他列的判定结果,最终得到C5、C6、C7、C8、C9、C10、C13、C14、C16、C18、C19、C20、C21、C22等14个指标项,所构成的集合l21填入表3中x2行/x1列。类似地可得到其他元素。由于专家自身的意见不会相悖,因此差别矩阵为下三角矩阵。限于篇幅,文中仅给出了部分元素。

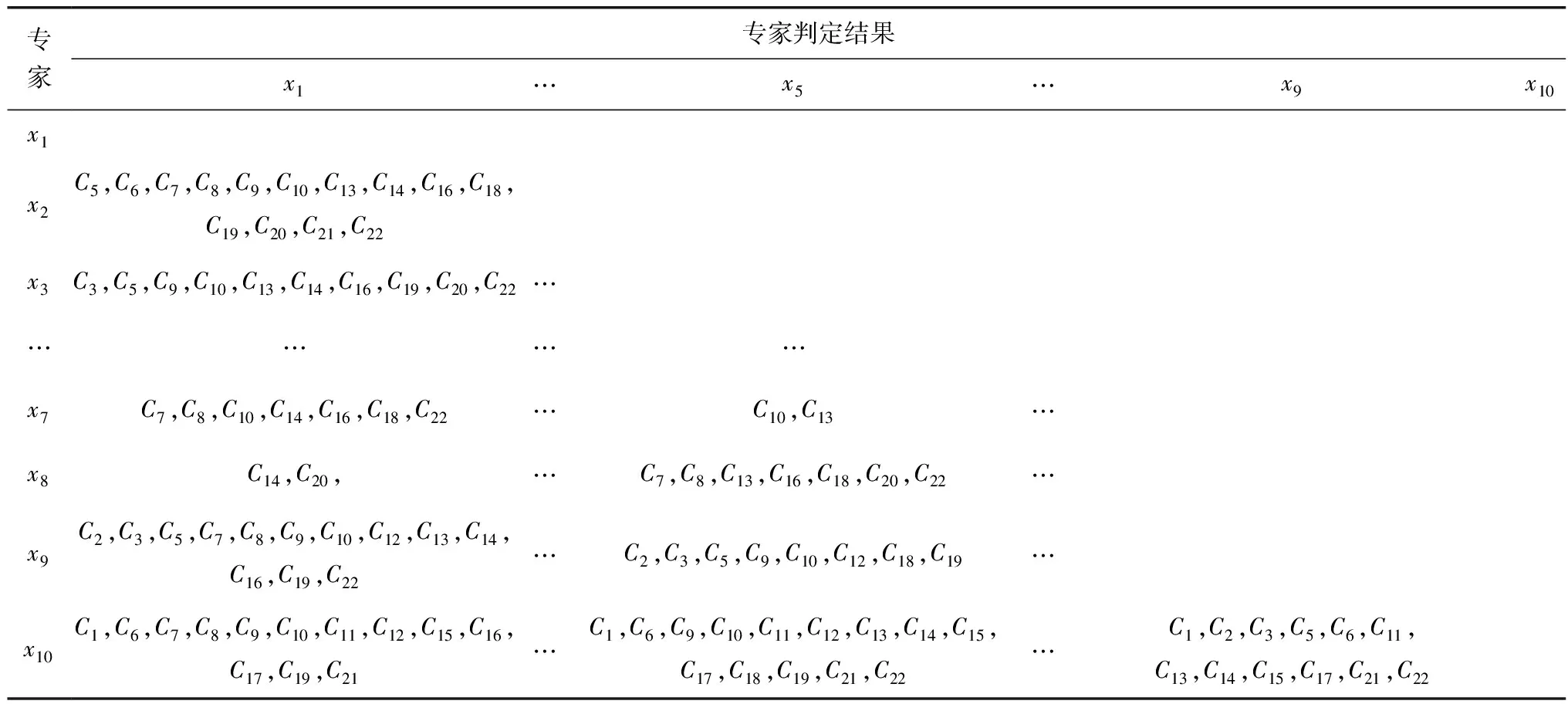
表3 加固或拆除基础差别矩阵L

由表3可以看出{C10,C13}和{C14,C20}构成了最简集合项,根据粗糙集理论中核的定义,该组合项即为核指标B。得到核指标后,在基础差别矩阵中去除包含有核指标的元素后,构成了新的差别矩阵,同时将新差别矩阵中的高频指标C3、C7、C8、C9、C16、C18、C19、C22,再与核指标C10、C13、C14、C20共同组成最终的约简指标体系C′:

C′={C3,C7,C8,C9,C10,C13,C14,C16,C18,

C19,C20,C22}

(5)

3.3 指标体系权重计算

笔者在技术类和社会类指标中采用约简算法,经济类指标中采用公式决策法[12],因此,按照中间层分类进行分项决策。

以技术类指标为例,该中间层中C1、C2、C4、C5、C6、C11、C12、C15、C17项被约简掉,剩余指标项与决策属性共同组成表4的决策表。

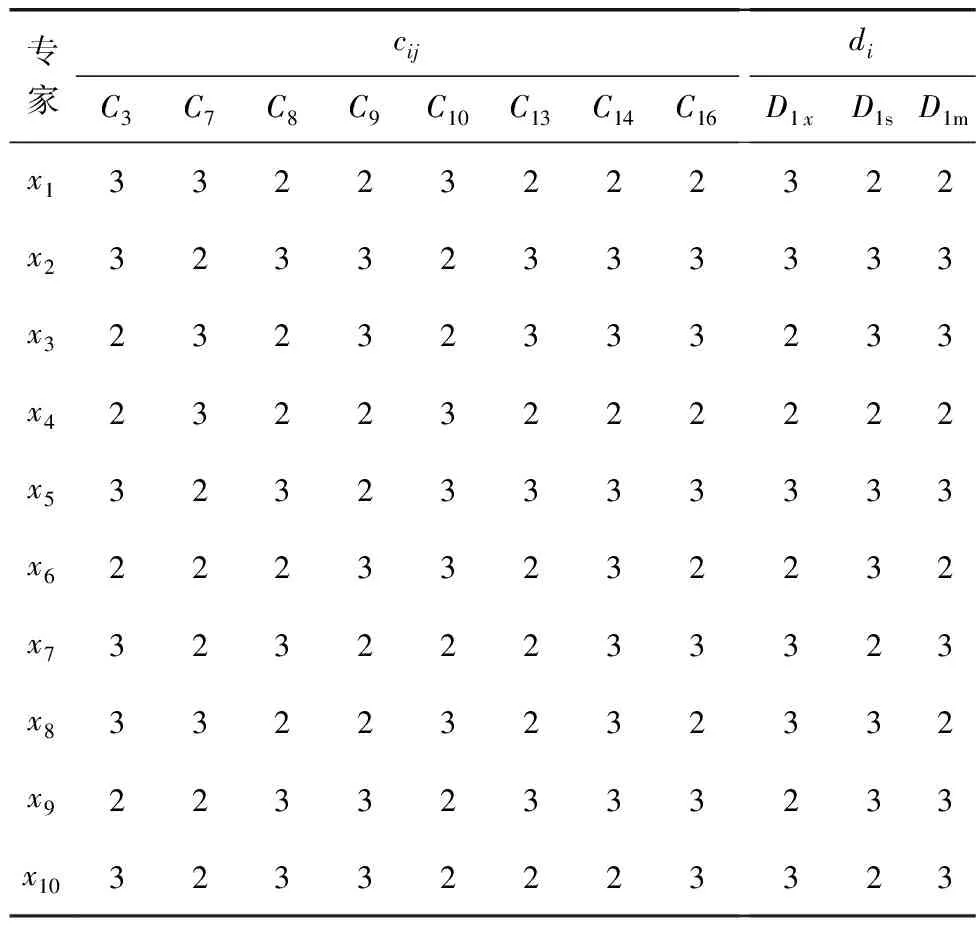
表4 技术层指标决策

计算决策属性集(下部结构D1x,上部结构D1s,桥面系D1m)的判定结果对条件属性集CH判定结果的依赖度γCH(D1x)、γCH(D1s)、γCH(D1m)的步骤如下:

I(D1x)={(x1,x2,x5,x7,x8,x10),(x3,x4,x6,x9)}

I(CHx)={(x1,x2,x5,x7,x8,x10),(x3,x4,x6,x9)}

I(D1s)={(x1,x4,x7,x10),(x2,x3,x5,x6,x8,x9)}

I(CHs)={(x1,x4),(x2,x9),x3,x5,x6,x7,x8,x10}

I(D1m)={(x1,x4,x6,x8),(x2,x3,x5,x7,x9,x10)}

I(CHm)={(x1,x4,x6,x8),(x2,x3,x5,x7,x9,x10)}

PCHx(D1x)={x1,x2,x3,x4,x5,x6x7,x8,x9,x10}

PCHs(D1s)={x3,x5,x6,x7,x8,x10}

PCHm(D1m)={x1,x2,x3,x4,x5,x6x7,x8,x9,x10}

式中:I(CHx)、I(CHs)、I(CHm)分别表示条件属性集CHx(下部结构)、CHs(上部结构)、CHm(桥面系)按判定结果得到的分类集合;I(D1x)、I(D1s)、I(D1m)分别表示决策属性D1x、D1s、D1m按照判定结果得到的分类集合;PCHx(D1x)、PCHs(D1s)、PCHm(D1m)分别对应属性集CHx、CHs、CHm的分类结果按决策属性集D1x、D1s、D1m得到的分类集合。

同理,可得到决策属性D1x、D1s、D1m的判定结果对去除Ci指标后的指标体系CHx-{Ci}、CHs-{Ci}、CHm-{Ci}的依赖度CHx-{Ci}、CHs-{Ci}、CHm-{Ci},(i=3,7,8,9,10,13,14,16),结果如表5。

表5 技术层各指标的γCHj-{Ci}(D1j)(j=x,s,m)

利用表5就可计算技术准则层各指标重要度,以C3指标重要度αCHD1(C3)为例:

αCHD1(C3)=γCHx(D1x)-γCHx-{C3}(D1x)=1-0=1

类似地可计算表4中其余项的指标重要度。

参照技术准则层,可得到社会层各项指标的重要度αCHD2(Ci)(i=18,19,20)。

以分项指标约简后的技术类各指标数量占技术类总指标数之比为系数ε1,同理社会类系数ε2,按式(6)、式(7)将重要度非零的指标权重进行归一化处理:

PCai=λaεaαCHDa(Ci)

(6)

式中:Ci为各层重要度非零指标,i=3,14,16,18,19,20;λa为中间层常权系数,a=1时为技术类指标常权系数λ1=2,a=2时为社会类指标常权系数λ2=1;εa为各层系数(a=1,2)。

归一化各指标权重为:

(7)

式中:wi为归一化后各指标权重,a=1,2,i=3,14,16,18,19,20。

由此得到表6所示的各指标权重。

表6 加固或拆除指标体系权重

根据表2分别计算表6中各指标项判定结果为“1”、“2”、“3”等级的人数与专家总人数的比值vne,构成模糊判定矩阵V:

结合表6,根据式(4),判定结果Y为:

Y1=(0 0.125 13 0.191 46)

Y2=(0.009 61 0.108 92 0.137 75)

式中:Y1为技术层判定结果;Y2为社会层判定结果。

根据最大隶属度原则,技术类指标与社会类指标判定等级均为y3,即判定结果为差,花鱼洞大桥从技术类角度和社会类角度出发建议拆除重建。

经济类指标采用公式决策法。现有3个方案,方案1为全桥加固方案,方案2为结构部分拆除加固方案,方案3为拆除重建方案。按2019年价格估算,数据如表7,已知基准收益率i0为10%,净现值N≥0,内部收益率R≥i0。

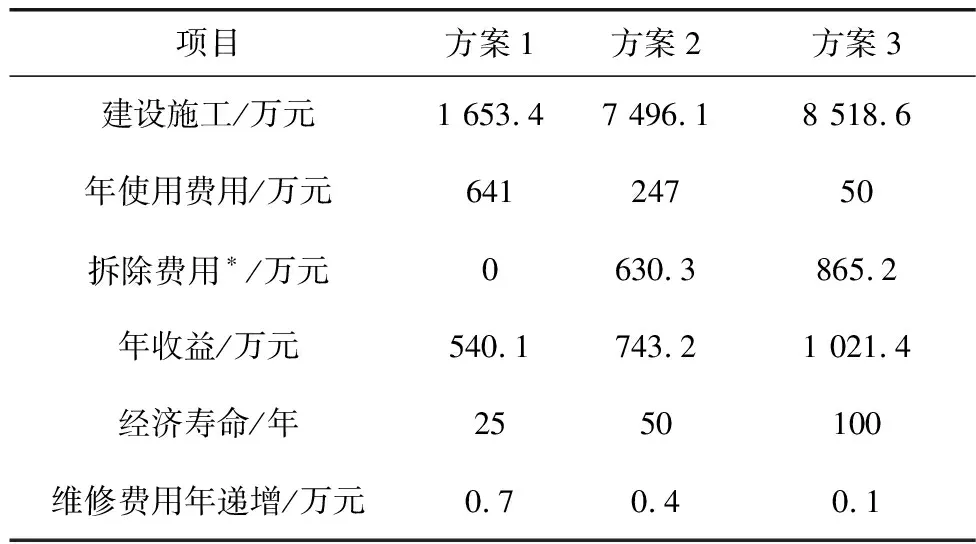
表7 三种方案费用、效益估算

如果将上述3个方案考虑成具有等额年效益,运用费用效益模型进行方案经济比选,ΔQ12为方案1与方案2的等额年效益差:

ΔQ12={743.2[P/A,10%,50]/[7 496.1+247(P/A,10%,50)+630.3+0.4(P/G,10%,50)]}-{540.1[P/A,10%,25]/[1 653.4+641(P/A,10%,25)+0.7(P/G,10%,25)]}<0

方案1较方案2的费用效益更优,故将方案3与方案1进行比选,ΔQ13为方案1与方案3的等额年效益差:

ΔQ13={1 021.4[P/A,10%,100]/[8 518.6+50(P/A,10%,100)+865.2+0.1(P/G,10%,100)]}-{540.1[P/A,10%,25]/[1 653.4+641(P/A,10%,25)+0.7(P/G,10%,25)]}>0

式中:P/A为年金现值系数;P/G为等差年金换算系数。

方案3较方案1的费用效益更优,即从经济类角度建议花鱼洞大桥拆除重建。

综合技术类、社会类、经济类3个评判结果,根据最大隶属度原则,建议花鱼洞大桥拆除重建。

4 结 语

笔者建立了混凝土拱桥加固或拆除方案综合判定模型,从技术、社会、经济3个方面给出了22个评判指标值,建立了评判指标体系,运用差别矩阵约简算法,得到了评价向量,将其应用于花鱼洞大桥加固或拆除方案综合判定中,最终判定为拆除重建,为建设单位科学决策提供了依据。

此外,建立的判定方法不仅适用于混凝土拱桥,还适用于早期的石拱桥或其他桥型,对此仅需根据桥型特点修改评判指标体系中与之相关的指标,然后按文中给出的评判模型、指标体系权重计算方法进行综合判定。