浮泥特性及输移规律综述

2023-11-13孟彩侠

重庆交通大学学报(自然科学版) 2023年10期

刘洁,周鹏,孟彩侠

(1. 重庆交通大学国家内河航道工程技术研究中心,重庆400074; 2. 重庆交通大学河海学院,重庆 400074)

河流所携带的泥沙在水库、河口、港池及海岸等地区落淤后,会与水流混合形成具有一定流动性的近底含沙悬浮体。20世纪50年代,C．C．INGLIS 等[1]在研究Thames河口的泥沙运动规律时,首次将近底高含沙水体称为浮泥(fluid mud),此后该名词逐渐为学界所接受,特指理化性质有别于一般低浓度含沙水体的近底细颗粒泥沙、有机物和水的混合体,是一种普遍存在于淤泥质沉积环境中的因悬沙落淤或土体液化起悬的中间产物[2]。

在我国,浮泥广泛存在于海湾(如辽东湾、渤海湾)、河口(如长江口、珠江口)、港口(如天津港、连云港、上海港、广州港等)及水库(如小浪底水库)中[3-4]。浮泥的存在给很多工程带来了实际问题,一方面是港池、航道骤淤问题非常严重,钳制了港口吞吐量增长,增加了港池航道疏浚维护成本;另一方面由于细颗粒泥沙能吸附污染物并能随水流输运,其排放会造成水环境的二次污染[5]。为解决浮泥在港池、航道的淤积问题,从20世纪50年代开始,一些学者便对浮泥成因、运动及监测开展了研究,且取得了一定成果,指导了工程发展[6-11]。笔者基于国内外学者的研究成果,对浮泥形成机制及观测方法,浮泥特性及输移规律进行了分类和总结,为工程实践提供理论依据。

1 浮泥形成及观测

1.1 浮泥形成

根据学者们形成的共识可知[12-14]:丰富的细颗粒泥沙来源和多样的外部水动力环境是形成浮泥的必要条件,根据浮泥形成过程不同可归纳为3种情况。第1种是在潮流、波浪及水流等动力产生的切应力大于细颗粒泥沙的临界起动应力时,泥沙颗粒起动悬扬,并随水流运移到航道或掩护区而落淤,黏性泥沙在沉降过程中,由于絮凝作用会逐渐形成絮团颗粒,当絮团颗粒浓度达到一定程度后会逐渐呈现蜂窝状的高含沙絮团结构,并且与靠近河床底部的上层水体间出现清晰界面,当浓度继续增大至流变特性发生改变时便形成了浮泥,如图1;第2种是海床表层淤泥软化后在水平方向发生流动后聚集在一起形成浮泥;第3种是具有一定坡度的海滩、航槽边坡或峡谷坡面上的泥沙在大风浪等作用下起动后形成高含沙水体,在重力作用下向坡脚运移汇聚而形成浮泥。一般而言,淤泥质海岸和河口地区浮泥较为常见,因为这些地区泥沙粒径小,泥沙容易悬浮和产生絮凝。李九发等[15]在研究长江河口浮泥形成机理及变化过程中指出:在长江口径潮流相互作用下存在一个咸淡水混合过渡带,此处大量泥沙汇聚,易促进细颗粒泥沙絮凝沉降,近河底常出现高浓度的浮泥层。

图1 浮泥形成过程Fig. 1 Formation process of fluid mud

浮泥特性与其密度具有十分密切的关系,大多数学者[6,13,16-17]一般采用密度或含沙量来区分浮泥(国内多采用密度区分,国外多采用含沙量区分)。当浮泥流动性明显消失时,流变性参数随浮泥重度增大而明显加大时的浮泥特性为浮泥上界;当含沙水体中泥沙在絮凝沉降过程中,底部泥浆与上部水体出现清晰界面,泥浆流型由牛顿体转为宾汉流体时的浮泥特性为浮泥下界。以浮泥密度来定义浮泥界限时,浮泥密度基本介于1 020～1 300 kg/m3。黄胜等[17]认为:浮泥密度上限为1 250 kg/m3,下限为1 030 kg/m3;李九发等[18]测得长江口浮泥密度介于1 040～1 250 kg/m3;李昆鹏等[19]在研究小浪底水库浮泥对后期异重流运行影响时,以1 250 kg/m3作为浮泥上限。

国外学者通常还采取另一种区分浮泥的方法,即以水体含沙量来定义浮泥界限。N．V．M．ODD等[8]认为:浮泥含沙浓度上限为1 200 kg/m3,下限为1 080 kg/m3;G．C．KINEKE等[20]将悬浮泥沙浓度400 kg/m3定义为浮泥层浓度上限,将10 kg/m3定义为浮泥层浓度下限;J．C.WINTERWERP等[21]将浮泥定义为含沙浓度在胶凝点以上,即介于10～100 kg/m3的黏性泥沙悬浮体。

1.2 浮泥观测

国内外针对浮泥观测已有较长历史,且观测方法较为多样,依据观测方法原理不同可分为4类[22]。第1类,以浮力原理进行某一重度的浮泥界面深度测量,如测深砣法。庞启秀[13]以三爪砣测深垂线采集了大量浮泥样本,确定了天津港适航淤泥重度为12.7 kN/m3。第2类,以射线穿透不同密度的物质衰减快慢不同原理来测量浮泥的密度值,如γ射线原理测量法。上海航道局自1976—2000年先后采用FE-101双频回声探测仪、浮泥分层取样器、高浓度γ射线测沙仪并结合CTD,发现长江口南槽有浮泥,而北槽未见浮泥[23]。第3类,以超声波反射或散射的原理测量浮泥密度或含沙量,如超声波原理测量法、音叉密度测量法。李九发等[18]在长江口利用Innerspace-449热敏式双频道回声探测仪测量了浮泥上下界面,并利用HSDM声学高密度测沙仪测量了浮泥的密度值。第4类,基于超声波、射线或浮力原理融合而形成的观测系统,如耦合测量法。许宝华等[24]采用SILAS走航式水底浮泥连续密度测量系统,对象山港航道淤泥回淤厚度进行了观测,其观测结果有较高的精确度。A．S．OGSTON等[25]和R．P．HALE等[26]分别采用搭载光学后向散射传感器OBS观测系统,在加利福尼亚北部陆架观测到了浮泥层形成并以重力流形式向海运动的过程。近年来,也出现了新的浮泥观测方法,如栾红等[27]利用Iandsat8系列高分遥感卫星资料对珠江口悬沙进行了四季遥感反演和分析,得到了珠江口海域悬浮泥沙各季节的典型分布特征。

上述技术具有不同的优缺点:测深砣测量法费时费力,测量精度受人为操作影响大;γ射线测量法分辨率高且直观,不易受到外界因素干扰,但测量时速度较超声波测量慢;超声波测量法易受到外界因素干扰,有时难以界定浮泥上下层界面及厚度;耦合测量法精度高,但操作困难。

1.3 浮泥厚度

浮泥冲淤受众多因素影响,准确计算和预测深水浮泥淤积厚度仍有困难,但也有部分学者已从理论推导并结合实测资料拟合了浮泥厚度估算公式。白玉川等[28]基于波浪悬沙和挟沙机理,得到波浪作用下泥沙浓度分布函数,并对河口海岸区域及航道骤淤进行了研究,给出了4种河口骤淤厚度计算方法。针对港池和航道冲淤强度计算问题,国内常采用基于平均概化角度对港池和航道回淤厚度进行计算[29]:

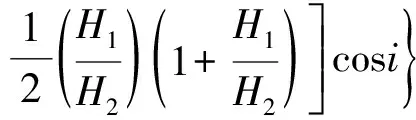
(1)

式中:p为在t时间内的淤积厚度;ωk为泥沙沉速;Sk为浅滩水域含沙量;γ0为淤积物干密度;K1、K2分别为经验系数,取K1=0.35,K2=0.13;H1、H2分别为开挖前后的平均水深;i为水流与航道轴交角。

丁济森等[30]采用刘家驹公式[29]和罗肇森公式[7]对日照港原油码头港池和航道淤积厚度进行了预测,发现这两种方法得到的平均淤积强度及总淤积量很接近。

W．H．MCANALLY 等[31]基于实验数据进行拟合,提出了流体泥浆厚度随时间变化的指数经验计算式:

H=M[1-e-α1 β1 T]2.5

(2)

式中:H为浮泥层厚度;α1、β1分别为系数,基于M(波浪振幅和河床固结程度)确定,分别取α1=0.021 6,β1=0.346;T为时间。

2 浮泥特性

2.1 固结特性

浮泥形成的初始阶段,会发生受阻沉降,之后浮泥会逐渐聚合形成一个边界层,这一过程被称为初次固结;沉降过程中,沉降区上边界层会随时间推移而逐渐下降,直到与河床边界相遇而停止。浮泥固结时间可以持续几小时到几年,固结速率由间隙水或孔隙水从基质中逸出速率控制,即使在脱水结束后,颗粒内部重排也可能造成二次固结[32]。此外,沉积的浮泥在相当长时间内可以抵抗侵蚀,这是因为很可能在流体状态下的浮泥已经达到或接近“胶凝点”,即浮泥在静止足够长时间后,将逐渐形成由颗粒间接触支撑,通过自重排出孔隙水,不断强化固结强度,抵抗再悬浮等影响[33-34]。许宝华[35]进行了室内静水条件下不同浓度浮泥的固结试验,结果表明浮泥在静水条件下固结均需要经历均匀沉降、过度沉降、压缩沉降等阶段,在其他条件相同情况下,含沙量越高,均匀沉降所需的时间越长,过度沉降时间就越短。泥沙絮凝后在骨架尚未形成时,抗剪强度为零,在沉降阶段,重度会迅速增加,当重度达到1.2 g/cm3左右,其增加速度趋缓,进入压实固结阶段。

2.2 流变特性

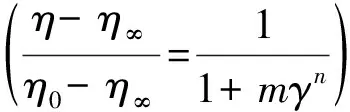
图2 典型流变模型Fig. 2 Typical rheological model

近年来,生物对浮泥流变特性的影响也逐渐引起了学界注意。FANG Hongwei等[41]基于生物膜对流变性影响方面的考虑,测定比较了不同生长阶段的无生物膜和有生物膜泥浆的流变性能,发现水生生物所分泌的生物膜能嵌入和渗透到絮凝沉积物空隙中,使得泥浆初期具有塑性流体的流变特征,且剪切速率与剪切应力成正比,当剪切速率超过规定值时,表面应力却几乎保持不变,当生物膜消失后,流变屈服应力会下降。

2.3 触变性

浮泥除表现出剪切变稀或剪切增稠的现象之外,其流变特性还与时间效应相关,被称为浮泥的触变性[42]。对浮泥触变性认识早期是通过絮凝沉降试验而来。张军[43]在研究黄河泥沙异重流的特性、运动及机制中,分析黏性泥沙絮凝成因时,认为当絮网随着时间调整其结构形态阶段,因流变性质也随时间变化,悬浮体就成为了触变体。E．KNAPPE等[44]研究天然沉积物流变性时发现:半弹性沉积物具有触变性行为,静态屈服应力明显大于动态屈服应力。动态屈服试验结果表明:天然火山附近的海底泥浆在增加应变率与减小应变率部分之间有显著差异,泥浆流变性与微观结构具有时间依赖性,粒子浓度越高,这种滞后现象越明显;静态屈服试验结果表明:泥浆最初为结构化,当克服表观屈服应力后,沉积物会变得非结构化,并开始加速流动。K．DULLAERT等[45]在考虑剪切应力对絮凝颗粒聚集、破裂及布朗运动影响基础上,提出了基于非弹性悬浮介质的触变体系流动特征结构动力学模型,并通过一系列突然变化剪切速率引起的瞬态试验进行评估,结果表明该模型能定量描述因剪切速率突然改变所引起的应力瞬变。FANG Hongwei等[41]在研究生物膜对流变性影响时,观察到生物膜沉积物具有触变性特征,且触变性能反映出污泥在剪切作用下结构强度逐渐破坏的特征性,在剪切速率不变时,触变性表现为剪切应力随剪切时间增加而减小,直到剪切应力不变达到动态平衡状态。

3 浮泥输移

浮泥输移主要受外部风浪、潮流和波浪等动力因素影响,因此目前对浮泥输移的研究主要集中于外部动力条件下的垂直方向上的悬扬和倾斜方向上的重力流。

3.1 悬扬

浮泥形成后与上层水体间存在一个清晰稳定的界面,当水体流速增大到破坏水-泥界面稳定时,浮泥层中大量泥沙会卷入水体中,这被称为浮泥的悬扬。浮泥悬扬主要有两种情况:① 在外部能量及波浪等动力条件输入后,当水流产生剪切应力达到能足够破坏浮泥与上层水体界面时,浮泥中的泥沙颗粒会以悬扬方式向上层水体输移;② 紊流直接冲击静止悬浮层表面,在涡流扰动下颗粒沉积物从表面剥离,从而使高密度泥沙颗粒悬浮,并向上层水体输送。因此,在明确浮泥悬扬的两种情况后,多数学者对浮泥的临界悬扬条件和悬扬率尤为关注,相关研究也主要是围绕量化浮泥临界悬扬条件和悬扬率展开。

3.1.1 临界悬扬条件

第1类研究认为:浮泥为宾汉体,当水流剪切应力大于宾汉应力时,某一流速条件下浮泥泥面失稳进入水体中,应以界面失稳时的水流速度作为临界悬扬流速,建立悬扬起动流速公式。曹祖德[46-47]研究发现:在波浪作用下浮泥容重较小时,浮泥界面将随表面波的震荡面做相应起伏,只有当表面波出现破碎时,界面波才会发生局部破碎而引起浮泥中的泥沙悬浮;当浮泥容重较大,表面波发生作用时,浮泥松动,级配中细小的泥沙颗粒发生悬扬。根据试验资料拟定了悬扬起动流速公式:

(3)

(4)

式中:u0为悬扬起动流速;Δρ为浮泥与水的密度差;ρ为水的密度;h为水深;v为水运动黏性系数;vm为浮泥运动黏性系数;μ0为浮泥和水的相对黏度;τB为宾汉切应力。

第2类研究主要是确定临界悬扬流速与浮泥密度之间的关系。练继建等[48]、范家骅[49]和XU Dong等[50]分别基于水槽试验并结合量纲分析,提出了半经验半理论的黏性泥沙临界悬扬流速公式(表1)。

表1 临界悬扬流速经验公式

表1中:临界悬扬流速Uc与浮泥密度ρm之间存在显著的幂函数关系,且多采用分层流相对密度(ρm-ρ)/ρ关联Uc,浮泥与水的密度差越大,Uc相应增大;黏滞性μ增大,Uc也相应增大[51],而水深h较ρm及μ对Uc影响相对较小。

第3类研究考虑了不同类型泥沙临界悬扬切应力τc与ρm之间的关系,建立了以ρm或淤积物含沙量S为参数的起动判别式[13,52],其一般表达式为:

τc=E1SE2或τc=E3(ρm-ρ)E4

(5)

式中:E1、E2、E3、E4分别为经验系数,其具体参数见表2。

表2 临界悬扬切应力经验系数取值

这类公式考虑因素单一,临界悬扬切应力随浮泥密度增加呈现指数变化趋势,能适用于较大范围密度的黏性泥沙,见图3。但这类公式并没有考虑外部动力条件(如固结沉降、波浪紊流等因素)的影响,可能会导致与实测值有较大误差。

图3 浮泥密度与临界悬扬切应力关系Fig. 3 Relationship between fluid mud density andcritical entrainment shear stress

杨美卿[53]在分析浮泥起动临界状态时,从细泥沙絮凝电化学理论出发,分析了泥沙受力情况,并推导出了Shields参数,含沙量与起动切应力之间的关系式为:

(6)

(7)

式中:θm为Shields参数;d为颗粒粒径;S为淤积物含沙量;Sm为淤泥沉积稳定后的含沙量。

式(6)将有效重力项与颗粒黏着力项考虑在了起动切应力中,在一定程度上能综合反映浮泥的淤积、固结、起动和再悬浮的影响过程,但忽略了浮泥自身的高流动性,因此并不完全适用于浮泥悬扬起动机理。

3.1.2 悬扬率

在考虑涡旋引起的剪切流而导致浮泥悬扬输移时,常构建以浮泥界面的水深变化率(悬扬率)与平均剪切速度或界面摩阻流速之比的无量纲悬扬系数[32,37,54-55],其一般形式为:

(8)

式中:E*为悬扬系数;Ue为悬扬率;U*为混合层平均流速或界面摩阻流速。

Δb1=g(ρ-ρ1)/ρ1

(9)

式中:ρ1为参考密度;h1为上层(低浓度)平均深度。

A．J．MEHTA等[55]从能量平衡角度出发,考虑了浮泥紊动对悬扬率影响,并建立起浮泥紊动层能量平衡方程式:

(10)

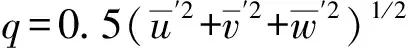
进一步通过量纲分析法并略去盐度扩散项后得到与体积理查森数(Rib)之间的关系:

(11)

(12)

式中:U为混合层平均流速;A、D分别为常数,需要实验确定(A．J．MEHTA等[54]通过拟合曲线测得A=0.005 2,D=0.000 016)。

M．BECKER等[57]研究了河口浑浊带潮下沙丘中浮泥层的悬扬问题,观测到威悉河口潮下沙丘存在主潮引起“卷吸”现象,进一步分析后发现“卷吸”与沙丘后的特定湍流场发展有关,与无强湍流场相比,强湍流场沙丘顶部的湍流应力会加速浮泥层沿泥跃层方向的输移。为此其采用忽略黏性项的悬扬率公式来计算浮泥输移:

(13)

式中:Ue为悬扬率;Rib为体积理查森数;ρ2为泥跃层以上的密度;ρL为泥跃层以下的密度;h为水深。

J．C．WINTERWERP等[58]对英国Crouch河疏浚过程中浮泥的悬扬输移过程进行数值模拟发现:模拟结果与实际观测到的输移扩散结果具有一致性,其悬扬模型为:

(14)

式中:Cs、Cσ分别为悬扬系数,取Cs=0.25,Cσ=0.42;τB=0.2Pa;u*,m为水-泥界面剪切速率;u*,s为扰动项;u为上层水流速;um为流体泥浆层速度。

3.2 重力流

重力流是由泥沙或泥沙-水混合物在重力作用下沿倾斜坡面运动的流体,通常也被称为密度流,其动力机制是在重力作用下因流体微小密度差而保持的运动[32]。在大陆架边缘,存在剧烈的重力驱动流(如浊流)将沉积物输送至深水中的现象,这个沉积物输移过程会对河口演变、海岸形态塑造及航道淤积产生重要影响[59]。学界对浮泥重力流输移机制十分关注,然而目前浮泥重力流的研究手段仍以建立理论模型和现场观测为主。

3.2.1 理论研究

通过建立浮泥平衡坡度模型,探求坡度与浮泥厚度、临界剪切应力之间的关系,揭示浮泥重力流输移机制。唐磊等[60]在分析淤泥质海岸近岸缓坡形成原因时,认为浮泥不是牛顿体,在重力作用下表现为宾汉流体的特征(只有当浮泥层底部剪切应力达到或超过宾汉临界剪切应力时,才会发生流动),从浮泥平衡坡度理论建立模型(图4)为:

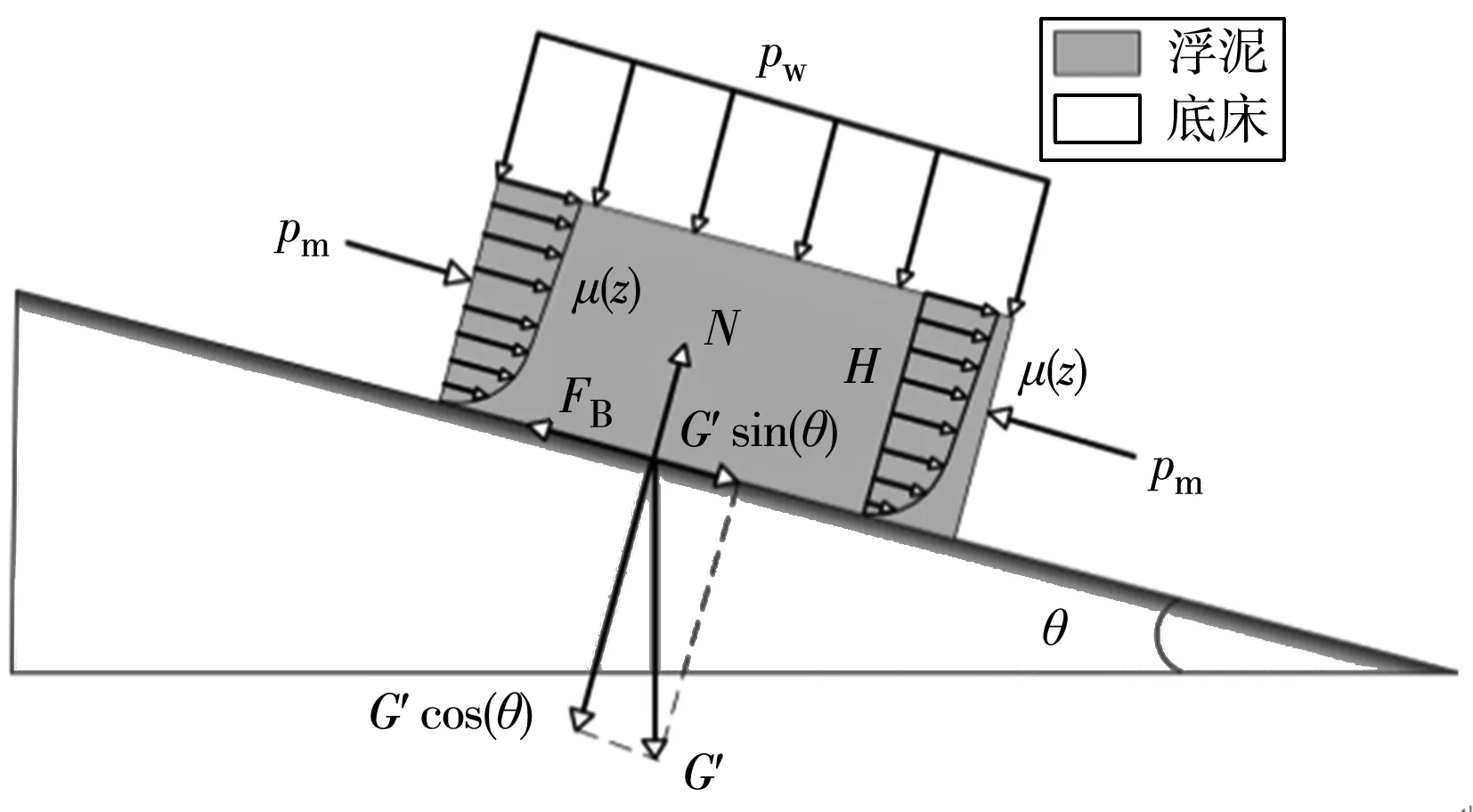
图4 浮泥受力示意Fig. 4 Forces on fluid mud

(15)

式中:G′为有效重力;FB为底部剪切力;Pm为浮泥两端压力(浮泥厚度较小,假定两端压力相等);Pw为水压力;N为上举力。

将式(15)化为切应力形式,可得到浮泥坡度平衡理论模型:

τb=ρmHg′sinθ

(16)

式中:τb为浮泥底部剪切应力;H为浮泥层厚度;ρm为浮泥密度。

进一步可得平衡坡度理论计算式:

(17)

式中:θ为坡度。

洪柔佳等[61]采用宾汉临界剪切应力τB=5.765×10-10e17.706ρm来检验了平衡坡度理论模型的准确性。

3.2.2 现场观测

建立摩擦力与压强梯度力的经验关系式,解释浮泥重力流运动现象。L．D．WRIGHT等[62]对黄河三角洲前缘悬沙扩散现场测量试验表明:底泥主要以重力流的形式向渤海湾浅水区扩散,这些底泥呈羽状沿三角洲前缘下降,用方程来描述羽状重力流的力平衡如式(18):

(18)

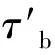
张军[43]研究黄河泥沙异重流形成机制时,忽略科氏力影响,得出了浮泥以异重流形式在斜坡上的摩擦与压强梯度力的平衡关系为:

g″=g(ρd-ρt)/ρt

(19)

式(19)中:h″、β、ρd、g″这4个因素中任何一个改变都会对异重流产生影响,且泥沙浓度是产生异重流的直接因素。在异重流在运动过程中,泥水边界之间存在的湍动混合现象会使泥水与水不断交换,致使ρd、g″不断改变。

P．TRAYKOVSKI等[63]对Eel河沉积物观测时发现:波浪引起重力驱动的流体泥浆在跨陆架输移中占主导地位,且流体泥浆层似乎被表面重力波束缚,在底部区域形成较高浓度后会引发下坡流。建立了跨陆架边界层底部摩擦与科氏加速度及压力梯度间引起的剪应力的平衡式,如式(20):

(20)

式中:f为科里奥利频率;Δv为边界层内与边界层上沿陆架的速度差;g′=gΔρ/ρ,Δρ为浮泥与清水密度差;β为斜坡坡度。

通过实测数据计算后,进一步发现泥浆浓度高于20 kg/m3,科氏力在式(20)中并不是主导因素,略去科氏力并沿垂向积分可得Chzey方程,如式(21):

Hg′sinβ=CdU′2

(21)

式中:H为浮泥层的厚度;Cd为阻力系数(Cd=0.000 8～0.005);U′为泥浆输移速度。

YANG Xiaochen等[64]基于非结构化网格有限体积海岸-海洋模型,从流体泥浆与地层间的摩擦和剪力关系出发,通过建立水-流体-泥浆耦合模型来模拟底层流体泥浆的输移,其剪应力关系如下:

(22)

(23)

式中:ρm、ρ分别为浮泥和水的密度;fs、fm分别为水层、底层与流体泥浆的摩擦系数;u、v分别为泥浆在上部水层x、y方向上的速度;τsx、τsy分别为水-泥浆界面在x、y方向上的剪应力;τbx、τby分别为泥床界面在x、y方向上的剪应力。

近年来,大型河流水库群精细化调度正有序推进,而准确掌握水沙运动规律依旧是精确预测水库淤积形态和库容的基础,是实现水库群减淤优化调度发挥水库综合效益的首要问题[4,65]。胡春宏[66]利用LISST在三峡库区现场观测到库区河段普遍存在泥沙絮团;李文杰等[67]通过实测三峡库区瞬时流速和含沙量,推算出泥沙实际沉速是单颗粒泥沙沉速的10倍,证明库区存在浮泥特征的床面淤积物。水沙数值计算结果也表明不考虑水库淤积物的浮泥特性是导致数值计算结果与实测淤积形态不吻合的关键[68]。假东东等[68-69]认为:三峡水库近坝区泥沙颗粒较细,使得淤积物表现出一定的浮泥特性,引入临界平衡坡度作为浮泥失稳流动判别标准,对近坝区泥沙淤积形态进行模拟,计算结果符合库区实测泥沙淤积形态特征,但未考虑浮泥流变特性;随后考虑小浪底水库浮泥宾汉体流变特性,将式(23)、式(24)应用于小浪底水库淤积形态数值模拟中,对小浪底库区床面淤积形态进行了分析,并与实际细颗粒泥沙输移冲淤分布进行对比,表明了该剪应力模型也适用于描述水库淤泥输移,但研究中并未深入考虑黏性泥沙复杂理化性质和外部水动力荷载对浮泥流变特性的影响。

李昆鹏等[19]对小浪底水库浮泥在后期异重流运行响应方面进行了研究,通过原型观测数据,发现水库中存在浮泥,且水库中的不动浮泥层厚度在异重流发生后会显著减少,间接说明了水库浮泥输移或能以异重流的形式进行。李涛等[70]在分析黄河水沙特性基础上,对洪水异重流与浮泥作用水槽进行了试验研究,表明水库浮泥不仅会影响当次洪水泥沙输运,也会对后续洪水异重流输运有明显影响;通过分析浮泥宾汉塑性体流变特性和异重流有效切应力,提出了浮泥运动判别数,但该研究未考虑外部水动力条件和沉积环境对浮泥流变特性的影响。张俊华[4]对小浪底水库输沙规律进行了研究,指出在洪水能量不足,异重流继续前进或异重流运行至坝前闸门未及时开启时,就地停滞会产生浮泥层,其根据后续异重流和前期浮泥层之间是否有混掺而定义了侵入型和界面型流动,并给出了浮泥特征厚度,如式(24):

(24)

式中:I为水库浮泥层流动判别数;hm为水库浮泥层厚度;J为浑液面比降;Si为异重流含沙量;C为经验系数,小浪底水库C=1.84×10-21。

当I>1,浮泥层方可流动;I≤1,浮泥层停滞;当I=1时,可得到水库浮泥层临界特征厚度hmc。

(25)

综上,浮泥成为影响水库淤积的主要因素之一,浮泥层对水库淤积物分布形态和后续异重流输沙具有明显影响。目前,大型水库浮泥问题虽已引起学者们重视,且研究成果对大型水库浮泥运动特性给予了一定解释,但尚缺乏针对浮泥层生成机制和运动规律的系统探究。