地震作用下岩石裂纹扩展角度研究

高丙丽　曹孝杰

摘 要：为研究地震作用下岩石动态开裂的复杂问题，基于最大周向应力准则，考虑非奇异应力三分量及地震作用，推导出了适用于地震作用下的裂纹扩展角度判据；采用霍普金森拉杆试验结果对修正裂纹扩展角度判据可靠性进行验证，针对验证过程中样本数较少的情况，基于贝叶斯理论，开发了岩石领域小样本问题后验分布估计程序，并采用该程序进一步验证修正裂纹扩展角度判据的可靠性。结果表明：在霍普金森拉杆试验中，MCTS试样可以通过施加位移约束，实现可控模式复合比的复合型加载；最大周向应力判据、修正最大周向应力判据对霍普金森拉杆试验中的MCTS试样裂纹扩展角度预测值平均误差分别为1.6°、1.37°；以试验值、最大周向应力判据预测值、修正最大周向应力判据预测值为基础数据运行Gibbs算法分别进行十万次迭代，求得这三种情况下的裂纹扩展角度均值分别为50.64°、48.96°、49.45°，修正最大周向应力判据与最大周向应力判据相比，其预测误差由3.32%降低到了2.35%，表明其在地震作用下具有良好的适用性。研究对地震作用下的边坡危岩减抗震设计及其风险控制具有重要意义。

关键词：地震作用；非奇异应力；裂纹扩展；霍普金森拉杆；贝叶斯理论

中图分类号：TU 452文献标志码：A 文章编号：1672-9315（2023）05-0980-08

DOI：10.13800/j.cnki.xakjdxxb.2023.0515

Research on rock crack propagation angle  under earthquake action

GAO Bingli，CAO Xiaojie

Abstract：In order to study the complex problem of dynamic cracking of rocks under earthquake action，a crack propagation angle criterion is derived based on the maximum circumferential stress criterion，with the non-singular stress triplet component and earthquake action in view.The posterior distribution estimation procedure for small sample problems in the domain is designed based on Bayesian theory，and the procedure is used to further verify the reliability of the modified crack propagation angle criterion.The results show that the MCTS specimens in split Hopkinson tension bar test can be loaded in a composite manner with controlled mode composite ratio by applying displacement constraints.The average errors of the predicted values of the maximum circumferential stress criterion and the modified maximum circumferential stress criterion for the crack propagation angle of MCTS specimens in split Hopkinson tension bar test are 1.6° and 1.37°，respectively.The Gibbs algorithm was run for 100 000 iterations to obtain the mean values of 50.64°，48.96° and 49.45° for the crack propagation angles in these three cases，respectively，and the prediction error of the modified maximum circumferential stress criterion was reduced from 3.32% to 2.35% compared with that of the maximum circumferential stress criterion，which shows that it has good applicability under earthquake effects.The study is of great significance for the seismic design of slope hazardous rock and its risk control under seismic action.

Key words：earthquake action；T－stress；crack propagation；Hopkinson tension bar；Bayesian theory

0 引 言

無论是危岩体，还是矿山、岩质边坡、隧道等岩体工程中的岩石，他们在外界环境中的破裂与失稳，都是其内部微裂纹起裂、扩展、贯通的宏观表现[1-3]。因此，对岩石中裂纹扩展特性进行研究，一直是当今岩石破坏与失稳研究的热点问题。岩石裂纹扩展准则及其相关判据的研究已经受到许多关注[4-5]，但是动荷载作用下，尤其是地震等波动作用下的裂纹扩展特性研究仍存在很多不足。建立适用于地震作用下的裂纹动态扩展判据，是准确分析地震作用下岩体工程稳定性的前提。

广义最大周向应力准则（GMTS）被广泛应用于岩石裂纹扩展研究中，但是其仅考虑了节理尖端应力场分布中奇异应力项的影响，而忽略了非奇异应力项（T应力）的影响[6-8]。随着研究逐渐深入，学者发现T应力对裂纹扩展方向，扩展角度及裂纹扩展稳定性等方面都存在一定影响。COLOMBO等认为正T应力会使得裂纹尖端应力集中更为明显，而负T应力则会屏产生屏蔽效应，这使得断裂韧度会随着T应力的改变而改变[9]。MATVIENKO等对石灰岩混合型裂纹的断裂扩展角进行预测，发现考虑T应力后断裂扩展角与试验结果更为接近[10]。SIMTH等研究了复合型外荷载作用下，当裂纹为直线形时，T应力对其开裂角度和脆性断裂的影响[11]。但是上述研究结果均只考虑了T应力沿裂纹面方向的应力分量Tx，随着研究的深入，学者对平行和垂直于裂纹表面的T应力分量同时展开了研究。LI等研究了压缩条件下的闭合裂纹，发现沿裂纹方向的分量Tx和垂直于裂纹方向的分量Ty在裂纹尖端同时存在，并发现Tx将减小翼裂纹起裂角，并增加Ⅱ型裂纹的断裂韧度，而Ty则增加翼裂纹起裂角，并增加Ⅱ型裂纹的断裂韧度[12]。唐世斌等发现非奇异应力项Tx，Ty会影响压剪岩石裂纹起裂及扩展[13]。王俊杰等引入相对钝化系数和相对临界尺寸，建立了考虑裂缝几何特性和Tx，Ty的压剪张拉断裂准则。学者们对T应力的研究使得最大周向应力准则的使用范围和精确性得到了提高[14]。

现有研究大部分只考虑了平行（Tx）和垂直（Ty）于裂纹表面的T应力分量，而忽略了T应力分量Txy。而且研究集中在静力或拟静力作用下的岩石，对动荷载作用下，尤其是地震等波动作用下的裂纹扩展特性研究仍存在很多不足。在地震等波动作用下，岩石裂纹面可能会发生闭合，此时裂纹面之间将在外力作用下相互影响并产生摩擦作用。摩擦力的存在势必阻止裂纹面的相互滑动，因此Txy不应被忽略。更关键的是学者对动荷载作用下的裂纹扩展准则研究聚焦于对动态应力强度因子的求解上。随着应变片以及光学测量技术的发展，学者们对相对位移法[15]、J积分法[16]、应变片法[17]等动态应力强度因子计算方法展开了研究，并且取得了一些成果[18-20]。但是却忽略了动荷载本身也会对裂纹尖端应力场产生影响，这使得采用现有裂纹扩展准则无法很好的预测地震等动荷载作用下的岩石裂纹扩展。

通过考虑T应力三分量及地震作用，对GMTS准则进行了修正，使其能准确预测地震作用下的岩石裂纹扩展角度。并采用霍普金森拉杆试验数据对其可靠性进行验证。针对试验数据较少的情况，基于Bayes理论，采用Open BUGS语音编写了岩石领域小样本问题后验分布估计程序，从而对试验和理论推导数据进行再处理，形成均值化指标，进一步验证了修正GMTS准则的有效性。

1 修正GMTS准则的推导

裂隙岩石常处于多向受压的力学环境中，其裂纹扩展力学模型可以简化如图1所示。

分析地震作用对岩体应力状态影响的常用方法是将地震力转化为应力形式。其步骤为先将地震波的加速度利用公式变换成速度时程，然后根据岩石动力学中的波动理论公式，即可得到地震产生的动应力公式。

考虑地震作用的裂隙岩石裂纹扩展力學模型如图2所示。其在压缩条件下的裂纹扩展力学模型的基础上，考虑了地震产生的竖向应力σn和地震产生的水平应力σs。

为了研究地震作用对岩石裂纹扩展的影响，取裂纹尖端微单元（图3）进行分析。其中r为极径；θ为极角；σθ，σr和τrθ分别为周向应力、径向应力和剪应力。

为了更加直观的表达裂纹尖端的应力场，WILLIAMS将裂尖应力场展开为满足裂纹面应力边界条件的一系列特征函数的求和[21]，其中奇异应力项为KⅠ或KⅡ，在裂纹尖端起主导作用。非奇异应力项即T应力，对裂纹尖端的影响随着临界尺寸的增大而增大。现有研究大部分只考虑了平行（Tx）和垂直（Ty）于裂纹表面的T应力分量，而忽略了T应力分量Txy。在地震等波动作用下，岩石裂纹面可能会发生闭合，此时裂纹面之间将在外力作用下相互影响并产生摩擦作用。摩擦力的存在势必阻止裂纹面的相互滑动，因此不应被忽略。

同时要准确计算地震荷载下的T应力，就必须考虑地震对T应力的影响。上文已得到地震所产生的竖向应力σn和水平应力σs，将其代入T应力中，即可得到考虑了地震作用的T应力三分量。将考虑了地震作用的T应力三分量引入裂纹尖端应力场，并取最大周向应力准则的裂纹扩展临界状态，即可得到考虑T应力三分量的最大周向应力裂纹扩展角度判据。

为了更加直观的体现修正GMTS判据与GMTS判据的区别，以中心直裂纹巴西圆盘模型（图4）为例，取纵向载荷P=10 MPa，弹性模量E=20 GPa，泊松比μ=0.2，并假设无量纲特征距离d=0.5，σn，σs均取零，并使用MTS、GMTS、修正GMTS准则计算裂纹扩展角度预测值（图5）。

在裂纹倾角大于45°时，MTS裂纹扩展角度预测值（黑色曲线）大于GMTS裂纹扩展角度预测值（红色曲线）和修正GMTS裂纹扩展角度预测值（蓝色曲线），说明T应力对扩展角存在抑制作用，减小了扩展角。在裂纹倾角小于45°时，则恰好相反，T应力会使扩展角增大。

而GMTS、修正GMTS裂纹扩展角度预测值曲线存在多处交叉点，表明地震作用对裂纹扩展角度没有明显的促进或抑制作用，相对于原始判据是否更加准确，可通过试验测得数据进行分析。

2 试验结果对比

聚甲基丙烯酸甲酯材料（PMMA）在低温下会呈现良好的脆性，可以近似模拟岩石的脆性破裂行为，而且其均质性可减小材料性质对试验结果的影响。谌赫采用PMMA材料制备MCTS试样作为样品，并采用霍普金森拉杆试验系统以30°、45°、60°分别对MCTS试样进行加载（图6）[22]。

加载后试样破碎成若干块，并在孔边发生破坏（图7）。特别是加载角度30°的试样在预制裂纹和切口处出现多个不同方向的裂纹，并观察到裂纹扩展方向发生拐折，这是由于裂纹发生扩展之后加载并没有停止而造成的持续破坏，因此应以预制裂纹尖端处的初始扩展方向为准测量起裂角度。

基于试验测得数据，使用文献[23]提出的方法，得到加载角度为30°、45°、60°时MCTS试样的动态应力强度因子曲线（图8）。

当加载角度为30°和45°时，应力强度因子存在震荡现象，其原因是MCTS试样与夹具存在装配间隙，从而导致加载过程中试样孔边发生局部滑动，其应力波的传播路径也会发生偏折。从图7也可以看出，破坏后的试样在孔边发生一定程度的塑性变形，在加载角度为30°时尤为明显。

不同加载角度的MCTS试样裂纹均在0.785 ms附近开始扩展，这表明加载角度对MCTS试样扩展时间影响不大。不同加载角度下，KⅠ和KⅡ虽然大小不一样，但是其变化的趋势基本相同。尤其是加载角度为30°时，在0.735～0.785 ms，KⅠ和KⅡ的变化趋势高度相似，这验证了文献[24]采用MCTS试样来控制复合比加载的可行性。同时，和 变化趋势相同也证明试验所测得数据较为准确，则采用该试验数据对修正GMTS准则进行验证的可信度较高。

采用GMTS判据、修正GMTS判据分别计算加载角度为30°、45°、60°情况下的扩展角度预测值，其中Rc=2 mm。图9为0.700～0.785 ms的MCTS试样扩展角度预测值。

在3种加载角度下，修正GMTS判据与GMTS判据在裂纹扩展时刻的裂纹扩展角度预测值之间的差距并不大。但是修正GMTS判据预测的最大值大于GMTS判据，而最小值小于GMTS判据，这使得两种判据的幅值之差已较为明显。可以预测，在振幅大，持续时间长的强震作用下，两种判据的预测值之间的差距会进一步扩大。

将修正GMTS判据则与GMTS判据在裂纹扩展时刻的裂纹扩展角度预测值与试验测得的裂纹扩展角度汇总见表1。

采用修正GMTS判据对裂纹扩展角度行预测，其平均误差相对于GMTS判据由-1.60°变为了-1.37°，扩展角度方差由3.16减少到了2.40，预测准确度明显提升。但是文献[23]由于只有3个MCTS试样，只得到了3组裂纹扩展角度数据。虽然已经使用PMMA材料来排除材料性质对结果的影响，但由于试验操作、试验设备等不可控因素，试验结果与真实值之间仍会存在一定的误差。但由于试验样本数过少，采用常规数值拟合的方式会使得结果偏差较大，而数值模拟方法更多的是用来对规律进行分析。Bayes方法在处理这种小样本问题中有着广泛的应用。

3 修正GMTS准则可靠性

Bayes方法[25-26]的核心是通过引入新的信息来对当前结果进行不断的修正，伴随引入信息量的增加，评估结果与真实结果也会越发接近。但想要获得准确的参数值，需要大量的数据作为支撑，其成本花费巨大。计算机的发展使得样本的迭代变得简便，而更多次数的迭代让结果变得更加准确。

Bayes理论在裂纹领域小样本问题中有着广泛的应用[27]，其主要步骤如下。

先验分布的确定是后续计算的前提，合适的先验分布的选取能减少计算工作量并提升结果准确度。Weibull分布在可靠性评价中的应用较为广泛，对于巖石可靠性评价也具有良好的适用性，选用Weibull分布作为先验分布。

联合分布的推导是将Weibull分布与Bayes理论联系的关键。将Weibull分布的概率密度函数代入Bayes公式，计算得到联合分布的似然函数。

后验分布的准确求解是方法的核心，求解的准确性直接决定可靠性研究的准确性。由于Weibull分布的复杂性，其参数后验分布无法通过解析式求解，需借助计算机编程对其进行计算。通过Open BUGS软件运行Gibbs算法求解Bayes后验概率，采用BUGS语言开发了岩石领域小样本后验分布估计程序。

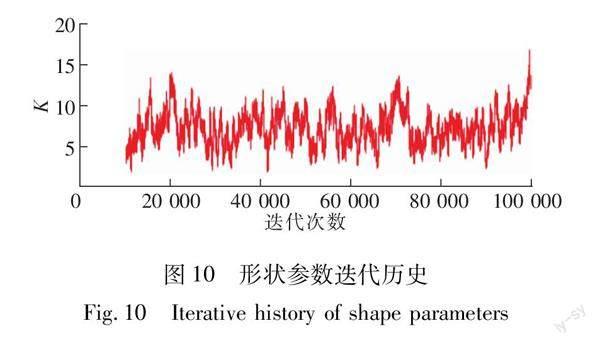
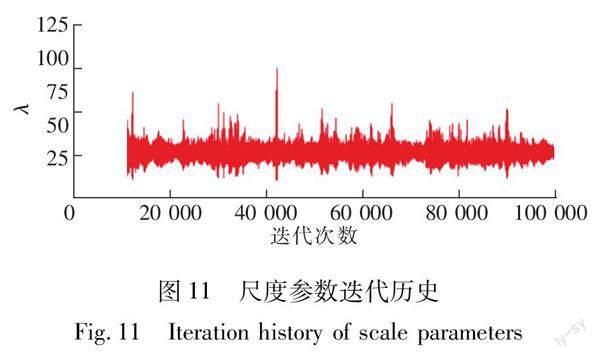
设置2条chains，进行一万次迭代，当2条chains图像均在固定区域内，且幅值相近，则表示此时MCMC算法已收敛，可进行参数分析。设置迭代次数为十万次，退火次数为一万次，形状参数K和尺度参数λ迭代过程如图10、图11所示。

通过对比形状参数与尺寸参数迭代历史图可以发现，形状参数的迭代数据相比于尺寸参数更为离散。这是因为在Weibull分布中，形状参数是以指数函数的形式对整体分布产生影响，而尺寸参数是以一次函数的形式对整体分布产生影响，所以尺寸参数的曲线更为连贯，表现为图11相对于图10，其曲线更为密集。两条曲线的迭代值始终在固定范围内，整体结果为收敛，证明先验分布的选取是合理的。

取中位数作为参数估计的结果，则K=6.941，λ=52.89。由Weibull分布的均值计算公式计算可得E=49.45。同理，可计算得到GMTS准则的裂纹扩展角度均值为48.96°，试验扩展角度均值为50.64°。

E不代表具体的裂纹扩展角度，其意义为在材料和其他加载条件确定的情况下，当加载角度处于30°～60°时，该材料所有可能扩展角度的均值。试验与修正GMTS准则、GMTS准则之间的裂纹扩展角度均值之差分别为1.19°和1.68°。可以看出，采用修正GMTS准则对裂纹扩展角度进行预测，其误差相对于GMTS准则由3.32%降低到了2.35%。

4 结 论

1）基于最大周向应力准则，同时考虑T应力三分量及地震作用，推导出适用于地震荷载作用下的岩石裂纹扩展角度判据。

2）不同加载角度情况下，MCTS试样的KⅠ和KⅡ变化趋势基本相同，验证了MCTS试样可以通过施加位移约束，实现可控模式复合比的复合型加载。KⅠ和KⅡ变化趋势相同也证明试验所测得数据较为准确，则采用该试验数据对修正GMTS准则进行验证的可信度较高。

3）采用霍普金森拉杆试验结果和贝叶斯理论对修正最大周向应力裂纹扩展判据的可靠性进行验证，其结果表明修正判据相对于原始判据在地震等波动作用下的预测结果更为准确。

参考文献（References）：

[1] 杨亮，杨永涛，郑宏.相场数值流形法模拟岩石裂纹扩展[J].岩土力学，2021，42（12）：3419-3427.

YANG Liang，YANG Yongtao，ZHENG Hong.The phase field numerical manifold method for crack propagation in rock[J].Rock and Soil Mechanics，2021，42（12）：3419-3427.

[2]李晓照，戚承志，邵珠山.岩石裂纹扩展诱发的强度弱化模型研究[J].地下空间与工程学报，2020，16（1）：26-34.

LI Xiaozhao，QI Chengzhi，SHAO Zhushan.Study on strength weakening model induced by rock crack propagation[J].Journal of Underground Space and Engineering，2020，16（1）：26-34.

[3]李樹刚，成小雨，刘超.类岩石材料压缩破坏力学特性及裂纹演化特征[J].西安科技大学学报，2017，37（6）：771-778.

LI Shugang，CHENG Xiaoyu，LIU Chao.Mechanics and crack evolution characteristics of rock－like material under compression failure[J].Journal of Xian University of Science and Technology，2017，37（6）：771-778.

[4]侯铁军，满宇，唐巍.基于最大周向应变的岩石复合型断裂准则解析与验证[J].煤炭科学技术，2021，49（3）：78-82.

HOU Tiejun，MAN Yu，TANG Wei.Analysis and verification of rock mixed mode fracture criterion based on maximum circumferential strain[J].Coal Science and Technology，2021，49（3）：78-82.

[5]乔宝明.裂纹应力强度因子的有限元计算[J].西安科技大学学报，2010，30（5）：629-632.

QIAO Baoming.Finite element calculation of crack stress intensity factor[J].Journal of Xian University of Science and Technology，2010，30（5）：629-632.

[6]WILLIAMS J G，EWING P D.Fracture under complex stress：The angled crack problem[J].International Journal of Fracture，1974，8：416-441.

[7]SMITH D J，AYATOLLAHI M R，PAVIER M J.The role of stress in brittle fracture for linear elastic materials under mixed－mode loading[J].Fatigue and Fracture of Engineering Materials and Structures，2001，24：311-321.

[8]ALIHA M R M，AYATOLLAHI M R.Analysis of fracture initiation angle in some cracked ceramics using the generalized maximum tangential stress criterion[J].International Journal of Solids and Structures，2012，49：1877-1883.

[9]COLOMBO C，DU Y，JAMES M N.On crack tip shielding due to plasticity－induced closure during an overload[J].Fatigue Fracture Engineering Material Structure，2010，33（12）：766-777.

[10]MATVIENKO Y G.Maximum average tangential stress criterion for prediction of the crack path[J].Internatio－nal Journal of Fracture，2012，176（1）：113-118.

[11]SIMTH D J，AYATOLLAHI M R，PAVIER M J.The role of T－stress in brittle fracture for linear elastic materials in mixed－mode loading[J].Fatigue Fracture Engineering Material Structure，2001，24（2）：137-150.

[12]LI X F，LIU G L，LEE K Y.Effects of T－stresses on fracture initiation for a closed crack in compression with frictional crack faces[J].International Journal of Fracture，2009，160（1）：19-30.

[13]唐世斌，黄润秋，唐春安.T应力对岩石裂纹扩展路径及起裂强度的影响研究[J].岩土力学，2016，37（6）：1521-1529，1549.

TANG Shibin，HUANG Runqiu，TANG Chunan.Effect of T－stress on crack growth path in rock and fracture strength[J].Rock and Soil Mechanics，2016，37（6）：1521-1529，1549.

[14]王俊杰，黄诗渊，郭万里.考虑裂缝几何特性和T应力的类岩石材料压剪张拉断裂准则[J].岩土工程学报，2020，42（9）：1622-1631.

WANG Junjie，HUANG Shiyuan，GUO Wanli.Compression－shear－tension fracture criterion of rock－like materials considering crack geometry and T－stress[J].Chinese Journal of Geotechnical Engineering，2020，42（9）：1622-1631.

[15]LIU R F，ZHU Z M，LI M，et al.Study on the initiation and propagation of mode I cracks under blast loading[J].Journal of Rock Mechanics and Engineering，2018，37（2）：392-402.

[16]WANG H J，LI H Z，REN R，et al.Study on crack propagation law and failure characteristics in three－point bending brittle solid based on 3D－ILC[J].Journal of Rock Mechanics and Engineering，2019，38（12）：2463-2477.

[17]李清，于强，徐文龙，等.应变片法确定Ⅰ型裂纹动态应力强度因子试验研究[J].岩土力学，2018，39（4）：1211-1218.

LI Qing，YU Qiang，XU Wenlong，et al.Experimental study on determination of dynamic stress intensity factor of mode Ⅰ crack by strain gauge method[J].Geotechnical Mechanics，2018，39（4）：1211-1218.

[18]WANG Y B，LUO L，CHEN J L，et al.Dynamic mecha－nical behavior and macroscopic and microscopic characteristics of granites subject to heating treatment[J].Arabian Journal of Geosciences，2023，16（2）：112-130.

[19]LIU K W，GUO T F，YANG J C，et al.Static and dyna－mic fracture behavior of rock－concrete bi－material disc with different interface crack inclinations[J/OL].Theoretical and Applied Fracture Mechanics，123，103659.https：//doi.org./10.1016/j.tafmec.2022.103659.

[20]劉邦，朱哲明，刘瑞峰，等.爆炸作用下隧道拱肩Ⅰ/Ⅱ复合型裂纹起裂及扩展规律研究[J].岩石力学与工程学报，2021，40（10）：2048-2061.

LIU Bang，ZHU Zheming，LIU Ruifeng，et al.Study on crack initiation and expansion of tunnel arch shoulder Ⅰ/Ⅱ composite cracks under the effect of explosion[J].Journal of Rock Mechanics and Engineering，2021，40（10）：2048-2061.

[21]WILLIAMS M L.On the stress distribution at the base of a stationary crack[J].Journal of Applied Mechanics，1956，24：109-114.

[22]LIU B，ZHU Z M，LIU R F，et al.Study on crack initiation and expansion of tunnel arch shoulder Ⅰ/Ⅱ composite cracks under the effect of explosion[J].Journal of Rock Mechanics and Engineering，2021，40（10）：2048-2061.

[23]谌赫.复合型动态加载下裂纹起裂与扩展行为研究[D].哈尔滨：哈尔滨工程大学，2020.

CHEN He.Study on crack initiation and extension behavior under composite dynamic loading[D].Harbin：Harbin Engineering University，2020.

[24]王自强，陈少华.高等断裂力学[M].北京：科学出版社，2009.

[25]秦正积，严晓玲，沈毅.OpenBUGS处理结构方程模型贝叶斯分析在SAS宏程序中的实现[J].中国卫生统计，2020，37（3）：475-480.

QIN Zhengji，YAN Xiaoling，SHEN Yi.The implementation of Bayesian analysis of structural equation model in SAS macro program[J].China Health Statistics，2020，37（3）：475-480.

[26]王有元.基于Bayes方法及其改进的无失效数据和小子样产品可靠性评估[D].成都：电子科技大学，2022.

WANG Youyuan.Reliability assessment of zero－failure data and small－sample products based on Bayes method[D].Chengdu：University of Electronic Science and Technology，2022.

[27]李美艳.基于Bayes理论的球罐裂纹概率分布模型研究[D].杭州：浙江工业大学，2019.

LI Meiyan.Research on probability distribution model of spherical tank crack based on Bayes theory[D].Hangzhou：Zhejiang University of Technology，2019.

（责任编辑：李克永）

收稿日期：2023-05-25

基金项目：国家重点研发计划项目（2019YFC1509703）

通信作者：高丙丽，女，河南许昌人，博士，副教授，E－mail：gbl8001@126.com