基于价值分解深度强化学习的分布式光伏主动电压控制方法

刘 硕，郭创新，冯 斌，张 勇，王艺博

（1.浙江大学 电气工程学院，浙江 杭州 310027；2.国家电网有限公司华北分部，北京 100053）

0 引言

近年来，能源短缺、环境污染等问题日益严峻，随着“双碳”目标的提出、“屋顶光伏”政策的出台，光伏等新能源得到了大力发展［1］。截至2022 年底，我国累计光伏容量达到3.92×108kW，其中分布式光伏占比为40.21 %。大量分布式光伏的接入，使原有的潮流走向发生改变，导致末端电压严重越限，网络损耗急剧增加［2］。光伏出力的不确定性、随机性也造成节点电压频繁波动，电能质量显著降低，无法保证用户负荷的可靠供电。配电网作为分布式光伏的主要接入对象，面临经济、安全、稳定运行的巨大挑战［3］。

与此同时，受益于数字化技术的发展，配电网逐渐由被动受控模式转变为具有主动调控能力的智能系统。光伏逆变器连续可调的无功输出能力为主动配电网提供了更加灵活的调度手段［4］。光伏逆变器响应速度快，控制精度高，具有较好的灵活性和经济性，能够满足在线应用要求［5］。利用分布式光伏逆变器进行无功功率补偿，优化潮流分布，抑制电压波动，降低线路损耗，实现主动电压控制，已成为主动配电网调度运行的关键技术［6］。

目前，主动电压控制主要面临精确性不足、实时性较差［7］的问题。传统的数学优化方法需依赖精确的物理模型［8］，而低压配电网的感知度往往较低，无法获取完整的网络参数。此外，优化问题的复杂度会随着控制变量的增多而急剧增长，且考虑到源荷不确定性、交流潮流约束［9］，这类高维非线性优化问题的求解效率较低，计算耗时较长，难以实现在线调控。

随着人工智能技术的发展，深度强化学习（deep reinforcement learning，DRL）方法在电网优化运行领域得到了广泛的关注［10］。DRL作为一种无模型的数学驱动方法［11］，摆脱了对精确参数的依赖，能够从历史经验中学习到泛化的控制策略，在执行过程中只需要进行神经网络的前馈运算，可以满足精确性、实时性的要求。文献［12］采用行动者-评论家算法来拟合离散无功调节设备的投切指令，实现了低感知度配电网的无功优化，但所提方法无法对连续设备进行调节。文献［13］基于深度确定性策略梯度（deep deterministic policy gradient，DDPG）算法制定无功出力计划，实现了连续电压控制。上述研究将所有无功设备视为统一的智能体，但实际上由于通信负担、控制时延等问题，配电网难以进行集中控制［14］，因此需要将每台设备视为单独的智能体，采用多智能体DRL 方法［15］进行分布式控制。文献［16］采用多智能体深度确定性策略梯度（multi-agent DDPG，MADDPG）算法协调控制多台无功设备，在实现稳压减损的同时降低了通信成本，保证了决策的实时性。文献［17］在MADDPG 算法的基础上进行双延迟改进，进一步提升了算法的性能。

然而，上述MADDPG 算法存在信用分配、过度泛化等问题，导致其在面对复杂多变的配电网环境时存在策略学习能力有限、主动电压控制的性能表现欠佳问题。一方面，MADDPG 算法使用全局价值网络对所有智能体的整体动作进行打分，无法分辨个体动作的贡献程度，这就容易导致“懒惰智能体”的出现，即在其他智能体已经学习到较好策略的情况下，某些智能体不再进行探索更新。另一方面，MADDPG 算法在进行策略学习时，选取其他智能体的历史动作进行评分指导，并对每个智能体分别进行参数更新，这会导致最终的策略易陷入次优解，各设备之间无法做到有效协调［18］。

针对上述问题，本文提出一种基于价值分解的MADDPG（value decomposition based MADDPG，VDMADDPG）算法。首先，介绍分布式光伏逆变器的无功调节原理，建立主动电压控制问题的分布式部分可观测马尔可夫决策过程（decentralized partially observable Markov decision process，Dec-POMDP）模型；然后，在MADDPG 算法的基础上，引入分解式价值网络和集中式策略梯度2 项改进措施，构成VD-MADDPG 算法，并介绍其架构和流程；最后，以改进的IEEE 33 节点配电网系统为算例进行仿真分析。结果表明，所提VD-MADDPG 算法能有效改善潮流分布，缓解电压越限，降低网络损耗，且收敛速度更快，对复杂场景的鲁棒性更强。

1 含高比例光伏配电网的主动电压控制问题

1.1 分布式光伏逆变器的无功调节

本文利用配电网中分布式光伏逆变器输出的无功功率来平抑电压波动，缓解电压越限问题，并尽可能地降低网络损耗，从而实现主动电压控制。假设总控制周期为T，配电网中共有M个节点和N台光伏，用t、m、n分别表示时刻、节点、光伏索引号。主动电压控制的目标函数为：

式中：QPV，n，t为t时刻第n台光伏逆变器的无功出力；Um，t为t时刻节点m的电压幅值；U0为电压基准值；Ploss，t为t时刻系统网络损耗；α为协调因子，用来平衡电压偏差和网络损耗。

为了积极响应国家的“双碳”目标和“整县光伏”政策，保证新能源充分消纳，避免出现弃光现象，本文假设光伏在白天工作在最大功率点跟踪模式，在夜晚工作在静止同步补偿器模式，因此不削减光伏的有功出力，仅调节逆变器的无功出力。光伏逆变器的无功出力QPV，n，t所能调节的范围与其额定视在容量Sn，max和实时有功出力PPV，n，t相关，关系式为：

光伏的额定视在容量一般约为其最大有功出力的1.1倍［19］，即使在夏季正午时段光伏有功功率满发的情况下，逆变器的最大无功出力仍能达到光伏有功出力的45.8 %［17］。而在其他时段，光伏逆变器的无功调节潜力更加可观。因此，利用分布式光伏逆变器进行无功调节，可以较好地满足主动电压控制的调度需求。

1.2 主动电压控制问题的马尔可夫决策过程建模

由于难以精确获取配电网的模型参数，且新能源出力的快速波动对决策的实时性提出了较高的要求，传统的数学优化方法已无法适应当前控制场景。而DRL 的应用能够有效地解决上述不足，实现无模型数据驱动和实时决策控制。使用DRL 方法需要将问题建模为马尔可夫决策过程，又由于受到通信时延、隐私保护的限制，分布式光伏只能观测到局部区域的信息，因此本文将主动电压控制问题建模为Dec-POMDP。

Dec-POMDP 由元组(s，o，a，r，K，γ)组成，其中：s、o、a、r分别为智能体的状态、观测、动作、奖励；K为状态转移函数，表示环境根据当前状态、动作转移至下一状态的概率；γ为折扣率，表示对未来回报的关注度。DRL 的目标是寻找最优的联合控制策略，使累计折扣回报最大。本文采用下标n表示单个智能体的个体变量，用来区分所有智能体的联合变量。

针对主动电压控制问题，配电网中每台分布式光伏均可视为1 个单独的智能体，Dec-POMDP 相关变量的具体含义如下。

1）状态st={fm，t|m=1，2，…，M}。st为t时刻所有 节 点 特 征 量 的 集 合，fm，t=[PL，m，t，QL，m，t，PPV，m，t，QPV，m，t-1，Um，t-1，δm，t-1]为t时刻节点m处的特征量，其中：PL，m，t、QL，m，t分别为t时刻节点m处负荷的有功、无功功率；PPV，m，t为t时刻节点m处光伏逆变器的有功出力；QPV，m，t-1为t-1 时刻节点m处光伏逆变器的无功出力；Um，t-1、δm，t-1分别为t-1时刻节点m的电压幅值、相角。若节点m处没有负荷或光伏，则相应的功率为0。

2）观测ot={on，t|n=1，2，…，N}。联合观测ot由各智能体的局部观测on，t组成。单个智能体只能观测到区域内的节点特征量，即on，t={fm，t|m∈Mn}，Mn为智能体n所在区域的节点集合。

3）动作at={an，t|n=1，2，…，N}。联合动作at由各智能体的个体动作an，t组成，其中an，t=QPV，n，t，即智能体n的动作为当前时刻光伏逆变器的无功出力。

4）奖励。在本文问题中各智能体为完全合作关系，通过相互协调使得系统电压偏差和网络损耗最小，因此智能体之间共享奖励。将式（1）中单个时刻的目标函数取反，构成全局奖励rt，如式（3）所示。

5）状态转移。在当前的运行状态下，分布式光伏根据自身的策略控制逆变器输出无功补偿功率，电网潮流重新分布，节点电压和网络损耗发生改变，光伏有功出力和负荷功率随机波动，由此转移到下一时刻的状态。

2 面向电压控制的价值分解DRL

分布式光伏的输出连续可调，针对此类多智能体连续控制问题，经典的DRL 为MADDPG 算法。MADDPG 算法训练简单，实现方便，但存在信用分配、过度泛化等问题，在面对复杂多变的电网环境时控制效果欠佳。因此，下面在MADDPG 算法的基础上，引入分解式价值网络、集中式策略梯度2项改进措施，提出VD-MADDPG算法，并介绍算法架构及流程。

2.1 MADDPG算法

MADDPG 算法采用行动者-评论家神经网络结构，如附录A 图A1 所示，其中包含N个策略网络μn和1 个全局价值网络ν，网络参数分别为θn和ω。策略网络μn根据观测on，t生成相应的动作an，t，价值网络ν则根据状态st对所有智能体的动作at进行打分，获得全局价值qt，如式（4）和式（5）所示。

MADDPG 算法是一种异策略算法，其训练过程分为探索和更新2 个部分。在探索过程中，智能体通过行为策略收集经验。行为策略通常是在当前策略网络输出的基础上加入随机噪声ξ，从而得到行为动作abeh，n，t，而噪声ξ服从均值为0、标准差为σ的高斯分布中随机抽取得到，如式（6）和式（7）所示。

经过1 次行为策略的探索，便会产生1 条经验，用六元组(st，ot，at，rt，st+1，ot+1)表示，并将其存入经验回放数组中。当数组存满后，使用新的交互数据代替最旧的记录。数组的大小是可调的超参数，其会影响训练的效果。使用经验回放可以打破序列的相关性，且可以重复利用历史经验，提高样本效率。

经过预热训练后，采用蒙特卡罗算法从经验回放数组中随机抽取小批量的样本，用样本均值代替期望，以此更新神经网络的参数。假设批量大小为B，其 中 第b（b=1，2，…，B）条 样 本 为(sb，ob，ab，rb，s′b，o′b)，sb、rb分别为更新过程中第b条样本的状态、奖励值，ob={on，b|n=1，2，…，N}为更新过程中第b条样本的观测，ab={an，b|n=1，2，…，N}为更新过程中第b条样本的动作，o′b={o′n，b|n=1，2，…，N}，上标“ ′ ”表示下一时刻的变量。

为了缓解自举和最大化造成的价值高估问题，还需要引入目标策略网络μn-和目标价值网络ν-，其网络架构与原网络相同，但参数分别变为θn-和ω-。

首先使用时间差分（temporal difference，TD）算法更新价值网络ν的参数ω。针对第b条样本，通过目标网络依次计算下一时刻的动作a′n，b-和价值q′b-，由此得到TD目标yb-，如式（8）—（10）所示。

通过价值网络计算当前的价值qb，并得到TD 误差λb，分别如式（11）和式（12）所示。

根据样本的TD误差λb，利用梯度下降更新价值网络参数ω，如式（13）所示。

式中：ην为价值网络的学习率。

然后使用策略梯度算法更新策略网络μn的参数θn。针对第b条样本，根据智能体n的观测on，b计算其动作a^n，b，再结合该样本中其他智能体的历史动作a1，b、a2，b、…、an-1，b、an+1，b、…、aN，b，得到动作价值q^n，b，如式（14）和式（15）所示。

根据链式法则计算策略梯度gn，b，再由B条样本的均值，利用梯度上升更新θn，见式（16）和式（17）。

式中：ημ为策略网络的学习率。

最后采用软更新算法更新目标策略网络和目标价值网络的参数θn-、ω-，分别如式（18）和式（19）所示。

式中：τ为软更新因子。

2.2 分解式价值网络

MADDPG 算法存在信用分配问题，其采用集中式价值网络对所有智能体的动作进行综合评价，但无法量化每个智能体对全局价值的贡献程度，因此可能会出现“懒惰智能体”。当部分智能体提前学习到较好的策略，对奖励有较大的提升时，某些智能体会失去探索的动力。所以集中式价值网络会造成最终策略陷入次优解，导致算法拓展性较差。针对上述问题，本文提出分解式价值网络的改进方法，将全局价值分解为每个智能体的个体价值，由此分辨每台光伏设备对系统整体电压控制的效用。VD-MADDPG算法的神经网络结构如图1所示。

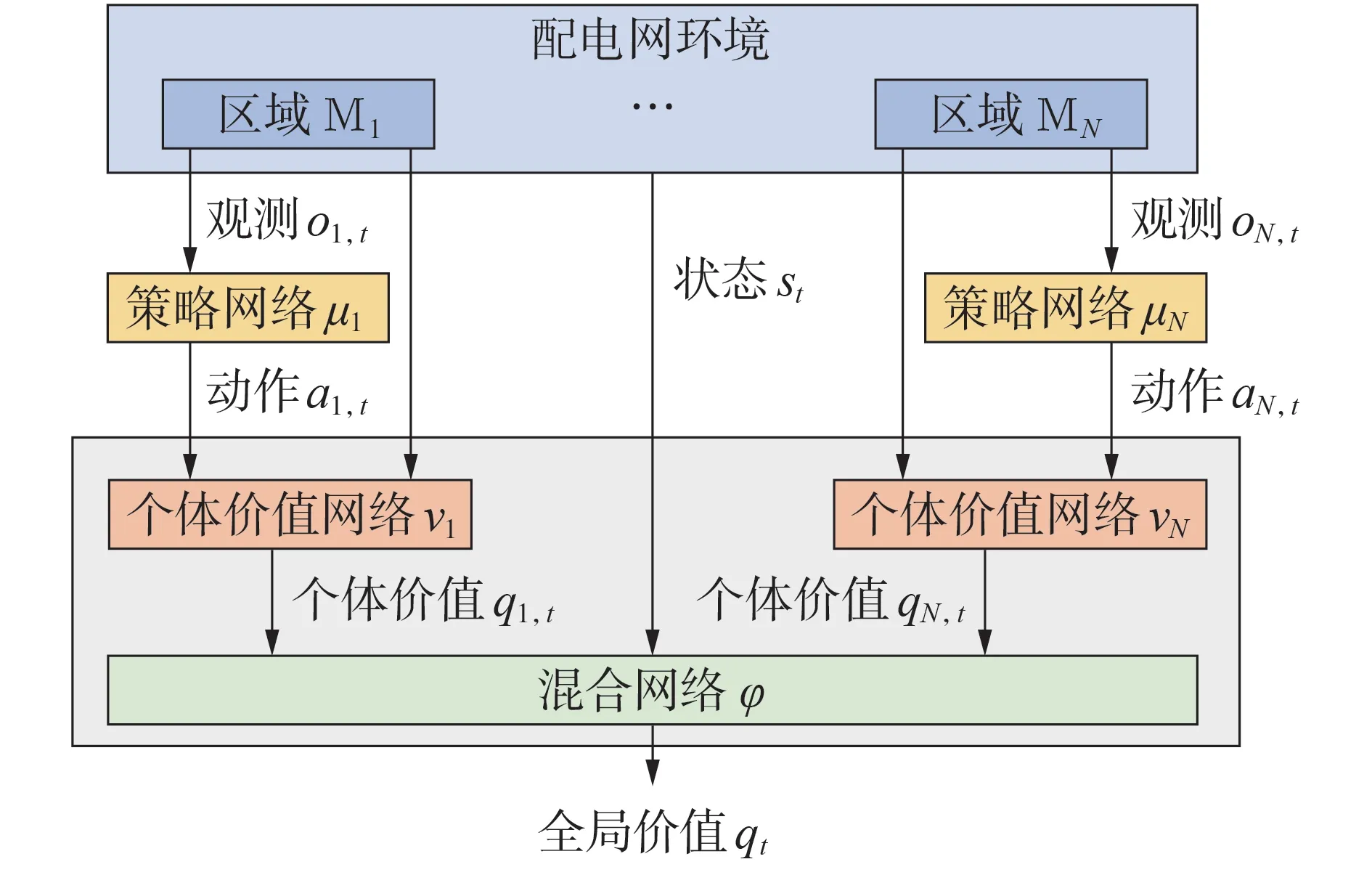
图1 VD-MADDPG算法的神经网络结构Fig.1 Neural network structure of VD-MADDPG algorithm

智能体n将自身的观测on，t和动作an，t输入个体价值网络νn中，其参数为ωn，由此得到个体价值qn，t，如式（20）所示。

然后将状态st和所有智能体的个体价值q1，t、q2，t、…、qN，t输入混合网络φ（其参数为χ）中，得到全局价值qt，如式（21）所示。

与MADDPG 算法类似，在训练过程中还需引入目标策略网络μn-、目标个体价值网络νn-和目标混合网络φ-，假设其参数分别为θn-、ωn-、χ-。

采用TD 算法更新个体价值网络νn和混合网络φ的参数ωn、χ。根据目标网络计算第b条样本对应下一时刻的动作a′n，b-、个体价值q′n，b-、全局价值q′b-，由此得到TD目标yb-，见式（22）—（25）。

将第b条样本中的动作an，b输入个体价值网络νn和混合网络φ中，得到当前时刻的个体价值qn，b和全局价值qb，再根据TD 目标yb-计算TD 误差λb，如式（26）—（28）所示。

根据所有样本的TD误差λb，利用梯度下降和链式法则更新参数ωn、χ，分别见式（29）和式（30）。

式中：ηφ为混合网络的学习率。

2.3 集中式策略梯度

当MADDPG 算法更新策略网络参数时，在式（15）所示动作价值q^n，b的计算过程中，只有智能体n的动作是根据当前策略网络μn计算得到的，而其他智能体均是从经验回放数组中抽取的历史动作，当前策略的动作选择存在较大的差异，因此容易导致策略网络的过度泛化。而在式（16）所示策略梯度gn，b的计算过程中，MADDPG算法针对每个智能体的策略进行单独更新，造成智能体之间的协调性较差，导致最终联合策略的性能表现欠佳。

因此，本文针对上述不足，提出集中式策略梯度的改进方法。根据当前的策略网络μn，计算每一个智能体的最新动作a^n，b，再通过个体价值网络νn和混合网络φ依次得到个体价值q^n，b和全局价值q^b，如式（31）—（33）所示。

假设所有策略网络的参数θ1、θ2、…、θN构成联合策略参数θ。求解全局价值q^b对联合策略参数θ的梯度gb，再利用梯度上升对所有智能体的策略网络进行集中更新，如式（34）和式（35）所示。

最后采用软更新算法更新目标策略网络μn-、目标个体价值网络νn-和目标混合网络φ-的参数θn-、ωn-、χ-，分别如式（36）—（38）所示。

2.4 VD-MADDPG算法的架构及流程

引入上述分解式价值网络和集中式策略梯度2 项改进措施后，本文提出了VD-MADDPG 算法。VD-MADDPG 算法的实现方式为中心化训练和去中心化执行（centralized training with decentralized execution，CTDE）架构［20］，即在配电网主站进行训练，在配电网边缘侧进行控制，其架构图如附录A图A2 所示。在中心化训练过程中，配电网主站收集全局信息，智能体之间可以共享观测、动作等数据，由此根据全局价值分数指导每个智能体改进自身策略。当训练结束后，配电网主站将策略网络的参数下发至各分布式光伏的边缘计算装置中，而不需要下发个体价值网络和混合网络的参数。去中心化执行过程在边缘侧完成，各分布式光伏只需要采集所在局部区域的节点特征信息，无须进行各装置之间的通信和数据共享，仅依靠自身策略网络的前馈运算便可以输出控制动作，执行速度达到毫秒级。使用CTDE 架构既可以学习到全局协调的控制策略，又能减少通信时延，节约通信成本，保证决策的实时性。VD-MADDPG算法的具体流程如附录B所示。

3 算例分析

3.1 算例设置

为了进行分布式光伏主动电压控制仿真测试，本文对IEEE 33 节点配电网系统进行改进，在节点12、17、21、24、28、32 处安装光伏，并将配电网划分为4个区域。系统的基准电压为12.66 kV，电压安全范围为［0.95，1.05］ p.u.。改进的IEEE 33 节点配电网系统拓扑如附录C图C1所示。

光伏及负荷数据来自华北电网某地区2020 —2022连续3 a的历史记录，数据时间间隔为5 min，与实时调度时间尺度一致。本文设置总控制周期为1 d，即1 个控制周期内包含288 个时间步。从总数据集中随机选取10 d 数据构成验证集，随机选取120 d数据构成测试集，其余数据则作为训练集。

为了验证本文所提算法的有效性，选取无控制、基于MADDPG算法、基于VD-MADDPG算法、基于集中式优化的4 种控制方法进行对比分析。其中：无控制方法表示将所有光伏逆变器的无功出力设置为0；基于MADDPG 算法、基于VD-MADDPG 算法的控制方法的优化目标一致，均为求解最优协调控制策略，使系统电压偏差、网络损耗最小，协调因子α=0.1；基于集中式优化的控制方法表示在全局网络参数已知的情况下得出理论最优解。本文根据经验列出超参数的典型取值范围，然后进行网格搜索确定各超参数的最佳取值。最终结果如下：神经网络隐藏层维度为64，经验回放数组的大小为5 000，样本批量大小为32，折扣率γ=0.99，行为策略中的噪声标准差σ=0.1，价值网络、策略网络、混合网络的学习率ην、ημ、ηφ均为0.001，目标网络的软更新因子τ=0.01。

3.2 训练结果

采用基于MADDPG 算法和基于VD-MADDPG算法的控制方法训练智能体，设置总训练回合数为400，每隔10 个回合进行1 次验证，计算其平均奖励值。选取5 个随机种子进行重复训练，观察训练过程的稳定性。同时对比无控制方法和基于集中式优化的控制方法的奖励值。奖励训练曲线见图2，图中阴影部分表示误差范围。

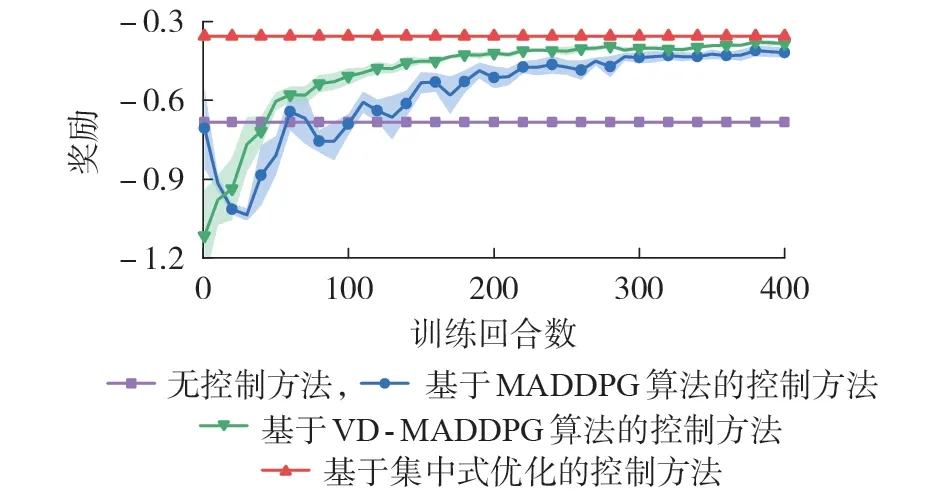
图2 奖励训练曲线Fig.2 Training curves of reward

由图2 可知，本文所提VD-MADDPG 算法在奖励大小、收敛速度、训练稳定性等方面均优于传统的MADDPG 算 法。MADDPG 算 法 和VD-MADDPG 算法在训练初期采用行为策略进行随机探索，控制效果较差，奖励值甚至低于无控制时的表现。随着训练回合数的增加，智能体不断地积累经验，并逐渐学习到更优的控制策略，奖励曲线随之增大直至收敛。无控制方法和基于集中式优化的控制方法的平均奖励分别为-0.682 8、-0.354 6，基于MADDPG 算法和基于VD-MADDPG 算法的控制方法分别在第300 个回合和第200 个回合左右收敛，最终奖励值分别为-0.417 7、-0.384 7，相比于无控制方法分别提升了38.83 %、43.66 %。相比基于MADDPG 算法的控制方法，基于VD-MADDPG 算法的控制方法的收敛值更加接近理论最优值，且误差范围更窄，波动性更小，具有更好的训练稳定性，由此验证了本文所提VD-MADDPG 算法的优越性。VD-MADDPG 算法采用了分解式价值网络和集中式策略梯度2 项改进方法，因此能够评价每台光伏对系统电压控制的贡献程度，避免出现“懒惰智能体”，并且对所有智能体的策略进行协同更新，能够保证学习到全局最优的联合策略，进一步提升了算法的训练效果。

3.3 测试集结果

将上述训练好的策略模型应用于测试集上进行测试，对比4 种方法的控制性能。测试指标包括电压偏差、网络损耗、计算时间。此外，为了从时空的不同角度进一步刻画电压控制效果，本文还引入电压越限率、完全控制率2 项指标。电压越限率是指电压超过安全范围的节点的数量比例，完全控制率是指将所有节点的电压控制在安全范围内的时间占比。测试集结果见表1，表中电压偏差为标幺值。

表1 测试集结果Table 1 Results of test set

由表1可知，相较于MADDPG算法，VD-MADDPG算法在测试集上取得了更好的稳压减损控制效果。当不对配电网中的分布式光伏进行控制时，系统电压存在较大的偏差，平均有4.75 % 的节点发生电压越限，仅有78.46 % 的时间能保证所有节点的电压均处于安全范围内。无控制时光伏逆变器的无功出力为0，潮流在节点间的流动较少，因此线路上的功率损耗较小。当采用基于MADDPG 算法、基于VD-MADDPG算法的控制方法后，电压波动得到了明显平抑，电压偏差分别降低了46.87 %、58.88 %，电压越限率分别减少了88.84 %、99.16 %，完全控制率分别提升了13.97 %、26.51 %，这验证了使用分布式光伏进行主动电压控制的有效性。而相较于MADDPG算法，VD-MADDPG 算法的稳压性能更优异，仅有0.04 % 的节点发生电压越限，配电网在99.26 % 的时间内可安全稳定运行。虽然使用光伏逆变器输出无功后，会增加系统的有功损耗，但VD-MADDPG 算法可在实现优异的稳压效果的基础上，保持较小的网络损耗，其网损值为MADDPG 算法结果的33.87 %。此外，VD-MADDPG 算法的电压偏差、电压越限率、完全控制率、网络损耗的标准差分别为MADDPG 算法结果的79.77 %、22.62 %、23.93 %、70.31 %，这表明VD-MADDPG 算法在面对不同的复杂场景时，具有更好的鲁棒性、泛化能力。上述结果验证了本文所提算法的优越性，通过使用分解式价值网络和集中式策略梯度可大幅提升算法的性能表现。

虽然VD-MADDPG 算法的测试结果无法达到理论最优值，但集中式优化方法需要依赖于复杂的量测装置和完善的通信设施，建设成本过高，而VD-MADDPG 算法能从历史经验中学习到有效的协调策略，通过分布式控制达到近似最优的稳压减损效果，因此更加适用于低感知度配电网。此外，从表1 中还可看出，MADDPG、VD-MADDPG 算法仅需1 ms 左右的时间便可完成决策，远小于优化求解所需时间。这是因为MADDPG、VD-MADDPG 算法在执行过程中只需进行策略网络的前馈运算，因此具有极高的时效性，可充分满足在线应用的要求。MADDPG 和VD-MADDPG 算法的策略网络结构相同，仅网络参数存在差异，因此计算时间基本一致。

3.4 典型日测试结果

为了验证本文所提方法在高光伏渗透率情况下的鲁棒性和泛化能力，从测试集中选取光伏渗透率为250%的典型日场景进行测试，其光伏及负荷曲线如附录C 图C2 所示。由图可知，光伏出力和负荷需求分别在13:15、20:00左右达到最大值。

在该典型日场景下，分别使用无控制、基于MADDPG算法、基于VD-MADDPG算法、基于集中式优化的4 种方法进行控制。节点17 位于线路末端，且安装有大容量光伏，因此将节点17 作为代表性节点，对比4 种控制方法下的电压（标幺值）曲线，并观察系统网络损耗的变化情况，分别见图3和图4。

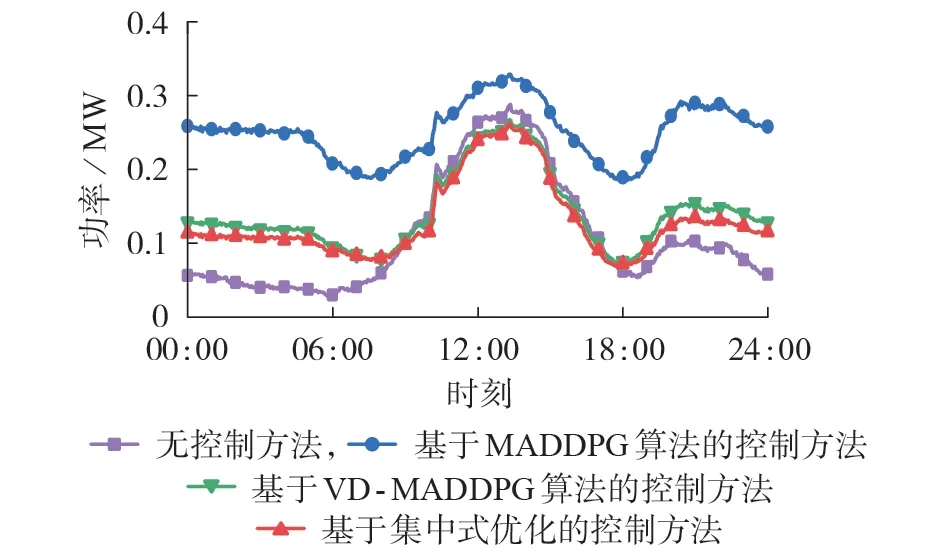
图4 典型日的网络损耗曲线Fig.4 Network loss curves on typical day

由图3可看出，相较于传统MADDPG 算法，本文所提VD-MADDPG 算法取得了更好的稳压效果。当不对电压进行控制时，节点电压在11:30 — 14:45 时段超过安全上限，在19:30 — 22:45 时段低于安全下限，节点电压偏差的平均值为0.037 p.u.，电压波动剧烈，电能质量很差。当采用MADDPG 算法进行控制时，节点电压整体抬升，虽然保证了夜晚时段的电压安全，但在正午时段电压越限的严重程度反而加重了，电压偏差高达0.042 p.u.。而采用本文所提VD-MADDPG 算法进行改进后，节点电压在整个典型日均处于安全范围之内，电压偏差降为0.019 p.u.，相比MADDPG 算法的结果减少了54.76 %，说明VD-MADDPG 算法能够学习到更好的控制策略，实现多台光伏设备的有效协调，解决了电压越限问题。集中式优化虽然能够给出理论最优解，电压偏差达到最小值0.017 p.u.，但该方法需要依赖于精确的网络参数，且求解速度缓慢，难以进行在线部署。而VD-MADDPG 算法能够从历史交互数据中学习到近似最优的控制策略，其电压曲线与集中式优化方法得到的电压曲线十分接近，在正午时段几乎重合，并且可以进行实时决策，能够充分满足实际调度需要，这验证了本文所提VD-MADDPG算法的优越性。

由图4可看出，4种控制方法下的全天平均网络损耗分别为0.110 4、0.251 0、0.141 2、0.130 5 MW。无控制时的功率流动最少，因此网络损耗最小。相比于MADDPG 算法，采用VD-MADDPG 算法时网络损耗减少了43.75 %，能够在保证电压安全稳定的同时，将功率损耗维持在较小的水平，仅略高于集中式优化方法的结果。这进一步验证了本文所提VD-MADDPG算法在主动电压控制问题上的优越性。

为了进一步验证VD-MADDPG 算法对各智能体的动作改进效果，将光伏出力最大的13:15时刻作为代表性时刻，展示基于MADDPG 算法、VD-MADDPG算法、集中式优化这3种控制方法下6台光伏逆变器PV1—PV6的无功功率动作，结果如图5所示。

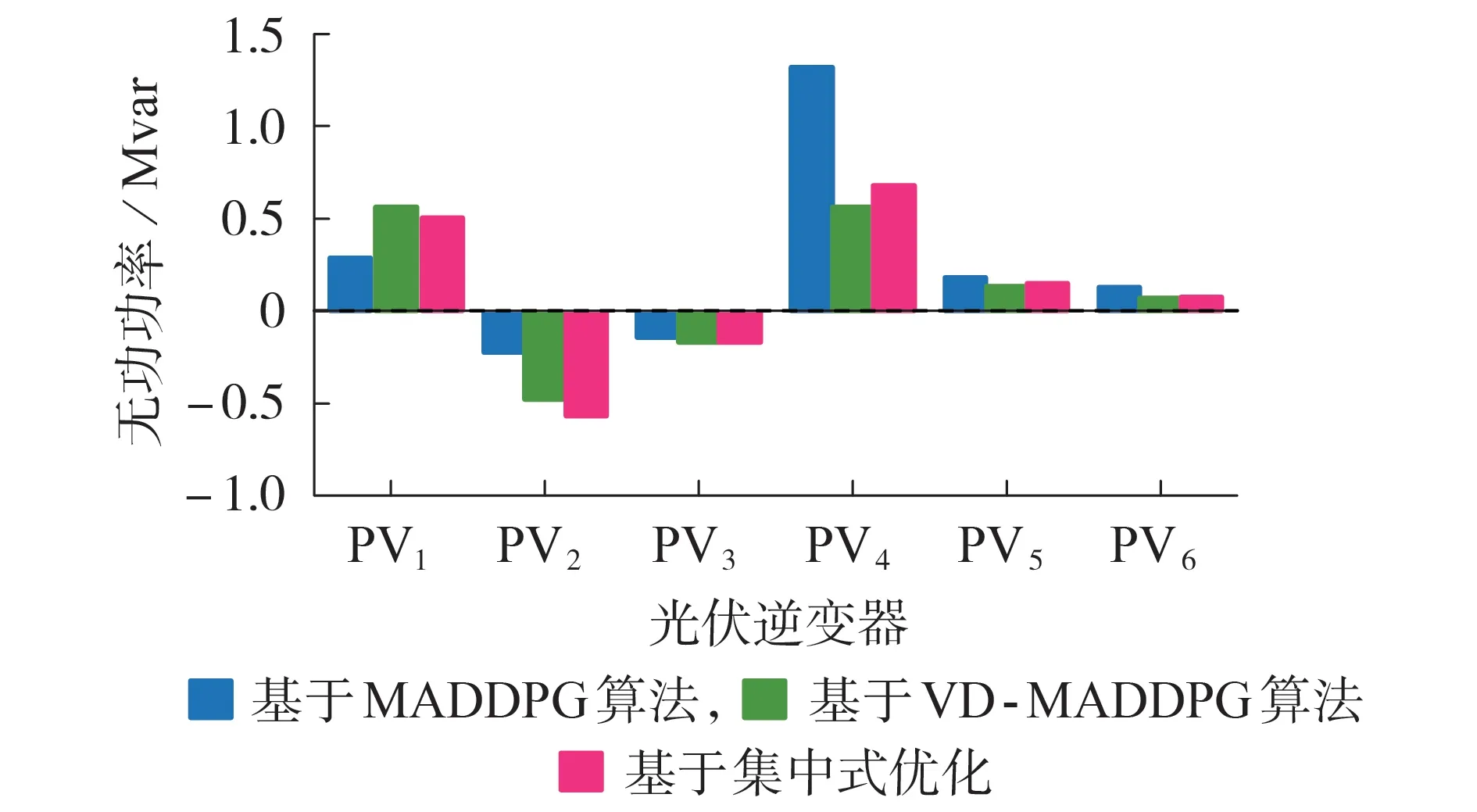
图5 光伏逆变器的无功功率动作Fig.5 Reactive power action of photovoltaic inverters

集中式优化方法能给出理论上的最优解，因此可将该方法下的光伏逆变器无功出力作为最优动作基准。由图5 可知，当采用VD-MADDPG 算法改进后，6 台光伏逆变器的无功出力均变得更好，与最优动作基准的差距变小。当采用MADDPG 算法时，各光伏逆变器的无功出力与最优动作基准的相对最大差距为94.24 %，相对差距最大的“懒惰智能体”为PV4。由于懒惰现象的存在，各光伏逆变器间无法做到有效协调，控制策略陷入次优解，难以解决电压越限问题。而采用VD-MADDPG 算法后，PV4的相对动作差距降为17.50 %，其他光伏逆变器的动作差距也均得到降低。这说明采用价值分解进行算法改进后，每个智能体都有相应的个体价值网络对自身动作进行打分，评价其对全局价值的贡献，以此督促每个智能体进行经验探索和策略学习，避免出现“懒惰智能体”，更好地实现了智能体间的协调合作。

4 结论

由于存在信用分配、过度泛化等问题，传统MADDPG 算法在进行分布式光伏主动电压控制时，性能表现欠佳。为此，本文提出了一种基于价值分解的改进VD-MADDPG 算法用于分布式光伏主动电压控制。首先，将该问题建模为Dec-POMDP；然后，在CTDE架构的基础上，提出了分解式价值网络和集中式策略梯度2 项改进措施，将全局价值网络分解为个体价值网络和混合网络，以此评价每个智能体对全局价值的贡献程度，并采用所有智能体的当前策略进行集中参数更新，以此训练得到更加协调的联合控制策略。改进的IEEE 33 节点配电网系统的算例结果表明，相比于传统MADDPG 算法，VD-MADDPG算法能够有效地平抑电压波动，缓解电压越限，降低网络损耗，具有更加优越的稳压减损控制效果。同时，VD-MADDPG 算法的收敛速度更快，训练过程更稳定，针对复杂场景的鲁棒性更强。

本文所提方法同样适用于电动汽车、储能、智能软开关等可连续调节的电力电子设备，具有可拓展性。进一步考虑上述设备在主动电压控制问题中的精细化建模，实现多种灵活性资源的有效协调，是笔者后续的研究方向。

附录见本刊网络版（http：//www.epae.cn）。