分时电价下居民用户用电需求响应估计方法
2023-11-11李昭昱
李昭昱,艾 芊
(上海交通大学 电子信息与电气工程学院 电力传输与功率变换控制教育部重点实验室,上海 200240)
0 引言
随着“双碳”目标与新型电力系统建设的持续推进,新能源的占比不断提高,对电网灵活性提出了更高的要求[1]。需求响应(demand response,DR)通过合理调动需求侧资源,可以减轻对新增发电设备的需求,实现能源的优化利用及提升电力系统灵活性[2-3]。据统计数据分析,DR 有助于减少10 %~30 %的高峰负荷,其中居民用户占DR 潜力的40 %~60 %[4],因此近年来针对居民用户的DR 研究受到广泛重视。
在挖掘居民负荷的DR 潜力时,为了避免直接负荷控制对用户隐私的侵犯,通常实施基于价格的需求响应(price-based demand response,PBDR),通过电价信号反映供求关系,对用户用电行为进行引导[5]。对用户的响应情况进行估计是实施PBDR 的重要前提[6],其中的一类代表性研究为通过统计指标实现DR 估计[7-9],此类统计指标通过对参与DR 用户进行排序及分类,可以作为DR 用户筛选的依据,但难以反映施加价格信号时,用户根据价格调整用电量的具体情况。
目前,针对居民用户参与PRDR 的响应量定量估计已开展了部分研究。文献[10]将DR 用户划分为3 类用户,通过具体分析每个类型负荷用户的不确定性来源,构建各类用户的响应量期望模型。在进行用户分析时,需要明确参与PBDR 用户的负荷构成,并确定其DR 的深度及设备的状态。文献[11]提出计及响应不确定性的居民温控负荷响应量评估方法,实现用户响应潜力评估及其分布特性计算。其中,指标数据计算对于用户信息掌握的需求较高,主要适用于已参与PBDR 用户的存量资源评估,而未参加PBDR 的用户由于缺乏历史响应数据,难以实现精准的响应量估计。此外,需明确的是,对未参加PBDR 用户的用电响应估计问题与一般的负荷预测问题也存在差异,主要表现为:后者针对未来的用电量进行预判,而前者则是针对未参加PBDR用户,在假设给予的电价激励下,对可能的DR 情况进行估计。因此,PBDR 发生日的全天负荷量为已知量测信息。此外,相较于负荷预测问题,对未参加PBDR 用户的用电响应情况进行估计存在以下难题:①负荷预测问题一般针对未来固定周期负荷进行预测,而DR 发生的时段和持续时间的长短均不固定,为估计带来较大的困难[12];②未参加PBDR 用户自身的用电信息无法反映DR 的情况,需要合理选择与其真实响应情况具有较大相似性的输入特征,以实现对其DR量的估计。
为了解决缺少历史响应数据支撑的用户DR 量估计问题,部分文献采用已有响应数据的相似用户进行辅助估计。文献[13]提出基于高斯混合模型的DR估计模型,选取历史日中典型负荷曲线相似的用户数据用于高斯混合模型的训练,但是未明确价格信号与DR 潜力间的关联。文献[14]提出用户DR潜力评估的数据迁移学习框架,实现基于源域用户数据的目标域用户的响应潜力估计,但未对DR 发生日的响应时段和非响应时段进行划分,未实现对数据的充分利用。因此,本文旨在利用参加PBDR用户用电量以及未参加PBDR 用户非峰/谷时段用电量信息,构建合适的模型结构,以解决上述的难题。
支持向量机回归(support vector regression,SVR)作为机器学习领域的重要算法,在不同领域的参数估计、时间序列分析和预测中表现优异[15]。SVR 基于结构风险最小化原则,在小样本问题方面展现出独特的优势,且具有良好的泛化能力[16]。因此,针对分时电价激励下,未参加PBDR 用户的潜在响应量量化估计问题,本文提出一种基于SVR 模型的居民用户用电DR 估计方法。首先,构建未参加PBDR 用户的输入特征,通过寻找已参加与未参加PBDR 用户间用电行为的相似性,为各未参加PBDR用户DR 发生日的每个峰/谷时段选择合适的输入特征,同时为应对PBDR 发生时段和持续时间的不确定性,将待估计时段表示为哑变量;随后,基于SVR 模型建立输入输出之间的映射关系,对各用户DR 发生日每个峰/谷时段PBDR 响应情况进行估计;最后,进一步计算用户用电的需求弹性指标,实现用户对价格信号的敏感度的整体定量评估。实验分析表明,本文所提基于SVR 的模型相较于采用单一统计指标可以实现响应情况的精细化估计,且估计效果优于基于相似日的方法。
1 基于SVR的居民用户用电DR估计
本文所提方法流程图如图1 所示,主要包括数据预处理、输入特征构建、模型构建和需求弹性估计4个步骤。
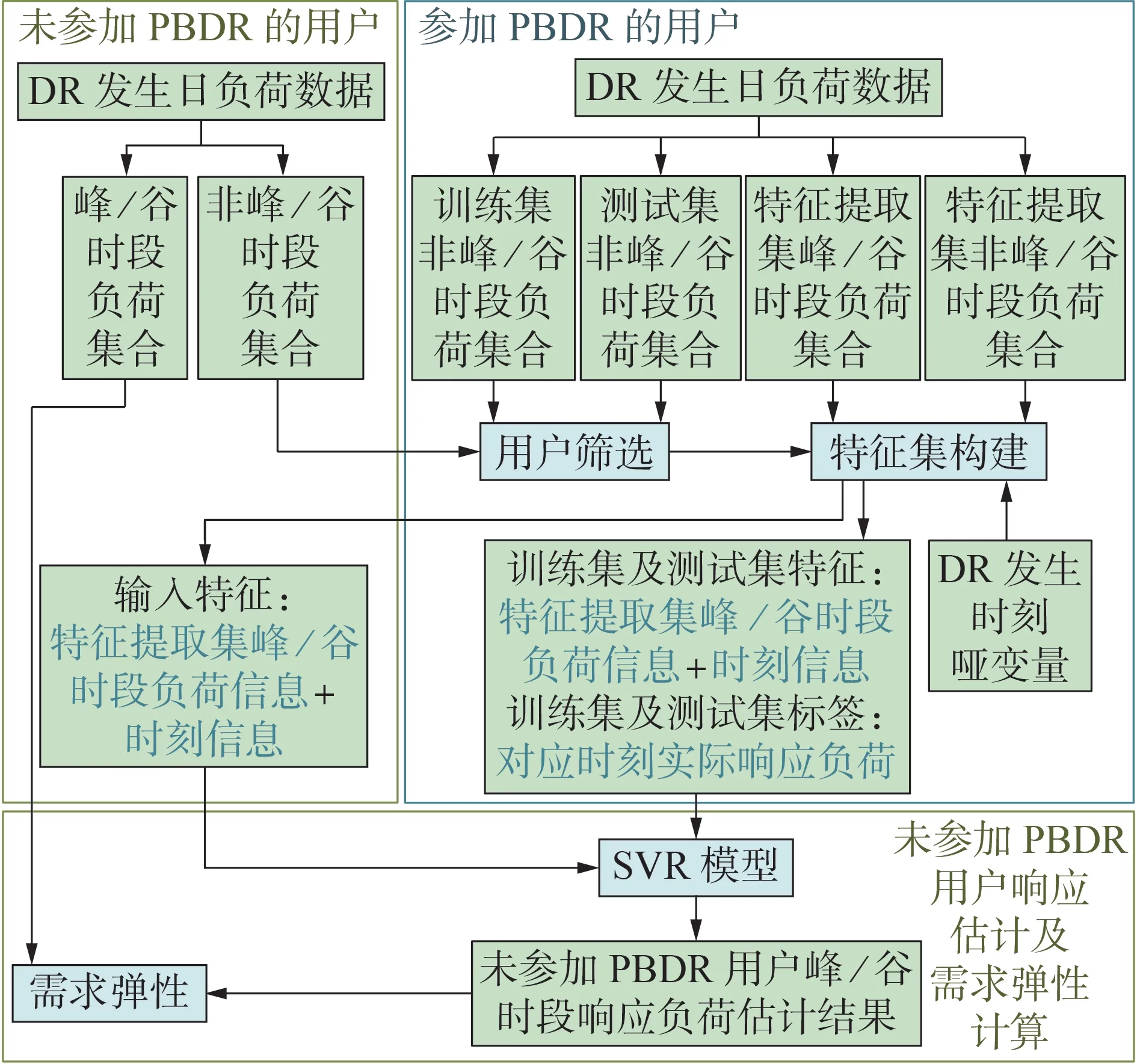
图1 所提方法流程图Fig.1 Flowchart of proposed method
1.1 数据预处理
假设用户一天内量测点的个数为Tm,则用户i第j天的负荷量可表示为di,j∈R1×Tm,其中j∈ΩE,ΩE为PBDR 发生日的集合。为避免幅值对用户相似性特征判断的影响,首先对用户的负荷量进行归一化,将其归一化至[0,1]区间:
后续的步骤均依据归一化后的数据进行。由于无法得知未参加PBDR 用户在电价信号下的实际响应量,为评估所提估计方法的准确性,模型的训练和测试均基于参加PBDR 的用户数据。因此,按照50 %、25 %、25 % 的总样本将参加PBDR 的用户划分为特征构建集、训练集、测试集,待模型训练完成后,在测试集上进行估计准确度的评估,并针对未参加PBDR用户进行响应量和需求弹性的估计。
1.2 输入特征选择
针对每个未参加PBDR 的用户、训练集和测试集中参加PBDR 的用户,在每天各峰/谷时段分别构建输入特征集。由于用电曲线类似的用户很大程度上具有相似的生活习惯以及用电规律,对电价信号会有类似的用电响应[12],因此本文根据非峰/谷电价期间用电量,筛选出与目标用户用电规律较相似的参加PBDR 的用户,并将其峰/谷电价期间的用电量作为目标用户的部分输入特征[17],同时,为应对PBDR发生的不同时段,采用哑变量对PBDR发生时段进行标注。
特征筛选过程具体由以下几个步骤组成。
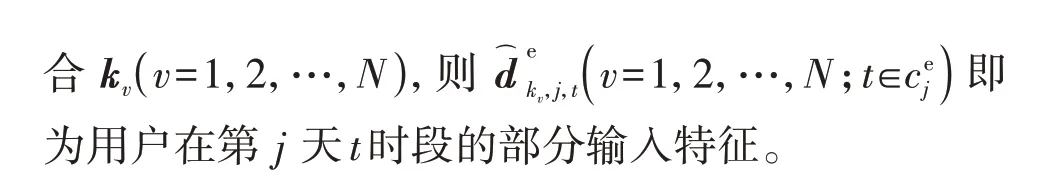
3)针对不同时段的响应量差异,采用哑变量对PBDR 发生时段进行标注,并将对响应时段的估计转化为点估计,以解决PBDR 发生时段和持续时间不固定的难题。具体为:将用户i第j天的哑变量记为pi,j∈R1×Tm,当t时段发生PBDR 事件时,哑变量中的元素pi,j,t=1,反之pi,j,t=0。
1.3 回归模型训练
本文采用基于径向基核函数的SVR[18]进行负荷DR量的评估。模型的输出即为估计得到的用户i在第j(j∈ΩE)天t(t∈cej)时段的响应量。根据上文得到的输入特征xi,j,t,将峰/谷电价时段参加PBDR 用户的实际负荷值作为模型标签,在训练集和测试集上进行SVR 的训练与评估。其中SVR 的训练过程可以表示为如下的优化问题:
式中:w、b、ξ、ξ*为决策变量;m为样本数目;ξi、ξi*分别为ξ、ξ*中的元素;xi、yi分别为输入特征和对应的标签值;C、ε表示控制对预测误差的松弛程度;φ(xi)表示对输入特征xi进行高维映射,其对应的核函数可以表示为
1.4 需求弹性估计
在SVR 训练结束后,根据未参加PBDR 用户的输入特征,对电价信号下的用电需求进行估计,并进行需求弹性的计算。对于未参加PBDR 的用户i,其在第j天t时段的需求弹性Ei,j,t可由如下公式进行计算:
2 居民用户用电DR估计效果对比
下面选取平均绝对百分比误差(mean absolute percentage error,MAPE)和均方根误差(root mean square error,RMSE)作为评判各种方法估计效果的依据[19],其值越小表示估计效果越好。并提出居民用户用电DR 估计效果对比的4种方法。其中,方法1 和方法2 均采用本文所提出的方法,但针对)采用不同的距离度量方法,方法3 和方法4均基于相似日法[20],具体分别如下。
1)方法1:本文所提出的方法+欧氏距离。基于所提出的方法,采用欧氏距离对)进行度量,即:
2)方法2:本文所提出的方法+互相关系数。基于所提出的方法,采用互相关系数Mcov(·,·)对距离进行度量,即:
3)方法3:对于用户i,获得欧氏距离下较小的3 个参加PBDR 的用户,将其构成的集合kv(v=1,2,3)作为返回量,在第j天t时段的响应量的平均值即为估计值,即:
4)方法4:基于文献[20]提出的方法,对于估计用户i在第j天t时段的响应量,根据该时段分时电价类型(峰值/谷值),采用相同电价类型相同时段下最近3 d 的响应量的平均值作为该时段响应负荷的估计。值得注意的是,由于未参加PBDR 的用户没有接受电价信号,因此该方法不适用于此类用户,方法4 仅用于对测试集参加PBDR 用户响应量估计的比较。
3 算例分析
下面首先对所采用的数据进行描述,随后对所提特征筛选效果进行分析,其次基于由参加PBDR用户构成的测试集,进行各个估计方法的比较,并对特征选择个数进行分析。最后,针对未参加PBDR的用户,采用本文提出的估计方法得出其估计响应量,并与其基准负荷进行对比,从而计算出需求弹性。需注意的是,由于无法获得未参加PBDR 用户关于电价的真实响应量,为定量进行方法的评估,本文基于由参加PBDR 用户构成的测试集,计算估计响应量和真实响应量间的偏差,从而进行定量比较。
3.1 数据描述
本文的数据是基于Low Carbon London 实验[21]提供的每隔半小时记录一次的智能电表数据,因此全天共有48 个量测点。按照接受电价的不同,Low Carbon London 实验用户可以分为接受固定电价以及接受分时电价的用户。其中,固定电价为0.142 28 £/(kW·h);分时电价分为峰、平、谷3 个时段,分别取0.672 0、0.117 6、0.039 9 £/(kW·h)。本文随机选取接受分时电价的251 个用户,以及接受固定电价的100个用户2013年全年的用电量进行分析。则对于参加PBDR 的用户,特征构建集包括125 个用户,训练集和测试集各包括63 个用户。各用户全年有2 064 个时段参与DR,因此训练集和测试集样本大小均为130 032(63×2 064),未参加PBDR用户样本大小为206 400(100×2 064)。
3.2 特征筛选效果分析
为直观展示所提特征筛选方法的有效性,在部分输入特征个数N=20 的情况下,选取未参加PBDR的任意一个用户,将其非峰/谷时段的用电行为与特征构建集中筛选得到的相应用户用电规律进行比较,以2013-07-25 的结果为例,其结果如图2 所示,选取其余3 d 的对比结果如附录A 图A1 所示,图中负荷为标幺值,后同。可以看出,特征构建集中所筛选出来的用户用电行为与未参加PBDR 用户具有较大的相似性。图2中,未参加PBDR用户用电呈现出2 个尖峰时段,筛选出来的用户可以很好地把握此用电规律。故本文所提方法可以对相似用户进行有效筛选。
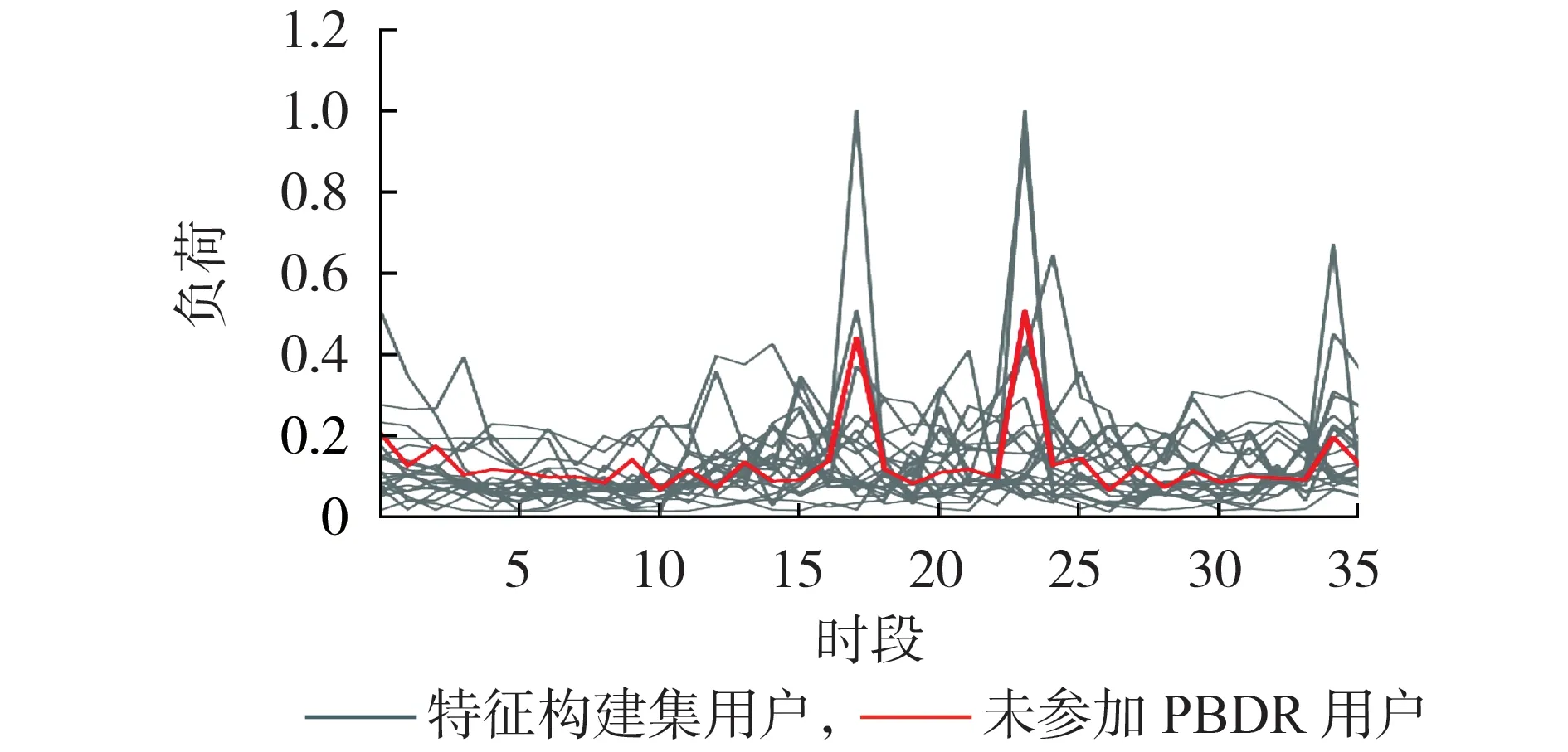
图2 未参加PBDR用户与特征构建集用户非峰/谷时段负荷比较Fig.2 Comparison of load between non-PBDR customers and customers in feature construction set during non-peak/valley periods
此外,针对不同响应持续时间,将筛选得到的特征构建集中用户与构成测试集中任一参加PBDR 用户用电响应情况进行对比,如图3 所示。筛选得到用户响应情况与真实响应情况具有以下2 类相似性:①用电水平相似,在图3(a)中,大部分特征构建集用户与目标用户在电价激励下用电水平几乎相同;②用电趋势相似,在图3(b)中,筛选得到的特征构建集用户与目标用户对电价具有类似的响应趋势,其中筛选出来的大部分用户在0 — 5时段用电量较小,随后快速上升。此外,附录A 图A2 展示了另外2 种用电趋势的情况。可见图A2(a)中大部分特征构建集用户用电呈现锯齿状波动,图A2(b)中筛选出来的大部分用户也同样具有用电量下降趋势。
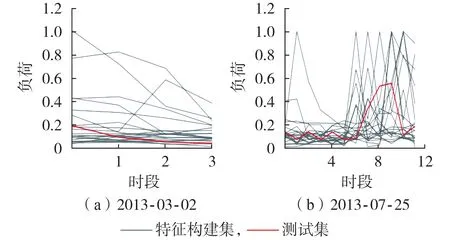
图3 测试集与特征构建集用户峰/谷时段负荷比较Fig.3 Comparison of load between customers in test set and customers in feature construction set during peak/valley periods
此外,为进一步证明测试集中的用户与筛选得到特征构建集中用户在响应时段具有类似的用电规律,采用互相关系数(定义如式(6)所示)对用电曲线之间的相关性进行定量衡量,其直方图如图4 所示。可以看出,相关系数的分布集中在[0.6,1.0]之间,表明相关性较大。
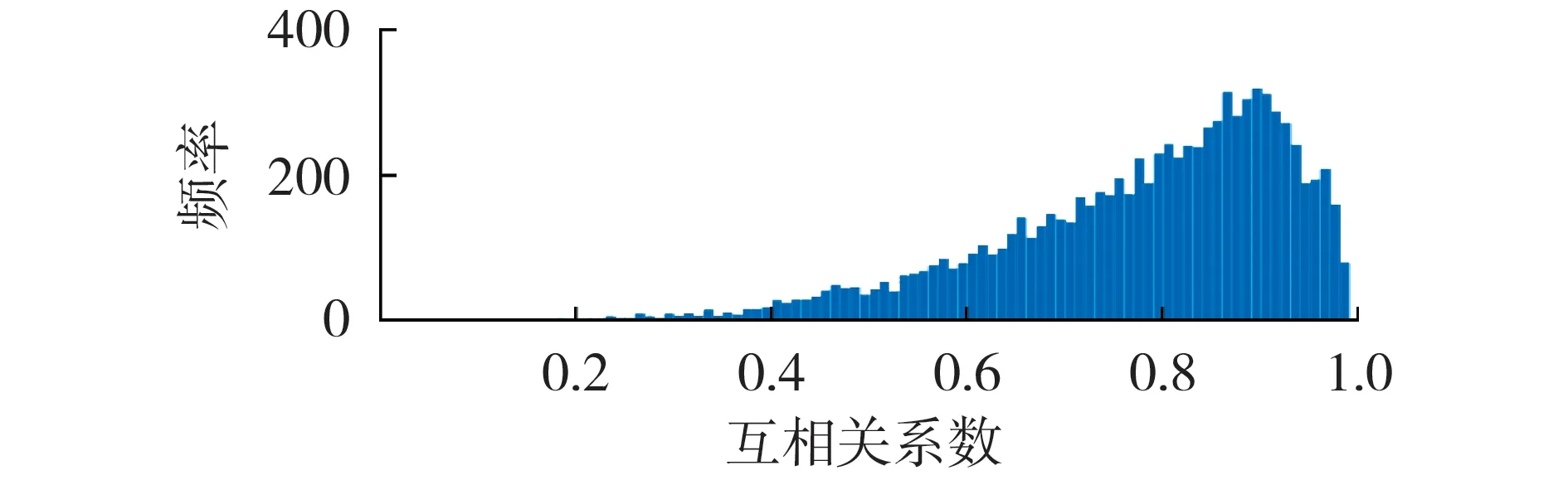
图4 测试集与特征构建集用户用电曲线间互相关系数分布直方图Fig.4 Histogram of cross-correlation coefficient between load profiles of customers in test set and feature construction set
值得注意的是,本文仅基于非峰/谷时段筛选得到特征构建集中用户,而在峰/谷电价发生时,筛选用户与目标用户具有类似的响应情况,证明了所提特征筛选方法的有效性。
3.3 用电响应估计准确性分析
第2 章中4 种方法在测试集上估计效果的评价指标如表1 所示,表中方法1 和方法2 的部分输入特征个数N=20。由表可见,方法1 在RMSE 和MAPE统计指标方面均优于方法2,因此与互相关系数相比,欧氏距离更适合于评估用户曲线的相似性。此外,与基于相似日的方法3 和方法4 相比,方法1 展现出更好的估计效果,表明所提基于回归模型的方法优于基于相似日的方法。
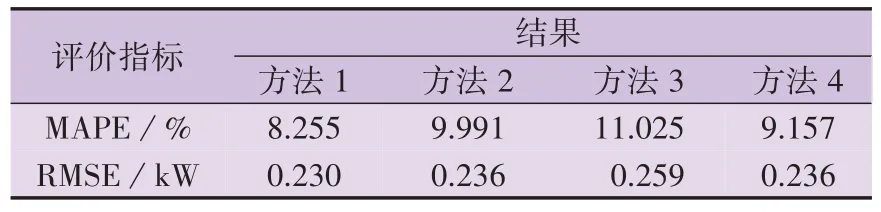
表1 对测试集上DR估计准确度的比较Table 1 Comparison of DR estimation accuracy on test set
方法1、方法3 和方法4 在峰值电价和谷值电价阶段的预测效果如表2 所示。在2013 年全年中,有71 d 存在峰值电价阶段,96 d 存在谷值电价阶段。对于3 种方法,谷值电价阶段的预测误差均大于峰值电价阶段。在峰值电价阶段,用户收到高电价信息,减少电器的使用,因此负荷的随机性减小,使得估计更为准确,而谷值电价阶段情况正好与之相反。在这3种方法中,方法1在峰值阶段和谷值阶段均取得最好的效果。
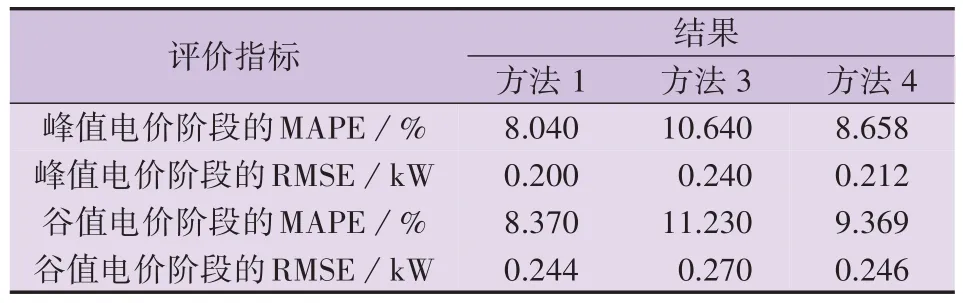
表2 对测试集上峰/谷电价时段DR估计准确度的比较Table 2 Comparison of DR estimation accuracy on test set during peak/valley price periods
从测试集中随机选择用户的实际响应负荷与估计负荷情况进行对比,如图5 所示,其分别展示了峰值电价阶段(橙色阴影部分)与谷值电价阶段(紫色阴影部分),PBDR 在不同起始与持续时间的负荷情况。将方法1与方法3进行对比,可以看出智能电表数据具有较大的波动性,其给准确估计造成困难,但方法1 可实现负荷较为准确的估计。尽管采用方法3 可实现对负荷变化趋势的把握,但是在负荷波动较大时,估计偏差较大。
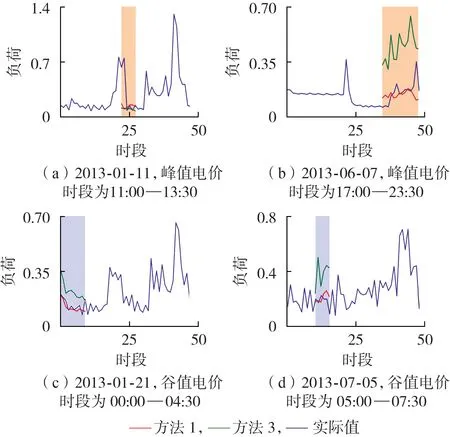
图5 由方法1、方法3估计响应负荷与测试集上实际响应负荷情况比较Fig.5 Comparison between estimated response load by Approach 1 and Approach 3 and actual response load on test set
3.4 特征个数N的选择
基于方法1,对N取值为20、50、80、110这4种情况进行实验,相应的评价指标如图6 所示。由图可知,随着特征个数N的增大,训练集上MAPE 与RMSE 指标均下降,这表明估计效果更为准确,但是测试集上MAPE 增大,这说明特征个数N的增大导致模型存在过拟合的问题。因此本文选取N=20。值得注意的是,尽管当N=110时,测试集RMSE达到最小,但其训练以及测试的总时间为3 h 25 min,而当N=20时,其训练以及测试的总时间为1 h 16 min,因此综合考虑估计准确度和计算效率,N=20为更好的选择。
3.5 未参加PBDR用户需求弹性评估
根据式(4),对未参加PBDR 用户的需求弹性进行评估,其直方图如图7 所示。从图中可以看出,大部分用户的需求弹性在[-1,0]之间,但也有部分用户需求弹性绝对值大于1,这表明该类用户用电需求的相对变化大于电价的相对变化,用户需求弹性较大,适合参加PBDR 项目。因此,通过计算需求弹性指标,可以发现适合参加PBDR项目的用户。
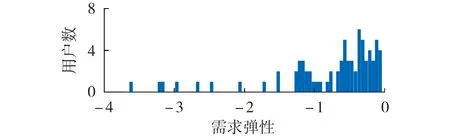
图7 需求弹性直方图Fig.7 Histogram of demand elasticity
4 结论
本文提出一种分时电价下未参与DR 的居民用户的用电响应量及需求弹性估计方法。该方法主要基于参加与未参加PBDR 用户用电行为的相似性,通过SVR 实现未参加PBDR 用户的响应量化估计,并进行需求弹性系数的计算,实验结果表明:
1)采用欧氏距离进行用电曲线相似度的衡量可以有效筛选出用电行为相似的用户,从而获得更高的估计准确度,且根据MAPE 和RMSE 评价指标,所提方法优于相似日法,同时对于峰值时段响应的估计比谷值时段更为准确;
2)在进行响应量估计时,不合理的特征个数设置可能会导致模型过拟合,影响其在测试集上的表现效果,因此需要对特征个数进行合理选择,以兼顾估计准确度和计算效率;
3)未参加PBDR 用户的需求弹性评估结果中,部分用户需求弹性绝对值大于1,该类用户用电需求对价格较为敏感,因此可以通过计算需求弹性,发现适合参加PBDR项目的用户。
附录见本刊网络版(http://www.epae.cn)。
