基于模量行波差异的柔性直流输电线路单端量保护方法

贾 科，姚昆鹏，刘子奕，刘可歆，张恬昕，毕天姝

（华北电力大学 新能源电力系统国家重点实验室，北京 102206）

0 引言

柔性直流输电技术具有可控能力强、电能质量高、运行方式灵活等优势［1-2］，是新能源基地远距离外送并网的重要手段之一。然而受全控型器件通流能力和系统低阻尼特性的影响［3］，柔性直流输电系统故障电流上升速度快，对保护的速动性要求高。为避免双端量保护通信延时、中断等因素的影响，单端量行波保护成为加快保护速度的有效手段［4］。

目前在直流工程投运的单端量行波保护中，利用电压突变量构成的保护在发生高阻接地故障时存在灵敏度较低的问题［5-6］，保护动作性能有待提高。为解决这一问题，众多学者开展了保护新原理的研究。一类保护新原理基于线路边界元件构成的“低通滤波器”对区外高频分量具有良好的衰减效果［7］，并配合小波变换［8］、数学形态学［9］等一系列信号处理手段，从而实现对区内外故障的有效识别。但上述保护的优良性能本质上仍无法避开提取行波突变量的过程，保护耐受过渡电阻能力受限于采样频率［10］，且所用算法可能存在计算时间长、时频处理复杂等问题；另一类保护新原理则从直流输电线路故障暂态特征解析出发［11-12］，基于限流电抗器电压差异［13］、行波峰值时间［14］、波前陡度［15］、波形拟合［16］等不同的角度构成故障识别判据并实现对线路故障的判别。现阶段研究认为这类保护中基于波形特征的新原理具有较强的耐受过渡电阻能力。然而在近端或对近端故障下，由于后续行波的快速到达，基于波形特征的保护新原理可能失效，保护范围存在死区。此外因复合模域故障等效电路的不同，区内、外故障下故障处电压波形将有所差异：区内故障与区外金属性故障下故障处电压为近似阶跃波，而区外非金属性故障下为近似指数上升波。若保护原理以区内、外故障下故障处电压均为近似阶跃波开展研究，则势必会对保护性能产生影响，甚至会影响系统安全。因此如何正确解析直流输电线路故障暂态特征对提高行波保护新原理的动作性能至关重要。

为此，本文首先从复合模域故障等效电路出发，推导得到区内、外故障下故障处电压表达式，揭示过渡电阻对波形的影响作用；然后分析了模量行波之间的差异性，得到反映区内、外故障的模量行波差异通项；为避免区外非金属性故障的影响，利用不对称故障下行波的折反射特征，提出了模量行波差异与折反射特征相配合的单端量保护方法；最后，利用PSCAD／EMTDC 搭建柔性直流输电模型，通过大量仿真验证本文所提保护方法能够快速、可靠地识别线路区内、外故障。

1 故障处电压波形及折反射特征分析

本文以典型真双极模块化多电平换流器（modular multilevel converter，MMC）柔性直流输电系统为例，开展故障处电压波形及折反射特征的分析，其系统拓扑结构如图1 所示。直流输电线路是长度为l的双极架空线，其端口安装电感值为Lb的限流电抗器；ZMMC_R和ZMMC_I分别为整流侧、逆变侧换流站等值阻抗；M、N 分别表示线路整流、逆变侧安装的保护；CB 表示直流断路器。本文以保护M 为研究对象进行说明，则f1为直流线路故障，其为区内故障；f2为限流电抗器与换流站之间的故障，其为区外故障；Rp、Rn和Rg组合的过渡电阻阵可表示不同的故障类型。本文规定电流的参考方向为换流站指向线路，下文涉及的电气量均指故障分量。

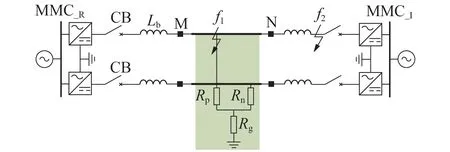
图1 真双极两端柔性直流输电系统拓扑结构Fig.1 Topology of true bipolar dual-terminal flexible DC transmission system

实际架空线路正负极存在电磁耦合，通常采用凯伦鲍尔极模变换解耦得到相互独立的线模、零模分量［17］，如式（1）所示。

式中：Fp、Fn分别为系统正、负极电气量；F0、F1分别为以正极为基准解耦后的零模、线模分量；S为凯伦鲍尔极模变换阵。

因故障暂态期间行波能量大多集中在高频段，即各换流站的等值电感占主导因素，因此忽略等值电阻与电容的影响［13］。

1.1 复合模域故障等效电路分析

现以正极接地故障为例进行分析说明。因故障类型相同，故其故障边界条件相同；但因故障位置不同，其复合模域故障等效电路中的线、零模等效网络不同，这将使故障处电压波形产生差异。对应的复合模域故障等效电路可参见附录A。

1.2 区内、外故障下故障处电压波形分析

参考附录A 得出区内、外故障下故障处电压的拉氏表达式，通过观察表达式中的参数，解析其对应的时域波形差异。

1.2.1 区内故障下故障处电压波形分析

当直流线路区内发生正极接地故障时，故障处电压可等同为初始行波，即复频域下故障处产生的线、零模初始行波可表示为：

式中：UN为线路额定电压；Rf为故障过渡电阻；Ufi，1，in、Ufi，0，in分别为发生区内故障时复频域下故障处线、零模电压初始行波；Zc1、Zc0分别为线、零模波阻抗。

若忽略线路损耗和参数频变特性的影响，则Zc1、Zc0、Rf均为常数，此时式（2）将成为阶跃波的拉氏表达式，即区内故障下初始行波为近似阶跃波。

1.2.2 区外故障下故障处电压波形分析

当直流线路区外发生正极接地故障时，故障处位于限流电抗器与换流器之间，不存在线路，因此实际上已无行波，但故障处电压可通过限流电抗器进入线路，由此在保护N处产生初始行波［18］，即复频域下故障处线、零模电压及其产生的初始行波为：

式中：L1为故障暂态期间换流器的等值电感；Uf1、Uf0分别为发生区外故障时复频域下故障处线、零模电压；Ufi，1，out、Ufi，0，out分别为发生区外故障时复频域下线、零模故障电压初始行波。

不难发现，故障处电压表达式中存在限流电抗器与线路波阻抗串联后再与换流站等值电感并联的项，其形式复杂且不满足阶跃波的拉氏表达式形式，但故障暂态期间电感占主导作用，因此可对故障处电压进行简化，可得：

式中：ℓ［·］表示拉氏变换；t为时间参数。

由式（4）易知，化简后的故障处电压可表示为初始幅值为70.7 %UN、以时间常数L2/Rf上升的指数函数的拉氏表达式。此外过渡电阻的取值将直接影响故障处电压波形，进而影响由此产生的初始行波波形。当且仅当Rf= 0，即发生区外金属性故障时，其故障处电压波形才为阶跃波；否则其为按指数形式上升的波，下文将该波称为指数上升波。

1.3 故障处折反射特征分析

对于双极系统的不对称故障而言，由于相模变换无法使故障处的电气量解耦，因而会出现模量行波之间的交叉透射现象。图2 为故障处模量行波传播简化图。图中：、分别为故障处电压、电流；为模域下的入射量；u、为模域下的反射量；、为模域下的折射量；R为Rp、Rn和Rg组合的过渡电阻阵。

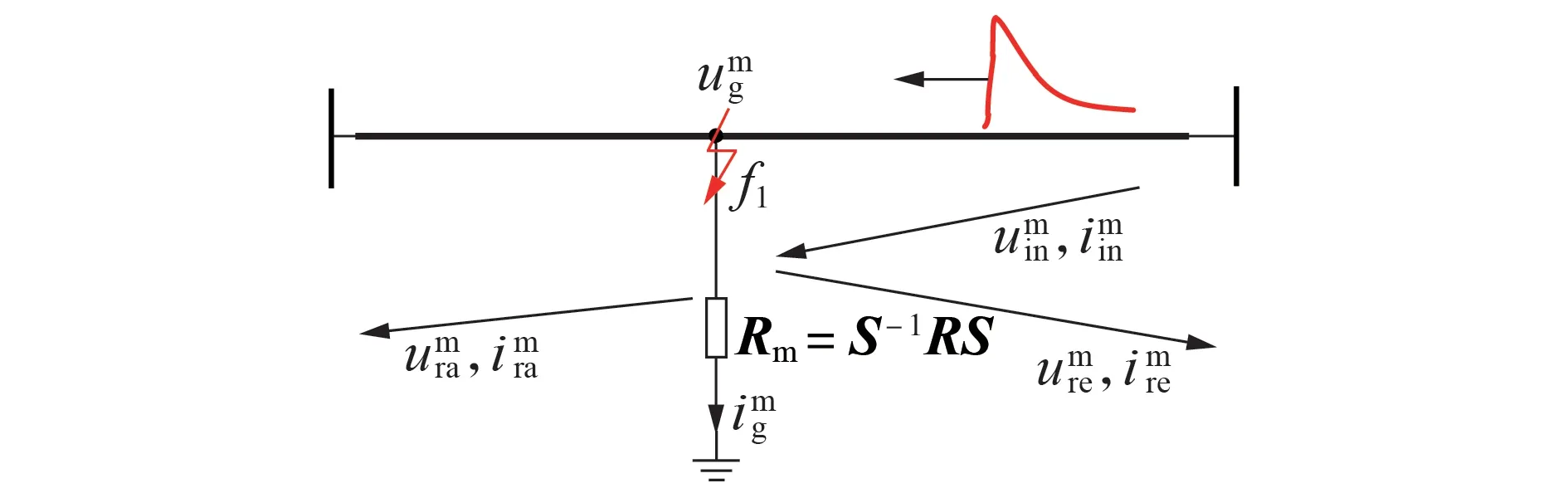
图2 故障处模量行波传播简化图Fig.2 Simplified diagram of traveling wave propagation of mode component at fault point

根据、之间的关系，结合行波传播理论可得：

式中：γ、ρ分别为故障处电压折、反射系数阵；E为阶数为2的单位阵。

现以过渡电阻为Rf的区内正极接地故障为例进行分析，相应的电压折射系数与过渡电阻阵R如式（6）所示。此时故障处折、反射系数并非对角阵，即线模与零模行波之间存在互相透射的现象。

2 模量行波差异分析

为具体揭示模量行波之间的差异性，提出可靠的故障识别判据，本文从保护M处的线、零模电流出发进行分析。

1）区内正极接地故障。

考虑到线路损耗和参数频变特性的影响，沿线传播的行波将会出现衰减与畸变现象［19］，因此复频域下保护M处的电压首行波为：

式中：U1，in、U0，in分别为发生区内故障时复频域下保护M 处的线、零模电压首行波；Ka1、Ka0分别为单位长度的线、零模的衰减系数；Td1、Td0分别为单位长度的线、零模的畸变系数；lf为故障距离，即保护M至故障处的距离。根据Peterson 法则，时域下保护M 处的线、零模电流为：

式中：Lm=Lb+L1；i1，in、i0，in分别为发生区内故障时保护M 处的线、零模电流；τ1，in、τ0，in分别为发生区内故障时线、零模电流的等效时间常数；K1，in、K0，in分别为发生区内故障时线、零模电流的等效衰减系数；v1、v0分别为线、零模行波的波速；ε（·）为阶跃函数。

观察式（9）发现，保护M 处的模量电流从0 缓慢增加至稳定值，单位时间内波形的变化量较为平缓，由此产生的后续行波也是如此，因此基于模量电流开展保护原理研究可有效避免后续行波的影响。

对于双极系统而言，零模等效网络是故障处与大地之间构成回路形成的，而线模等效网络则是两极之间构成回路形成的，因此线模波阻抗相比零模更加稳定，且满足v1＞v0、Zc0＞Zc1、Ka1＜Ka0、Td1＜Td0。然而以线模分量为例，在等效时间常数中Lm/Zc1的数量级远大于Td1lf的10 倍以上［20］，因此可忽略该部分的影响。

2）区外正极接地故障。

区外故障下还需考虑限流电抗器的影响，因此复频域下保护M处的电压首行波为：

式中：U1，out、U0，out分别为发生区外故障时复频域下保护M处的线、零模电压首行波。

此时根据Peterson 法则，得到时域下保护M 处的线、零模电流为：

式中：i1，out、i0，out分别为区外故障下保护M 处的线、零模电流；K1，out、K0，out分别为区外故障下线、零模电流的等效衰减系数；τ1，out、τ0，out分别为区外故障下线、零模电流的等效时间常数；τ1，ex、τ0，ex分别为区外故障下线、零模电流的额外时间常数。

当发生金属性故障时，故障处电压为近似阶跃波，Rf= 0，此时等效时间常数τ1，out、τ0，out均为无穷大，式（11）可进一步化简为类似式（8）的电流公式，同样存在1-e-t/τ项。以线模分量为例，区外故障下存在额外时间常数τ1，ex，相比于区内故障增加了限流电抗器影响的项Lb/Zc1，这使得区内、外故障下的等效时间常数存在明显差异。而发生非金属性故障时故障处电压为指数上升波，Rf≠ 0，则此时保护M 处的模量电流公式将不同于区外金属性故障与区内故障下的公式。

2.1 区内、外故障模量行波差异通项分析

根据以上对区内、外故障下模量电流的分析，现构造模量行波差异通项Dpu0-1，该通项可有效避免过渡电阻及不同极故障下零模分量极性不同的影响，实现差异量归一化的目的。

式中：iR，1、iR，0分别为保护M处的线、零模电流。

1）区内接地故障分析。

现将式（8）代入式（13）可得区内接地故障下的模量行波差异通项，如式（14）所示。

由式（14）可知，模量行波差异通项随着时间的变化将从-1 开始增加，最终稳定到某一数值。该稳定值与线、零模等效衰减系数相关。然而随着故障距离的增加，模量波速之间的差异增加，这将使得各模量行波到达保护安装处的时刻不同，反映到模量行波差异通项中则该项保持在-1 的时间更长，且分子和分母中指数项发生变化时刻不同，整体反映出随故障距离的增加而呈现减缓的上升趋势，最终到达稳定值。

2）区外接地故障分析。

同理将式（11）代入式（13）可得区外接地故障下的模量行波差异通项，如式（15）所示。

因区外金属故障与非金属故障下故障处电压波形存在明显差异，因此需分别对2 种故障情况展开讨论。

当发生区外金属性故障时，Rf= 0，此时等效时间常数τ1，out、τ0，out均为无穷大，式（15）可简化为式（16）。

观察式（14）、（16）发现，区外金属性故障的模量行波差异通项与区内故障相似，然而稳定值中增加了与模量波阻抗有关的项Zc1/Zc0，通常情况下Zc0＞Zc1，因此区外故障下的稳定值将小于区内故障；等效时间常数中同样增加了与波阻抗和限流电抗器有关的项Lb/Zc1、Lb/Zc0，等效时间的增加将使得模量行波差异通项上升速率进一步变慢。加之此时故障距离大于区内故障距离，因此模量行波差异通项保持 -1的时间将达到最长，且上升速率相比区内故障将变慢，最终稳定在小于区内故障的稳定值。

由上述分析可知，区内故障与区外金属性故障下模量行波差异通项的差异明显。

当发生区外非金属性故障时，Rf≠0，此时等效时间常数τ1，out、τ0，out不为无穷大，这将使式（15）中与τ1，out、τ0，out有关的指数项不恒为1，该常数随着Rf的增加而减小，但始终存在τ1，out＞τ1，ex、τ0，out＞τ0，ex。该情况会加速模量行波差异通项上升的速率，以更快的速度到达稳定值。此时较快的模量行波差异通项上升速率将不同于区外金属性故障，区外高阻故障可能与区内末端故障下的上升速率相似，因此有必要区分该情况。

2.2 利用折反射特征识别区外非金属性故障

针对区外高阻故障下模量行波差异通项的变化趋势可能与区内末端故障相似的情况，现利用保护M处的线模电压反行波进行识别。

当发生区外非金属故障时，呈指数上升形式的故障电压经限流电抗器进入线路后形成电压行波并向保护安装处传播。而发生区内末端故障时因故障处至保护M 的距离lf大于线路全长的1/2，因此保护在感受到电压首行波后，会感受到来自对侧边界反射并经故障处折射的后续行波，两同极性波出现的时间间隔为2（l-lf）/v，其中v为行波传播波速。相应地，行波传播网格图可简化为图3。

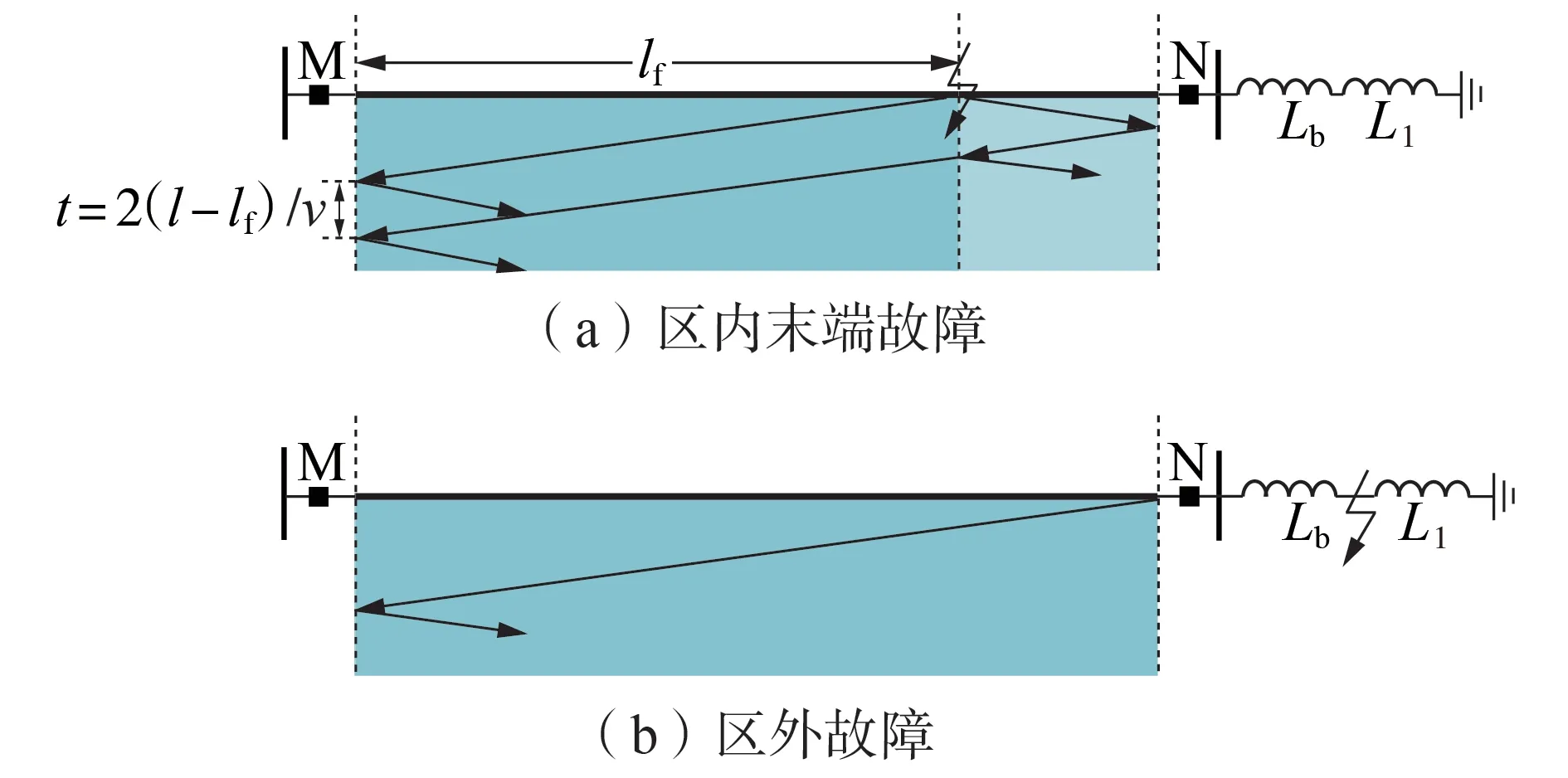
图3 区内、外故障下的行波传播网格Fig.3 Lattice of traveling wave propagation for internal and external faults

现探究该后续行波的极性与幅值，由式（6）不难发现，来自对侧边界反射的后续行波在故障处存在少量模量行波互相透射的现象，但绝大部分模量行波会折射到自身模量中。以线模分量为例，当Rf= 0时，线模折射到线模的系数为Zc0/（Zc0+Zc1）；当Rf= ∞时，折射系数为1。即故障处的折射不改变行波的极性，且幅值大于入射波幅值的1/2。因此，发生区内末端故障时，保护M 在适当的时窗下可先后辨识出2 个同极性（负极性）的线模电压反行波，而区外非金属性故障无法呈现该特性。综上所述，利用故障处折反射特征可有效识别区外非金属性故障。

3 基于模量行波差异的单端量保护方法

本文利用模量行波之间的差异识别区内、外故障。根据2.1节的分析，区内与区外金属性故障的模量行波差异通项存在较大的差异性，故采用积分放大此差异，如式（18）所示。然而区外高阻故障下，该积分值可能与某些区内末端故障下的积分值接近，因此还需利用行波在故障处的折反射特征，检测保护在启动后规定时间内线模电压反行波中同极性（负极性）波个数，从而实现区内末端故障与区外非金属性故障（区外高阻故障）的甄别。

式中：A为模量行波差异通项在时间Tn内的积分值，该值通过通项的当前值累加实现，因此无量纲；ts为保护启动时刻。为实现故障的实时检测，将模量行波差异保护与利用故障处折反射特征识别区外非金属故障的方法相结合，下文所提保护Ⅱ段中线模电压反行波检测时窗也为Tn。

3.1 故障识别判据及定值选取原则

综上所述，将模量行波差异与折反射特征相配合以构成单端量保护方法，可实现线路故障的准确识别。本文所提方法可分两段实现，即保护的故障识别判据如式（19）所示。其定值选取原则如下：选取一设定故障位置下保护M 出现2 个同极性波的时间间隔作为检测时窗和模量行波差异通项的积分时间Tn。当线路故障距离小于设定的故障距离时，模量行波差异通项的积分值满足Ⅰ段判据；故障距离大于该设定值时，积分值满足Ⅱ段判据。

式中：Afu为Ⅰ段判据的整定值，该值与上文选取的故障位置发生故障时对应的模量行波差异通项的积分值有关；Aset为Ⅱ段判据的整定值，该值与区外金属性故障下模量行波差异通项积分值有关；n( )uR，1，f为保护M在启动后Tn时间内检测到线模电压反行波中同极性（负极性）波的个数。

3.2 同极性反行波的检测方法

因B 样条小波的二进尺度小波变换模极大值（wavelet transform modulus maxima，WTMM）的位置与信号的尖锐变化点一致，且具有滤波消噪功能，因此本文利用该方法对保护安装处线模电压反行波的幅值和极性进行检测［21］。若检测时窗Tn内存在连续2 个同极性（负极性）的奇异值，则证明在首行波到达后，保护又叠加了对侧边界反射后经故障处折射的同极性波，即发生了区内末端故障；若仅检测出一个同极性（负极性）的奇异值，则证明该奇异值仅由故障初始行波造成，在检测时窗Tn内无后续行波叠加，即发生了区外故障。

3.3 保护启动与故障选极

本文所提单端量保护方法沿用文献［18］的启动判据和故障选极判据，进行保护启动和故障极的甄别，此处不再赘述。当启动判据识别出线路故障发生后，将会激活故障识别判据进行故障区段判断，最后在故障选极判据的作用下跳开故障线路。

4 仿真验证

为验证所提模量行波差异与折反射特征相配合的单端量保护方法的正确性，在PSCAD／EMTDC中搭建拓扑结构如图1 所示的±500 kV 的真双极两端柔性直流输电系统。整流侧采用定直流电压控制，逆变侧采用定有功功率控制；直流线路长度为500 km；柔性直流系统参数、架空线路的频变参数模型及杆塔模型见附录B；Lb=100 mH；保护采样频率为50 kHz。

以保护M 为例进行仿真分析，启动判据阈值Δset整定为150 kV；选极判据阈值Δpset整定为100 kV；故障识别判据中选取设定的故障距离为350 km，此时积分时间与WTMM 的检测时窗Tn均为1 ms；保护Ⅰ段和Ⅱ段的Afu、Aset分别整定为-26 p.u.、-36 p.u.，整定结果分别与设定的故障位置350 km 处接地故障、区外金属性接地故障时模量行波差异通项的积分值，以及考虑的可靠系数有关。

4.1 区外故障处电压及传播至保护处首行波

现分析区外发生不同过渡电阻的接地故障时，故障处电压波形及该电压通过限流电抗器进入线路后形成行波并经线路传播，最终到达保护M 处形成的电压首行波波形。该分析过程以线模为例进行说明，验证上文理论分析的正确性。

图4 为发生不同过渡电阻的区外正极接地故障时故障处线模电压及保护处首行波的波形。图中t=0为首行波到达保护安装处的时刻。由图可知，过渡电阻不改变故障处电压初始值，其值为353.5 kV。当Rf= 0 时，故障处电压为近似阶跃形式，此时传播至保护M 处的电压首行波畸变与衰减达到最大；当Rf≠ 0时，故障处电压为指数上升波。

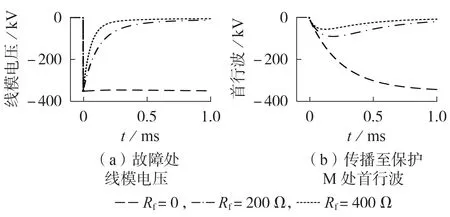
图4 发生区外故障时的故障处电压及保护处电压首行波Fig.4 Voltage at fault point and initial traveling wave when external fault occurs

4.2 模量行波差异通项分析的有效性验证

对于本文搭建的双极系统而言，当线路发生不对称故障时，存在线、零模分量，因此本节针对双极系统的单极接地故障，进行模量行波差异通项分析的有效性验证。

由于所提通项使模量行波之间的差异归一化，该项原则上不受过渡电阻的影响，即保护原理具有较强的耐受过渡电阻能力。图5 为发生区内、外正极接地故障（本节进行分析时分别简称为区内、外故障）时的模量行波差异通项曲线。图中：不同故障距离下的区内故障过渡电阻均设定为400 Ω；区外故障过渡电阻分别设定为0、400 Ω；行波到达保护安装处的时刻设置为0；模量行波差异通项为标幺值。对图5的具体分析如下。

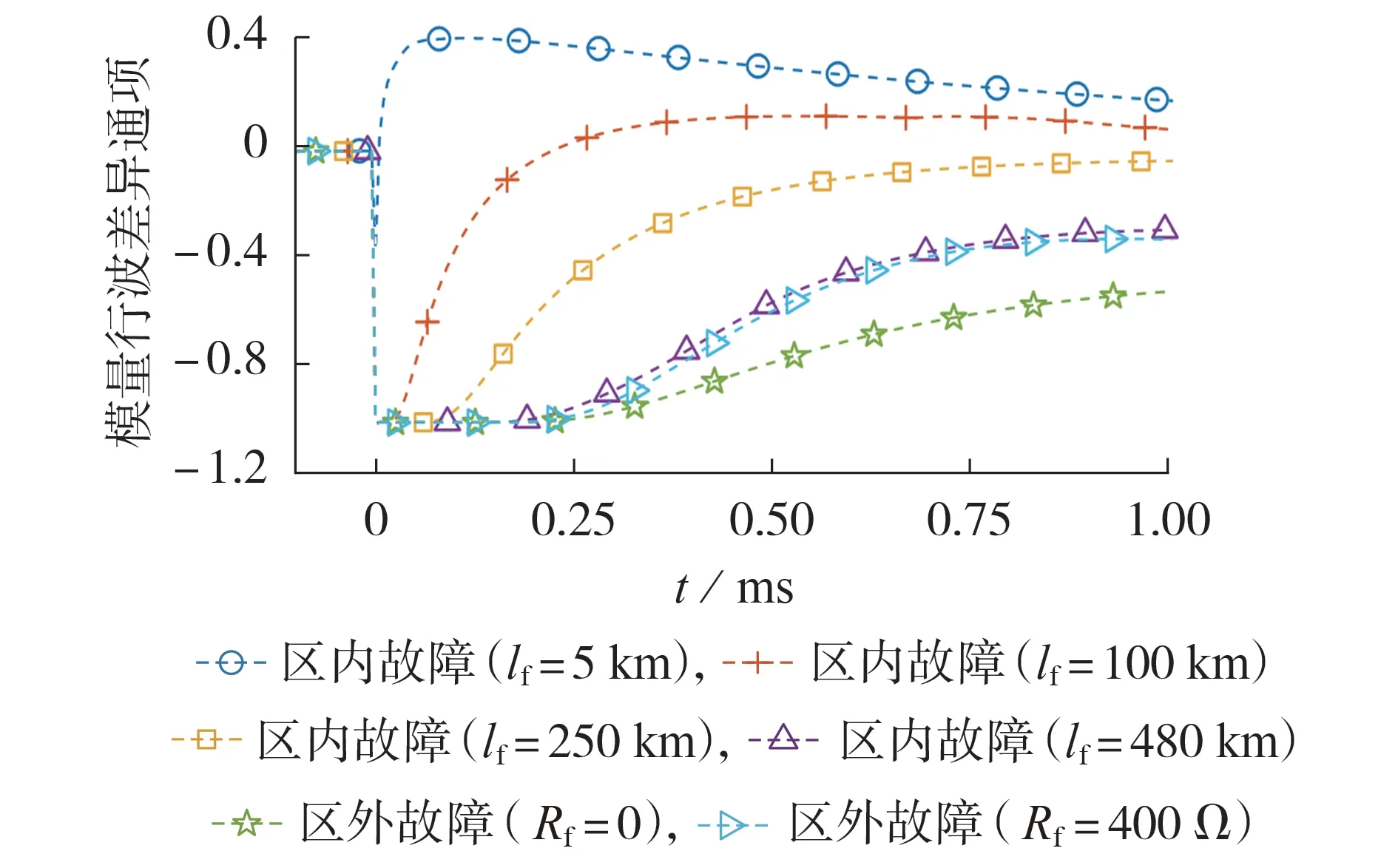
图5 区内、外故障下模量行波差异通项Fig.5 General terms of difference of mode components in case of internal and external faults

1）区内故障与区外金属性故障。

当与保护M 相距5 km 处发生区内故障时，模量行波的等效时间常数占主导因素且零模等效时间常数小于线模等效时间常数，因此对应的模量行波差异通项将从0 上升然后趋于稳定值。当故障距离增加时，线、零模行波将不再同时到达保护M且存在一定的时差，反映到通项上为曲线将保持一段时间为-1 p.u.，随后以不同上升速率达到稳定值；随着故障距离的增加，其保持 -1 p.u.的时间将增加，最终稳定值将下降。即区外金属性故障与区内故障在模量行波差异通项曲线上升速率方面有较大的差异性，如图5 所示，因此可采用式（18）所示的积分方式放大模量行波之间的差异。

2）区外非金属性故障。

过渡电阻为400 Ω 的区外故障对应的模量行波差异通项与故障距离为480 km 的区内故障对应的模量行波差异通项接近，若仅利用保护Ⅰ段判据识别故障，则可能会引起保护误动，进而危及系统安全。因此合理利用行波的折反射特征，采用WTMM检测保护启动后一段时间内线模电压反行波的负极性奇异值个数，可正确识别区内末端故障与区外非金属性故障，即保护Ⅱ段。

4.3 所提保护动作性能分析

区内、外不同故障条件下所提保护的动作情况如附录C表C1、C2所示。由表可知：在端口及近端1和10 km 处发生故障时，本文所提保护可正确识别故障；随着故障距离的增加，模量行波差异通项积分值A逐渐降低，但仍与逆变侧区外金属性故障有较为明显的差异。此外保护Ⅱ段判据在识别区内末端故障与区外非金属性故障方面有不错的效果；然而随着区内末端故障的深入，保护安装处检测到2 次同极性反行波出现的时间间隔将缩短，这将加大WTMM 检测波形奇异值的难度。为应对这一问题，本文所提保护可借助对侧保护出口的动作信号，向本端发送信号协助本端保护切除故障线路。

4.4 保护Ⅱ段判据检测结果分析

由表C1 可知，当故障距离为400、480 km 时保护判据Ⅰ段不动作、Ⅱ段动作。此时Ⅱ段判据需要借助WTMM 对保护安装处线模电压反行波的幅值和极性进行检测，以求得检测时窗Tn内的负极性波个数。现以故障距离为400 km、过渡电阻为400 Ω为例的区内末端高阻故障进行分析，WTMM 检测结果如图6所示。

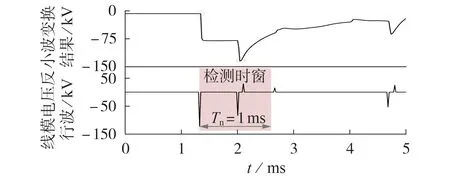
图6 区内末端高阻故障的WTMM检测结果Fig.6 WTMM detection results in case of internal high-resistance fault at end of area

由图6 可见：检测时窗从保护启动后行波数据中首个模极大值出现时刻算起，1 ms 时间内将连续检测到2 个负极性波，即满足Ⅱ段判据。区内远距离高阻故障将被可靠识别。同理，由表C2 可知，当区外发生过渡电阻为400 Ω 的故障时，Ⅱ段判据将可靠不动作，保护不存在拒动的风险。WTMM 检测结果如附录C图C1所示。

4.5 抗干扰能力分析

对表C1、C2 中的部分仿真数据附加信噪比为30 dB 的高斯白噪声，保护动作结果如附录C 表C3所示。通过多次的测试可知，本文所提保护能够在30 dB 的噪声下正确识别线路故障。因故障识别判据中存在积分计算环节，因此利用积分可有效实现对噪声的抑制。此外，由2.2节可知，对侧保护反射、经故障处折射的电压反行波幅值大于入射波的1/2，因此噪声对其影响不大，不影响保护利用WTMM 进行电压反行波的同极性奇异值检测，此外WTMM 自身具有较好的抗噪能力。由此可知，本文所提保护在一定的噪声干扰下可正确识别线路故障。

4.6 与现有保护方法对比

1）基于行波峰值时间的保护方法。

现以保护M 为例，测试文献［14］提出的基于行波峰值时间的保护方法性能，采样频率的选取、故障距离的设定、行波到达时刻的规定均与本文所提保护方法一致。不同故障条件下保护安装处的线模电压幅值如图7所示。

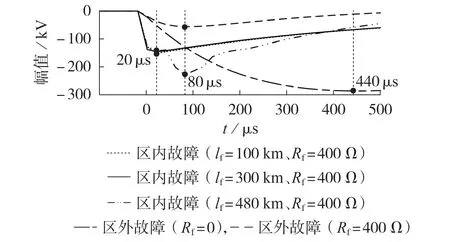
图7 不同故障条件下保护安装处的线模电压Fig.7 Line-mode voltage at relay protection under different fault conditions

由图7 可知：故障距离为100、300 km 的区内故障下线模电压的峰值时间远小于区外金属性故障情况下对应的时间，且具有良好的耐过渡电阻能力；然而随着过渡电阻的增加，区外非金属故障下线模电压的峰值时间将显著减少，极端情况下甚至可能与受后续行波影响的区内末端故障下线模电压的峰值时间相同，这使得保护的灵敏度大幅降低。而本文所提保护方法在以上故障条件下均可正常动作。

2）基于波前陡度的保护方法。

在同样的条件下测试文献［15］提出的基于波前陡度的保护方法性能，结果如图8 所示。图中电压反行波为标幺值。由图可见，区内与区外金属性故障下线模电压反行波的波前陡度存在明显差异，然而区外非金属故障下故障处电压为指数上升波，这将进一步导致保护安装处线模电压反行波的波前陡度减缓不大，可能会引起保护误动。

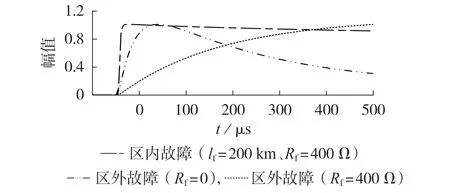
图8 最大值归一化后保护安装处的线模电压反行波Fig.8 Backward traveling wave of line-mode voltage at relay protection after maximum value normalization

3）基于SIEMEMS行波保护方法。

参考文献［12］对故障发生时刻进行考量，现取相同区内故障条件（过渡电阻、故障距离和故障类型）下，电压差分最大值在不同故障时刻的最小值进行灵敏度校验。参考本文搭建的系统拓扑，采样频率为10 kHz。以保护M 为例，验证SIEMEMS 行波保护对于线路故障的灵敏性。图9 为遍历所有故障位置的正极电压差分Δup/Δt。由图可见：在过渡电阻为200 Ω 且故障距离大于110 km 时，电压差分值将小于保护阈值，此时SIEMEMS 行波保护会拒动；同理当过渡电阻为300 Ω且故障距离超过50 km时，该保护无法正确识别区内故障。而本文所提保护方法在识别区内故障时具有较高的灵敏性，不存在SIEMEMS行波保护的问题。

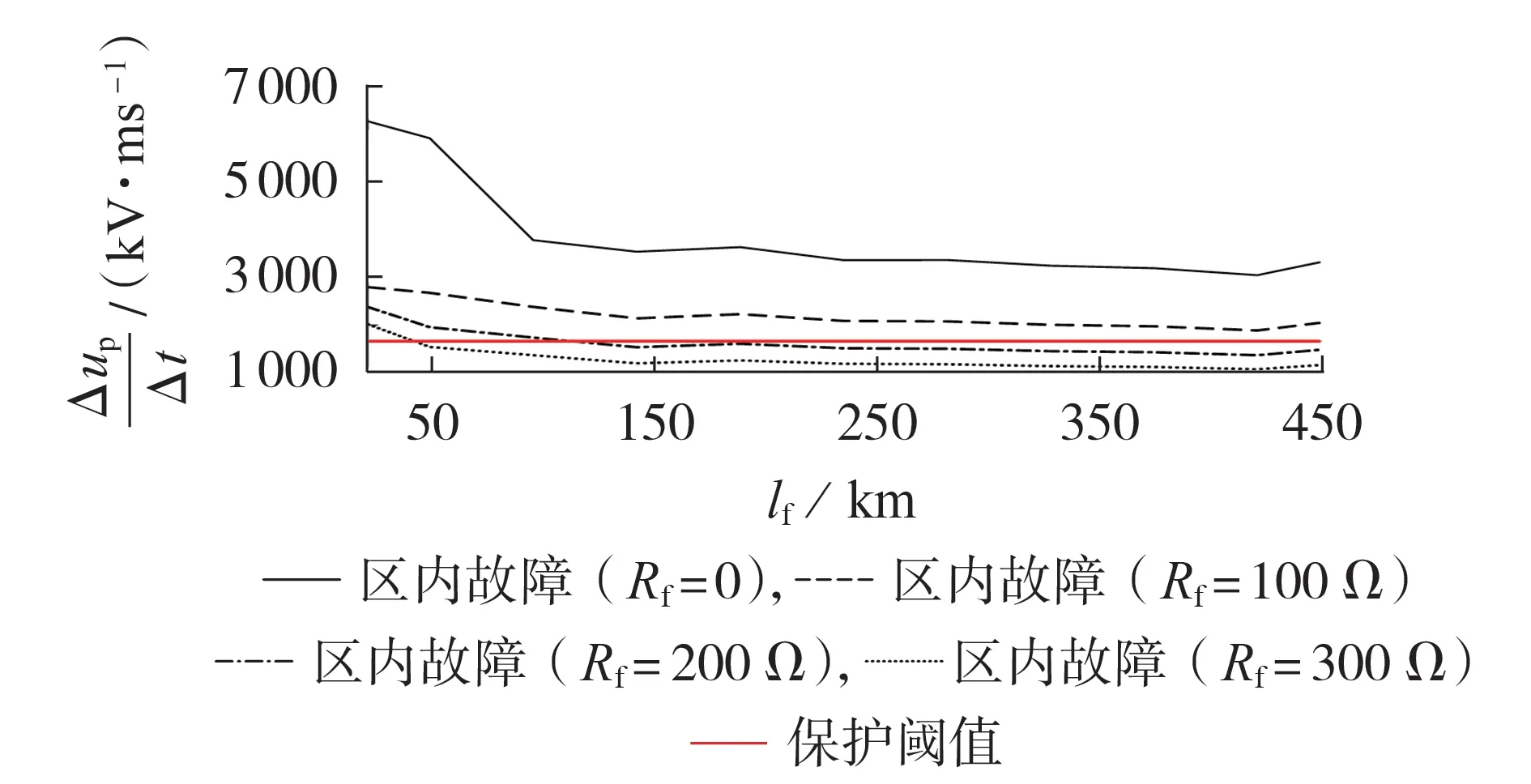
图9 区内正极接地故障的电压差分情况Fig.9 Voltage difference in case of internal positive pole-to-ground fault

5 结论

基于波形特征的行波保护在发生近端故障时易受后续行波影响，保护动作性能降低。且区外非金属性故障时故障处电压并非阶跃波，因此由故障处电压为阶跃波开展的保护原理研究并不严谨。为解决上述问题，本文从复合模域故障等效电路出发，解析了区内、外故障时故障处电压波形差异，随后分析了模量电流之间的关系与行波在故障处的折反射特征，进一步提出了模量行波差异与折反射特征相配合的单端量保护方法。理论分析和仿真验证结果表明，本文所提方法可有效避免区外非金属性故障的影响，具有较好耐受过渡电阻能力与抗干扰能力。

附录见本刊网络版（http：//www.epae.cn）。