基于扩展卡尔曼滤波的固定翼无人机姿态解算方法
2023-11-10弋英民王柯颖苑易伟薛向宏李余兴刘柏均王烨琛
弋英民,王柯颖,苑易伟,薛向宏,李余兴,刘柏均,王烨琛
1(西安理工大学 自动化与信息工程学院,西安 710048)
2(西安理工大学 陕西省工业图传与控制应用校企联合研究中心,西安 710048)
1 引 言
姿态解算通常是利用数据融合算法标记传感器有用信息,按照坐标系转换关系计算姿态信息,进而进行组合导航的.精确、稳定的姿态信息在姿态控制[1]、目标跟踪[2]和组合导航[3]等众多领域都发挥着至关重要的作用.固定翼无人机(Unmanned Aerial Vehicle,UAV)凭借飞行速度快,航程距离远,运载能力大的特点,在边境巡逻、战术侦察、灾情监视等领域也发挥着重要作用.
固定翼无人机飞控系统中的惯性测量单元(Inertial Measurement Unit,IMU)是以多轴组合的传感器单元,将传感器的输出值通过滤波算法进行数据融合,可以抑制姿态误差的累计,消除噪声干扰,从而获得正确的姿态角.目前在固定翼无人机上采用的姿态解算方法,普遍使用的有卡尔曼滤波器[4]、Mahony互补滤波器[5]和Madgwick梯度下降法[6].本文在扩展卡尔曼滤波算法的基础上,结合互补滤波器和动态梯度下降法,用于解算固定翼无人机姿态角.
卡尔曼滤波器(Kalman Filter,KF)广泛用于数据融合和状态估计,它遵循两个通用步骤:预测和更新[7].通过调节卡尔曼增益来最小化误差,使得估计值接近真实值.文献[8,9]将线性卡尔曼滤波器用于MARG(Magnetic,Angular Rate and Gravity)传感器方位估计,利用3个传感器构成两层结构的Kalman滤波器,最后和Madgwick算法进行了对比验证,根据静态和动态均方根误差值显示,Kalman滤波器表现出的性能更加准确和稳定;文献[10]在考虑到外部加速度的动态条件下设计了基于卡尔曼滤波的姿态估计算法,该算法能在短期内快速动态条件下表现出较高的精度,但一旦存在长时间的高外部加速度,该算法的优势逐渐降低;文献[11]针对MARG传感器系统的姿态估计误差问题,采用BP神经网络尝试补偿姿态误差,主要通过训练传感器数据,以补偿卡尔曼滤波估计的姿态,实验结果证明融合了神经网络的KF算法角度误差有效减小,但改善效果有限.
扩展卡尔曼滤波器(Extended Kalman Filter,EKF)是指对非线性系统进行了线性化的状态观测.其动态性能良好,仅依靠参数矩阵进行解算,不影响估计精度.文献[12]基于扩展卡尔曼滤波理论,选择陀螺仪的姿态四元数和漂移偏差构造状态方程,利用正交化方法从加速度计和磁强计的输出中获取姿态四元数作为测量向量,该EKF算法模型能够准确表示无人机在动、静态条件下的姿态;文献[13]采用双扩展卡尔曼滤波(DEKF)并行地对飞行器的数据进行预测和更新,第一个EKF负责估计俯仰和横滚角信息,第2个EKF用于估计航向信息,能够限制磁干扰对偏航估计的影响;文献[14]以姿态偏差、陀螺仪偏差以及运动加速度构造状态向量,采用误差扩展卡尔曼滤波,即乘法EKF,该方法具有一定的可行性和可靠性,但误差模型的建立依旧比较理想.以上利用EKF算法及其改进方法减小线性化误差有限,并没有解决无人机在面临高机动情况下稳定性较差的问题.
互补滤波器(Complementary Filter,CF)通常起到数据融合和的作用,它以计算量小的显著优势,成为了姿态角估计方面最广泛的滤波器之一.文献[15,16]采用互补滤波器的融合方法来求解姿态角,该方法能显著提高解算速度,降低处理器精度;文献[17,18]分别基于FPGA平台和IMU单元设计了一种改进型互补滤波算法,满足了无人机姿态解算的精确度和实时性需求;文献[19]提出了一种互补滤波器级联结构,分别采用非线性结构修正陀螺仪偏差、线性结构估计姿态角.但是互补滤波器在高频端截止频率附近衰减较慢,导致处理后的数据存在误差,精确度较低,飞控系统出现滞后现象.
梯度下降算法是四元数误差沿着负梯度方向,通过不断迭代误差函数,直到误差值小于某一阈值,从而得到该时刻的最佳估计值.卢等人在四旋翼飞行器上分别比较了梯度下降和互补滤波融合算法与自适应互补滤波算法,最终自适应互补滤波算法试验效果更佳[20];文献[21]在四元数的EKF姿态估计基础上,利用动态步长梯度下降算法对加速度数据进行补偿,对GPS测量数据的磁畸变进行消除,在快速运动情况下提高了姿态解算的精度.虽然梯度下降法一定程度上可以消除噪声干扰,但需要设计一个合适的步长,太大会导致求解的姿态角度发散,太小没有收敛效果.
本文提出一种基于扩展卡尔曼滤波的固定翼无人机姿态解算方法,在姿态角保持稳定时采用标准EKF进行解算,姿态角发生剧烈变化时采用改进EKF方法进行解算.改进方法在EKF的基础上加入互补滤波器和动态梯度下降法,分别作用于陀螺仪和加速度计两个传感器,可有效减小EKF算法线性化误差,解算结果稳定性更高.首先利用小波包分解原理对原始数据进行去噪,然后用改进互补滤波之后的陀螺仪测量数据求得初始姿态作为状态变量.用加速度计测量数据作为量测变量,用动态梯度下降法对运动加速度加以抑制,给定雅克比矩阵,经EKF方程组迭代计算得到当前时刻的姿态角四元数.该方法减少了传统方法各自使用时的局限性,提高了解算精确度和稳定性.
2 系统模型
2.1 姿态描述与欧拉角转换
机载NED坐标系(North-East-Down Coordinate System):通常以地心作为坐标的原点,N表示地球北向、E表示地球东向、D表示地球地向,故又称作是北东地坐标系,该坐标系我们用n系表示.
机体轴坐标系(Body Frame):它是无人机惯性导航的基准坐标系,其原点O取在无人机的重心位置,X轴指向机身前进方向,Z轴垂直于X轴向下而Y轴与X、Z轴构成右手系,由此指向机身右侧,故又称作是前右下坐标系,该坐标系我们用b系表示.机载NED坐标系与机体轴坐标系的组合关系如图1所示.

图1 机载NED坐标系与机体轴坐标系的组合关系Fig.1 Combination between airborne NED coordinate system and airframe axis coordinate system
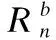
(1)
姿态角是无人机在机体轴坐标系中参考机载NED坐标系绕固定点旋转三次完成转换的,通常按照Z、Y、X轴的顺序产生欧拉角,由此可得Z轴偏航角yaw(记为ψ),Y轴俯仰角pitch(记为θ),以及X轴滚转角roll(记为φ)在三维空间中所对应的旋转矩阵分别为:
(2)
q=q0+q1i+q2j+q3k
(3)
其中,q0,q1,q2,q3是实数,i,j,k表示虚数单位.

(4)
(5)
2.2 扩展卡尔曼滤波算法
EKF姿态解算部分主要分为两个过程,预测过程和测量过程.对应公式为式(6)和式(7):
(6)
(7)

在时间预测过程中,将得到的陀螺仪三轴角速度矢量,以四元数形式通过一阶龙格库塔法进行首次估计,即:
(8)
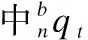
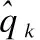
(9)
其中wk是近似为白高斯噪声的状态噪声,状态转移矩阵Φ(bw,Δt)是用零阶积分计算的:
(10)
在状态更新过程中,首先对于一个三轴加速度计,把任意时刻测得的加速度矢量,作为观测变量,记作:
z(k)=[abx(k)aby(k)abz(k)]T+vk
(11)
式中abx(k)、aby(k)、abz(k)是在载体坐标系中重力加速度分别对应x、y、z轴的方向分量,vk是近似为白高斯噪声的测量噪声.
接着,根据旋转矩阵进行坐标转换得到如式(12)所示:
(12)
则系统的观测方程可以表示为式(13)所示:
(13)
根据式(13),h(x(k),k)为非线性函数,需要通过泰勒级数展开将非线性函数在当前估计状态的平均值附近线性化,求得雅克比矩阵为:
(14)
则量测过程:
(15)
最后为了保持四元数单位范数的性质,在时间预测和状态更新阶段结束时,都要采用归一化步骤对姿态估计值进行归一化处理.
3 改进扩展卡尔曼滤波的姿态解算方法
扩展卡尔曼滤波在预测参数时要求模型具有先验性与已知性,然而在工程实践中通常难以获得准确的数学模型,且非线性系统在线性化的同时,也会带来线性化误差,因此对非线性依赖严重的模糊系统,求解参数的效果并不明显.应用互补滤波可以有效减轻温漂误差,但在进行欧拉角与四元数的转换以及PI积分时,将角度误差带入到解算的欧拉角中,导致积分出的四元数项精度不够,因此误差累积也始终影响着互补滤波算法的解算结果.梯度下降法和互补滤波算法都是通过向量叉乘并求导得到误差向量进行补偿,一般适用于低频低速运动,但如果是强机动、高速飞行的环境,就需要和其他算法进行结合以提高解算精度.
针对3种传统滤波算法各自使用时的局限性,且为了提高固定翼无人机的环境适应能力和解算过程的稳定性,本文在EKF算法的基础上,加入动态梯度算法和互补滤波算法,用于无人机惯性测量单元陀螺仪和加速度计两个传感器的数据融合与姿态解算.
3.1 陀螺仪的角速度补偿
惯导单元IMU传感器在不同频率范围内有不同的动态响应优势,由于陀螺仪与加速度计又具有频率互补性,因此可以结合陀螺仪和加速度计的性能优势,采用互补滤波算法结合不同频的输出信息,使得表征结果更加贴合实际值.主要步骤如下:
1)计算误差

(16)
设加速度计3个轴的值分别为ax,ay,az,对其分别进行求模和归一化处理,如下式所示.

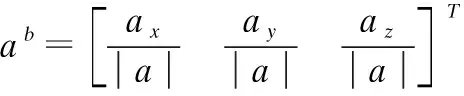
对求得的gb、ab经过矢量乘积即可得到互补滤波的角速度校正值e,如式(17)所示:
(17)
2)PI误差补偿
由于陀螺仪传感器在使用过程当中先天性具有受温度影响数据逐渐漂移的不足,因此使用PI控制器(Proportional Integral controller)进行误差补偿,可降低传感器输出数据受自身性能的影响.控制的效果取决于比例可调增益P和积分增益I这两个参数,PI控制器滤波公式如下:
(18)
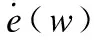
(19)
3.2 运动加速度的抑制处理
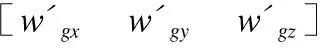
梯度下降法可以表示为:
xn+1=xn-μ×▽F(xn)
(20)
式中:x表示运算前后自变量的值,▽F(xn)表示目标函数的梯度,下标n表示搜索次数,负号表示沿着梯度的负方向逼近极点,即搜索方向,μ表示在搜索方向上的步长.
设加速度计归一化后在机体轴坐标系中为ab=[axayaz]T,当重力向量在机载NED坐标系中为gn=[0 0 1]T时,理论重力加速度与加速度计测得值相减得到的误差函数用四元数表示法为:
(21)

(22)
将式(9)简单定义为迭代公式:
(23)
则根据梯度下降法的迭代过程式(9)可演变为:
(24)
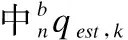
(25)
其中,α>1,w为陀螺仪的测量角速度;Ts为系统的采样时间,均为正相关.为了增强四元数估计的动态跟踪特性,设置与物理方向速率相关的自适应步长,如式所示:
(26)
另外,为了降低运动加速度对高速状态下的飞行器的干扰.定义δk为加速度计测量值的可信因子:
(27)

(28)
将以上迭代公式应用于状态向量姿态四元数的估计中,可以避免线性化误差,提高估计精度.
3.3 强机动高速运动的干扰消除办法
在无人机的高速、高空运动的作业环境下,需要面临强干扰、高运动加速度的恶劣问题,为了保证飞行的稳定性和解算的精确性,并在此基础上尽量降低处理器计算的复杂程度,本文提出一种根据阈值进行算法动态切换的解算方法.
由于EKF算法是基于前一时刻的姿态估计值进行更新迭代的,那么当飞行姿态保持稳定不变时,标准EKF足以解算出稳定姿态角;当飞行姿态发生剧烈变化时,由于EKF算法本身的递归特性,再加上微分过程带来的线性化误差问题,本文提出一种基于阈值法优化改进扩展卡尔曼滤波的固定翼无人机姿态解算方法,改进方法在EKF的基础上加入互补滤波器和动态梯度下降法,分别作用于陀螺仪和加速度计两个传感器,可有效减小EKF算法线性化误差,提高解算过程稳定性和环境适应能力.
在EKF算法解算姿态角的过程中,姿态角的更新主要是通过四元数微分方程的求解进行的,而姿态角的剧烈变化会直接体现在陀螺仪的输出角速度上,不稳定、不准确的角速度会导致求解的姿态角误差增大.因此本文以陀螺仪的输出角速度变化值为判定姿态角剧烈变化的阈值,判断式为式(29).当判定大于某一阈值a时,认为此刻姿态角发生了变化,需要使用改进EKF算法进行姿态解算,否则使用标准EKF算法进行姿态解算.
(29)
最终陀螺仪经过了预测过程,加速度计经过了测量过程,将两者输出的结果通过迭代合并得到了三轴姿态角的四元数形式,并通过欧拉角反解公式求解出三轴姿态角.公式如下:
(30)
3.4 姿态解算的整体流程
本文在EKF的基础上,加入PI补偿的互补滤波算法和动态步长的梯度下降法,整体姿态解算流程图如图2所示.算法步骤为:
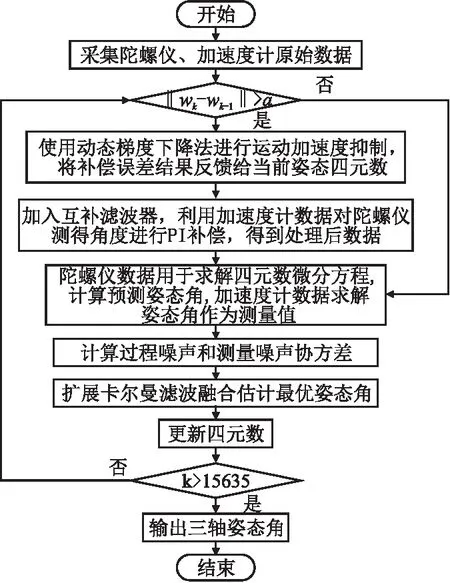
图2 姿态解算整体流程Fig.2 Flowchart of posture solution
1)采集IMU惯导单元陀螺仪、加速度计传感器原始数据,并对原始数据进行小波包降噪;
2)如果判定角速度w1变化值小于阈值a,那么将陀螺仪输出值计算的姿态四元数作为初始状态向量,将加速度计输出加速度作为量测向量,使用标准EKF算法实现估计角度和测量角度的融合,计算出姿态四元数和协方差矩阵;
3)如果判定角速度w1变化值大于阈值a,那么使用动态步长的梯度下降法求解加速度计输出的误差函数,并补偿给姿态四元数,使用PI补偿的互补滤波算法求解陀螺仪输出角速度的误差向量,并以补偿后的姿态四元数和输出加速度作为状态向量和量测向量,使用EKF算法解算得到最优估计角度;
4)把得到的最优估计角度作为下一次迭代的初始角度,并不断利用四元数微分方程进行姿态角的更新,最终得到一组稳定的最优估计四元数角度;
5)通过反解欧拉角公式最终得到一组最优估计欧拉角度.
4 测试过程及结果分析
本文主要采集传感器ADIS16488A三轴陀螺仪和加速度计的数据,数据集共计六组,静态测试每组13558个,动态测试每组15636个,频率为100Hz,即采样时间为10ms,每采集一次就进行一次数据融合和解算.解算算法中使用到的参数如表1所示.
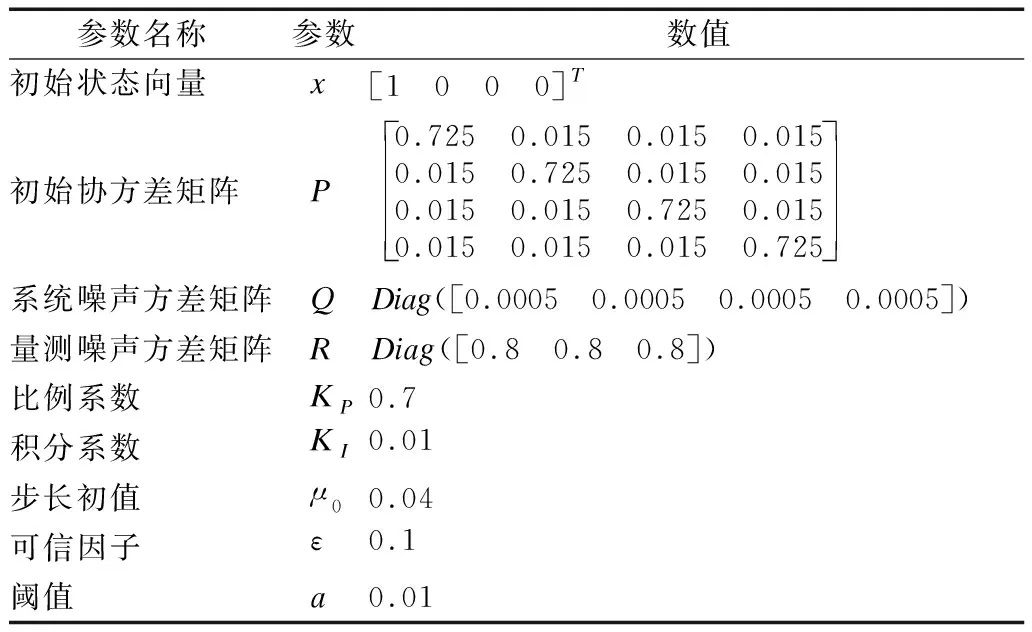
表1 实验参数Table 1 Experiment parameter
为了验证本文采用的阈值法优化改进扩展卡尔曼滤波算法的稳定性和准确性,在进行测试的同时,对标准的Mahony滤波器、EKF算法以及文献[18]和文献[21]中提出的EKF和Mahony滤波器融合算法(Mahony_EKF)、EKF和动态梯度下降法相结合的算法(DGDA_EKF)进行了算法验证,同本文中提出的改进EKF算法进行了性能比较.
4.1 静态测试
在无人机处于静置状态时,使用5种姿态解算算法对三轴姿态角进行了估计,如图3所示.每幅图中从上往下依次是Mahony滤波器、标准EKF、Mahony_EKF算法、DGDA_EKF算法以及本文提出的改进EKF算法的解算结果,参考值均为0°附近.图3(a)X轴解算的横滚角在-0.01°波动,图3(b)Y轴解算的俯仰角在-0.1°波动,图3(c)Z轴解算的航向角在-1°~1°范围波动.

图3 静态测试三轴姿态解算结果图Fig.3 Results of triaxial attitude calculation in static test
与标准EKF算法相比,单独使用Mahony滤波器,三轴解算角度均有一定的漂移误差,航向角达到最大误差2°.而在EKF 的基础上所进行的融合算法中,本文提出的改进EKF算法解算横滚角误差能保持在0.005°左右,航向角在其他解算算法均解算漂移的情况下误差保持在0.6°左右.
图4给出了静态测试下5种解算方法的后验均方根误差对比结果,实验结果证明,在5种不同的姿态解算方法中,单独使用Mahony滤波器和EKF算法静态误差较大,在EKF算法的基础上,加入互补滤波器和梯度下降法的融合算法中,本文提出的基于阈值法改进EKF解算算法后验均方根误差最小,准确度最高.
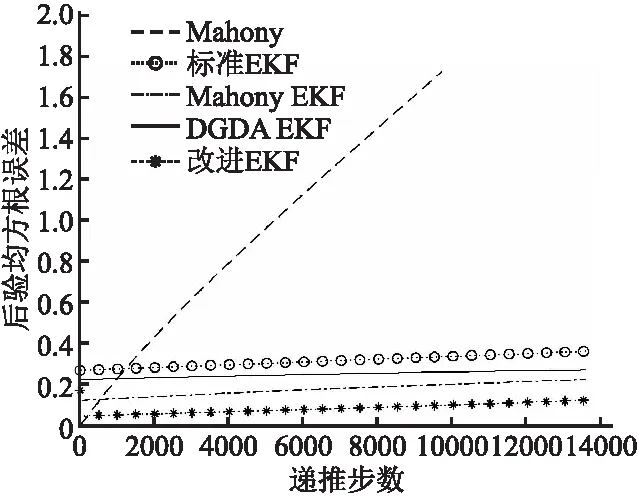
图4 静态测试解算方法误差对比图Fig.4 Error comparison results of the solution methods in static test
4.2 动态测试
动态实验是在室外对固定翼无人机进行了长达10min的试飞实验,飞行过程解算姿态角结果如图5(a)、图5(b)、图5(c)所示.无人机一开始保持稳定在0°,并分别对俯仰角、横滚角和航向角进行了单独测试,验证了姿态变化的有效性.在大约过了5min,迭代265次之后,无人机在横滚角的变化上较为明显,此时横滚角和航向角大约为20°,俯仰角依旧在0°振荡.无人机在变换完姿态后,保持姿态角度飞行了一段时间,在迭代次数达到400之后,恢复为原始角度并最终完成了此次飞行.
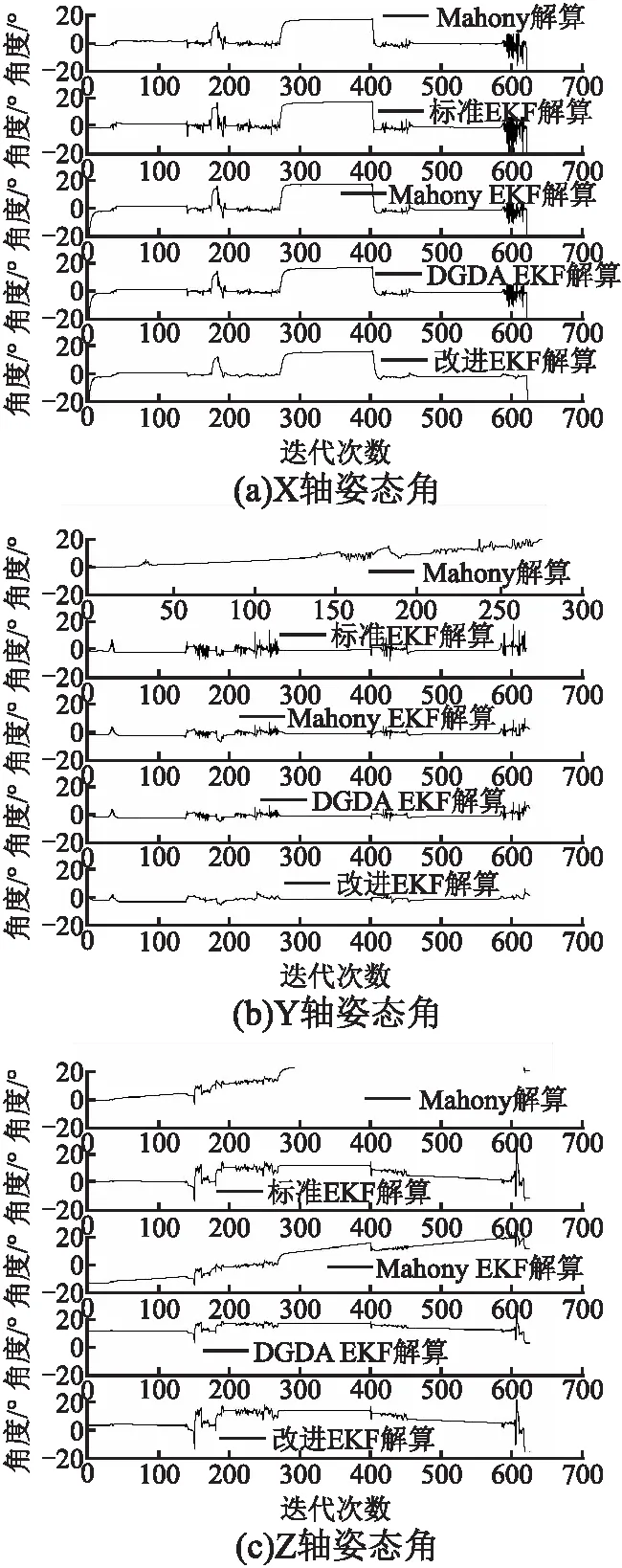
图5 动态测试三轴姿态解算结果图Fig.5 Results of triaxial attitude calculation in dynamic test
图5(a)和图5(b)分别表示惯导单元X轴和Y轴解算的姿态角结果,从图中的解算结果来看,本文提出的改进EKF算法解算过程“毛刺”较少,更加平滑,特别是在无人机最后飞行阶段,其他4种解算方法均出现了角度振荡,而改进EKF算法能够保持在较为平稳的状态,说明本文提出的改进EKF算法能够有效降低惯导单元传感器的噪声影响和环境干扰,提高解算过程的稳定性.图5(c)是Z轴解算的航向角结果,在其他4种算法解算角度一定程度上有所漂移的同时,本文提出的改进EKF算法解算稳定,能够抑制角度漂移,表现优越.
相较于单独使用Mahony滤波器,仅使用EKF算法,三轴姿态角不仅没有逐渐漂移,而且能较好的反映真实姿态角,但震荡较多,特别是在角度有一定变化或即将变化的时间点,稳定性不强,说明解算过程受环境因素、传感器自身噪声等影响很大.在EKF 的基础上分别结合了Mahony滤波器和动态梯度下降法之后,稳定性有所增强,有效改善了单一算法解算姿态角稳定性差的问题.而本文提出以扩展卡尔曼滤波器为核心解算固定翼无人机姿态角,在此基础上加入了PI补偿的互补滤波算法和动态梯度下降法,根据阈值动态选择解算算法,三轴姿态角不仅可以较好的反映真实姿态角,而且输出姿态角更加平滑,说明解算过程受噪声影响较小、算法的滤波效果更好.
5种算法解算姿态角过程得到的后验均方根误差图表如图6和表2所示.由图表中的数据可以得到,在同一组测试数据的解算过程中,改进EKF算法得到的姿态角均方误差在0.01~0.05之间,明显小于其他方法解算的姿态角均方误差,并且姿态变化范围小、稳定性高.
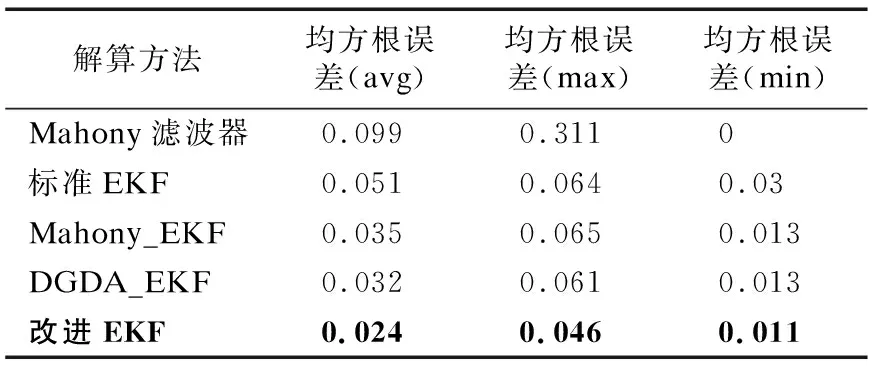
表2 解算方法误差对比表Table 2 Error comparison table of solution methods
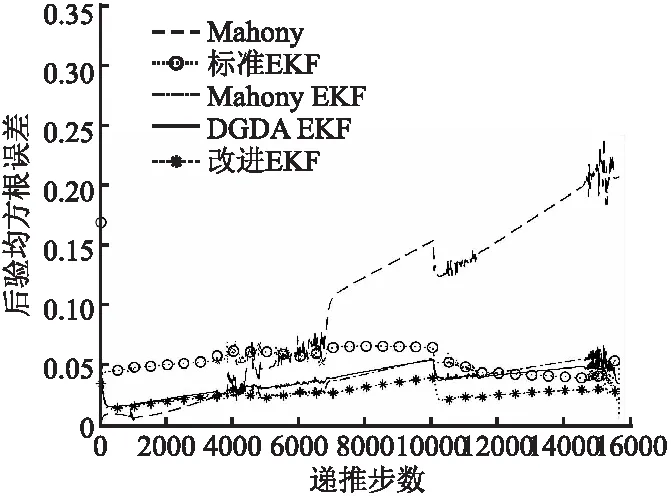
图6 动态测试解算方法误差对比图Fig.6 Error comparison results of the solution methods in dynamic test
5 结束语
针对目前常见的姿态解算算法中存在的传感器误差累积和无关变量干扰问题,本文在扩展卡尔曼滤波算法的基础上,引入PI补偿的互补滤波算法和动态梯度下降法,在飞行姿态发生变化时使用融合后的改进EKF算法进行姿态解算,飞行姿态保持稳定不变时使用标准EKF算法进行解算.依据飞行姿态变化动态切换解算方法,减少3种方法各自使用时的局限性,同时也减少传感器噪声带来的解算干扰.通过实验证明,该算法静态测试均方根误差小于0.1,动态测试均方根误差保持在0.05以内,能有效降低姿态解算的误差,提高了解算的准确性和稳定性,增强了解算系统的环境适应力.
