基于强化学习的多无人机WRSN充电路径规划方案

王 杨,单天乐,李迎春,赵传信,陈 鹏,邹荣誉

1(安徽师范大学 计算机与信息学院,安徽 芜湖 241002)

2(安徽建筑大学 智能建筑与建筑节能安徽省重点实验室,合肥 230022)

3(东南大学 计算机科学与工程学院,南京 211189)

1 引 言

无线传感器网络通常是由一组无线传感器节点构造而成,传感器节点会定期地从环境中收集信息,并通过数据汇聚等一些协议将数据传送给基站.传统无线传感网的节点内仅含一个能量有限的电池,为其工作提供能量,工作一定时间后节点的电量会用尽.小规模的无线传感器网络还能定期为节点更换电池来延长整个网络的寿命.但随着网络规模的扩大,为网络中的所有节点定期地更换电池变得越来越困难,有限的单个传感器电池能量最终会导致整个网络寿命的有限问题.为了解决无线传感网中的能量问题,国内外研究员进行了大量研究,其中最主要的方法有3种,分别是节点自我节能方式、自然能量获取方式和无线充电方式.

节能方式主要通过对数据包压缩传输、对网络进行聚类与选择动态簇头来降低传感器节点单位时间内的能耗.自然能量采集方式需要使用传感器上的能量转换器,通过该模块从自然环境中收集能量(如太阳能、风能等)以延长其寿命.但从自然环境中收集能源会带来能量来源的不稳定性(如昼夜影响、风力强弱),能量转换效率不高.无线充电方式是给网络配备无线充电源(如充电站、充电车等).充电车沿着预先设定的路径,在行驶的过程中WRSN中的各个节点进行充电.如今,利用无线充电为传感器节点或物联网设备充电的方法已广泛应用于WRSN[1].

现有的无线充电技术主要基于3大原理:1) 电磁感应技术[2],生活中很多设备都利用这一技术实现无线充电,例如手机、电动汽车等,它具有技术成熟且简单、一对一式充电[3-5]、效率较低等特点;2) 磁耦合谐振技术[6],相比电磁感应充电技术,它支持更大的空间范围内的能量传输,具有可以一对多式充电[7,8]、距离较短(10米左右)等特点;3) 无线电波技术[9],它的充电范围更广(几十公里),其具有技术要求较高、安全性不够高等特点.本文采用的是磁耦合谐振技术对网络进行充电,可以满足中小范围无线充电的要求.

对无线充电而言,小规模的无线可充电传感网只需要单小车或单无人机为网络充电,而在大规模的无线可充电传感网中,因环境复杂、面积广阔且单辆供电工具能量有限等原因,单小车或单无人机无法满足供电需求,必须要多无人机协作才可以完成充电任务.但是多余的无人机势必会造成资源的浪费,这就要求在尽可能减少无人机个数的同时优化多无人机的充电路径.文献[10]研究了将户外山地场景中无人机群的路线设计问题建模成一个多旅行商问题,并提出了一种基于部分搜索方法的多无人机飞行路径改进算法,并且提出一个山火现场巡逻的具体例子,其采用了配有摄像头的无人机.这个例子虽然没有地对空的通信链路,但是对于大型无人机群的飞行路径规划研究有一定的贡献.文献[11]研究了怎样规划好多架无人机的运动路径,以便尽早完成群体感知相关的任务.此文提出的基于双向全变邻域的搜索算法对于TSP问题的研究也具有非常重要的参考价值.

而文献[12]又将无人机飞行轨迹问题的纬度提升至三维,文献[13]所做工作的目的是将全部待充电传感器节点的总接收能量最大化,以此来研究无线能量传输WRSN网络中的无人机飞行路径规划方案.

现有研究中,全局路径规划的方法比较常用,如图搜索法、RTT算法和人工势场法等[14].但是由于全局路径规划方法都需要建立完整的模型,如果是复杂的环境计算开销则会很大;现实情况下,无人机在复杂多变的环境中掌握全局信息十分困难,想要采用确定性的方案来实现最优路径规划是不太可能的.由于近期人工智能[15]的发展,出现了许多基于人工智能的路径规划方法,其中比较典型的方法有神经网络方法、模糊逻辑方法[16]等,这些方法具有一定程度的智能性,在面对不同的场景时,不论环境是否动态变化都有着出色的性能表现,并且具有很强的泛化能力.

由于机器学习技术的快速发展,人们尝试使用深度学习(Deep Learning,DL)与强化学习(Reinforcement Learning,RL)方法来对路径规划等相关问题进行解决[17].其中最为典型的是采用马尔科夫决策模型的Q-Learning算法[18],它是一种监督式的学习方法,可以通过学习并根据环境的变化为无人机规划出一条更好的无碰撞路径.许多现有的RL方法只关注单个无人机场景.文献[19]中提出,在单个无人机基站服务的相关场景中使用RL与基于Q值表的Q学习相比更具优势,它不以长时间训练为代价,且不对环境做出任何假设.在文献[20]中,作者只研究了基于表的无人机数据收集的Q学习,解决了特定类别物联网中的数据采集.文献[21]中研究了为地面用户服务的多无人机路径规划,采用基于表的Q学习算法,基于相对复杂的3步算法,包括使用遗传算法对用户进行分组,然后在两个独立的实例中进行部署和设计Q学习算法,证明了所研究的优化问题为NP-hard,认为Q学习是解决此类问题的有力工具.

针对现有研究没有很好地解决多无人机飞行中存在的多约束和时空协同等带来的问题,提出了基于强化学习的多无人机协同无线可充电传感网充电路径规划方案(MC-CPP,Multi-UAV Collaborative Charging Path Planning),把多无人机充电路径规划问题的网络模型映射到深度强化学习MDP中,解决了WRSN中多无人机充电路径的设计问题.本方案首先利用Voronoi法将WRSN中的传感器节点划分至若干个充电单元中,由此可选择合适的充电位置从而有助于无人机对其进行一对多或一对一式充电;然后设计奖励函数机制,将问题转化为奖励最大化问题并采用改进的Q-learning对无人机进行路径规划;最后采取改进方法(如神经网络法、贪婪策略法等)使得路径分配更为智能和高效.最终得到一个多无人机无线可充电传感网充电的路径规划方案,仿真结果表明了该充电方案的有效性与优越性.

2 系统模型

2.1 网络系统模型

本网络模型为一部署在三维空间内的多无人机辅助的无线可充电系统模型,u个无人机U={U1,U2,…,Uu}被安排向网络中n个物联网设备节点N={N1,N2,…,Nn}提供充电服务,网络中物联网设备节点Ni的坐标是(Xi,Yi),无人机群从基站S=N0(设置在网络中心处)出发后以一定的飞行高度H和飞行速度v沿着规划路径给网络中的各待充电节点充能,最终返回基站.路径规划系统模型如图1所示.

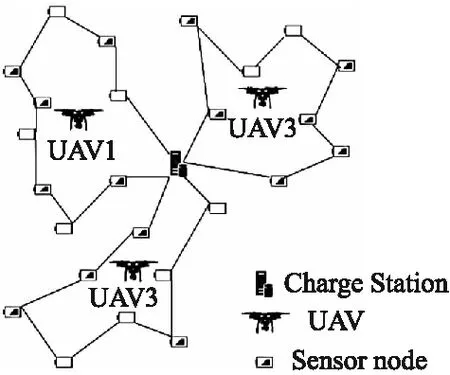
图1 多无人机路径规划系统模型Fig.1 Multi UAV path planning system model

2.2 能量消耗模型

无人机的飞行功率与悬停功率[22]可分别表示为Pmov=Pprove,Phov=Ppro(vt=0)=P0+Pi,其中P0和Pi是常数,P0代表UAV叶片轮廓功率,Pi代表UAV悬停时的感应功率;Ppro是无人机的推进功率;ve是飞行状态下的平均转子感应速度;vt为无人机飞行速度.

2.3 无线能量传输模型

节点Si的能量接受功率Prec可以表示为:Prec=ηPtrahi,jt,这里0≤η≤1表示无线射频能量传输的效率.无线充电中能量接收和充电时间关系如图2所示.

图2 接收能量和充电时间关系Fig.2 Relationship between received energy and charging time

2.4 碰撞避免策略

多无人机存在判断碰撞及碰撞避免的问题:很多情况下,计算得到的路径会有交点.路径相交并不代表无人机会产生碰撞,只有当无人机同时到达一个交点时才会碰撞.当两架无人机一起向同一交点飞行时,如果它们之间的距离小于ds,那么两者的安全圆就会相交.满足:

mini,k=1,…,n,j≠k[dik(j)]≥ds,j=1,2…m-1

(1)

时,多无人机可以避免碰撞,其中ds为安全距离,dik(j)为第j个等分点时,第i个UAV与第k个UAV之间的距离,表示为:

(2)

2.5 多无人机协同路径规划

Step 1.用Voronoi图法进行环境建模,选取合适的出发点,并综合考虑路径长度、节点能量等因素对网络使用深度强化学习奖惩函数法求解最优路径;

Step 2.采用神经网络方法对结果优化,为每架无人机规划出一条满足时空协同约束条件的可飞行路径;

Step 3.判断每个无人机飞行路径是否能够满足安全性约束条件,避免与其他无人机发生碰撞;

Step 4.如果所得路径满足不了要求,可以令任务时间短的无人机停止等待另一架通过后通行或者改变可能冲突的无人机对节点的充电顺序.

多无人机充电路径规划流程图如图3所示.

图3 充电流程图Fig.3 Charging flow chart

其中Voronoi图法用于选取充电停止点,其具体方法如图4所示.

图4 Fig.4

Case 1.如图4(a)所示:3个及多个节点的Voronoi交点处,当节点在UAV最大可充电范围内;

Case 2.如图4(b)所示:两个节点的垂直平分线上距离两节点最近的点,当节点在UAV最大可充电范围内;

Case 3.如图4(c)所示:当其它节点都不在UAV最大可充电范围内,这时要单独给此节点充电.

3 状态奖励函数

在无线可充电传感网中,UAV在自身能量满足充电需求的情况下既要给分配的节点进行充电,又要尽快完成全部充电任务并且返回基地.所以本文所设计的状态奖励函数为两个部分构成,一个是充电项,另一个是目标引导项,充电项负责提示UAV为每个节点充电,目标引导项的目的是使UAV能够选择快捷的路径到达目的地.

3.1 充电项设计

本文依据标准正态分布建模充电项,用Ep表示节点消耗能量.Ep越小说明需求越小,会得到更大的惩罚奖励值.充电项采用函数f(Ep)来表示,如公式(3)所示:

(3)

另外,由于一个充电周期内同一节点只需完成一次充电,可以设置已完成充电的节点惩罚函数值无穷大.

3.2 碰撞避免项设计

当多无人机发生碰撞时,将获得负奖励.当两个安全圆相互碰撞时,称之为伪碰撞.类似地,当UAV与每个其他单位重叠,称之为真正的碰撞.训练中,可以通过惩罚伪碰撞来减少实际碰撞的次数.碰撞避免项用函数f(Cp)表示,如公式(4)所示:

(4)

3.3 目标引导项设计

为了让UAV既能给目标节点充电又能快速靠近目标地T,用Dus1表示UAV与下一待充电节点的距离(km),用Dus2表示UAV与下下个待充电节点的距离,目标引导项如公式(5)所示:

(5)

α叫做间隔,是一个超参数,它的值取决于所处环境与实验的要求.经数次实验得到一个合适的α值为0.0475.

将充电项、碰撞避免项和目标引导项结合起来,得到一个状态奖励函数,其符合本文模型,如公式(6)所示:

Rstate(Dus1,Dus2)=fcharge(Ep)+fcollision(Cp)+
ftriplet(Dus1,Dus2)

(6)

4 Q-Learning算法

Q-Learning算法是一动态规划的强化学习算法,Q是指在某一时刻的某一状态下智能体(agent)采取某一动作所期望能够得到的奖励或惩罚.环境会根据agent的动作反馈相应的回报,因此Q-Learning算法的核心就是搜索并综合所有可能的状态与选择的动作构建出一张Q值表,然后根据Q值来选取可以获得最大收益的动作.Q-Learning算法同时为马尔科夫决策过程MDP(Markov Decision Process)的另一种表达,其整体框架如图5所示.

图5 Q-Learning算法框图Fig.5 Q-learning algorithm block diagram

本方案的第一步是把UAV充电路径规划问题用数组{S、A、R、P}建模为MDP,数组中的S是UAV的所处状态空间,A为其动作空间,R为奖励回报值(由状态奖励函数给出),P代表状态转移的概率.例如,系统在时间t选择了动作at并飞至下一待充电节点,环境信息由状态st转移至st+1,环境状态st以如下概率转移至st+1:

P[s=st+1|st,at]=P[st,at,st+1]

(7)

策略的集合由π表示,π(a|s)表示在某一状态s所采取下一步可能发生的动作a的概率.

π(a|s)=P(At=a|st=s)

(8)

在策略π的作用下,累计奖赏值函数为:

Vπ(st)=Rst(a)+γ∑st+1P[st,at,st+1]Vπ(st+1)

(9)

式(9)中,Rst(a)表示当前状态下采取行动a可以立即获得的奖励回报,Y∈[0,1]为衰减系数,代表着下一步的回报对于当前状态回报的影响系数.本算法的目的是找出状态空间中最优的解π*,可以让每一st状态的值都可以达到最优,如公式(10)所示:

π*=argmaxVπ(s),(∀s)

(10)

式(10)是指所得最优解π*可以令值函数Vπ(s)取到其可能取得的最大值.

设计动作值的Q函数如下:

(11)

其中,Q*(s,a)为在状态s时采取动作a后所得的最佳奖励值之和.目前的状态s和目前动作a,在这之后会采取策略π,状态s将以概率P(s,a,st)变化至下一可能状态st+1,可以得到Q算法的基本形式如公式(12)所示:

Q*(s,a)=R(s,a)+γ∑P(s,a,st)maxQ*(st,at)

(12)

根据式(12)可得:

π*=argmaxQ*(s,a),(∀s)

(13)

Learning的算法大致流程如下:UAV在状态s时首先在所有可能采取的动作中选择a动作,然后根据执行了动作a到达下一节点后所获立即奖励以及接受了当前状态动作值的估计来评价动作a的好坏与对总奖赏值的影响程度.通过重复所有状态下的所有动作,UAV便可通过判断长期折扣回报来学习总体上的最佳行为,即节点充电顺序及路径规划.Q函数的值会不断迭代最终收敛至最优,表示为:

Q(s,a)←Q(s,a)+α[r+γmaxQπ(s′,a′)-Q(s,a)]

(14)

其中α为学习率;Q(s,a)表示在状态s处采取动作a时获得的总估值函数,r代表“眼前利益”,即当前状态s下采取动作a后到达下一节点可以得到的收益.

在满足了一定条件的情况下,随机给定的状态s以及动作a,在第k次(k趋近∞)时更新迭代的值函数终将收敛于函数Q(s,a).

通过多次强化学习的训练,系统能够得到在确定的充电地点下应该选择哪一节点作为下一待充电地点,从而获得节点充电顺序并由此构成UAV最优的充电轨迹,UAV采用这条路径对节点充电可以将获得的累计奖励最大化.基于状态奖励函数的无人机路径规划方法如表1所示.

表1 基于状态奖励函数的无人机路径规划方法Table 1 UAV path planning method based on state reward function

5 基于改进Q学习的路径规划

5.1 Q值近似

多无人机采用Q-Learning算法来训练并更新策略,标准的Q学习算法通常利用Q值表存储不同状态时选择不同动作分别反馈的Q值,但是由于状态空间与动作空间的不断扩大会致使储存Q值所占内存空间指数形增加.为避免此问题出现,一般采取神经网络来近似地预测不同状态组合下的Q值,从而把Q值表更新与保存转化为函数的拟合问题,从而解决因储存Q值表所造成的内存开销问题.

本文采用如图6所示的“输入层-隐藏层-输出层”三层结构的神经网络,并且设置隐藏层的神经元个数为2×n,其中n为无人机数量,此时可以让算法达到不错的效果并且消耗相对低.这里的隐藏层是线性整流单元(ReLU),输出层的激活函数是一个线性函数通过3层神经网络来拟合Q值,如公式(15)所示:

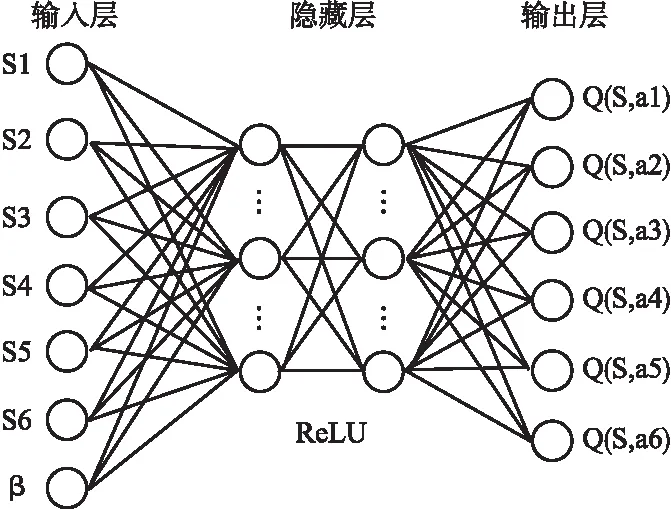
图6 神经网络结构图Fig.6 Neural network structure diagram

Q(s,a)=θ1S1+θ2S2+…+θnSn+β

(15)

其中θ={θ1,θ2,…,θn}表示神经网络中的参数,β表示偏置,Si表示第i台无人机的状态.本文的研究中,采用随机梯度下降的方法来训练神经网络.公式(16)表示为:

L(θ)=E[(TargetQ-Q(s,a,θ))2]

(16)

其中r表示在s状态下执行a动作所获得奖励,TargetQ=r+γmaxQ(s′,a′,θ)是期望的Q值,Q(s,a,θ)是实际的Q值,通过两者之间的误差值可建立此损失函数,目的是使当前的Q值逼近期望Q值.

5.2 贪婪策略(ε-greedy)

在衡量继续开发和探索扩展二者之间权重时,ε-greedy是常用的策略之一.这种贪婪策略在智能体做决策时,会用一较小正数ε(<1)的概率来任意选取动作空间的一个动作,剩下1-ε的概率选取已有动作中回报最大的动作,这样可以避免策略收敛于局部最优.本文采取此贪婪策略:为了得到最优的学习策略,在任务刚开始时将探索的概率ε设置为0.5,随着任务调度次数的增加逐步缩小ε,最终保持在0.06,这样算法初期可以尝试更多的策略,而后期减少探索偏向于使用优化过的策略.

5.3 算法实现

多无人机协同充电路径规划(MC-CPP)如表2所示,MC-CPP算法的输入为新的任务S(这里指待充电节点),输出为At(最佳动作).算法的基本流程为:当一个新的待充电节点进入系统,系统首先获取无人机状态信息,然后初始化经验回放池,再使用ε-greedy策略来确定无人机下一步动作的选择.即根据当前的无人机状态计算并保持所有下一步动作的Q值,再以ε的概率抽取无人机动作空间中的一随机动作,以1-ε的概率采取可以使当前Q值最大的动作,然后将动作分配给多无人机执行,最后更新系统状态、保存信息至经验回放池中并更新神经网络中的参数θ值.

表2 MC-CPP算法Table 2 MC-CPP algorithm

6 仿真结果与分析

6.1 实验环境

本章设计了一个模拟程序来模拟数据传输过程中传感器节点的能耗相关参数.模拟器通过修改传感器节点的初始能量、能量消耗速率等,可以模拟出本文中的WRSN场景.UAV的速度设置为6m/s,无线充电功率为30W,飞行成本为50J/m.负惩罚奖励ε是-10,奖励折扣Y等于0.9,在神经网络的设计中,使用的是具有两个隐藏层的全连接前馈神经网络.第1层和第2层各拥有256个神经元.本节通过仿真实验来验证本文算法的性能,将环境建模为1000×1000区域并采用Voronoi图的方法对区域进行划分.

在强化学习过程中,一个学习周期是多个学习步骤的序列,一个学习周期在如下3个事件中任意一个发生时结束:case1:完成充电任务并到达基站位置;case2:UAV发生碰撞;case3:已达到预先规定的最大学习步骤数.

如图7所示,4架无人机为区域内100个传感器节点进行充电的路线示意图,采用Voronoi法所以只需遍历图中47个停止点即可,利用强化学习及神经网络可获得多无人机飞行路径.其显示了传感器节点为100、基站个数为1时充电停止点分布情况以及充电路径.可将100个传感器节点全部覆盖,且都满足充电策略.

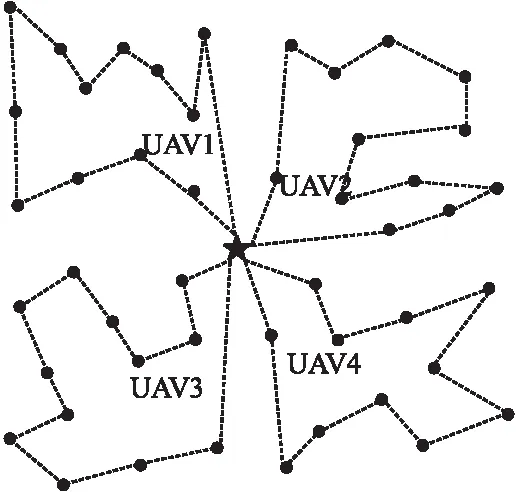
图7 无人机飞行路径Fig.7 UAV flight path

6.2 实验参数设置

Q-Learning算法中的学习过程及无人机设备的参数符号、含义与相关设置如表3所示.

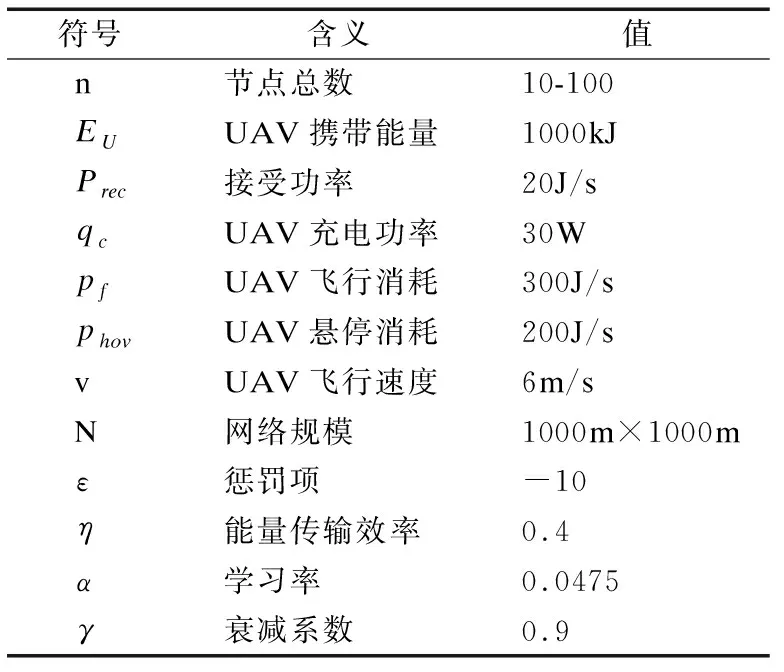
表3 参数表Table 3 Parameter table

本文场景下的WRSN中有n辆UAV在充电中心处出发,按照顺序沿着各自路径对路径上待充电的节点补充能量,完成任务后返回基站补充无人机自身电能,这就是一轮次的充电调度.根据本文充电策略,UAV估计每次移动的回报值,随着不断地进行训练与迭代,UAV的总飞行距离也随之不断下降,直到Q值收敛于极大值,便得到此环境下满足要求的最佳飞行路径.表4、表5为此环境下衰减系数Y和惩罚项ε对奖励值、死亡节点、飞行距离的影响.

表4 γ的影响Table 4 Influence of γ

表5 ε的影响Table 5 Influence of ε

其中飞行距离的单位为km.

由此可以得到,收集到的充电奖励随着γ值的增加而增加,而当γ=0.9时,没有传感器节点耗尽能量.而引入惩罚值的目的是尽量减少网络中死亡节点的数量,当ε=0时,死亡节点数为5,随着ε的增加,死亡节点的数量逐渐减少,当ε=-10时,死亡节点数为0.

图8为同一实验环境下无人机数量与充电覆盖率之间的关系,可以得到改进的Q-Learning算法比传统Q学习算法的充电覆盖率平均高出12.4%,改进算法在无人机个数为4时对WRSN的充电覆盖率高达97%,已满足最小充电覆盖率约束.然而同等数量无人机情况下,传统算法充电覆盖率为78%不能满足90%充电覆盖率要求,如需达到要求则至少需5架无人机,此时会增加无人机个数导致资源浪费.

图8 无人机数量与充电覆盖率关系Fig.8 Relationship between the number of UAVs and charging coverage

对比算法的充电覆盖率最高可以提升至92%,而MC-CPP的充电覆盖率能够提升至100%,而且对比算法所消耗的能量一直大于MC-CPP算法,这是由于MC-CPP算法具有更优的全局计算能力及智慧高效的特点,不仅满足了节点覆盖率与无人机飞行消耗的要求,还将无人机自身能量消耗降到最低,而对比算法则因智能性欠缺而无法达到这种效果.从图中可以看出MC-CPP在无人机数量刚好满足需求时,算法的表现差异较大,由此可得MC-CPP算法在提高节点覆盖率和减少无人机数量方面更为优越.

图9是由实验模拟所得的多无人机产生碰撞的概率,从中可以看出随着迭代次数的增加,多无人机碰撞概率从一开始的0.9%左右降低至0.4%左右.其中两个无人机时产生碰撞的概率最小并保持在0.25%～0.81%之间,4个无人机时产生碰撞的概率最大并保持在0.39%～0.9%之间.由此可得,本方案的多无人机碰撞概率很低,可以满足安全性约束条件.

图9 多无人机碰撞概率Fig.9 Collision probability of multiple UAVs

训练损失值和时间的迭代关系图如图10所示,展示了训练损失函数的收敛速度,由此图可得到损失函数的值在前1000次迭代内迅速下降,在迭代2000次时基本稳定下来.这是由于起初的动作对奖励值的影响程度很大,损失函数值的下降会很迅猛,之后随着迭代次数的增多,训练损失值会慢慢靠近最优值,从而可得到合适的网络参数值.

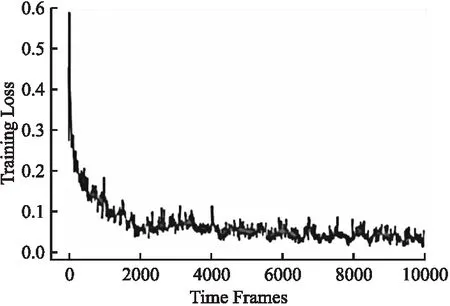
图10 迭代关系图Fig.10 Iterative graph

6.3 对比实验

本文算法与其他4种算法进行对比实验,分别为:

时空充电调度算法(TSCA):是一种按需充电算法,考虑时空信息的按需调度算法.其主要目标是最小化死亡节点的数量,次要目标是最小化UAV的移动距离,主要方案是由传感器节点发送的这些充电请求首先根据它们的充电截止时间进行排序,然后用最大努力重新排列.

最近工作优先算法(NJNP):允许UAV选择空间上最近的传感器节点作为下一个传感器来充电.

贪心充电算法(GC):一种使评估函数方程值最大化的移动设备充电算法.

随机算法(RA):它随机选择下一个传感器节点为充电节点,UAV在每次完成充电任务后都会到达.

图11展示了4种对比算法与本文提出的MC-CPP算法获得奖励值和迭代时间的关系.由图可知:1)随着时间变化,所有算法的累积奖励值都持续增大;2)起初计算量较小时,4种对比算法和MC-CPP算法奖励值相差不大,之后MC-CPP在25个训练周期处累计奖励值迅速增加,这是由于在任务刚开始执行时,距离较远处的传感器节点并没有被覆盖,有着提升奖励值的空间;3)整体上,MC-CPP的奖励值最高,TSCA其次,再者是NJNP和GC贪心算法,奖励值最小的是RA随机算法.本文提出的MC-CPP算法最先达到峰值,之后趋于一个稳定值.

图11 奖励值对比Fig.11 Reward value comparison

UAV的能耗主要包括两部分,即给节点传输的能量和自身飞行悬停所消耗的能量.通过最小化移动距离,可以使能源利用效率最大化.如图12所示,为传感器节点个数和路径长度的关系图,展现了5种算法在路径规划及能量利用率方面的优劣性.

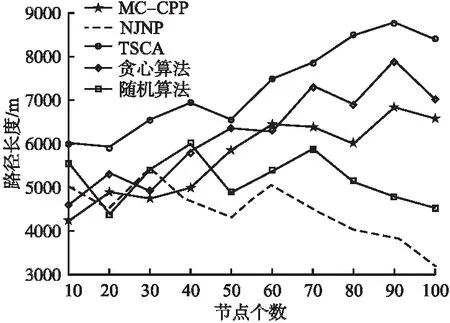
图12 路径长度对比Fig.12 Path length comparison

从整体上看,TSCA算法的路径长度最长,MC-CPP算法较短,NJNP算法得到的路径长度最短,这是由于TSCA算法为按需充电,只要节点有充电需求就会按照顺序执行充电任务所以会使得路径长度剧增,而NJNP算法会选择空间上最近的节点进行充电,所以当无人机能量耗尽时其得到的充电路径长度最短.当网络规模逐渐增大时,NJNP算法会由于节点越来越密集,路径长度变得越来越短;随机算法由于采取随机选择节点进行充电,其得到的路径长度较不规律;其余3种算法得到的充电路径长度都随着节点数量的增加而逐渐增加.其中TSCA算法得到的平均充电路径长度为7276m,贪心算法所得长度为6225m,MC-CPP得到的平均充电路径长度为5691m.由此可得,本文的MC-CPP算法在平均充电路径长度方面与TSCA算法和贪心算法相比分别缩短了21.7%、8.5%.

图13为5种算法下产生死亡节点个数的对比.从整体上,可以直观的看出随机算法的死亡节点最多,其次是NJNP算法,贪心算法和TSCA的死亡节点相对较少,由MC-CPP算法所产生的死亡节点最少,且MC-CPP在节点总数超过30之前,没有传感器耗尽电池.MC-CPP确保UAV能够及时地为所有需要充电的传感器充电,而TSCA和随机算法则不能保证UAV将达到同样的结果.然而,当网络中的节点数量超过50个时,即使是MC-CPP也不能再避免节点死亡,奖励一般会下降.原因是随着网络中待充电节点越来越多,无人机个数也需要随之增加,然而,无人机的增加需要满足一定要求,在其节点覆盖率可以达到95%以上时为了减少资源浪费不会增加无人机个数,此时会产生少数传感器节点不能被覆盖而导致节点饿死的情况发生.

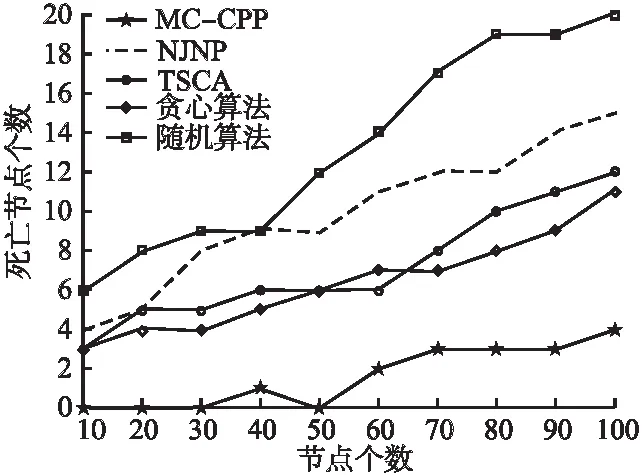
图13 死亡节点数对比Fig.13 Comparison of dead nodes

综合以上的实验结果可得,本文所提出的MC-CPP算法在大规模无线可充电传感网以及待充电节点数量变化的场景中都具有优秀的鲁棒性,其因环境动态变化而变化的可能性很小,能够根据所处环境,尽可能得到最大奖励值从而快速自适应地做出最优的充电决策,在满足充电覆盖率的同时使得无人机总飞行路径最短、能量损耗值与死亡节点数最小.

7 结束语

本文提出了一种采用强化学习方法的多无人机无线可充电传感网充电路径规划方案.本方案利用改进的Q-Learning算法,通过结合神经网络、贪婪策略、经验回放等来进行算法优化,由此可得最佳无人机数量并能够迅速准确地规划出最佳飞行路径,规划出的路径一定程度上降低了无人机在飞行路径上的能量损耗.与基于传统Q学习的方案相比,收敛速度更快,表现出了更好的路径规划性能.与TSCA等算法相比,基于奖励机制的改进Q学习算法在收敛性、奖励值和节点饿死率上优势明显.在未来的研究工作中,将对节点数量或地理位置变化情况以及环境因素(例如障碍物)等进行考虑,从而得到一种更为通用的充电规划方案.