基于改进双向峰-谷搜索算法的煤矸模型电磁波正演模拟

2023-11-10史翔予司垒王忠宾魏东顾进恒

工矿自动化 2023年10期

史翔予，司垒，王忠宾，魏东，顾进恒

（中国矿业大学机电工程学院，江苏徐州 221116）

0 引言

2022年，全国煤炭产量约45.6亿t，同比增长10.5%，创历史新高，煤炭消费量占全国能源消费总量的56.2%，这体现了煤炭在我国能源结构中的主体地位。厚煤层储量和产量在总量中的占比均为44%左右，因此厚煤层的高效开采对于我国煤炭开采行业具有重要意义。综放开采技术是我国厚煤层开采的主要方法。我国综采技术起步早，发展快，目前机采已经可以实现自动化控制，但是由于放煤过程中煤矸含量识别技术尚未成熟，放煤部分仍只能采用人工操作，极易造成欠放、过放等情况，大大降低煤炭采出率[1-2]。因此，实现放顶煤过程煤矸含量自动识别是综采自动化的重要目标。

王家臣等[3-4]利用图像识别技术将混矸率划分为投影面积混矸率、表面体积混矸率、内部体积混矸率，实现投影面积混矸率向表面体积混矸率的过渡，但井下环境低照度、高粉尘仍是制约图像识别技术实际应用的重要因素。窦希杰等[5-6]采用经验模态分解方法将综放工作面煤和矸石冲击液压支架尾梁产生的振动信号分解成多个本征模态函数分量，采用多种机器学习方法训练识别模型，其中随机森林模型准确率最高。马瑞等[7]、宋庆军等[8]依据煤和矸石与刮板输送机发生碰撞产生的声波频率的差异进行煤矸识别，但由于工作面存在大量噪声，影响结果准确性。李瑞等[9]、丁震等[10]利用红外光谱技术结合黑白校正、SG卷积平滑等预处理方法建立了煤矸分类模型，对不同矿区的煤与矸石都有良好的适用性，但是实时性较差，无法满足工程需要。张宁波等[11]、王增才[12]根据γ射线穿透煤矸混合物时发生的衰减规律，建立了煤矸混合体灰分与含矸量间的量化关系，但是不同的岩石包含放射性含量也不同，影响识别精度。

电磁波波速快，穿透性强，可以避免受到粉尘及光纤干扰的影响；电磁波携带的信息丰富，在不同电性参数的介质中所体现的传播特性也不同。放顶煤过程产生的煤矸混合物是由煤、矸石和空气形成的三相介质，各相介质的电性参数不同、空间位置分布随机且混合形式复杂。在不同组分的混合三相介质中，电磁波的传播特性也不尽相同。煤和矸石的相对介电常数差异明显，通过研究不同含矸率煤矸混合物的电性参数，可为放顶煤工作面含矸率自动识别提供新的思路和方法。为了探究不同含矸率煤矸混合物的电性差异，本文提出了一种基于分治策略的双向峰-谷搜索算法，建立了煤矸多相离散随机介质模型，基于麦克斯韦方程组及其本构关系方程，利用时域有限差分法对所建立的模型进行电磁波正演模拟。

1 煤矸多相离散随机介质模型

综放开采形成的煤矸混合物随机性较强，传统的均匀介质模型无法精准描述煤-矸石-空气的三相随机分布状态，无法为电磁波探测相关研究提供满足需求的样本。因此，需要建立能够准确描述煤矸混合物空间分布和电性参数的介质模型，在此基础上对其进行电磁波正演仿真，实现电性参数差异分析。

1.1 随机介质理论

基于随机介质理论的随机介质模型最早出现于地质学与大地构造物理学的相关研究中。地质体的相组成非常复杂，为非均介质，其中包含大量孔隙、断岩、物质夹杂等。从相结构来分析，地质体的相结构与放顶煤形成的煤-矸石-空气多相结构较为相似。随机介质可以分解为大、小2种尺度的非均匀性部分：大尺度非均性用于描述介质的背景特征，如层状连续介质模型；小尺度非均性则用于描述背景特征上的随机扰动，通常用一个均值为零的二阶平稳随机过程来表示[13]。

对于煤矸混合物随机介质模型，其相对介电常数为

式中：εm(x,y)为随机介质的大尺度非均匀性部分，与坐标(x,y)有一定关系；δm(x,y)为随机介质的小尺度非均匀性部分。

δm(x,y)在二阶平稳假设下可分解为

式中：δp(x,y)为相对介电常数变化的标准差；f(x,y)为均值为零、标准差为1的二维随机序列，其空间分布服从二维空间自相关函数。

为了灵活准确地描述实际介质，二维空间自相关l函数通常采用高斯-指数混合型椭圆自相关函数[14]：

式中：i，j分别为随机介质的自相关长度和均匀性；r为粗糙度因子。

1.2 基于分治策略的双向峰-谷搜索算法

随机介质模型是一种连续的空间分布状态，且相对介电常数随机变化[15]，然而综放开采形成的煤矸混合物是由相对介电常数存在绝对差异的煤炭、矸石、空气构成，各组成之间存在明显的相界面且满足一定体积比，因此，必须采用合适的方法进行离散性处理。

Lin Li等[16]首先提出将双向峰-谷搜索算法用于建立铝硅聚苯酯（AlSi-PHB）封严涂层的多相离散随机介质模型。其将随机介质理论与统计学方法引入封严涂层建模研究，用大尺度非均匀性描述涂层的平均特性，在该平均值上添加随机扰动，实现小尺度非均匀性描述，然后采用双向峰-谷搜索算法对随机介质模型进行离散性处理，处理后的模型在空间上离散分布且各组分满足一定体积比，能准确描述封严涂层微观形貌。综放形成的煤矸混合物与AlSi-PHB封严涂层存在多相、非均质、组成形貌随机、各组分物理性质差异大等共同特点。AlSi与PHB存在绝对密度差异，而煤和矸石存在相对介电常数的差异，因此，本文利用双向峰-谷搜索算法建立煤-矸石-空气三相介质的多相离散随机介质模型。

相对介电常数的差异源于物质的化学组成。空气的相对介电常数一般认为是1。煤的主要成分是有机物，储存电荷的能力相对较弱，属于弱极性物质，不同类型的煤的化合物成分有细微差别，其相对介电常数介于3和3.8之间。矸石的主要成分是无机化合物，储存电荷能力强，属于极性物质，根据相关文献[17-18]，取矸石相对介电常数为7。

用双向峰-谷搜索算法建立具有指定含矸率、含煤率的多相离散随机介质模型的步骤如下：

1）确定矸石、煤及空气的相对介电常数ε1—ε3。

2）根据介质中相对介电常数的分布，沿最大值方向搜索到根据含矸率设置的阈值后，将此部分设置为矸石相；同时沿最小值方向搜索到根据空气含量设置的阈值后，将此部分设置为空气相。

3）遍历网格中所有点，判断其属性值是否为矸石的相对介电常数ε1或空气的相对介电常数ε3，若是则不处理，若不是则将该点相对介电常数设置为煤炭的相对介电常数ε2。

以含矸率30%、空气含量10%、含煤率60%为例，建立多相离散随机介质模型，如图1所示，深蓝色部分是空气，浅蓝色部分是煤炭，黄色部分是矸石。

图1 算法改进前多相离散随机介质模型Fig. 1 Multiphase discrete random medium model before algorithm improvement

由图1可知，煤、矸石、空气三相之间存在明显的相界面。然而，各组分在模型区域内呈现聚集分布，局部区域呈现大量空隙或大量煤炭聚集的现象，导致部分局部无法表征整体的电性参数。例如，从纵向网格线150处入射的电磁波，其横向穿透区域大部分是相对介电常数较低的空气；而从纵向网格线100处入射的电磁波，其横向穿透区域的煤炭体积分数超过80%，从而引起电磁波正演仿真的失真。针对该问题，本文引入分治策略对双向峰-谷搜索算法进行改进。

分治策略应用递归的思想，首先将问题划分为子问题，然后对子问题递归求解，最后将子问题的解合并成原问题的解。双向峰-谷搜索算法在设定阈值后直接对整个模型空间进行建模，而基于分治策略改进的算法步骤如下：

1）将整个模型等幅划分为100个子网格并编号。

2）通过以下方法求解子网格顺序：计算子网格中的含煤率p1和含矸率φ1，并确定归一化系数（p，φ分别为设定的含煤率和含矸率），将其代入傅里叶归一化方程中进行迭代。

3）每次迭代后依据更新后的归一化系数反推出p1和φ1，并将其作为模型阈值重建子网格中的煤矸模型，直至归一化系数迭代到1，此时该网格内的煤矸含量与设定值相同，子网格求解完成。

4）将各个子网格的解按顺序合并，完成整个模型空间的建模。

改进双向峰-谷搜索算法流程如图2所示，其中虚线部分表示算法执行多次迭代。

图2 改进双向峰-谷搜索算法流程Fig. 2 Flow of improved bidirectional peak-valley search algorithm

傅里叶归一化方程可通过迭代令参数平滑收敛于1，通过更改自设定常数来调节收敛速度，其一般形式为

式中：Γ*为迭代更新后的归一化系数；a0—a4，w，b1—b4为自设定常数；Γ为原归一化系数。

同样，以含矸率30%、含煤率60%为例，用改进后的算法建立煤矸多相离散随机介质模型，如图3所示。

图3 算法改进后煤矸多相离散随机介质模型Fig. 3 Multiphase discrete random medium model after algorithm improvement

为了比较算法改进前后的性能，本文运用二值法，根据所建立模型各相的灰度值不同，将算法改进前后模型的三相单独分离出来，然后利用ImageJ软件基于面积分数进行分析。算法改进前后模型各相分布如图4所示。

图4 算法改进前后模型各相分布Fig. 4 Each phase distribution of model before and after algorithm improvement

分析结果如下：改进前模型空气相占10.28%，煤相占59.72%，矸石相占30.00%；改进后模型空气相占10.16%，煤相占59.84%，矸石相占30.00%。考虑到基于灰度值差异的二值分离法易在空气相与煤相交叉处产生混杂，从而存在一定误差，但二者误差皆在允许范围内，因此算法改进前后模型均满足设定体积比。然而从图4可看出，相较于算法改进前模型，算法改进后模型中的煤、矸石、空气三相之间不仅存在明显的相界面，且各相离散程度更大，不存在聚集现象，因此局部介质也能体现整体的电性参数，能够满足电磁波正演的介质模型需求。

2 电磁波正演模拟基础理论

2.1 电磁波基础理论

在宏观尺度上，电磁波的产生与传播都可以通过麦克斯韦方程描述，因此电磁波正演模拟的一切电磁过程都可以从麦克斯韦方程及其本构关系方程出发进行分析。麦克斯韦方程组描述了变化的磁场与电场的感应关系及变化的电流与磁场的感应关系，其微分形式为[19]

式中：∇为哈密顿算子；H为磁场强度，A/m；J为电流密度，A/m2；D为电位移，C/m2；t为时间，s；E为电场强度，V/m；B为磁感应强度，T；ρ为电荷密度，C/m³。

本构关系方程描述了电磁场中介质的电磁参数对电磁场的影响，其形式为

式中：ε为介质的相对介电常数，F/m；µ为介质的磁导率，H/m；σ为介质的电导率，S/m。

2.2 时域有限差分法

时域有限差分法最早于1996年被提出，用来计算电磁波传导问题。时域有限差分法是基于麦克斯韦方程的时域微分算法，其依据Yee网格（图5）中各场量（电场Ex，Ey，Ez，磁场Hx，Hy，Hz）分布，将麦克斯韦方程从微分形式转换为差分形式，然后以该网格单元将仿真区间离散划分，在微小网格单元上采用步进法在时间上迭代计算连续电磁场。在计算过程中通过电场与磁场相互更新，从而实现电磁波的迭代计算。

图5 时域有限差分法Yee网格Fig. 5 Yee grid of finite difference time domain method

在实际应用时，时域有限差分法空间及时间步长的设定会引起数值色散，从而使波形产生畸变和各向异性失真。然而由于计算机内存空间不能取无限小，所以数值色散不可避免。为了减小数值色散的影响，一般采取经验公式进行空间和步长选取[20]：

式中：∆x,∆y,∆z分别为空间坐标x，y，z的变化量；λmin为计算频段内电磁波在仿真空间各介质中的最小波长。

当迭代公式和空间步长确定后，时间步长可以由库朗（Courant）条件确定。库朗条件要求波在网格中的传播速度小于迭代所允许的最大速度，因此时间步长∆t的限制条件为[21]

式中c为自由空间中的光速，m/s。

3 电磁波正演模拟

为了探究放顶煤形成的煤矸混合物含矸率对电磁波传播的影响，最经济且直观的方法是建立不同含矸率的煤矸模型进行电磁波正演模拟，此方法的重点在于所建立的模型能够准确描述不同含矸率煤矸混合物的电性参数。最传统的均匀介质模型只适用于建立理想状态下的介质模型，如层状连续介质模型；使用未改进的双向峰-谷搜索算法建立的多相离散随机介质模型虽然能够描述煤矸混合物中各相随机分布的空间状态，但是电性参数呈现局部突变性，导致电磁波正演仿真结果出现随机性，无法展现真实规律；而基于分治策略对双向峰-谷搜索算法进行改进后，多相离散随机介质模型不仅能正确描述煤矸混合物各相随机分布的空间状态，还能准确刻画其电性参数，使用此模型进行电磁波正演仿真能够展现电磁波在不同含矸率煤矸混合物中传播的真实规律。

3.1 模拟环境

电磁波正演模拟如图6所示。激励平面发出一定频率的电磁波信号，接收平面接收电磁波的透射波信号，模拟区域网格空间为600×600，网格步长为0.4。由于仿真空间有限，电磁波会在仿真空间内发生多次反射，产生的反射波会扰乱接收界面的数据接收，导致仿真结果失真。为了使仿真条件更加贴合实际工况，模拟电磁波在远大于仿真区间的区域内进行传播，本文在仿真区间的边界处设置完美匹配层（Perfectly Matched Layer，PML）边界条件，用来吸收边界处的反射电磁波。

图6 电磁波正演模拟Fig. 6 Electromagnetic wave forward simulation

在电磁波探测领域，激励源常用雷克子波（Ricker），其具有延续时间短、收敛迅速、波形简单等优点。激励源的激励频率一般取12 GHz以下，激励频率过高会导致电磁波从导体的外围通过，产生“趋肤效应”。为确定正演模拟的激励频率，本文以图3所示30%含矸率的多相离散随机介质模型作为试验介质，分别将电磁波激励频率设置为2，4，6，8，10，12 GHz，从接收平面获取的信号时域图像如图7所示。

图7 不同激励频率下接收平面获取的信号时域图像Fig. 7 Time domain images of signals obtained from the receiving plane under different excitation frequencies

从图7可看出：① 不同激励频率对信号透射时间影响不大，都在3.2 ns左右，这是因为煤矸混合物介质是非色散介质，其相对介电常数与电磁波频率无关，而介质对电磁波的折射率由相对介电常数决定，根据电磁波在介质中的传播速度计算公式，无论激励频率大小，电磁波在相同组分含量的煤矸混合物介质中的传播速度均相同。② 不同激励频率的信号幅值不同，其中激励频率为2 GHz时，信号波形出现了扰动，原因是激励频率过低时信号不稳定，且低激励频率在实际工况中抗干扰性差。综上所述，采用频率为6～12 GHz的激励信号可以在保证信号稳定的前提下，信号幅值处在易于观测的区间，且避免产生“趋肤效应”。

3.2 模拟结果

用改进算法建立6种不同含矸率（0，10%，20%，30%，40%，50%）的煤矸多相离散随机介质模型，如图8所示，将其作为样本模型，以频率8 GHz的雷克子波作为激励源，开展电磁波正演模拟。

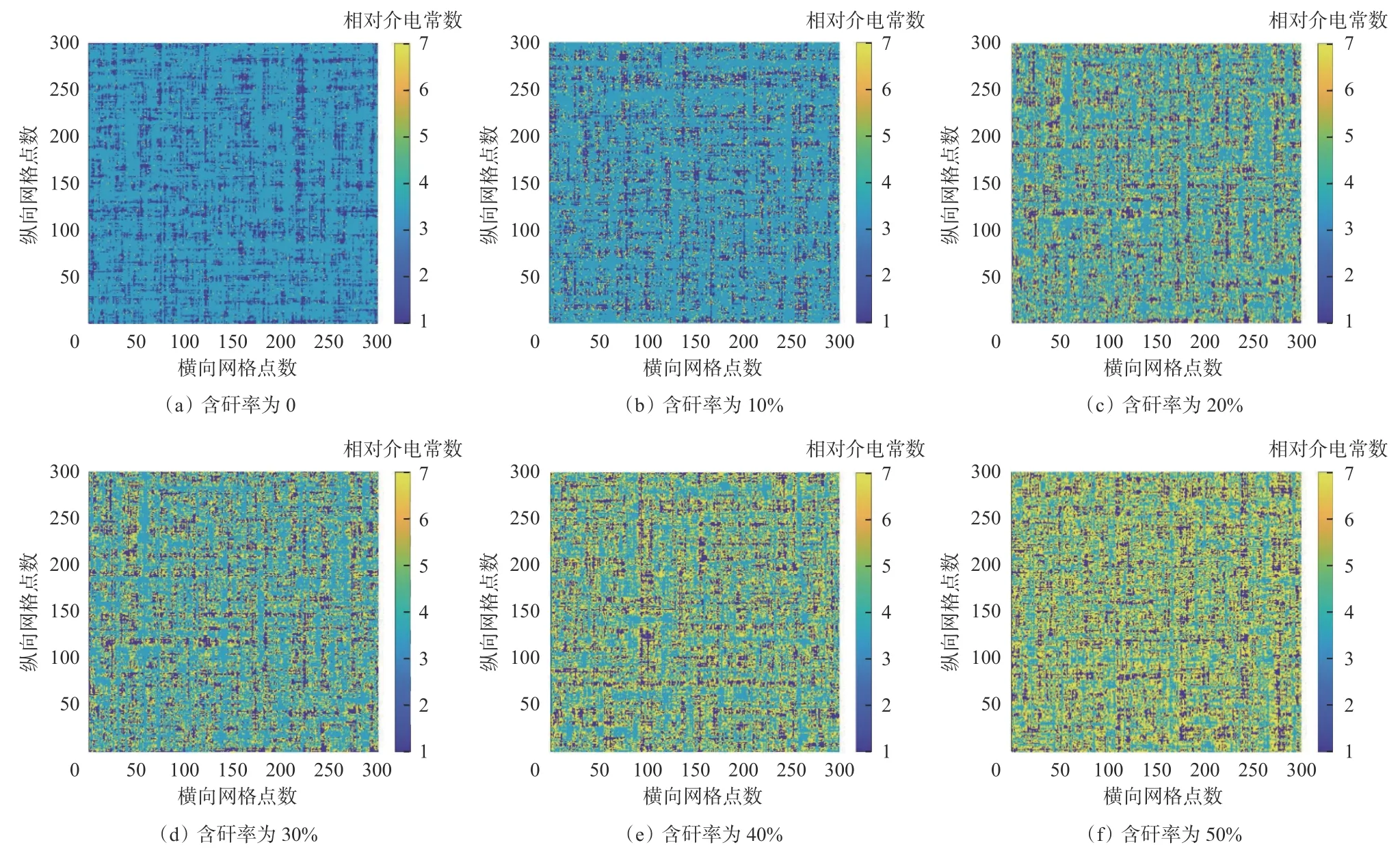
图8 不同含矸率的煤矸多相离散随机介质模型Fig. 8 Multiphase discrete random medium model of coal gangue with different gangue content

使用时域有限差分法对煤矸多相离散随机介质模型进行电磁波正演模拟，通过解算麦克斯韦方程，得到透射波时域波形，如图9所示。

图9 透射波时域波形Fig. 9 Time domain waveforms of transmitted wave

从图9可以看出：透过含矸率为0的煤矸模型的电磁波信号最先达到峰值，且信号幅值最高；透过含矸率为50%的煤矸模型的电磁波信号最后达到峰值，且信号幅值最低；随着含矸率升高，透射电磁波的信号幅值依次降低，并且透射时间依次延长。由于矸石的相对介电常数远高于煤和空气，所以含矸率升高使煤矸混合物整体的等效介电常数升高。这在一方面会引起介质整体的电导率增加，而电磁波在介质中的损耗与电导率呈正比，故电磁波在含矸率越高的模型中损耗越大，信号幅值越低；另一方面会引起介质的折射率增加，电磁波的传播速度与折射率成反比，故电磁波在含矸率越高的模型中透射时间越长。含矸率为40%的模型与含矸率为50%的模型的峰值时间和信号幅值差异不大，这是由于含矸率达到一定值后，模型整体的相对介电常数趋于岩石的相对介电常数。工程上含矸率通常控制在10%～30%，而从图9可看出，在此区间电磁波的传播特性差异明显，因此本方法具备实际应用条件。