基于改进哈夫曼编码的Haar 小波WSN 数据压缩算法
2023-11-10夏长权徐思韵张剑云时壮壮朱金荣
夏长权,徐思韵,张剑云,时壮壮,朱金荣
(1.扬州大学物理科学与技术学院,江苏扬州 225000;2.扬州大学信息工程学院,江苏 扬州 225000)
无线传感器网络节点的主要部署区域为地理环境比较复杂的地方,而且节点的供电方式为电池供电,一旦节点能量耗尽,更换起来十分麻烦。因此,如何有效节能成为近几年无线传感器网络领域研究的热点。无线传感器网络节点在硬件上的能量消耗主要在传感器、处理器和无线通信三大模块上。但是,随着集成电路工艺的进步,处理器和传感器模块的功耗变得很低,绝大部分的能量消耗在无线通信模块上,传输1 bit 数据所消耗的能量大约相当于执行1 000 条CPU 指令消耗的能量[1]。因此,通过减少传感器节点之间的数据传输量来降低无线通信模块负载量可以大大节省传感器节点能量,达到降低网络能耗的目的。
目前无线传感器网络中常用的数据压缩算法主要可以分为两大类:有损压缩算法和无损压缩算法。有损压缩算法主要有离散余弦变换和小波变换[2],无损压缩算法主要有游程编码和哈夫曼编码[3]。有损压缩算法在数据压缩率方面具有一定的优越性,但是在数据恢复方面显得略为逊色,而无损压缩算法则正好相反。关于有损压缩算法,前人已经做了一些相关的改进,比如文献[4]提出了一种可以动态改变压缩位率的小波压缩算法,文献[5]提出了一种减少数据空间相关性的分布式小波压缩算法。但是,这些文献中提到的压缩算法均不能获得较高的数据压缩率。
为了完全覆盖监控区域,无线传感器网络节点一般部署比较密集,同一节点在不同时刻采集到的数据和不同节点在同一时刻采集到的数据具有极大的相似性[6]。这种相似性被称为时间相关性和空间相关性,正是这些相关性为数据的有效压缩提供了依据。这里依据传感器节点采集到的数据具有时间相关性和空间相关性,提出一种基于曲线拟合的小波压缩算法,并采用网络仿真软件,对提出的数据压缩算法进行仿真实验,选取的评价指标为压缩比和均方误差。仿真结果表明,该算法在对无线传感器网络采集到的数据进行数据压缩时具有较高的压缩比,能够有效地减少数据传输量,并且在数据恢复方面精度较高。
1 小波数据压缩
1.1 曲线拟合
由于同一传感器节点在不同时刻采集到的数据为离散时间序列,为了便于研究,这里采用曲线拟合的方法将离散信号转换为连续信号。常用的曲线拟合方法有最小二乘法、基于RBF 的曲线拟合法和三次样条曲线拟合法[7]。其中,最小二乘法逻辑推导比较简单,并且具有计算量小的特点,被广泛应用在多项式曲线或直线的拟合问题上。使用最小二乘法进行曲线拟合时,需要注意选取合适的匹配函数模式。
传感器节点采集的温度数据如图1 所示,纵坐标是用十进制表示的温度数据值,横坐标是选取的温度数据样本数。由图1 可以看出,传感器节点采集的数据呈现多项式的变化规律,因此,可以用式(1)多项式进行拟合:

图1 节点采集的原始数据分布
为了使拟合后的数据与原始数据之间误差尽可能小,这里选取了三种不同次数的多项式进行拟合,并分析各自的误差情况。其中,误差大小用误差平方和来衡量,其定义如式(2)所示:

图2 不同次数多项式拟合结果
误差平方和是评价一条曲线拟合效果好坏的重要指标,误差平方和越小,则该曲线的拟合效果越好;误差平方和越大,则该曲线的拟合效果越差。使用上述三种不同次数的多项式拟合结果如表1所示。

表1 不同次数多项式拟合误差
从图2 以及表1 可以看出,用最小二乘法进行数据拟合时,拟合结果与实际数据之间存在一定误差,并且选取的多项式次数较小时,误差较大;选取的多项式次数较大时,误差较小。这是因为选取的多项式次数较小时,各数据点之间距离较远,误差也就较大。在该实验中,多项式拟合的误差平方和随着拟合多项式次数的增加而逐渐减小,在多项式次数选取为十五时,误差最小,拟合曲线更接近实际数据,拟合更准确。
1.2 小波压缩
传感器节点在不同时刻采集到的数据具有极大的相似性,处理这些数据常用的方法有傅里叶变换、K-L 变换等。随着研究的深入,越来越多的变换域算法开始应用于无线传感器网络数据压缩,如离散余弦变换和小波变换等。小波变换数据压缩算法相较于其他的变换域数据压缩算法有着分解效果更好和运算结构单一的特点[8-9]。
Haar 小波基函数是小波变换中最简单的基函数,它的函数集由多个分段函数组成,并且这个分段函数是常值函数,在区间[0,1)上一段为1,一段为0。Haar 小波变换的过程是求均值和差值的过程[10],对于长度为2n的信号sn={sn,l|0 ≤l<2n},将求均值和差值应用到a=sn,2l,b=sn,2l+1(l=0,1,…,2n-1-1)中。记,则多级Haar 小波变换的分解过程和重构过程可用图3 表示。

图3 小波变换的分解和重构过程
利用上述Harr 小波变换算法对传感器采集的数据进行三次小波分解后的空间-频率结构如图4 所示。小波变换具有大部分有用信息集中在低频系数,而小部分细节信息集中在高频系数的特点[11]。在图4 中,经过拟合后的信号被分为四个部分,其中,H0、H1、H2 是高频部分,L2 是低频部分。对高频部分的系数进行阈值处理,将绝对值小于阈值的高频系数设置为零,绝对值大于阈值的高频系数保持不变。为了将阈值处理后的小波系数进行编码压缩,首先将小波系数整数化,采用的取整方法是向下取整法。假设某小波系数为3.671 2,则向下取整后为3。要获取传感器采集的数据的主要信息只需存储取整后的小波系数即可,而通过算术编码的方法存储小波系数在提高数据恢复准确率的同时还可以进一步压缩存储空间。

图4 信号被分解后的频率结构
2 Haar小波系数的编码
对进行Haar 变换后的小波系数进行编码,需要在保证数据质量的前提下提高压缩率,而哈夫曼编码正好满足这一条件。哈夫曼编码是根据信源中各符号出现的概率进行编码,出现概率大的符号使用较短的码字,出现概率小的符号使用较长的码字[12]。举例来说,假设某信源产生五种符号u1、u2、u3、u4 和u5,它们各自的概率分别为P1=0.4,P2=0.1,P3=P4=0.2,P5=0.1。编码过程:进行编码前首先将各符号按照概率由大到小的次序排队,编码时,从最小概率的两个符号开始,将上支路设为0,下支路设为1。然后将两个已编码支路的概率相加,并重新排队。以此类推,不断使用上述方法,直到相加概率为1 时结束。此时,按照每个符号的支路路径可以得出各自的编码结果。u1、u2、u3、u4 和u5 的编码结果即为000101011011。
为了存储方便同时进一步压缩存储空间,对经过传统哈夫曼编码后的结果按一定位数转化为十进制数后再存储,这里选取的数据位数为8 位,不足8位的在前面用0 补齐,则上述假设中的最终编码结果为2111,进一步压缩了数据位数。
改进哈夫曼编码算法的实现过程:首先,统计原始数据中各字符出现的概率,然后,将这些字符按照出现概率的降序排列,并依此建立哈夫曼树,将哈夫曼树的索引结果存入各字符的编码结果中,最后,使用进制转换将一定位数的二进制编码转换为十进制编码即为最终编码结果。其算法实现流程图如图5 所示。
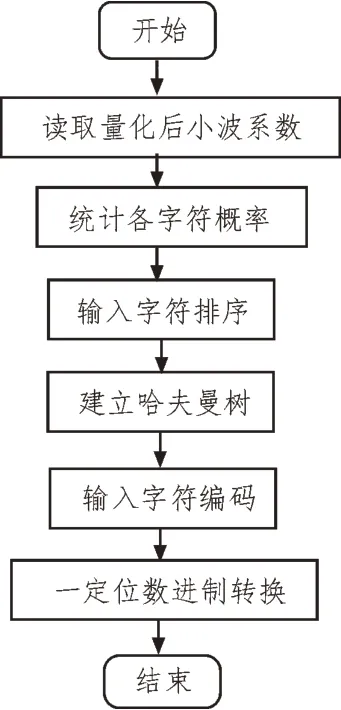
图5 哈夫曼算法实现流程图
3 实验与分析
该实验采用的是英特尔伯克利实验室54 个传感器中的3 个在不同时刻采集到的数据,这些传感器分布在实验室的不同位置,每个传感器每隔31 s采集一次数据,采集的数据包括温度、湿度、光照和电压[13]。提取其中的温度数据作为数据源进行实验,图1 是原始温度数据与样本数的关系图,由图1 可以看出节点采集的温度数据呈逐渐下降的趋势。
3.1 比较不同算法的压缩比
将以上3 个不同传感器采集到的数据保存为不同的txt文件,分别命名为1.txt、2.txt、3.txt。对这些txt 文件采用不同的压缩算法进行压缩测试,测试环境为Matlab2016a,测试结果如表2 所示。

表2 不同压缩算法压缩比
定义压缩比概念为:
由表2 可以看出,改进算法的压缩比最大,可以获得平均7.09 的压缩比。相比小波压缩算法以及哈夫曼编码方法,改进算法提取了两种算法的优势之处,并对编码后的结果进行了二次压缩,因此具有相对较高的压缩比。
3.2 比较不同算法的均方误差
均方误差反映了重构数据与原始数据的相似程度,均方误差越小表明重构的数据越精确。
均方误差的概念如下:设原始信号S={X(t)|t=1,2,3,…,k},S*={X*(t)|t=1,2,3,…,k}为一个估计信号,则该估计信号的均方误差如式(4)所示。
表3 是三种不同压缩算法的均方误差。

表3 不同压缩算法均方误差
由表3 可以看出,三种算法的均方误差里哈夫曼编码算法的误差最小,这是因为哈夫曼编码是无损数据压缩技术,而哈夫曼编码算法的误差主要来源于曲线拟合时的误差。小波压缩算法是有损数据压缩技术,其误差来源有曲线拟合时的误差、小波系数阈值处理以及取整时的误差。因此,小波压缩算法和改进算法的误差基本持平,稍大于哈夫曼编码算法。在对数据恢复精度要求不高的情况下,使用改进算法更为合适,因其具有更大的数据压缩比。
4 结论
针对无线传感器网络在数据采集时存在的大量冗余数据问题[14-16],提出了一种基于改进哈夫曼编码的Haar 小波WSN 数据压缩算法。首先对这些数据进行线性拟合,然后经过小波变换提取出相应的小波系数后,采用哈夫曼编码的方式将原始数据转换为一串二进制编码。进一步地,为了达到更好的压缩效果,将这些二进制编码串按一定位数转换为十进制编码串。仿真实验结果表明,相较于传统小波压缩算法数据压缩率提高了大约34%,而均方误差基本持平。该算法可以应用于对数据压缩比要求比较高的场景,但是由于所提算法在进行线性拟合时采用的是传统的拟合方法,拟合精度还有待提高。未来可考虑与神经网络结合,进一步提高拟合精度,进而减小均方误差。
