固本探源,突破瓶颈,提高效益
——基于“三新”背景下的高考一轮复习策略
2023-11-10江苏省宿迁中学王嘉琨
江苏省宿迁中学 王嘉琨
在新教材(人民教育出版社2019年国家教材委员会专家委员会审核通过)、新课程(《普通高中数学课程标准(2017年版2020年修订》)、新高考的“三新”背景下,高考坚持核心素养导向,倡导数学关键能力,注重数学创新意识与创新应用.基于“三新”背景下的高考数学一轮复习,要切实贯彻与落实高考改革的考查要求,因此,综合高效复习就变得尤其重要.
1 回归高中教材,探究知识本源
新高考不再有《考试大纲》的局限与限制,高中数学教材成为高考的主要依据之一.通过近几年的新高考数学试卷可以发现,高中数学教材是高考数学试题的命题来源与知识基础,是高考能力题的立足点与生长点.高考数学试题就是对高中数学教材的横向优化,形成知识的联系与交汇;同时也是高考中数学教材的纵向深化,渗透核心素养,考查数学能力.
例1〔人教版《数学》(选择性必修二册)第94页练习第2题〕证明不等式:x-1≥lnx,x∈(0,+∞).
以上重要不等式及其他一些相关的结论,如(1)ex>x+1(x≠0),(2)lnx
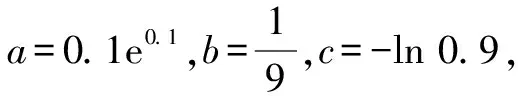
A.a C.c 综上分析,可知c 因而,高考数学一轮复习教与学的过程中,一定要紧紧抓住教材,任何阶段都不能脱离教材,通过对教材中的基础知识、基本方法与典型例(习)题加以总结与提炼,进而形成数学知识“串”,构建数学问题“链”,从而更加深入地探究高考数学命题的本源,全面开展一轮复习与教学. 合理钻研近年新高考数学真题,切实领会高考试题的设计思路、考查要点与考查意图等,从中探寻高考命题的变化、创新与规律,更好地服务高考数学复习的教与学,进而合理改变教与学过程中由全面覆盖、盲目备考转向抓住主干、精准备考. A.tan(α+β)=1 B.tan(α+β)=-1 C.tan(α-β)=1 D.tan(α-β)=-1 分析:根据题设条件,结合三角函数关系式的结构特征,先利用两角和与差的公式加以展开,使得复杂角转化为简单角,然后结合变形所得的三角函数关系式,利用两角和与差的公式进行“逆向”转化,再进行三角函数式的变形与求值. 整理,可得sinαcosβ-cosαsinβ=-cosαcosβ-sinαsinβ,即sin(α-β)=-cos(α-β). 所以tan(α-β)=-1.故选择答案:D. 点评:三角函数问题,一直是新高考中考查的一个基本知识点.常规方法是利用三角函数中相关的公式,如三角恒等变换公式、辅助角公式、和差化积公式与积化和差公式等加以变形与转化,或者利用特殊值、整体验证等思维方式来处理. 高考复习不是新授课,要精心挑选典型例题与配套的习题,注意总结解题规律,并从中提炼出对应的数学思想方法,使学生能举一反三,融会贯通,触类旁通,形成从数学基础到数学综合,从解题模仿到变式拓展,从变式练习到创新应用的层层递进,多层面、多视角、螺旋式步步提升,真正有效提高高考数学复习效益. 分析:根据题设条件与所求结论中a,c具有轮换性,采用两边长相等的特殊化处理,通过余弦定理确定对应角的余弦值,结合同角三角函数基本关系式与二倍角公式加以变形与转化,进而得以求值.本题可以借助“一题多解”的方式继续展开,这里从略,在此基础上还可以进一步变式与拓展. 点评:由解三角形问题,联想到圆锥曲线与平面几何问题,产生良好的效益.结合高考数学真题,探究高考命题变化与命题改革,巧妙贯彻数学创新与数学应用,渗透创新应用场景与数学文化,结合典型数学问题进行变式训练与拓展创新,回避题海战术,全面提升高考数学复习效益. 2022年的新高考数学试卷中出现了南水北调工程、地方性疾病与当地居民的卫生习惯、中国古代建筑、流行病学调查等数学文化创新问题,与新课标所强调的“创新性、应用性”相吻合.随着新高考的逐步深入,社会实践的应用、数学文化的渗透等应用型问题情境已经成为高考的一类必考题. 例4某舰队为庆祝军舰入列10周年,舰队官兵举行了盛大的庆祝仪式,在舰上布置了彩旗(如图1),挂彩旗的绳子长100 m,绳子固定在舰岛上高度均为16 m、相距28 m的两处舰桥的AB和CD的端点A和C处,并在甲板上E处绷紧,已知绳子和两舰桥在同一平面内,则甲板上E点到舰桥AB的距离为______m. 图1 分析:基于现实生活中应用场景,渗透数学文化,理解题目条件,合理构建平面直角坐标系,抓住两线段和为定长,结合椭圆的定义,正确构建相关点满足的轨迹方程,进而得以解决实际应用问题. 解析:如图2所示,以AC所在直线为x轴,AC的垂直平分线为y轴建立平面直角坐标系,则有A(-14,0),C(14,0),B(-14,-16),D(14,-16). 图2 依题可知|AE|+|CE|=100>28. 点评:新高考背景下,中国古代数学典籍与文明创造、现代科学发展与技巧、社会进步与生活场景等各方面的创新应用都巧妙融入到了高考数学试卷中,以各种形式融合相关数学知识加以应用,巧妙达到渗透创新意识与创新应用的目的. 在新教材、新课程、新高考的“三新”背景下,合理回归高考数学教材,扎根数学基础知识,构建数学体系结构,结合高考数学真题,探究高考命题变化与命题改革,贯彻数学创新与数学应用,渗透创新应用场景与数学文化,结合典型数学问题进行变式训练与拓展创新,回避题海战术,进而全面提升高考数学复习效益.
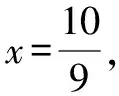
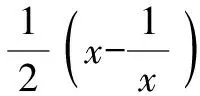
2 钻研高考真题,挖掘命题规律


3 强化变式训练,提高复习效益
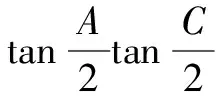
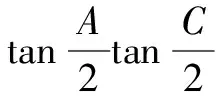

4 渗透数学文化,突破应用瓶颈