函数奇偶性,解题妙应用

江苏省海安高级中学 许 陈

函数的奇偶性是函数的基本性质之一,反映了函数图象的对称性特征,同时兼备函数自身中“数”与“形”的双重性质,是研究数学的一个基本工具,也是历年高考数学试卷中比较常见的一个重要知识点.同时,函数的奇偶性又可以很好地交汇与融合函数的基本知识,以及数学中的其他基本知识点,是充分体现高考“在交汇知识点处命题”指导思想的重要平台,倍受各方关注.

1 结合奇偶性确定函数值

直接利用函数的奇偶性求解函数值及其相关应用是比较常见的一类问题,难度比较小,关键是合理应用函数奇偶性加以分析、转化与处理.

例1已知函数y=f(x)是R上的奇函数,当x>0时,满足f(x)=x2-2x-1,则f(-3)的值是______.

分析：结合奇函数的定义,合理构建关系式f(-x)=-f(x),取特殊值代入得到f(-3)=-f(3),即可求解.

解析：由于函数y=f(x)是奇函数,则利用函数的奇偶性的定义,可知

f(-3)=-f(3)=-(32-2×3-1)=-2.

故填答案:-2.

点评：以上问题还可以先由f(3)=32-2×3-1=2,再结合函数y=f(x)是奇函数,可得f(-3)=-f(3)=-2.正确把握函数的奇偶性,以及对应的自变量与函数值之间的关系,是分析与解决此类问题的关键所在.

2 结合奇偶性确定函数解析式

直接利用函数奇偶性的定义,得到所对应的函数解析式之间的关系f(-x)=-f(x),或f(-x)=f(x),前者是奇函数的基本性质,后者是偶函数的基本性质,进而通过已知函数解析式的变形与转化,可以很好地确定一些相关函数的解析式问题.

例2已知函数f(x)是奇函数,且当x>0时,f(x)=x|x-2|,求当x<0时,函数f(x)的解析式.

分析：结合奇函数的定义,得到关系式f(-x)=-f(x),通过已知解析式的合理转化,确定x<0时f(x)的解析式.

解析：当x<0时,-x>0,则有

f(-x)=-x|(-x)-2|.

又因为f(x)为奇函数,所以f(x)=-f(-x)=x|(-x)-2|=x|x+2|.

故当x<0时,f(x)=x|x+2|.

点评：利用函数奇偶性的定义来解决一些相关的函数解析式问题时,关键要注意函数自变量的正负取值情况以及变量之间的对应关系,合理替代,巧妙代换,通过整体思维、对应思维来分析与应用,从而解决一些涉及函数解析式以及对应的应用问题.

3 结合奇偶性判断函数图象

利用函数基本性质奇偶性,通过结构特征来判断与之对应的函数图象的对称性问题,是函数奇偶性的一个非常直观形象的应用,可以便捷且直观地从函数图象来确定与函数奇偶性对应的性质[1].

例3函数f(x)=x·ln|x|的图象可能是( ).

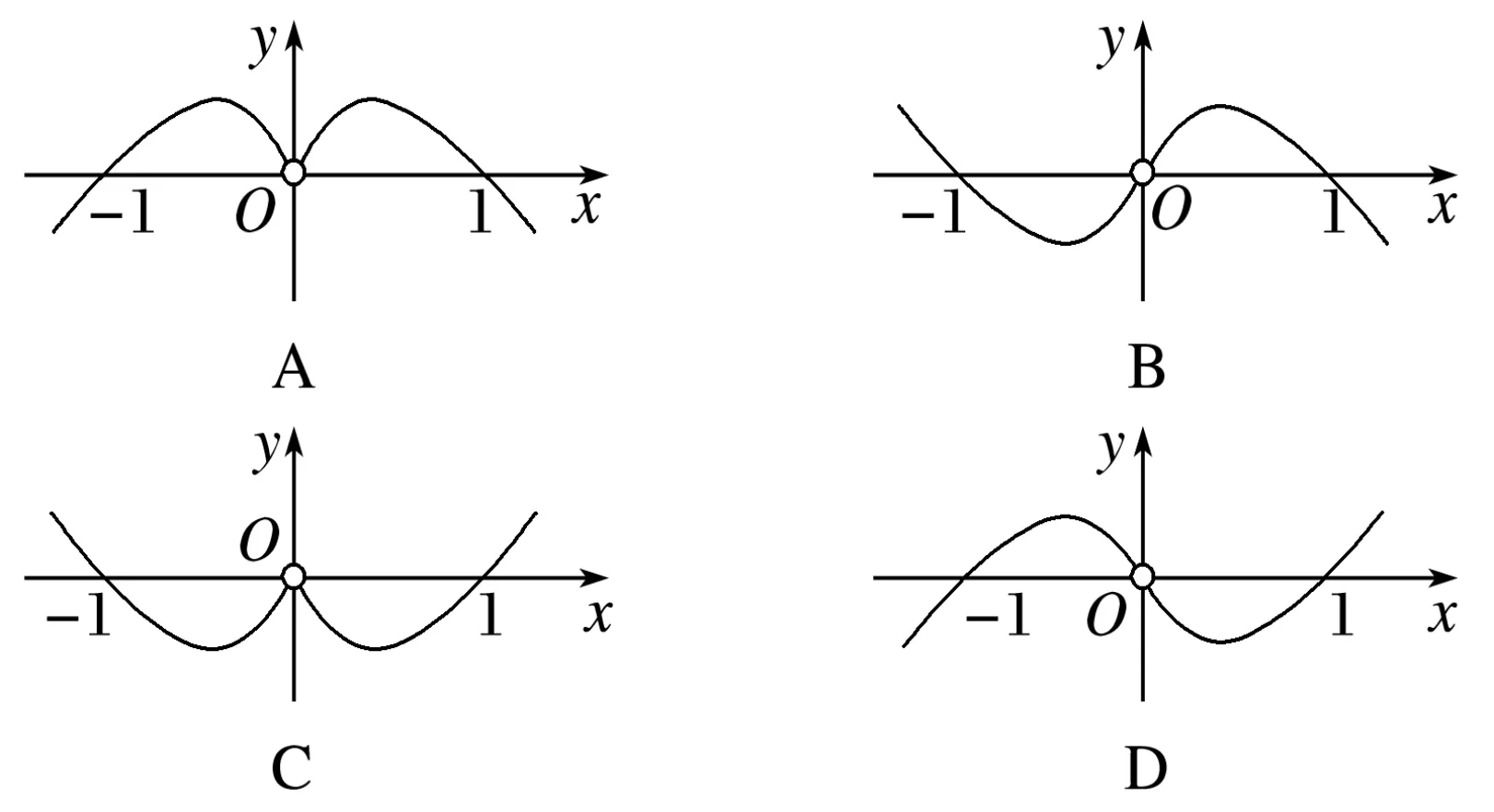
分析：结合条件中给出的函数解析式来分析与判断已知函数的奇偶性,通过函数的奇偶性所对应的图象的对称性来分析排除相关的选项;在此基础上利用特殊点进一步合理排除相关的选项,巧妙判断.

解析：对于函数f(x)=x·ln|x|,由于f(-x)=-x·ln|-x|=-x·ln|x|=-f(x),则知函数f(x)=x·ln|x|是奇函数,可以排除选项A,C;

故选择答案:D.

点评：具体判断函数的图象以及相关问题时,可以借助函数的奇偶性来判断整个函数图象的对称性问题,而具体的一些细节,还要综合特殊函数值的确定、函数的极值与最值以及其他的一些基本性质与特征来综合处理.

4 结合奇偶性求解最值

函数的奇偶性具有一定的对称性与反射性,由此可以通过函数图象的对称性与对应的函数值来解决一些与之相关的函数最值问题,从而判断一些与最值有关的函数问题[2].

例4若f(x)和g(x)都是奇函数,且F(x)=f(x)+g(x)+2在(0,+∞)上有最大值8,则在(-∞,0)上F(x)有( ).

A.最小值-8 B.最大值-8

C.最小值-6 D.最小值-4

分析：先根据条件确定函数关系式f(x)+g(x)的最大值,结合函数f(x)和g(x)都是奇函数,可以确定函数f(x)+g(x)在(-∞,0)上的最小值,进而确定函数F(x)在对应区间上的最小值问题.

解析：根据题意可知函数f(x)+g(x)在(0,+∞)上有最大值6.

又因为函数f(x)和g(x)都是奇函数,所以函数f(x)+g(x)是奇函数,则函数f(x)+g(x)在(-∞,0)上有最小值-6,即函数F(x)在(-∞,0)上有最小值-6+2=-4.

故选择答案:D.

点评：在实际求解一些相关函数的最值问题时,经常要借助函数在相应区间上最值的确定,以及函数奇偶性的判定,从而综合交汇,创新应用.当然,具体解决问题时,可以借助特殊函数(如一次函数等)来直观分析,更加简单快捷来处理此类函数最值问题、函数对称性问题等.

5 结合奇偶性求解不等式

在解决一些抽象函数对应的不等式问题时,经常要借助函数的奇偶性等基本性质及结构特征来巧妙转化,进一步确定所要求解的不等式,这是解决问题的关键所在.在一些具体应用中,经常要与函数的解析式、单调性以及其他的相关知识加以交汇与融合,从而实现问题的创新性、综合性与应用性[3].

例5已知函数f(x)=x3-2x+ex-e-x,其中e是自然对数的底数,若f(a-1)+f(2a2)≤0,则实数a的取值范围是______.

分析：根据函数奇偶性的定义来确定函数f(x)是奇函数,为进一步的变形与转化相应的不等式提供条件,利用求导处理以及基本不等式的应用来确定函数的单调性,从而巧妙转化不等式,进而通过解一元二次不等式来确定参数的取值范围问题.

解析：由函数f(x)=x3-2x+ex-e-x,可得f(-x)=(-x)3-2(-x)+e-x-ex=-x3+2x-ex+e-x=-f(x).

又x∈R,所以f(x)=x3-2x+ex-e-x是奇函数.

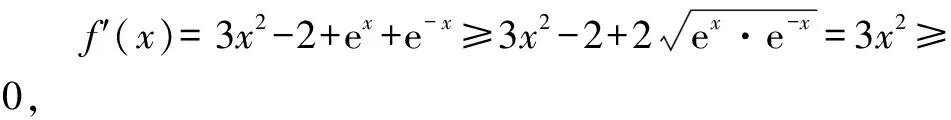
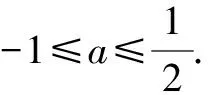
点评：此题中,巧妙融入高次函数、指数函数以及抽象函数类型,融合函数的奇偶性与单调性、导数及其应用、基本不等式以及二次不等式的求解等相关内容.其中确定函数的奇偶性是关键,为进一步的变形与转化指明方向,是解决问题的一个重要切入点.

其实,历年高考数学试卷中,往往离不开对函数奇偶性的考查,有时直接设置相关题目,有时隐含在其他数学问题中,形式各样,变化多端.此类涉及函数奇偶性的问题通常以小题(选择题或填空题)为主,难度中等及偏下,有时单独考查函数的奇偶性,有时将函数相关概念与与函数的奇偶性加以综合,有时还融入其他模块知识,实现知识点间的交汇与融合.抓住函数奇偶性的定义及对应的函数的图象性质,合理总结规律,巧妙综合,创新应用.