动中明定 定中求变——例谈解题教学中如何引导学生深度学习

四川省攀枝花市第十二中学校 李 丹 张勇辉

运动变化是数学学习中重要的思想方法之一,很多数学问题都呈现出“动中有定、动定相倚”的特点,教学中教师若能敏锐抓住这些特点,从“动”中寻找规律,从“定”中寻求突破,引导学生深度学习,对夯实学生数学基础、开阔数学思维、提升解题能力将大有裨益.

下面,笔者从一道圆锥曲线试题的解题探究说起,谈谈解题教学中如何巧抓“动定关系”,引导学生进行深度学习.

1 试题呈现,条分缕析

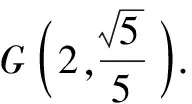
(1)求椭圆C的标准方程.

(2)椭圆C的上、下顶点分别为点M和N,动点A在圆x2+y2=1上,动点B在椭圆C上,直线MA,MB的斜率分别为k1,k2,且k1=5k2.

(ⅰ)证明:N,A,B三点共线;

(ⅱ)(略).

这是临近高考的一次统测中的解析几何压轴题.笔者所教授的班级属于中等层次,多数学生第(2)问只能草草书写一些方程,蹭一些步骤分.一个中等难度的试题成了本班学生的难题.

对于第(2)(i)问,从试题条件和结论分析,在前提条件下,“k1=5k2”是“N,A,B三点共线”的主要条件,条件与结论中的“动”“定”关系如表1.

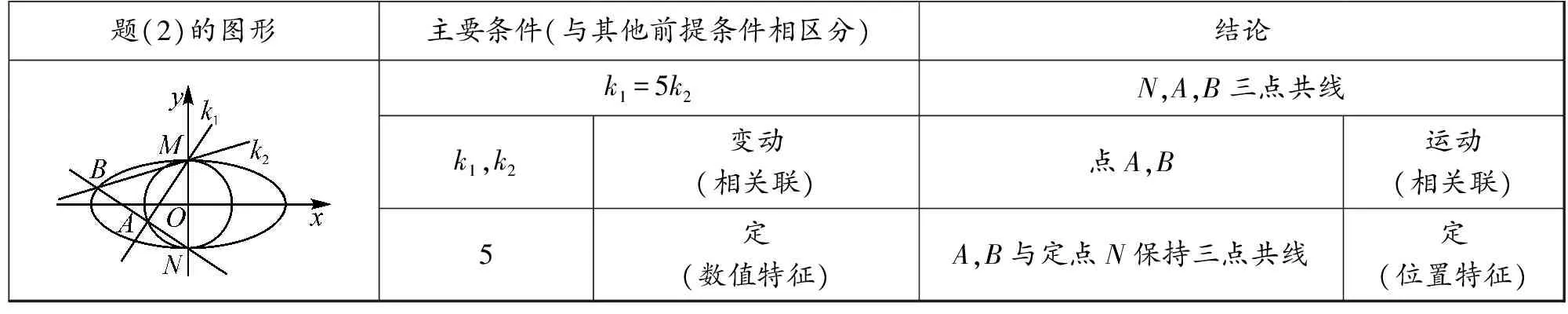
表1 条件与结论中的“动”“定”关系

因此,只要抓住主动点A,设出直线MA的方程,解出点A的坐标,同法解出从动点B的坐标,再比较直线AN,BN的斜率,问题便得以解决.第(2)(i)问的解答通法如下.

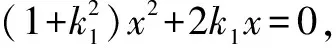
学生失分的主要因素有以下三个方面:(1)学生普遍对解析几何大题有一种畏惧之心,长期的碰壁使其逐渐降低了得分的心理预期,不少学生抱着绕着走的心态;(2)圆锥曲线相关知识方法、重要二级结论等储备不足,对一些条件不熟悉,不知如何破题,缺乏题感;(3)也是最重要的一点,虽然做过不少题,但缺乏深度学习,解题方法零散、碎片化,不成系统,下次遇到同类型的问题仍然重复犯错,解题自信心屡受打击,从而丧失信心.

2 逆向思考,存疑设问

对于这道试题的学习,如果到此为止,学生的解题思维和能力仍然得不到提高,因此有必要把探究引向深入.评讲之后,笔者问了学生两个问题:条件“k1=5k2”中的定值为什么恰好是“5”?这个“5”从何而来?立马引得了几个学生的附和,之后学生们陷入沉思.笔者将这些问题留给他们课后研讨,准备第二天针对此题上一堂探究课.

3 展开实验,初步探究

为了探究“5”的来由,笔者制作了几何画板课件,便于随时改换条件进行动态研究和展示,以数学实验的方式展开探究之旅.以下是课堂上的一些片段.

片段一：

师:谁能告诉大家,这个“5”从何而来?

生甲:我认为,这个“5”就是椭圆方程中的a2=5.

师:能给个理由吗?

生甲:说不太清楚,直觉.

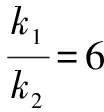
图1

片段二：

师:能确保你们的运算是正确的吗?

生丁:能,我和同学丙都算过两遍.

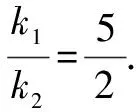
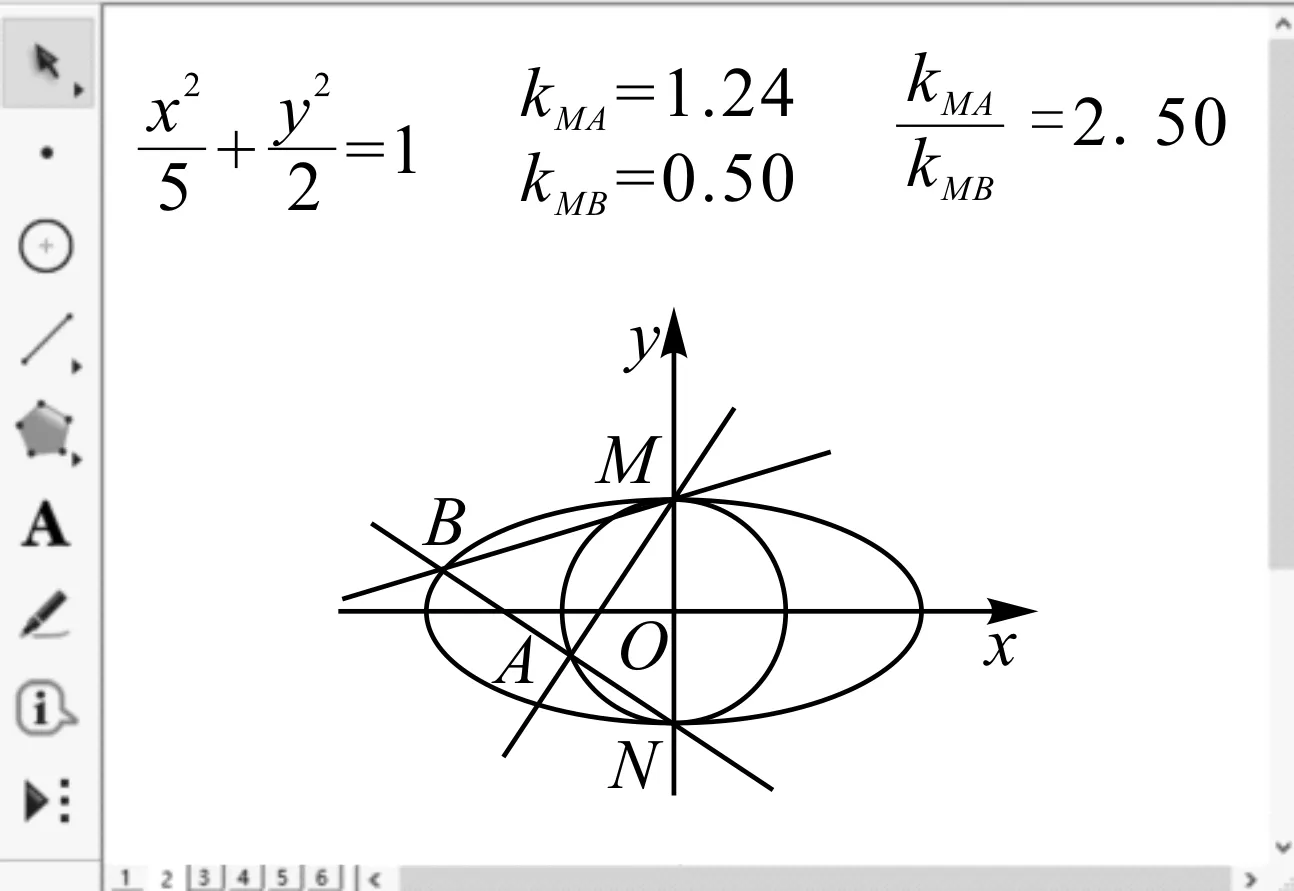
图2

片段三：

师:通过前面的探究,我们有必要把前面讨论的重点问题重新归结一下,可以得到以下命题.

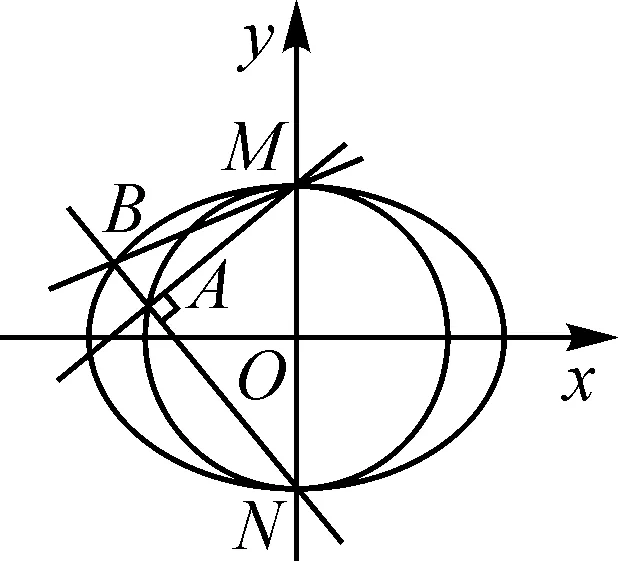
图3

(把时间留给学生,思考该如何证明,教师巡视.)

师:同学们如果仿照通法证明,运算量将非常大!有些同学已经开始怠工了.我发现同学乙找到了简洁的证明方法,请他给大家展示一下.

生乙:由题意,得

①

②

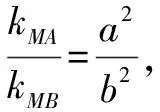
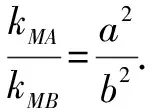
师:多么简洁!(全班鼓掌!)同学乙用到了我们以前学过的关于椭圆的一个重要的二级结论.双曲线也有类似的性质,我们再一起回顾一下:

师:圆锥曲线的一些重要的二级结论在解决相关问题时非常有用,请同学们多总结,多运用,这样一定能提高解题能力!

4 深度探究,精彩纷呈

针对本试题的课堂探究到此为止,但意犹未尽.作为课后作业,笔者要求学生模仿本题的命题思路及证明方法,命制一些类似的新命题.以下是学生的部分作品:

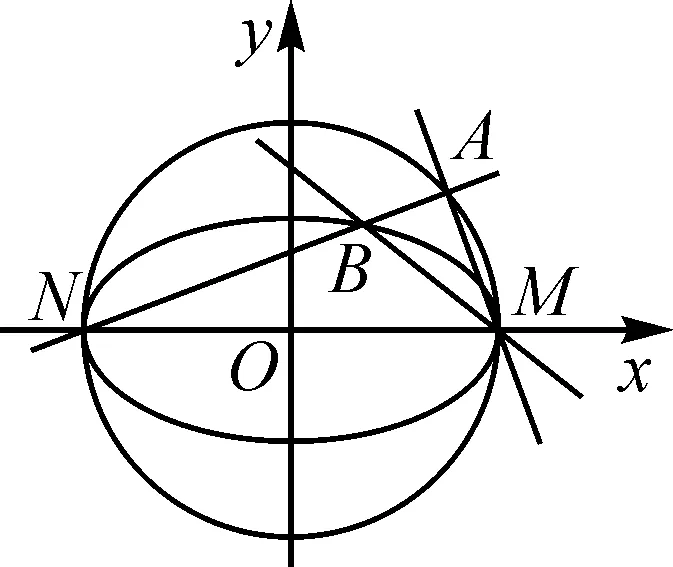
图4

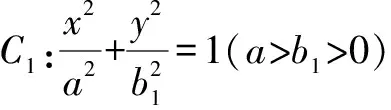
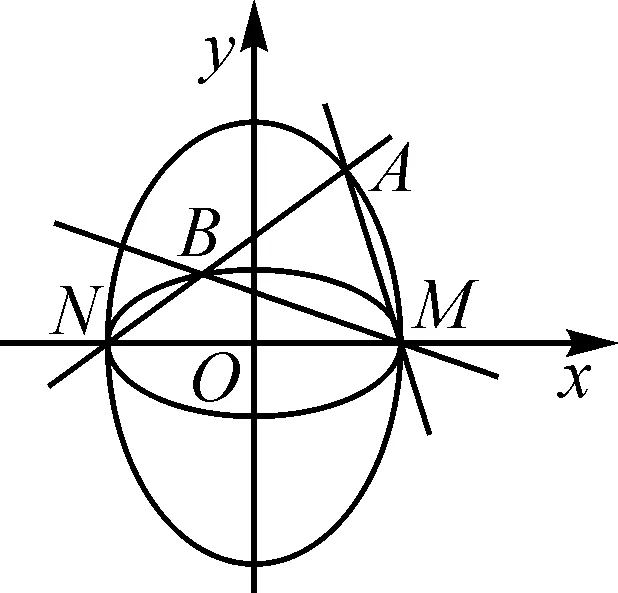
图5

图6

5 教学反思,启迪智慧

(1)本课从试题条件“k1=5k2”中的“动”与“定”——k1,k2的关联变动和定值5的分析入手,明辨出“5”是“N,A,B三点共线”的决定性因素.问题“为什么恰恰是5?5从何而来?”则挠到了学生思维的“痒痒处”,激起了共鸣,激发了探究的热情,引出了一系列真实有效的探究.

(2)探究的过程符合认知规律,经历了验证、试错、证伪、猜测、论证等过程,从特殊到一般,从简到繁又以简驭繁,用一个二级结论辅助证明归纳出的命题,不仅避免了繁杂的运算,还将探究引向深入.

(3)拓展探究把整个探究过程推向一个新高度.学生从一般性命题的简洁证明中,找到了与其他背景知识的契合点,有效迁移,命制出了崭新的命题.若将这些命题作为“题源”,将字母系数数值化,再更换背景,又能命制出成串的数学试题!

(4)本课运用《几何画板》辅助教学,以数学实验的方式展开探究之旅,形象地展示了问题中的“动”“定”关系,为快速证伪、猜测验证提供了帮助.

6 结语

高中数学各知识板块,特别是函数、数列、三角、向量、立体几何、解析几何大量问题中都蕴含着“动定关系”.通过动与定的转化,加深对问题本质的理解,培养思维的深刻性.对动与定的关系的观察,便于寻求规律,培养思维的灵活性与广阔性.灵活处理数学中动与定的关系,动中明定,定中求变,是创造性思维的一个体现.

深度学习具有以下特征:浅层加工与深层加工的统一,多重理解与整体建构的统一,掌握知识和提升能力的统一,自主学习与合作学习的统一.教师只有熟悉这些特征,才能有效制定策略,设计实施路径,把学生的学习和探究引向深入.

《普通高中数学课程标准(2017年版2020年修订)》在阐述高中数学的课程目标中指出,要让学生获得“四基”,提高“四能”,发展“数学核心素养”.教师不仅要把这些理念深深植根于脑海,更重要的是践行于每一次数学活动、每一个教育细节中,而引导学生深度学习就是很好的途径之一.安于心而敏于行,点滴浸润,长期坚守,方能见穿石之效,收尺寸之功!