粒子冲击及其辅助钻齿破岩规律研究

2023-11-09祝效华刘伟吉罗云旭阳飞龙

西南石油大学学报(自然科学版) 2023年5期

祝效华，何灵，刘伟吉，罗云旭，阳飞龙

西南石油大学机电工程学院，四川成都 610500

引言

中国油气资源需求量极大，随着浅层油气储层资源渐近枯竭，深井、超深井及复杂难钻地层的勘探与开发成为研究重点[1]。随着井深增加，岩石硬度增大，研磨性增强，可钻性降低。这些因素导致钻头易磨损，转速降低，进而导致钻具易损坏，钻井成本高，钻进周期长，严重制约深部油气藏的高效低成本开采。因此，亟需探索极具突破性的破岩提速新方法[2]。目前，钻井破岩新技术主要有等离子体破岩、激光破岩、超声波及热能破岩和粒子冲击钻井（Particle Impact Drilling，简称PID）等[3]，但前3种技术尚处于理论研究和实验模拟阶段，还不能投入实际生产中，粒子冲击钻井技术经过近十几年的快速发展已有应用[4]。

粒子冲击钻井是用粒径为0.5∼5.0 mm 且硬度较高的球形钢材、陶瓷等材料的粒子，在钻井液的携带下高速冲击岩石与切削齿刮切岩石共同作用破碎岩石的过程[5]。粒子以钻井液为载体，经过PID钻头，经加速喷嘴提高粒子冲击速度进而高速冲击岩石，在岩石表面形成瞬时的巨大冲击应力。最终使岩石产生大量岩屑和裂纹，形成破碎坑，从而提高PID 钻头的破岩效率[6-7]。粒子冲击钻井技术自2002 年提出以来[8]，就成为国内外学者关注和研究的焦点。PDTI 公司经过三代粒子冲击钻井设备的研发改进，2009 年首次使用ϕ165.1 mm PID 钻头完成64 口井的现场应用[9-10]，PID 钻头如图1a 所示，并于2011 年使用新型PID 钻头完成了钻进229 h，总进尺3 490 m 的任务，现场试验表明在硬地层该技术能提速2∼4 倍[11-12]。2013 年9 月上旬，中国首次粒子冲击钻井技术现场试验在西南油气田龙岗顺利进行，在2 843.72 m 处达到1.90 m/h 的钻进速度，该试验表明，粒子冲击钻井技术较常规钻井能提速3∼4 倍[13]。目前，对粒子射流破岩机理认识尚不明确，且现有PID 钻头不能适用于所有地层[4]，因此，学者们针对上述问题进行了大量室内实验与数值仿真。在实验方面，研究人员主要借助水射流实验装置开展相关实验研究，探索了水压、粒径、作用时间及入射角度等对入侵深度和宽度的影响规律[14-19]，并结合PID 钻头流道、喷嘴类型、不同粒径和粒子浓度下对硬岩的破岩深度和破岩量进行研究[20-22]。粒子冲击破岩的穿透深度和破碎体积是评价破岩效率的重要指标，因此，也有学者开展相关研究[23]。在数值模拟方面，主要借助有限元方法开展粒子冲击对岩石的破碎机理研究，如，利用LS-DYNA 建立了三维的粒子侵彻模型，对单粒子和多粒子干涉作用下，冲击参数和围压对岩石破碎体积与侵入深度的影响进行了研究[24]。此外，也有学者应用SPE-FEM 耦合法[25]、IDFEM 软件[26]和非线性有限元方法[27]研究了粒子冲击时岩石的动态响应及其损伤演化和破坏机理、粒子冲击破岩规律和模拟磨料粒子破碎结构体过程。针对粒子注入系统、粒子分离与回收系统也展开了系列工作[28-29]，目前基本能达到使用目的。

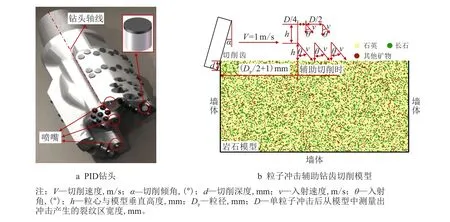
图1 PID 钻头及切削运动图Fig.1 PID bit and cutting motion diagram

上述研究虽具有一定适用性，但粒子冲击破碎岩石的尺度有限，未能从微观尺度深入剖析其作用模式与破岩机理，此外，关于粒子冲击辅助钻齿切削破碎岩石方面的研究极少。本文采用能观测岩石的裂纹扩展及岩屑形成的离散元颗粒流法，从粒径、入射角度及入射速度3 方面结合岩石切削，研究粒子冲击辅助破岩对切削齿破岩效率的影响。研究结果对优化PID 钻头、提高钻井速度及降低钻井成本有重要意义。

1 粒子冲击钻头破岩实验及模型建立

1.1 模型建立

在钻井过程中，钻头上的每个切削齿以钻头轴线为中心，以一定的角速度对井底岩石进行破碎。为方便研究，在二维的数值模拟中，将切削齿三维中的圆周运动转化为一定线速度的平面运动。本文使用颗粒流离散元法（Particle Flow Code，PFC，最早由Cundall[30]根据离散元法提出的颗粒流而开发的同名软件，该软件能直观呈现岩石的微观劣化特征）建立了无围压下粒子冲击辅助钻齿切削破岩模型，岩石模型在切削方向和切削垂直方向分别用位于两侧的无摩擦的刚性墙体和下方无摩擦的刚性墙体进行约束，如图1b 所示。

粒子冲击辅助钻齿切削破岩模型中黑砂岩数值模型大小为40 mm×20 mm，共22 435 个颗粒。粒子冲击辅助钻齿切削破岩模型中下排最左侧粒子与左墙体距离为（Dp/2+1）mm，同一排的粒子粒心距为D/2，上排最左侧粒子与下排最左侧粒子粒心距为D/4。粒子冲击产生大量微裂纹和破碎坑后，再用切削齿在V为1 m/s，切削行程为15 mm，α 为15°，d为2 mm 的情况下切削，如图1b 所示。

1.2 材料标定与验证

岩石参数标定是利用颗粒流进行破岩规律探讨的关键：通过设置材料微观参数，进行单轴压缩和巴西劈裂数值模型实验。若仿真出的宏观特性与相应现实实验结果的宏观特性接近或基本吻合，则标定结果具有一定的可靠性，可将此岩石参数用于数值模拟计算。本文采用黑砂岩作为研究对象，由70%的石英、20%的长石和10%的其他矿物组成[31]，材料模型采用平行黏结模型。考虑到实际岩石的聚团特性，利用FISH 函数随机生成不同矿物占比的黑砂岩试样，如图1b 所示。对黑砂岩进行单轴压缩和巴西劈裂实验，结果如表1 和表2所示。

表1 黑砂岩单轴压缩实验结果Tab.1 Experimental results of uniaxial compression of black_sandstone

表2 黑砂岩巴西劈裂实验结果Tab.2 Experimental results of Brazilian splitting of black_sandstone

在PFC 中建立二维实验试件进行数值模型实验，校核所选的颗粒微观材料参数。单轴压缩实验试件大小为ϕ25 mm×50 mm，巴西劈裂实验试件大小为ϕ25 mm×25 mm。最终得到黑砂岩的微观参数，结果如表3 所示。为进一步验证标定的岩石微观参数结果，对标定后的黑砂岩进行二维数值模拟切削，试件大小为ϕ40 mm×20 mm。

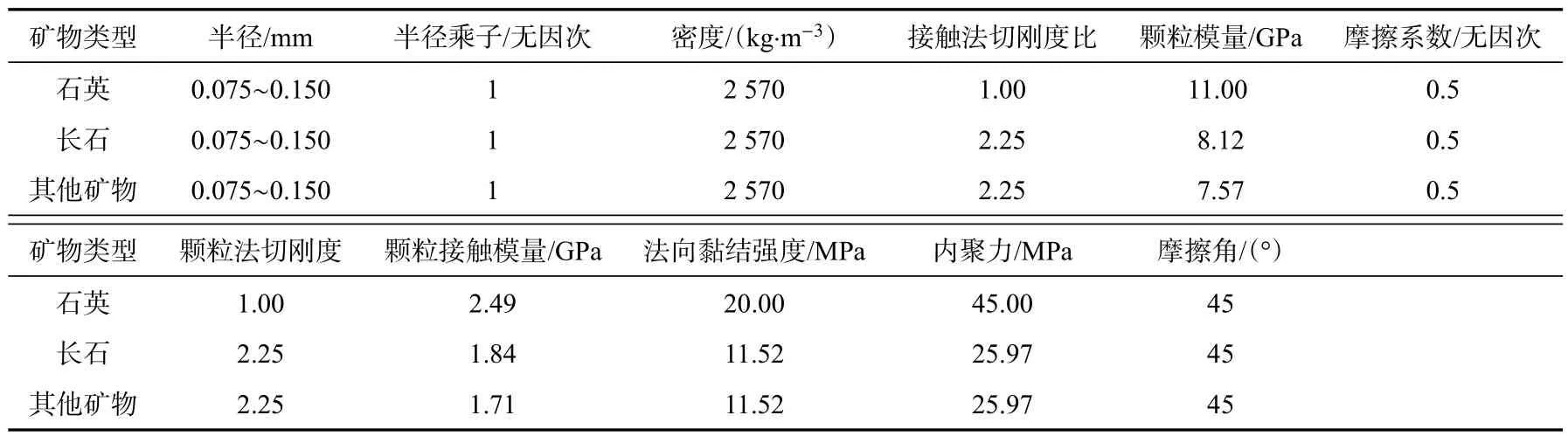
表3 黑砂岩二维离散元微观参数标定结果Tab.3 Calibration results of two-dimensional discrete element microscopic parameters of black sandstone

实验与数值模拟结果对比如图2 和图3 所示，图2a 和图3a 是二维单轴压缩和巴西劈裂数值模拟实验结果，图2b 和图3b 为黑砂岩试件实验后岩样形貌。结果表明，数值模拟结果与实验结果基本吻合。

图2 单轴压缩实验和数值模拟结果Fig.2 Results of uniaxial compression experiment and numerical simulation

图3 巴西劈裂实验和数值模拟结果Fig.3 Results of experiment and numerical simulation in Brazilian splitting

数值模拟实验中还得到试样的轴向应力（载荷）、裂纹数和轴向应变的关系曲线，如图4 所示，单轴压缩和巴西劈裂的裂纹数曲线中oa段没有裂纹产生，为压实阶段；ab段裂纹衍生，可以发现裂纹先在靠近加载墙1 和加载墙2 产生并向岩样中心发展；bc段裂纹数呈指数型增长。在c点裂纹数达到峰值，试样被压溃。综合单轴压缩和巴西劈裂的数值模拟实验，可以得到试样的弹性模量、泊松比、抗拉强度和抗压强度，将之与表1 和表2 岩石的宏观参数作比较，比较结果如表4 所示。

表4 二维数值模拟实验与实际参数对比Tab.4 Comparison of two-dimensional numerical simulation experiment and actual parameters

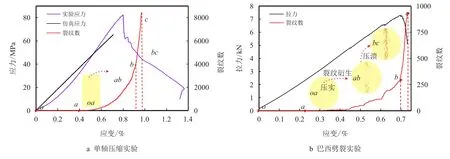
图4 实验标定曲线图Fig.4 Experimental calibration curve

表4 表明，采用平行黏结模型会导致数值模拟的抗拉强度与实验结果相差甚远，这是由接触模型的内在属性导致的（仿真结果压拉比不可能很大[32]）。数值模拟实验所得的弹性模量、泊松比及抗压强度的误差分别为1.87%、4.90%及1.21%，均小于5.00%，数值模拟实验所得宏观特性与实际基本吻合，参数标定结果具有一定的可靠性。

为增强标定结果的可靠性，建立如图1b 中所示的钻齿切削模型，V为1 m/s，切削行程为20 mm，α 为15°，d为1 mm 的黑砂岩切削实验和数值模拟切削实验。室内单齿切削实验（以下称为实验）和数值模拟实验最终得到切削齿的平均切削力，如图5 所示。取实验的平均切削力和数值模拟实验的平均切削力作对比，得出二者误差为3.12%，再次说明所建模型的合理性，标定后的模型参数见表3。

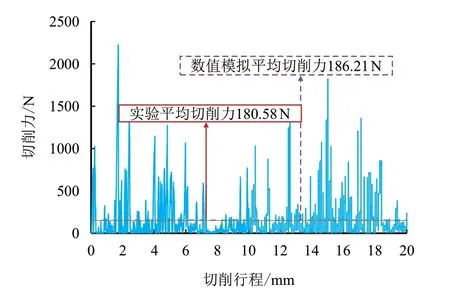
图5 切削力验证Fig.5 Cutting force verification

1.3 数值模拟可行性验证

为验证使用PFC 软件进行数值模拟的可行性，本文进行单粒子冲击破岩实验并在PFC 中建立如图6所示的单粒子冲击模型。实验装置主要包括粒子发射器、四川黑砂岩及实验记录仪器等。实验用的钢粒子粒径分别为3、4、5、6、7 及8 mm，实验黑砂岩大小为180 mm×180 mm×130 mm。实验中调节粒子发射器将钢粒子的入射速度达到50、100 及150 m/s，通过调节黑砂岩位置使钢粒子以0°、20°、40°及60°的入射角度冲击岩石，利用实验记录仪器将钢粒子冲击岩石的初速度及冲击破岩过程记录下来。

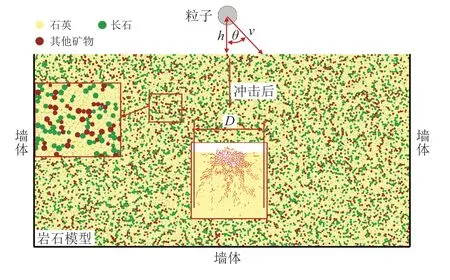
图6 单粒子冲击模型Fig.6 Single particle impact model

不同粒径的钢粒子和冲击后具破碎坑形貌的岩石如图7a 和图7b 所示。在PFC 软件中进行数值模拟时粒子的Dp、θ 和v 均与实验中一致。由于仅凭肉眼不能看到岩石内部的微观变化，在此对单粒子冲击实验和数值模拟所产生的最大破碎坑宽度L进行宏观对比，结果如图7c 所示。图中，实线和虚线分别对应实验和数值模拟的结果，a∼i 为实验后破碎坑形貌，a∼i 的颜色与数据图颜色一样对应不同入射角度。在θ 为定值时，不论是实验还是数值模拟，L都有随Dp增大而增大的趋势；当粒径一定时，L随θ增大先增大后减小。由图7c中d—f 点对应的破碎坑形貌清晰可见，当钢粒子Dp为7 mm 和8 mm 时，虽然冲击所产生的L较6 mm 粒径时产生的L小，但在这两种粒径下，钢粒子冲击后岩石破碎范围更广，破碎效果较6 mm 粒径下的好。图7c 中除去个别实验与数值模拟结果差别较大的点之外，其他实验与数值模拟结果误差均在20%之内。当钢粒子Dp和θ 分别为6 mm 和40°，v 分别为50、100 及150 m/s 时，数值模拟得到的L分别为1.2、4.2 及4.6 mm，实验得到的L分别为1.5、4.1 及4.2 mm，二者误差均在20%之内。由此认为利用PFC 软件建立的黑砂岩模型研究粒子冲击破岩具有可行性。

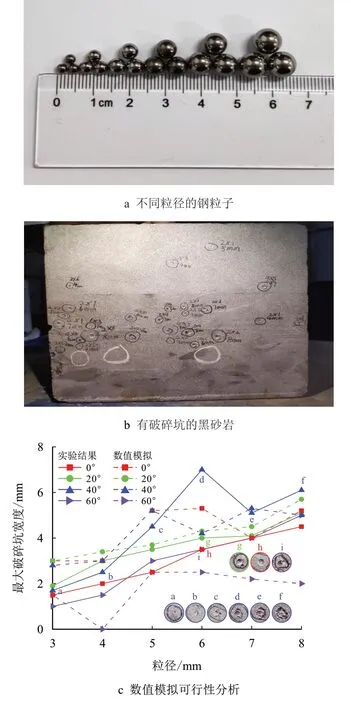
图7 单粒子冲击破岩实验与结果分析Fig.7 Experiment and result analysis of single particle impact rock breaking

2 结果分析与讨论

在离散元中作用在颗粒黏结上的应力（拉应力或剪应力）大于黏结的抗拉强度或者抗剪强度时，黏结断裂，颗粒与颗粒之间微裂纹产生，裂纹能定量地表达数值模型的损伤演化[33]，损伤不断累积最终造成模型宏观破坏。

2.1 单粒子冲击劣化岩石规律

单粒子冲击模型中粒子的粒心距左墙体20 mm、下墙体（20 mm+h）；考虑到实际钻井环境，自此选用粒径为1.0∼4.0 mm，增量为0.5 mm；入射速度在50∼300 m/s，增量为50 m/s；入射角度取0°∼60°，增量为5°，共计546 组单粒子冲击数值计算。当粒径小于等于2.0 mm 时，h为3 mm；粒径大于2 mm 时，h为6 mm。

图8a∼图8g 给出了在单粒子冲击作用下，其不同粒径、入射角度及入射速度对岩石模型产生裂纹数的情况。图8h 是2.5 mm 的粒子在距左墙体距离为2.0∼24.5 mm、增量为4.5 mm，h为6 mm，入射角度为0°∼60°时，以300 m/s 的入射速度冲击岩石所产生的裂纹数。

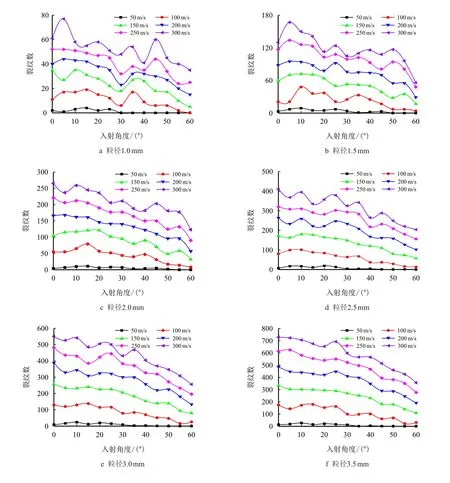
图8 单粒子及考虑岩石非均质与冲击位置对裂纹数的影响Fig.8 Single particle and the influence of rock heterogeneity and impact position on crack number

由图8 可以看出，入射角度和入射速度值不变，粒径越大，岩石模型产生的裂纹数越多。这是因为当粒子直径越大时，与岩石的接触面积越大，获得的动能越大，产生的接触应力影响范围也就越大。

当粒径小于等于2.0 mm 时，粒径、入射速度值一定，裂纹数总体上是随着入射角度的增加而减小，与之前研究不同的是随角度的变化裂纹数波动较大。当粒径大于2.0 mm 时，在同一粒径下、入射速度小于等于150 m/s 时，裂纹数随入射角度的增加而减少且波动较小，当入射速度大于150 m/s 时，裂纹数总体上也是随着入射角度的增加而减小，但随入射角度的变化裂纹数波动较大。由图8h 可见，粒子在距左墙体的距离发生变化后，其裂纹数会发生波动，该现象与单粒子入射时一致。裂纹数发生波动的原因在于本文模型考虑了岩石的非均质性，粒子与岩石作用时由于岩石矿物成分的不同导致颗粒间黏结键的断裂会产生差异。粒径小于等于1.5 mm 时，粒子入射角度从0°增加到10°时，裂纹数总体呈先增加后减小的趋势，粒径大于1.5 mm 小于等于3.0 mm 时，粒子入射角度从0°增加到10°时，裂纹数总体呈先减小后增加的趋势，粒径大于3.0 mm 时，粒子入射角度从0°增加到20°时，裂纹数总体呈逐渐减小的趋势。呈现这种裂纹数总体上随入射角度增大而减小的原因是：随入射角度的增加，粒子更趋于沿岩石表面的切向滑动，所受岩石反作用力小，入射速度在岩石纵深的分解值较小，因此，裂纹数会减少。

当粒径和入射角度值不变，裂纹数总体呈现随粒子入射速度增大而增多的规律，当入射速度小于100 m/s 时，裂纹数很少，几乎没有。当速度较小时，粒子获得的冲击动能较小，与岩石接触时产生的冲击应力未超过岩石颗粒的破坏强度，则产生裂纹数较少，破坏效果不明显。

因此，在如图6 所示的模型中，当粒径在1.0∼4.0 mm，其优选入射角度为0°∼25°，优选入射速度皆为300 m/s。

为研究多粒子冲击的粒径、入射角度和入射速度对岩石裂纹数产生的规律性是否与单粒子冲击的一致，建立多粒子冲击模型，其中，粒子的入射角度和入射速度的大小范围与单粒子冲击中的一致。下排中间粒子位置与单粒子冲击中模型一致，下排中间粒子和剩下4 颗粒子的位置关系与图1b中多粒子的一致。多粒子冲击模型中对粒径为4.0 mm 的粒子进行数值模拟计算，得出粒子入射角度、入射速度对裂纹数的影响规律如图9 所示。由图9 可知，粒径为4.0 mm 时，当入射角度一致，裂纹数随入射速度的增加而增多；当入射速度相同时，裂纹数总体随入射角度的增加而减少，当入射速度小于等于150 m/s 时，裂纹数随入射角的增加波动较小，当入射速度大于150 m/s 时，裂纹数随入射角的增加波动较大。由此可见，粒径、入射角度及入射速度在多粒子冲击中对裂纹数产生的影响规律与单粒子冲击的一致，因此，可将单粒子冲击优选出的粒径、入射角度及入射速度用于多粒子冲击和多粒子冲击辅助钻齿切削破岩中。

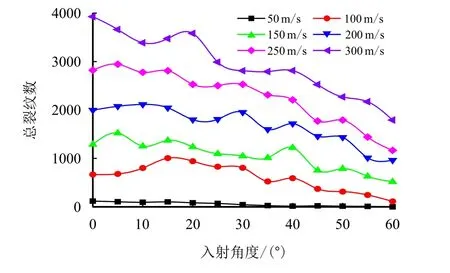
图9 多粒子冲击的裂纹数图Fig.9 Crack number of multi-particle impact

2.2 粒子冲击辅助钻齿切削破岩

破岩能耗是影响钻井效率的主要因素之一。破岩比功最早由Teale[34]于1965 年提出，从能量的角度反映了切削过程中岩石的破碎效率，其定义为破碎单位体积的岩石所耗的能量，即：WMSE=W/V0，其中：WMSE—破岩比功，MPa；W—切削齿所做的总功，J；V0—破碎岩石的体积，m3。本文中WMSE越小则说明粒子冲击破碎体积越大，粒子冲击辅助破岩效果越好。破岩过程中W可用离散元中系统能量函数追踪[35]，等于周围墙体对颗粒所做的边界能E1，即：W=E1，其中：E1—边界能，J。则WMSE可写为：WMSE=W/V0=E1/V0。

对多粒子冲击辅助切削破岩进行数值模拟，将入射速度设为300 m/s，其他参数按照单粒子优选结果设置。粒子按图1b 的方式对岩石模型进行冲击，当冲击后产生破碎坑，再用切削齿对岩石进行刮切，最后得到在有或无粒子冲击时切削齿的平均切削力FA、破岩比功及切削过程中产生的裂纹数。

表5 给出了在有或无粒子辅助破岩的情况下切削齿所受到的平均切削力，在粒子冲击辅助破岩下，切削齿受到的平均切削力远小于无粒子冲击辅助破岩下切削齿的平均切削力，且粒径越大，切削齿所受平均切削力越小，这与粒子冲击后岩石产生的破碎坑和裂纹数有关。

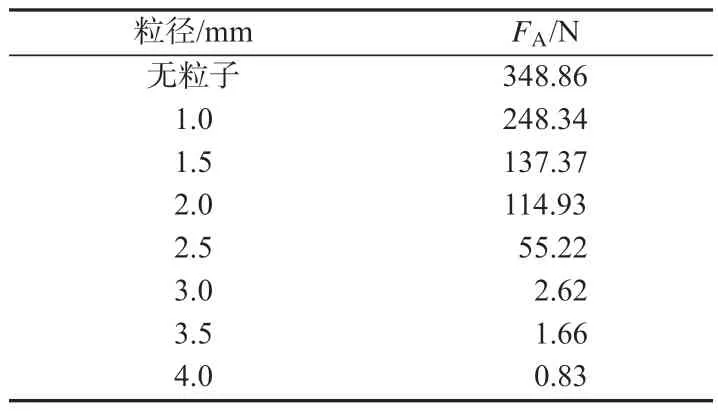
表5 切削齿所受的平均切削力FATab.5 Average cutting force FA of cutting gear

图10 为无粒子辅助钻齿破岩、多粒子冲击后岩石试样破坏形貌和粒子辅助钻齿破岩切削过程图，其中，粒子冲击岩石产生的破碎坑轮廓用蓝色线表示。不同粒径下的切削过程图的左下角为粒子冲击后岩样形貌，对应粒径为1.0∼4.0 mm 的多粒子冲击后L依次为5.05、7.76、10.68、12.35、15.86、20.51 及21.10 mm。由此可见粒径越大，产生破碎坑宽度越大，裂纹越多，辅助破岩效果越好。

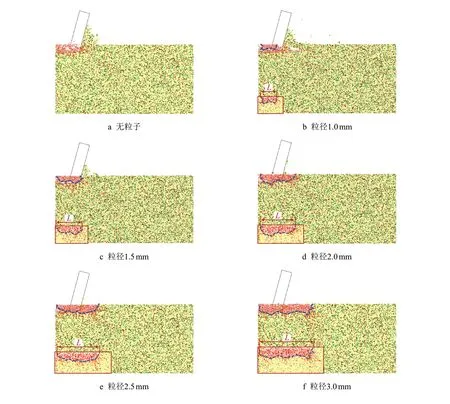
图10 切削齿在不同粒径粒子下的辅助切削过程Fig.10 The auxiliary cutting process of the cutter under different particle size

图11 为粒子冲击破碎体积和粒子冲击辅助钻齿切削破岩下切削齿的破岩比功，由破岩比功公式可得无粒子辅助破岩时切削齿的破岩比功为12.7 MPa。由此可知，粒子冲击辅助破岩的破岩比功小于无粒子冲击下的破岩比功。由图10 可知，粒径越大，粒子冲击使岩石破碎体积越大，因此，切削齿的破岩比功就越小，越有利于钻齿辅助破岩。

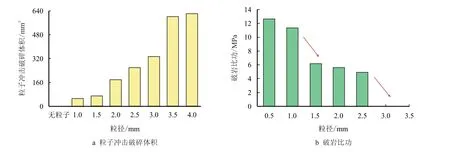
图11 粒子冲击破碎体积与破岩比功图Fig.11 Impact fragmentation volume and rock fragmentation specific work

图12 给出了有或无粒子辅助钻齿破岩情况下切削齿在切削过程中岩石产生的裂纹数。

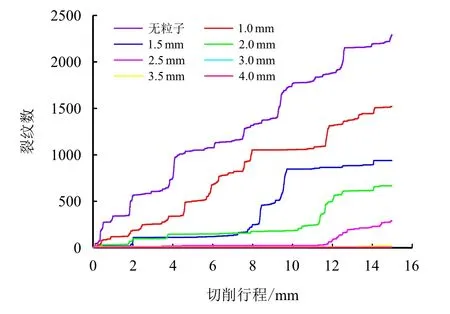
图12 切削产生的裂纹数图Fig.12 Figure of number of cracks generated by cutting

由图12 可见，无粒子辅助破岩下切削齿在切削过程中岩石产生的裂纹数远多于有粒子辅助破岩下切削齿在切削过程中岩石产生的裂纹数，当粒径越大，粒子冲击后切削齿切削过程中岩石产生的裂纹数越少。图12 中在粒子冲击辅助破岩下，切削齿切削过程中岩石产生的裂纹数有不随切削行程发生变化的现象，结合图10 冲击后岩石破碎坑形貌图分析可知，这是由于这段切削行程间的岩石在粒子冲击时被破碎，且粒径越大该情况越明显。当粒径为3.0、3.5 及4.0 mm 时，切削齿切削岩石过程中产生的裂纹数几乎为零，这是由于这3 种粒径下粒子冲击时L大于15 mm 的切削行程，切削齿在有效切削行程中较少甚至没有与岩石接触，则岩石颗粒间的黏结键断裂甚微。