基于地层取样的泥浆滤液侵入深度计算新方法
2023-11-09刘海波吴乐军张宏伟秦小飞
刘海波,吴乐军,王 猛,张宏伟,秦小飞
中海油田服务股份有限公司油田技术事业部,河北 燕郊 065201
引言
泥浆滤液侵入油气储层是一个非常复杂的过程。目前,获得泥浆滤液侵入深度主要通过实验研究和理论数值模拟两种方法。实验研究主要是对岩芯注入泥浆滤液,模拟泥浆滤液侵入地层过程,通过记录实验条件与泥浆滤液侵入量,测量岩芯电阻率变化,获得泥浆滤液侵入深度[1-3]。室内实验模拟泥浆滤液侵入地层过程中,由于实验条件不可能完全模拟地层真实条件,得到的实验结果与地层真实情况存在较大差距,且实验方法时效性差,无法用于勘探阶段快速决策[4-6]。理论数值模拟可以分为两种:一种以油水两相渗流理论、对流扩散理论为基础,利用有限元的方法对泥浆滤液侵入过程进行模拟[7-9];另一种通常以侧向测井或感应测井的工作原理,分析测井响应特征,对泥浆滤液侵入进行数值模拟[10-13]。由于理论模拟方法是间接测量,不仅存在输入参数多、影响因素复杂的缺点,而且模拟的侵入深度不确定性大、精度较低。
电缆地层泵抽取样技术(简称地层取样技术)是目前油气勘探中常用的一种动态手术式技术,可以直接从地层中获得不同纯度的流体[14-17]。基于地层取样的丰富信息,可以相对量化判断地层取样样品的污染程度[18-21],但对地层的侵入深度研究尚无先例。本文基于地层取样技术,利用泵抽过程中电导率曲线随时间动态变化的关系,确定地层流体突破时间、过渡时间及相对纯净时间;然后考虑宏观地层模型、储层物性、泵抽参数等因素,建立侵入深度体积模型,从而定量计算泥浆滤液的侵入深度,为精确地层评价、射孔参数优化设计以及压裂施工设计等提供指导性建议。
1 地层取样过程划分
地层取样的目的是获取储层中流体样品,而要判断是否抽取到真实的流体样品则要依靠多种井下监测技术。常规技术主要是通过监测井下流体的密度、黏度、电导率或电阻率等来实现。国内通过建立自主的专利技术,包括电、光、声和核磁共振等多种方法已经实现井下流体的有效识别[16,22]。应用表明,电导率较密度值监测具有变化范围大、灵敏度高的优点,因此,本文重点讨论地层取样过程中电导率曲线在流体识别方面的应用,密度曲线作为辅助参考。由于水基泥浆在水层取样或者油基泥浆在油层取样,泥浆滤液和地层原状流体混溶,取样流体为单相流,电导率显示没有明显跳动,本文不做讨论;本文重点讨论常见的水基泥浆在油层或者油基泥浆在水层进行取样,泥浆滤液和地层原状流体不混溶,取样流体为两相流,电导率有明显跳动的情况。
泥浆滤液侵入储层一般分为冲洗带、过渡带和原状地层3 个部分,通常认为,物性较好的常规储层侵入带相对较小,物性较差的超低渗储层侵入带相对较大,但很难用量化数据表征[23-24]。地层取样过程实际上为原状地层流体驱替泥浆滤液进入仪器探针吸口的过程。取样过程中,电导率信息是井下流体流过测量段管线记录的视电导率值,以曲线形式动态变化,与管线中流动的流体相态和体积有关[16]。根据地层取样过程中实时电导率曲线特征,可判断进入仪器探针吸口并监测的流体是冲洗带、过渡带还是原状地层流体。图1 为水基泥浆在油层取样时,基于泵抽时间与电导率曲线的泵抽过程划分示意图。由图1 可见,整个取样泵抽过程可划分为以下4 个阶段。
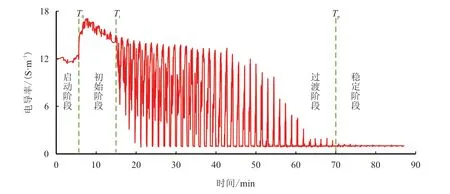
图1 基于泵抽时间与电导率曲线的泵抽过程划分示意图Fig.1 Schematic diagram of pumping process division based on pumping time and conductivity curve
1)启动阶段。管线中主要为井筒中的泥浆,监测的视电导率为泥浆的电导率。因为泥浆中存在固相物质,所以电导率比侵入地层中的泥浆滤液小。
2)初始阶段。管线中流体为来自地层冲洗带中的单相泥浆滤液,监测的视电导率显示为短暂且小幅高位波动的曲线特征,视电导率的值与泥浆滤液矿化度和地层温度有关。
3)过渡阶段。经过一定时间泵抽,当有地层流体突破后,管线中将出现来自地层过渡带中的地层流体和泥浆滤液的混合流体,即两相的段塞流,监测的视电导率曲线呈现上下剧烈跳动特征,最大值为泥浆滤液的电导率值,最小值为地层流体的电导率值。
4)稳定阶段。管线中流体逐步转变为稳定的来自原状地层中的单相地层流体,监测的视电导率曲线显示为近水平特征。海上油基泥浆在水层进行取样情况相对较少,其原理与上述相同。
上述4 个阶段中,有3 个关键时间点:泥浆滤液入管时间T0、地层流体与泥浆滤液的混合液突破时间Tt及地层流体稳定时间Tp,其中,第3 个阶段(过渡阶段)从Tt到Tp通常持续时间较长,主要受侵入深度、储层物性以及泵抽时效等控制。根据地层取样过程中地层流体突破时间Tt和稳定时间Tp,结合宏观地层模型、泵抽参数以及地层物性等,可建立侵入深度体积模型,从而确定泥浆滤液在冲洗带和过渡带距井壁的距离,即泥浆滤液的侵入深度。
2 侵入深度体积模型的建立
在地层泵抽取样过程中,地层流体一般会出现两种流动形式:球形流和柱形流(径向流)[25-27]。球形流动存在的条件是储层均质,上下界面是封闭界面,井壁也是封闭界面。仪器吸口坐封地层后,地层中的流体从吸口的四面八方流入(忽略井筒的影响)。球形流动在双对数压力-时间曲线中的导数曲线表现为一条斜率为 -0.5的直线。柱形流动存在的条件是储集层的厚度很薄,它的厚度与仪器吸口直径相当,或者储集层中有泥岩层,把流向仪器吸口的流线限制为径向流动,或者储集层是垂向渗透率等于零的储集层,这时在垂直方向上没有流动,微细水平层理结构的粒间空隙储集层容易有这样的情况。地层中流体作径向流动时,等压线是以仪器吸口为中心的圆圈(忽略井筒的影响),径向流动在双对数曲线中导数曲线表现为水平线。
2.1 模型建立
实际应用过程中,由于存在地层各向异性,流体在地层中流动形式一般为不是单纯的球形流或径向流,而是球形流和径向流相结合的椭圆形流,如图2 所示。假设在水平均质地层且储层厚度较厚的情况下进行地层泵抽取样,对此,可以建立如下物理模型。
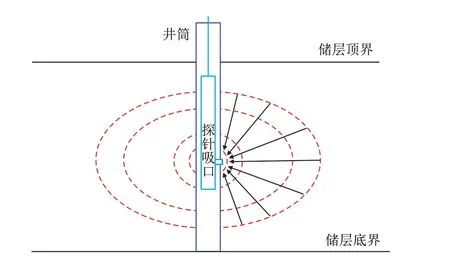
图2 地层中流体流动椭圆形流形示意图Fig.2 Schematic diagram of the elliptical manifold of fluid flow in the formation
1)地层为无限大等厚油藏,均质且水平各向同性。
2)不可压缩液体在地层中作球形稳定渗流,忽略重力和毛细管力。
地层泵抽取样过程中,根据质量守恒,泵抽流体的体积与地层中流出的体积相等。泵抽流体波及范围受井筒影响,体积模型是一个椭球体被井筒圆柱体切割后的剩余体积。椭球体的形状受水平渗透率和垂直渗透率影响,建立模型,泵抽流体体积模型
式中:P—已知设定的泵抽速度,mL/min;
T—泵抽时间,min;
β—模型形状因子,无因次;
ϕ—地层有效孔隙度,%;
KH—地层水平渗透率,mD;
KV—地层垂直渗透率,mD;
X—泵抽流体在地层中波及深度,cm。
式(1)中的模型形状因子,是泵抽流体在地层中波及深度和井筒半径的关系函数。当开始泵抽,即泵抽流体在地层中波及深度X→0 时,忽略井筒的曲率对体积模型的影响,体积模型是半个椭球体的体积,β=0.50;当X与井筒直径相等时,体积模型是椭球体被井筒圆柱体切割后的剩余体积,β=0.75;当X→∞时,忽略井筒的影响,体积模型是一个椭球体的体积,β=1.00。β 和侵入深度与井径之比的关系曲线如图3 所示,基于此,可得到模型形状因子的表达式,如式(2)所示。
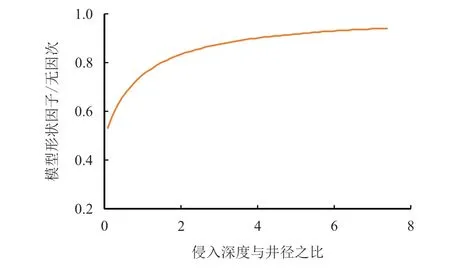
图3 模型形状因子和侵入深度与井径之比的关系Fig.3 The relationship between β and the ratio of invasion depth and well diameter
式中:rc—井筒半径,cm。
式(1)和式(2)联合,可确定泵抽流体在地层中波及深度,该深度即为泥浆滤液的侵入深度。
2.2 影响因素分析
地层泵抽取样过程,并不是简单的泥浆滤液侵入地层的反转过程。在泵抽取样过程中,地层流体要驱替泥浆滤液,同时,流体的流形也在不断变化,最终进入流管地层流体的纯度将受多种因素影响。其中,地层岩性物性、流体物性、仪器参数、井筒尺寸和储层污染程度是关键因素。地层岩性物性包括岩石的润湿性、有效孔隙度、饱和度及水平与垂直渗透率比值等;流体物性包括流体的黏度与压缩性等;仪器参数包括泵抽设定的泵速、泵抽时间和探针吸口面积等;井筒尺寸参数包括井筒半径和井况等参数。
2.2.1 地层岩性物性的影响
对于低孔渗储层的两相流,如果岩石孔隙结构存在优势通道(地层各向渗透率存在差异),驱替过程可能存在指进现象,因此,模型计算的泥浆滤液侵入深度结果偏小。而对于中—高孔渗储层,由于受毛细管作用的扩散效应影响较小,一般不会发生指进现象,因此,模型计算结果是可靠的。在体积模型中,地层有效孔隙度,一般通过核磁测井获得;地层含水饱和度及井筒尺寸等参数可从常规测井资料获得;水平渗透率与垂直渗透率比值可通过地层测试双探针测压解释获得。这些参数的精度对模型计算结果有一定影响。
2.2.2 流体物性的影响
如果储层是稠油、气或凝析气,泥浆滤液侵入时,可能发生指进现象,而泵抽取样,地层流体驱替泥浆滤液的过程变得更加复杂,模型计算的泥浆滤液侵入深度结果误差大。针对常规地层流体,泥浆滤液与地层流体的黏度比大于0.1 时,一般认为两相流体的驱替前缘是稳定的,不存在指进现象,模型计算结果是可靠的。
由于液体具有压缩性,随着压力降低,体积要发生膨胀,同时释放弹性能量,出现弹性力。岩石的压缩性对渗流过程有两方面的影响:一方面,压力变化会引起孔隙大小发生变化,表现为孔隙度是随压力变化的状态函数;另一方面,由于孔隙大小发生变化引起渗透率的变化。由于岩石的压缩性,当压力变化时,岩石的固体骨架体积会压缩或者膨胀,这同时会使岩石孔隙体积发生变化。因而可以把岩石的压缩性看成孔隙度随压力变化。泵抽取样过程控制好压差,使压差保持在相对较小并稳定的范围内,有利于取样的成功和模型的计算。
2.2.3 仪器参数的影响
两相流体在地层中的流动速度对模型的计算有一定的影响。在取样过程中,泵速越大,产生的压降越大。近探头地层中的流体流速最大,地层深处流体的流速相对较低。地层中流体的流速与泵速和探针吸口的尺寸有关,低泵速、大面积探针吸口更有利于模型的计算,特别是低孔渗储层。地层和井下仪器内的测试室需要有管线和压力计来连接,这些附加的空间会存储流体,这个体积的大小对模型计算精度有影响,即管线存储效应或管线存储系数的影响。
2.2.4 储层污染程度的影响
由于钻井泥浆中的悬浮颗粒渗入地层堵塞孔隙通道,在井壁上形成泥饼,导致地层流体流入仪器时,会在井筒附近产生一个压力降,集中在井筒周围形成一个很薄的柱形“表皮区”,把这个现象称为表皮效应。由于表皮效应的存在,使实际的压力分布不同于理想的压力分布。表皮效应主要是影响测压的解释,对于地层泵抽取样,由于泵抽时间长,井壁的表皮效应影响较小。但对于低孔渗储层,由于泥浆污染严重,侵入比较深,泵抽过程中地层流体的流形可能会发生变化,影响模型中的形状因子,导致模型计算误差增大。
3 应用实例
3.1 实例1
海上某油田A 井是一口预探井,目的是落实该凹陷新近系明化镇组的含油气性,实现该构造油气勘探突破。图4 是该井1 475.0∼1 485.0 m 层段的测井响应解释成果图,该井段砂体特征明显,物性较好,电阻率在20 Ω·m 左右。
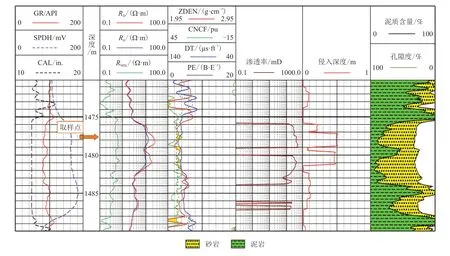
图4 海上某油田A 井测井响应解释成果图Fig.4 Log response interpretation results of Well A in an offshore oilfield
为了确定储层流体性质,在A 井1 477.5 m 处进行电缆地层测试取样,记录泵抽时间与电导率值曲线如图5 所示,泵抽的4 个阶段非常清晰,泵抽初始时间为4.3 min,原油突破时间为15 min,原油稳定时间为118 min。仪器使用标准探针的吸口面积为5 cm2,设定的泵抽速度为320 mL/min。常规测井资料获得该井筒半径为15.56 cm,地层有效孔隙度为21.8%,地层水平渗透率与垂直渗透率比值为10。用本文方法通过迭代计算分别获得泥浆滤液侵入冲洗带深度为0.27 m,泥浆滤液侵入过渡带深度为0.53 m。
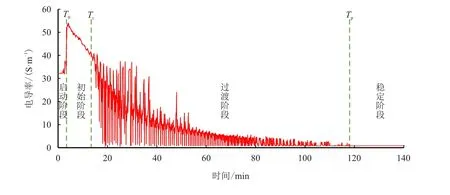
图5 A 井1 477.5 m 处泵抽时间与电导率曲线图Fig.5 Curves of pumping time and conductivity at 1 477.5 m in Well A
传统方法根据双侧向电阻率反演获得该点的侵入过渡带深度为0.49 m,电阻率测井作业在电缆地层测试测井作业之前,电阻率反演方法计算的侵入深度较本文方法计算结果偏小,符合实际情况。该方法理论依据充分,适用性强,计算速度快,但基于数值模拟,计算结果需要实验标定,计算结果可靠性差。
采用油藏数值模拟方法,在相同的条件下模拟计算侵入深度。假设油藏恒温,流体可轻微压缩,用黑油模型中的水相代表泥浆滤液,地层无限大,外边界条件为等压条件。
以井筒为中心建立三维径向网格,探针附近的网格较稠密,远离探针的网格较稀疏。用圆形探针和三维径向坐标,划分的网格具有对称性,因此,只需包含1/2 的探针及地层进行模拟计算即可。输入参数如表1 所示(其中,1 psi=6.895 kPa),侵入深度模拟结果如图6 所示。

表1 A 井1 477.5 m 处数值模拟输入参数Tab.1 Numerical simulation input parameters at 1 477.5 m in Well A
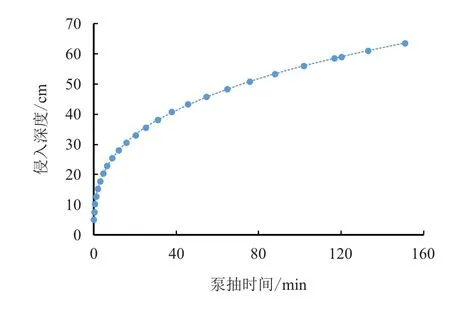
图6 A 井1 477.5 m 处侵入深度数值模拟结果Fig.6 Numerical simulation results of invasion depth at 1 477.5 m in Well A
由图6 可见,原油突破时间为15 mim 时,插值法计算泥浆滤液侵入冲洗带深度为0.30 m;原油稳定时间为118 min 时,插值法计算泥浆滤液侵入过渡带深度为0.59 m。该方法计算结果可靠性强,但需要输入参数多,计算过程复杂,时效性差。
3.2 实例2
海上某油田B 井是一口预探井,目的是落实该凹陷流沙港组三段的含油气性,实现该构造油气勘探突破。
该井2 820.0∼2 840.0 井段砂体特征明显,为低孔低渗储层,电阻率约4 Ω·m,流体性质不明,为此,在2 836.5 m 处进行电缆地层测试取样,记录泵抽时间与电导率值曲线如图7 所示,仪器使用标准探针的吸口面积为5 cm2,设定的泵抽速度为220 mL/min,对应该井段的测井曲线见图8。常规测井资料获得该井筒半径为15.56 cm,地层有效孔隙度为15.2%,地层水平渗透率与垂直渗透率比值为10。用本文方法通过迭代计算分别获得泥浆滤液侵入冲洗带深度为0.47 m,泥浆滤液侵入过渡带深度为0.80 m。
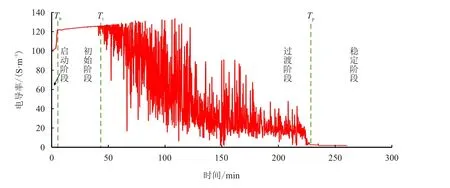
图7 B 井2 836.5 m 处泵抽时间与电导率曲线图Fig.7 Pumping time and conductivity curve at 2 836.5 m in Well B
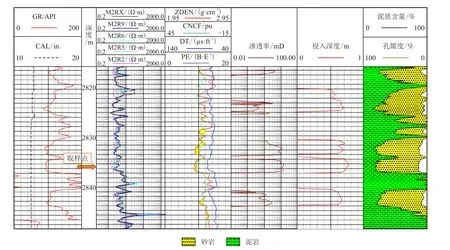
图8 海上某油田B 井测井响应解释成果图Fig.8 Log response interpretation results of Well B in an offshore oilfield
同实例1 类似,传统方法根据双侧向电阻率反 演获得该点的侵入过渡带深度为0.75 m。采用油藏数值模拟软件在相同的条件下进行数值模拟计算侵入深度,输入参数如表2 所示,输出泵抽时间与泥浆滤液侵入深度的关系如图9 所示,即原油突破时间为42.5 min 时,插值法计算泥浆滤液侵入冲洗带深度为0.44 m;原油稳定时间为228.0 min 时,插值法计算泥浆滤液侵入过渡带深度为0.76 m。
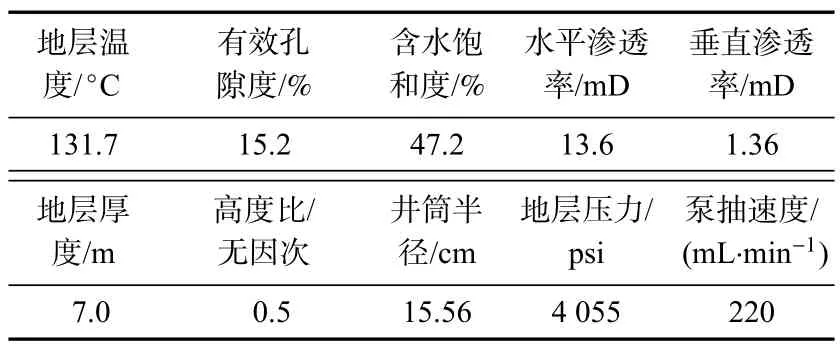
表2 B 井2 836.5 m 处数值模拟输入参数Tab.2 Numerical simulation input parameters at 2 836.5 m in Well B
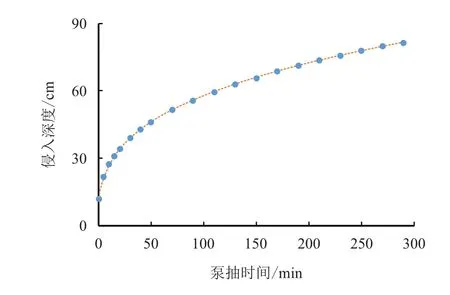
图9 B 井2 836.5 m 侵入深度关系数值模拟结果Fig.9 Numerical simulation results of invasion depth at 2 836.5 m in Well B
不难看出,B 井目标储层为低孔低渗储层,侵入深度相对较大,应是导致其电阻率下降明显的主要原因。取样结果表明该储层流体性质为油层。本文方法在海上数十口探井进行了应用验证,计算结果与油藏数值模拟软件计算结果一致性好,说明本方法计算结果的可靠性强,方法简便,时效性更高。
4 结论
1)基于地层泵抽取样技术,利用泵抽取样过程中时间和电导率曲线的动态关系,把泵抽过程划分为4 个阶段,即启动阶段、初始阶段、过渡阶段和稳定阶段,据此可实时清晰了解泵抽流体的性质和来源。
2)基于宏观地层模型、储层物性、泵抽时间与速度等因素,建立了泥浆滤液侵入深度的体积模型,提出了定量计算泥浆滤液侵入深度的新方法,计算结果较传统的数值模拟方法,时效性更高,可靠性更强。
3)深入分析了地层岩性物性、流体物性、仪器参数和储层污染程度等关键因素对体积模型计算结果的影响,通过海上数十口探井的应用验证,取得了很好的效果,为现场作业决策提供重要依据。
