坠物撞击海底管道损伤的BP神经网络预测模型
2023-11-09张春会赵文豪田英辉牛习现佘虹宇齐晓亮
张春会,赵文豪,田英辉,牛习现,王 乐,黄 鑫,佘虹宇,齐晓亮
(1.河北科技大学建筑工程学院,河北石家庄 050018;2.河北省岩土与结构体系防灾减灾技术创新中心,河北石家庄 050018; 3.墨尔本大学基础设施工程系,维多利亚墨尔本 3010;4.河北青年管理干部学院信息系,河北石家庄 050031;5.天津大学水利工程仿真与安全国家重点实验室,天津 300354;6.中海油能源发展股份有限公司采油服务分公司,天津 300451)
海底管道是海洋油气输送的生命线,在服役期内除遭受波流和温度荷载作用外,还经常遭受拖网渔具、抛锚、集装箱与其他坠落物等偶然荷载的撞击,威胁海底管道安全[1-5]。已有统计数据结果表明,47%的海底管道故障是由这些偶然荷载撞击引起的[6]。在坠物等偶然荷载撞击下,海底管道的损伤预测是海底管道安全防护技术研究的基础。目前,国内外对于坠物撞击下海底管道损伤预测开展了很多研究[7-21]。总体来看,目前国内外主要采用DNV RP-F107规范[7]公式预测海底管道损伤,但该公式假定海床为刚性,这与实际海底海床条件并不符。TIAN等[16]采用数值模拟方法分析了海床土力学特性对海底管道损伤的影响,给出了类似于DNV规范的海底管道损伤计算经验公式。这些计算公式在计算管道损伤时都需要先确定坠物撞击下海底管道的吸收能,然而海底管道吸收能受海床土力学特性、管道特性及坠物特性等诸多因素的影响,目前尚无有效的方法对其进行估算,针对具体工程只能通过数值模拟确定相应的管道吸收能,这给海底管道损伤预测带来了极大不便。
BP神经网络是一种典型的前馈型网络,适合在大量数据基础上建立复杂的非线性映射[22],为直接通过坠物、管道和海床土特性预测受撞击海底管道损伤提供了新思路。本文在ABAQUS下建立坠物撞击海底管道的数值模型,开展大量数值模拟,分析坠物撞击能量、管道直径与壁厚、钢材等级、内压和海床土力学特性对管道损伤的影响,将模拟结果作为训练样本建立管道损伤BP神经网络预测模型,为海底管道损伤预测提供一种新的方法。
1 坠物撞击海底管道的数值模型
本文在有限元软件ABAQUS中建立坠物撞击下海底管道与海床土相互作用的动力数值模型。
1.1 数值模型建立
海底管道为X60型钢,管道直径D为1 m,质量密度为7 850 kg/m3,杨氏模量为2×1011Pa,泊松比为0.3,管道为Mises材料,屈服强度为450 MPa,采用S4R壳体单元进行模拟。海床为饱和黏土,土体有效质量密度为600 kg/m3,坠物撞击时间短,土体为不排水状态,Tresca材料,内摩擦角与剪胀角均为0,泊松比为0.49,海床土不排水抗剪强度Su=10 kPa,弹性模量为500Su,土体采用C3D8R实体单元模拟。已有研究结果表明[16],在撞击能量相同的条件下球形坠物造成的管道损伤最大。本文将坠物简化为球形进行计算。球形坠物直径为1 m,质量为1.9 t,将球形坠物视为刚体,采用C3D8R实体单元模拟,坠物撞击点为管道中央。根据球形坠物撞击海底管道的对称性,沿球形坠物中心和撞击点,取半模型进行数值分析,如图1所示,其中xoz面为对称面,y轴方向为沿管道轴向,z轴方向为海床高度方向。

图1 坠物撞击管道有限元模型图Fig.1 Finite element model of subsea pipe striked by falling object
海床长宽高分别为16D,16D和10D,海底管道平铺于海床上,长度为16D。坠物受到海水阻力,下落一定深度后速度不变[7],数值模型中半球形坠物从管道上方匀速竖直下落。海底管道与饱和黏土海床之间摩擦系数为0.3,海床土底部边界固定,前后左右4个表面边界只允许垂直移动。在管-土接触长宽高方向1D范围内网格加密。经过试算,加密区域网格尺寸为D/40,建立的球形坠物动力撞击海底管道数值模型如图1所示。
1.2 损伤定义
管道损伤示意图见图2。坠落物撞击海底管道,Q1点为撞击前管道的上部中心点,即球形落物撞击管道的撞击点,P点为撞击前管道下底点,Q1与P之间的距离为管道直径D,管道上部中心点受到竖向撞击,Q1点产生竖向变形,向下移动至Q2点,Q1和Q2之间的距离即为撞击引起的竖向凹陷深度δ,本文中管道损伤定义为
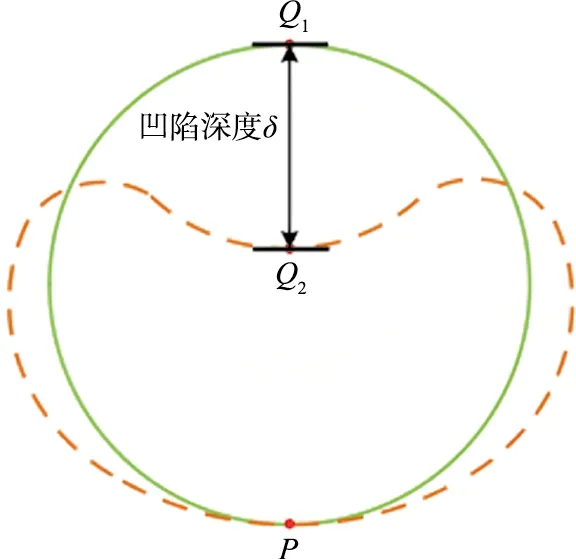
图2 管道损伤示意图Fig.2 Diagram of pipe damage
(1)
1.3 模型验证
利用本文数值模型,模拟PINHEIRO等[23]开展的刚性床上支撑管道加载实验,同时将本文数值模拟结果与DNV RP-F107[7]的规范公式计算结果进行对比,验证本文数值模型的正确性。
1.3.1 刚性床上管道承受横向荷载实验
文献[23]利用半球形压头对支撑在刚性底座上的管道(D=73 mm,t=3.05 mm)进行静态横向加载实验,在距离中心点17 mm和25 mm处分别布设4个环向和轴向应变片,编号为SG1,SG2,SG3和SG4,如图3所示,测试压头加载过程中4个测点的应变值。利用本文数值模型模拟实验过程,在数值模拟中,压头和海床均为刚体,靠近管道-压头相互作用区域使用细小网格(0.05D),其余区域使用0.2D的单元尺寸,数值模型如图4所示。

图3 实验模型图Fig.3 Experimental model diagram
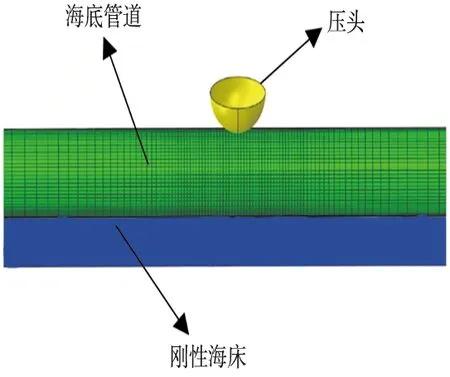
图4 数值模型图Fig.4 Numerical model diagram
数值结果和实验结果对比见图5,其中横轴为应变,纵轴为压头位移。SG1和SG3沿轴向和环向测得的应变负值表示拉伸,正值表示收缩。由图5可见,在加载初始阶段,压头加载应变增长较缓;压头位移超过约1.7 mm后,应变增长速率变快。这是由于压头位移超过约1.7 mm后,管道初始圆形横截面发生显著变形,管道变得更加柔韧,呈现出更快的应变增长速率。由图5可知,数值模拟结果与实验结果基本吻合,表明本文数值模型可靠。
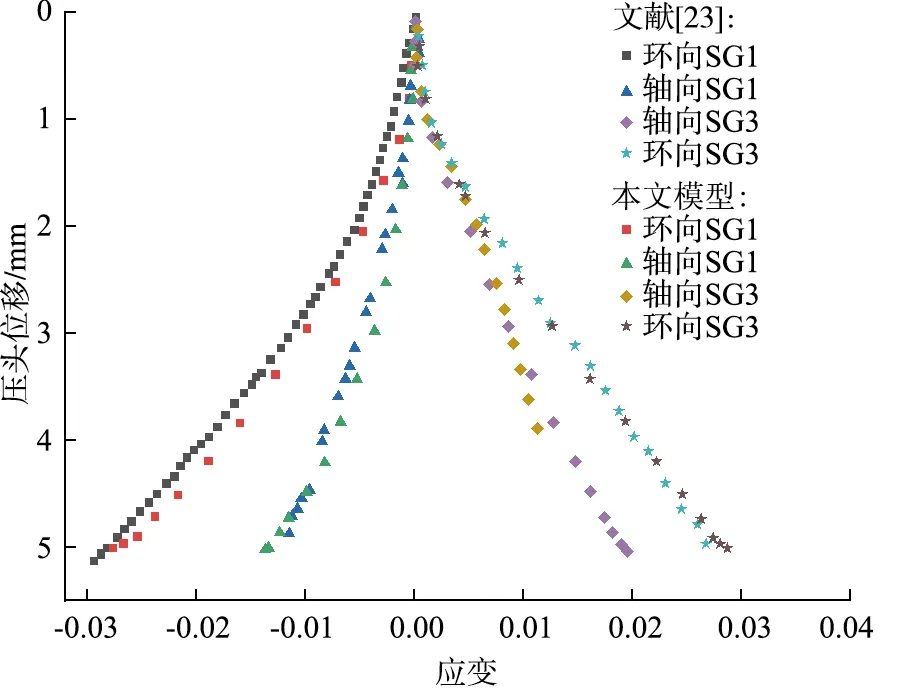
图5 本文数值模拟结果与实验结果对比Fig.5 Comparison of numerical simulation results with experimental results in this paper
1.3.2 数值模型与DNV规范对比验证
DNV RP-F107规范[7]给出了刚性海床上海底管道受楔形坠物撞击的凹痕损伤计算公式为
(2)
式中:E为管道吸收能量;σy为管道屈服应力;δ为管道凹陷深度;t为管道壁厚。
将本文数值模型中的海床改为刚性海床,坠物形状修改为楔形,将楔形坠物视为刚体,楔形坠物采用C3D8R实体单元进行模拟,撞击点为管道中央;海底管道为X60型钢,管道直径为1 m,质量密度为7 850 kg/m3,屈服强度为450 MPa,杨氏模量为2×1011Pa,泊松比为0.3,管道为Mises材料,采用S4R壳体单元进行模拟,取半模型进行数值分析。管道与海床之间光滑无摩擦,楔形坠物位于管道上方0.1 m处,海床刚性面的边界条件被完全限制,管道的远端被完全固定,管道的近端约束法向移动,楔形坠物只沿竖向运动,如图6所示。算例中楔形坠物撞击能量从3.5 kJ增加到197 kJ,数值计算获得的管道损伤与DNV RP-F107规范计算结果对比如图7所示。由图7可知,数值模拟结果与DNV规范计算结果相差不超过5%,表明本文数值模型计算可靠。

图6 数值模拟验证模型Fig.6 Numerical simulation to validate the model

图7 本文数值结果与DNV公式结果对比Fig.7 Comparison between the numerical results in this paper and the results of the DNV formula
1.4 计算方案
坠物撞击能量、管道直径、壁厚、钢材等级及内压、饱和黏土海床强度及模量是海底管道损伤的主要影响因素。为建立坠物撞击下海底管道损伤预测的神经网络模型,使用本文数值模型对饱和黏土海床上海底管道坠物撞击开展数值模拟分析。改变坠物速度,控制坠物能量在42~198 kJ范围内,坠物能量覆盖了98%的能量带[7]。依据API Spec 5L[24]管线规范,常用的海底管道实际管径范围通常为0.5~1 m,工程中管道壁厚通常为17~25 mm,钢材等级范围X52~X80。本文分别选取海底管道直径为0.70,0.75,0.80,0.85和0.90 m,海底管道壁厚分别为19,20,21,22,和23 mm,管道钢材等级选取X52,X56,X60,X65和X70。管道输送油气资源时,内部通常处于高压状态,常见压力一般在10 MPa左右,最高不超过70 MPa[25-26]。本文分别取0(输油管道关闭)和3,6,9,12 MPa共5种管道内压值,常见海洋饱和黏土的不排水抗剪强度Su在10~50 kPa之间[27-29],饱和黏土模量为(200~1 000)Su。已有研究[16]表明,饱和黏土弹性模量对海底管道损伤影响微小,本文仅考虑不排水抗剪强度的影响,不排水抗剪强度取Su=10,20,30,40,50 kPa,饱和黏土的弹性模量取500Su。计算方案中的影响因素涵盖了绝大多数实际工程中的饱和黏土海床海底管道工作条件。本文制定了105组算例,分别研究管道直径、壁厚、钢材等级、管道内压以及海床不排水抗剪强度Su对海底管道损伤的影响,计算方案如表1所示。

表1 坠物撞击海底管道计算方案Tab.1 Falling object impact calculation program for submarine pipelines
2 计算结果及分析
2.1 管道特性参数的影响
按照计算方案1—方案25开展计算,获得不同管径与坠物撞击能量下海底管道损伤结果如图8所示。从图8可见,管道直径为0.7 m时,坠物能量42.5 kJ时引起的管道损伤为5.01%,坠物能量197.5 kJ时引起的管道损伤为17.67%。相同管道直径下,随着坠物能量的增加,管道损伤增大。从图8还可知,坠物能量为170 kJ时,管道直径0.70,0.75,0.80,0.85,0.90 m引起的海底管道损伤依次为16.01%,15.36%,15.00%,14.70%和14.36%。这表明在相同坠物能量下,随着管道直径的增加,管道损伤减小。这是由于管道直径增加,坠物和管道相接触作用面的曲率减小,冲击面积增大,对管道的撞击作用减小,相应的管道损伤也减小。

图8 海底管道直径与损伤关系Fig.8 Relationship between submarine pipeline diameter and damage
根据计算方案21—方案45,得到不同壁厚与坠物撞击能量下海底管道损伤结果如图9所示。由图9可见,管道壁厚为19 mm时,坠物能量42.5 kJ引起的管道损伤为6.66%,坠物能量为197.5 kJ时对管道引起的损伤为18.04%,相同管道壁厚下,坠物能量增加,管道损伤增大。由图9还可以看出,坠物能量为170.0 kJ、管道壁厚分别为19,20,21,22,23 mm时,海底管道的损伤依次为16.52%,16.12%,15.24%,14.52%和14.07%,表明在相同坠物能量下,管道壁厚增加,管道损伤减小。这是由于管道壁厚增加会提升管道的刚度,管道抵抗冲击荷载作用下塑性变形的能力也相应增加,从而使管道损伤相应减小。

图9 海底管道壁厚与损伤关系Fig.9 Relationship between wall thickness and damage in submarine pipelines
依照计算方案21—方案25、方案46—方案65,获得了管道不同钢材等级与撞击能量作用下海底管道损伤结果,如图10所示。文中管道钢材等级X52,X56,X60,X65和X70分别代表管道屈服强度为370,400,450,480,和520 MPa。由图10可知,管道钢材等级为X52时,坠物能量为42.5 kJ所引起的管道损伤为6.05%;坠物能量为197.5 kJ时,对管道引起的损伤为17.18%。相同管道钢材等级下,坠物能量增加,管道损伤越大。由图10还可知,坠物能量为170 kJ时,管道钢材等级分别为X52,X56,X60,X65和X70所引起的管道损伤依次为15.73%,15.12%,14.37%,13.98%和13.43%,这表明相同坠物能量下,管道钢材等级越高,管道损伤越小。这是由于管道钢材等级提高会提升管道强度,与增加管道壁厚情形类似,管道在冲击荷载作用下抵抗塑性变形的能力增加,从而使管道损伤减小。

图10 海底管道钢材等级与损伤关系Fig.10 Subsea pipeline steel grade and damage relationship
参照计算方案21—方案25和方案66—方案85,获得了不同管道内压值与坠物撞击能量下海底管道损伤情况,如图11所示。从图11可见,管道内压为0 MPa时,坠物能量42.5 kJ所引起管道损伤为4.51%,坠物能量197.5 kJ时对管道引起的损伤为15.46%,由此可见,在相同管道内压情况下,坠物能量增大,管道损伤呈负指数函数增长且减小速率趋缓。从图11还可知,坠物能量为170.0 kJ时,管道内压为0,3,6,9和12 MPa所引起的管道损伤依次为14.37%,10.77%,8.66%,6.23%和4.20%,表明在相同坠物能量下,管道内压增加,管道损伤减小。这是由于管道内压增大,有助于提高管道抵抗外界撞击的能力,减小管道损伤。

图11 海底管道内压与损伤关系Fig.11 Relationship between internal pressure and damage in submarine pipelines
2.2 海床土不排水抗剪强度的影响
土体的不排水抗剪强度Su是反映土体特性的重要力学指标,也决定了土体强度及极限承载能力。在冲击过程中,不排水抗剪强度的大小会在海底管道受坠物撞击时影响接触土体引起破坏及破坏的程度,并且在坠物撞击海底管道这一冲击过程中,土体的不排水抗剪强度Su增大,海床土吸收能减小,从而影响海底管道的损伤程度。依照计算方案21—方案25和方案86—方案105,得到如图12所示的管道损伤与不排水抗剪强度关系图。由图12可以看出,不排水抗剪强度Su=10 kPa时,坠物能量42.5 kJ所引起的管道损伤为4.51%,坠物能量197.5 kJ时对管道引起的损伤为15.46%,表明在相同不排水抗剪强度下,坠物能量增加,管道损伤增加。图13分析了坠物能量为42.5 kJ时,不排水抗剪强度与管道吸收能量及损伤关系图。不排水抗剪强度Su=10,20,30,40,50 kPa,所产生的管道损伤依次为4.51%,4.96%,5.22%,5.30%和5.37%,表明相同坠物能量时,土体不排水抗剪强度增加,管道损伤增大。这是由于海床土强度增加,土体变形和塑性区减小,土体吸收能量减小,管道吸收的能量增大,管道损伤增大。

图12 海床土不排水抗剪强度与损伤关系Fig.12 Relationship between undrained shear strength and damage in seabed soils

图13 海床土不排水抗剪强度与能量及损伤关系Fig.13 Undrained shear strength of seabed soils in relation to energy and damagea
3 海底管道损伤预测的BP神经网络模型
本文建立的坠物撞击下海底管道损伤预测的BP神经网络模型是一种将误差逆向传播的多层前馈神经网络,包括输入层、中间层(也称为隐藏层)和输出层,同层单元之间互不连接。模型的输入层包括坠物撞击能量、管道直径、壁厚、内压和屈服强度、饱和黏土海床不排水抗剪强度6个参数,管道损伤为输出层。输入层6个参数经过中间隐藏层节点作用,与输出层建立非线性映射关系,输出管道损伤预测值。模型结构如图14所示。

图14 BP神经网络结构图Fig.14 BP neural network structure diagram
本文模型的BP神经网络学习过程由正向传播和误差反向传递组成。在正向传播过程中,输入层不进行任何处理,隐藏层对输入数据进行线性与非线性运算,并且通过 Sigmoid 函数将不同大小的输出值控制在(0,1)的范围内,最后将结果传送到输出层,Sigmoid函数为[30]
(3)
式中:x为输入层的6个特征参数;f(x)为处理后的特征参数。
当预测误差较大,即误差达不到神经网络模型设置的精度时,将正向传播的预测值进行反向传播。在误差反向传递阶段,按原来的通路逆向工作,采用梯度下降法对BP神经网络的连接权值和误差进行调整优化,使预测值和真实值更为接近;同时,通过调整学习因子与步长来调节权重矩阵和误差,使误差达到最小。其公式如下[31]:
(4)
式中:ΔWij为输入层与隐藏层之间权重矩阵的误差;n为时间步;η1为主要学习因子;η2为自适应学习因子;φi为输入层输出节点的计算误差;Oj为隐藏层节点输出结果;μ为动量因子;φ为步长;Hp(n)为时间步n的管道损伤值;Hp(n-1)为n-1时间步管道损伤值。
本文采用数值模拟的105组算例结果作为训练样本,以管道直径、壁厚、钢材等级、内压、坠物撞击能量和饱和黏土不排水抗剪强度为输入参数,代入神经网络模型,通过模型计算,输出海底管道损伤,模型的允许误差为10-5。经过模型训练迭代52次,预测结果满足精度要求,由此建立坠物撞击下饱和黏土海床海底管道损伤预测的神经网络模型。
4 BP神经网络模型与已有研究结果的对比验证
文献[16]建立了坠物撞击海底管道数值模型,计算了平铺于黏土海床上海底管道受球形坠物撞击引起的损伤,数值模拟中管道直径0.4 m,管道壁厚12.7 mm,管道屈服强度360 MPa,杨氏模量为2×1011Pa,管道无内压,海床土的弹性模量为5 MPa,坠物能量在0.1~40.7 kJ范围,其10组数值计算结果如表2所示。利用本文神经网络预测模型获得相应的海底管道损伤预测值,也如表2所示。

表2 与文献[16]海底管道撞击模型验证案例对比Tab.2 With documents [16] submarine pipeline impact model validation case
由表2可知,本文神经网络模型预测结果与文献[16]的数值结果最小偏差为0.31%,最大偏差为9.41%。可见,本文模型预测结果与文献[16]的数值结果基本一致。文献[16]数值计算中,部分坠物能量在DNV规范范围之外,这可能是一些结果偏差较大的原因。总体上,本文神经网络模型预测结果可靠。
文献[32]建立的坠物撞击海底管道数值模型,计算了坠物能量范围在10~400 kJ、管道直径0.8~1 m、壁厚17~25 mm、钢材等级X52~X70、管道内压0~8 MPa以及海床土不排水抗剪强度10~200 kPa条件下球形坠物撞击引起的海底管道损伤。本文从文献[32]的数值结果中选取10组作为本文神经网络模型的验证算例,10组算例结果如表3所示。该验证算例的主要参数如下:海床土不排水抗剪强度为10 kPa、土的弹性模量为5 MPa,管道屈服强度为450 MPa,管道无内压。
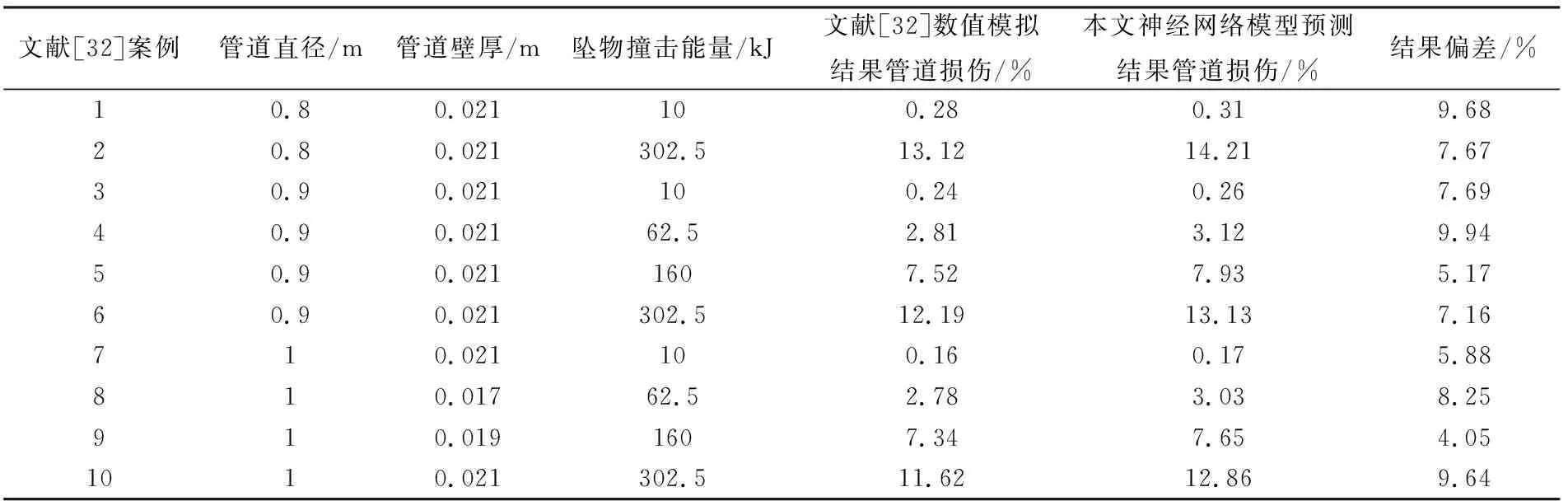
表3 与文献[32]海底管道撞击模型验证案例对比Tab.3 With documents [32] submarine pipeline impact model validation case
由表3可知,利用本文神经网络模型预测海底管道损伤,预测结果与文献[32]的数值结果偏差在10%以内,数值结果基本相符,表明本文构建的BP神经网络计算结果可靠。
5 结 语
本文在ABAQUS下使用显式动力非线性分析方法建立了坠物撞击海底管道损伤的有限元模型,利用该模型开展数值分析,结合实际海底管道工作条件参数变化范围,研究了管道直径、壁厚、钢材等级、内压、土体不排水抗剪强度和坠物撞击能量6个因素对海底管道损伤的影响规律;将6个因素作为输入层参数,以海底管道损伤作为输出参数,以数值模拟结果作为训练样本,通过学习、训练,构建形成了海底管道损伤预测的BP神经网络模型,并对模型预测结果的可靠性进行了验证,得到如下结论。
1)坠物撞击能量越大,管道损伤越大,管道损伤增长速率随坠物撞击能量的增大而趋缓,坠物能量由42.5 kJ增加到197.5 kJ,管道损伤由5.01%增加至17.67%。
2)管道直径从0.7 m增加到0.9 m,管道损伤由16.01%降低到14.36%;管道壁厚由19 mm增加至23 mm,管道损伤从16.52%降低到14.07%。管道直径、壁厚越大,管道损伤越小;钢材等级越高,管道内压越大,管道损伤越小。
3)饱和黏土海床不排水抗剪强度增加,海底管道损伤增加,这主要是由于不排水抗剪强度越大,土体吸收的撞击能量减小,管道吸收撞击变形的能量增加。
4)建立的海底管道损伤BP神经网络预测模型能够较好地预测饱和黏土海床海底管道受坠物撞击的损伤情况。另外,本文数值算例涵盖了常见饱和黏土海床海底管道的工作条件,建立的神经网络模型预测海底管道损伤仅需坠物撞击能量、管道直径、壁厚、钢材等级、内压和海床土不排水抗剪强度6个参数,模型简单、便捷,适用性好,为海底管道损伤预测提供了新思路。
下一步将进一步探究管道埋深、双层管道结构等对海底管道损伤的影响及预测方法。
