基于模糊BN和改进证据理论的车辆故障定位方法

胡 杰，张 潇，魏 敏，，陈 林，卿海华，高长斌

（1.武汉理工大学，现代汽车零部件技术湖北省重点实验室，武汉 430070；2.武汉理工大学，现代零部件技术湖北省协同创新中心，武汉 430070；3.新能源与智能网联车湖北工程技术研究中心，武汉 430070；4.上汽通用五菱汽车股份有限公司，柳州 545000）

前言

随着汽车电子技术的不断发展，汽车功能复杂性日益提高，车载故障诊断系统的出现为故障诊断开拓了新的思路。当车辆发生故障时其自诊断系统会产生故障码（diagnostic trouble codes，DTC）并保存［1-2］，维修人员通过诊断仪读取故障码并对其分析进行故障定位并诊断。然而，由于车辆运行中各电控模块互相进行信息传递，使得维修过程读取的故障码具有驳杂、数量大的特点。同时，实际上故障码产生这一情况本身并不表明故障码自身定义中涉及的部件一定发生了故障，存在着车辆行驶过程中由于环境引起的偶发情况而产生故障码、某些部件受到其它故障部件影响而信号异常产生故障码等情况。面对大量杂乱的故障码导致通过分析故障码来进行精准快速的故障定位并未取得理想效果。

通过分析问题为根据维修过程读取出的大量杂乱故障码推理出源头故障部件，首先考虑贝叶斯网络（Bayesian network）［3］方法。然而，由于故障样本数量少、故障码众多导致贝叶斯网络的条件概率表难以通过样本数据或专家经验生成，故利用D-S 证据理论（D-S evidence theory）［4］，将不同部件在各故障码下发生故障的后验概率看作推理出故障部件的证据，通过融合贝叶斯网络和证据理论解决问题。

李仲兴等［5］构建BN 模型得到不同工况下基于振动和噪声的BN模型后验概率，再通过证据理论将其融合实现轮毂电机的故障诊断。李宏梅等［6］通过构建BN 模型针对汽车网络故障的不确定性进行分析，利用信息融合方法实现发动机的故障诊断。史晓娟等［7］将故障树转化为BN 模型，利用专家评估确定故障与征兆间关系，实现排水系统的故障诊断。上述文献通过专家知识以及样本数据确定BN 的结构与参数，实现了不同领域的故障诊断。但在节点众多且样本数据不足的情况下，确定先验概率和条件概率表等参数是一项工作量巨大且存在不确定性的任务。

陶鹏等［8］提出了一种证据可信度的修正函数用以解决证据信度为零的悖论，再利用支持概率解决证据冲突问题，将其应用于电气设备故障诊断且取得了良好效果。张宽等［9］提出基于Pignistic 概率距离构建相似度的方法对基本概率赋值修正，并引入平均支持度加权优化的证据融合规则，实现对变压器进行故障诊断。夏飞等［10］提出了一种利用证据间相似度构造新证据体并将新旧证据同时合成的方法，实现了燃气轮机振动故障诊断。上述文献均通过引用不同指标衡量证据之间的距离来分析各证据的可信度、相似度以作为证据修正的依据并取得良好的效果，但其均从不同证据间冲突角度考虑，未考虑证据自身存在的不确定性。

考虑到上述所提不足，并为解决由于部件的关联故障而产生大量复杂故障码导致通过分析故障码进行故障定位的准确性差、效率低的问题，本文以某企业某新能源车型的ABS 系统为例，相关售后数据为基础，提出一种基于模糊BN和改进证据理论的故障定位方法。首先根据求援索赔和售后诊断故障码的历史数据以及该车型维修手册构建BN，并通过云模型对其参数进行模糊化。然后将后验概率作为证据，考虑证据的不确定性和证据间冲突，提出融合邓熵和Pignistic 概率距离的修正系数对证据进行修正。最后采用基于矩阵分析的合成规则在降低冲突的同时减小由于证据量多、合成规则复杂带来的计算量大、合成悖论等情况，得到最终故障定位结果，准确高效地实现故障定位。

1 数据来源及处理

1.1 数据内容

本文数据来源于某公司某新能源车型2020 年10 月至2022 年10 月大数据平台存储的售后诊断故障码数据以及售后部门存储的求援索赔数据，该两份数据均以表格形式保存。其中，故障码数据表结构如表1所示。

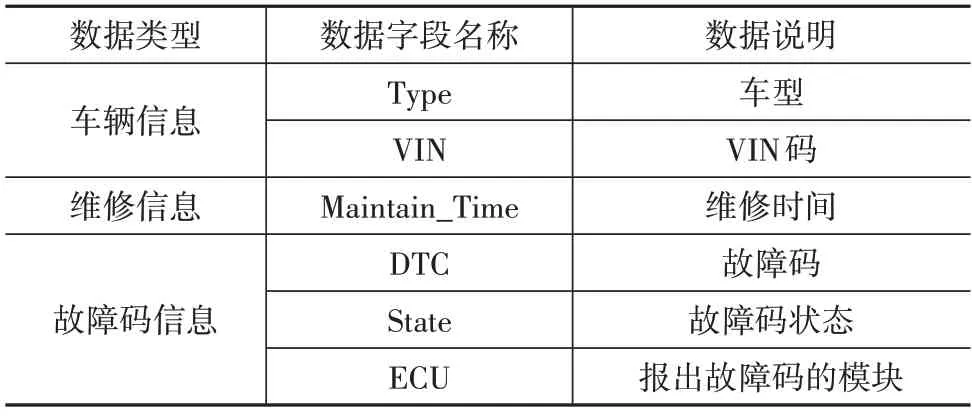
表1 故障码数据分类

求援索赔数据结构如表2所示。

表2 求援索赔数据分类及说明

1.2 数据预处理

1.2.1 故障码数据处理

故障码状态包含当前和历史两种状态，其代表故障码为与该次故障相关或历史诊断遗留。针对售后维修存在着实际故障已解决但部分故障码无法消除的情况，由于这种故障码不影响车辆正常运行，故将该类故障码丢弃处理。

同时，由于存在维修工人误操作导致重复上传的现象，故限制同一车辆诊断事件的时间间隔不得少于3天，对多次上传数据进行去重处理。

此外，由于车辆各模块通过CAN 网络互相收发信息，导致某些故障码会在不同模块重复出现，故将该类重复故障码进行去重处理。

1.2.2 求援索赔数据处理

求援索赔中存在着更换配件与实际故障配件不匹配的问题，由于该类数据不多，故采用人工处理。根据分析处理过程判断故障原因是否准确，若存在问题则对该条数据丢弃处理。对于数据重复上传问题同故障码数据表方法处理。

1.2.3 数据集成

将处理后的故障码数据和求援索赔数据按照车型、VIN 码和维修时间进行集成。经过数据预处理后，得到ABS 系统共327 个案例，共包含4 614 条故障码数据，部分数据如表3所示。

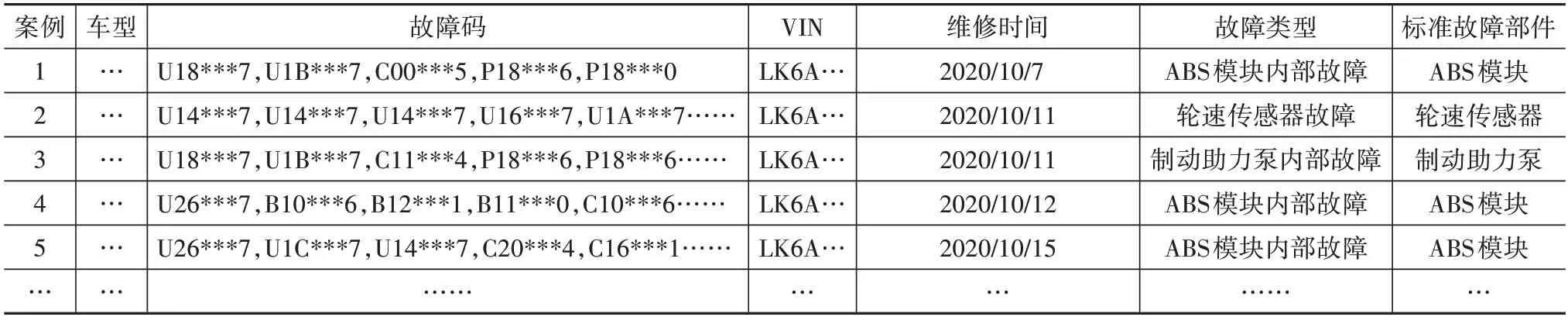
表3 预处理后故障历史数据

2 故障定位模型构建

本文提出一种基于模糊BN 和改进证据理论的车辆故障定位方法。所构建的故障定位模型流程如图1所示，具体步骤如下。

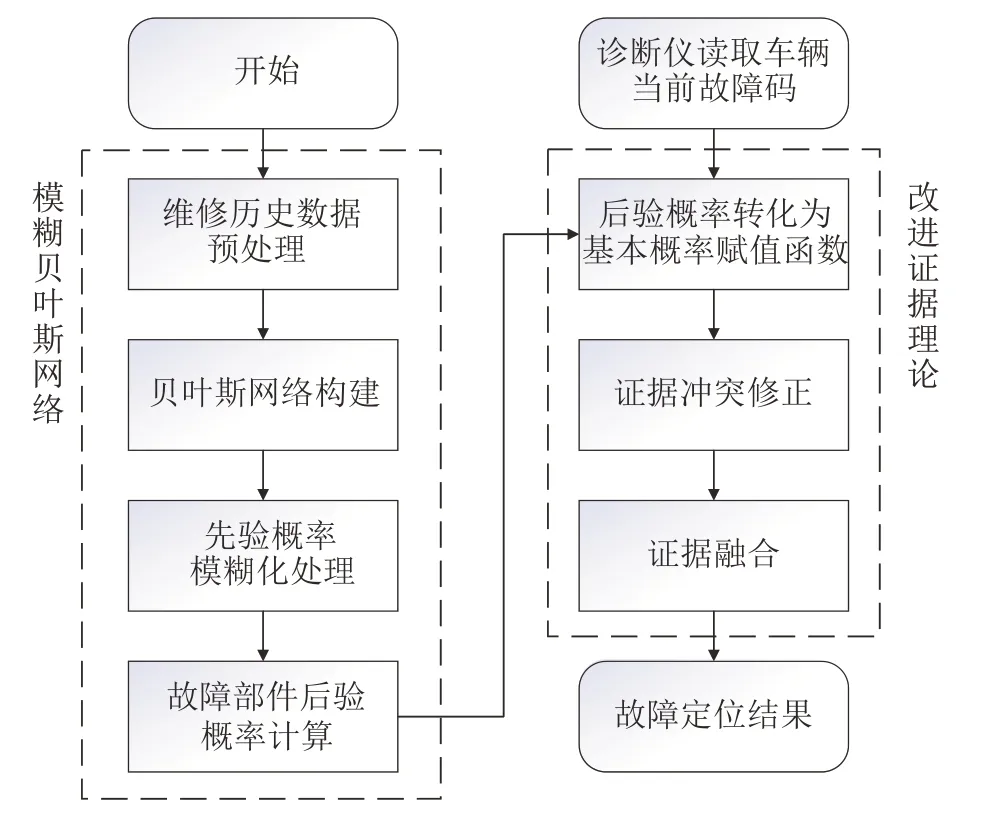
图1 故障定位模型流程图

（1）模糊BN 构建。将故障码作为故障征兆，通过历史数据和专家经验确定BN结构，并通过云模型数字特征模糊化其先验概率。

（2）基本概率赋值转化。将模糊BN故障部件后验概率作为各条证据的基本概率赋值。

（3）证据修正。融合邓熵和Pignistic 概率距离作为修正系数对证据的不确定性和证据之间冲突进行修正。

（4）改进合成规则。采用基于矩阵分析的合成规则将修正后的基本概率赋值合成，得到各部件故障的可能性。

（5）故障定位结果。比较各部件故障的可能性，最大值对应的部件即为最终故障定位结果。

2.1 模糊BN

根据历史样本数据以及维修手册确定整个系统中可能发生故障的部件以及故障码，将故障码作为故障征兆，通过历史样本数据确定各故障征兆与故障部件之间的关联。

故障部件节点与故障码节点通过有向边建立关联。以ABS 系统为例，本研究所构建的BN结构如图2 所示，其分为两层结构，上层为可能发生故障的部件，下层为全部可能出现的故障码。

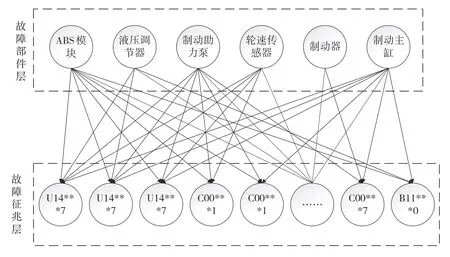
图2 BN网络结构图

由于节点的故障概率是通过历史样本数据获取，而故障数据属于小样本数据，故采用云模型模糊化先验概率。

云模型作为一种在概率论和模糊理论基础上发展的综合模型，刻画了数值之间随机和模糊的性质，在描述不确定信息上极具优势［11］。其具有3 个数字特征：期望Ex、熵En和超熵He。期望Ex代表论域空间中云滴分布的期望值；熵En代表云的跨度，反映云分布的不确定性；超熵He代表熵的离散程度，反映熵的不确定性。

云生成器为标准云生成算法，按其功能可以划分为正向云生成器与逆向云生成器。正向云生成器需要预先设置数字特征（Ex，En，He）以及生成的云滴数量，输出云图像，过程如图3所示。

图3 正向云生成器

图4 云模型图像

逆向云为正向云生成的逆过程，通过输入已有的样本分布，输出其对应的数字特征（Ex，En，He），过程如图5所示。

图5 逆向云生成器

假设两个标准云分别为Ci和Cj，云模型的算术运算规则［12］为

根据已有样本和经验通过逆向云生成器输出各故障部件先验概率的云模型数字特征，以先验概率的数字特征代替先验概率作为模糊处理，通过云模型的算术运算规则公式和贝叶斯公式计算出各部件在不同DTC 下发生故障的后验概率数字特征。其中贝叶斯公式如式（6）所示。

式中：p(Fi)为基本部件故障的先验概率，由历史数据得到；p(DTCj|Fi)为在已知实际故障部件的前提下某故障码出现的条件概率。

最后将后验概率的数字特征依次通过正、逆向云生成器迭代10 次体现其不确定性与随机性，以其迭代10 次所得数字特征期望Ex的平均值作为最终后验概率。

2.2 改进证据理论

将已构建的BN 的标准故障部件后验概率归一化，转化为证据的基本概率赋值。由于传统D-S 证据理论存在着未考虑证据自身权重，忽略冲突中所蕴含的信息等缺点，难以直接进行实际应用，故本文提出了融合邓熵和Pignistic 概率距离的修正系数，对证据的冲突部分重新分配基本概率赋值，以实现准确合理的故障定位。

2.2.1 证据确定程度

邓熵（deng entropy）［13］是Deng 提出的一种不确定性度量方法，他受到香农熵的启发，在测量不确定度时考虑了基本命题的基数造成的影响，提出了邓熵的概念。其具体公式如下：

式中|A|是A的基数。邓熵具有|A|越大则ED越大，其不确定程度越大的性质。

根据式（7）可计算出各证据自身的不确定程度。由于邓熵ED的值越大，不确定程度就越大，则可定义（1-ED）为证据的确定程度Ens。

2.2.2 证据可信度

Liu 在证据距离量化过程中引入Pignistic 概率距离［14］，用以描述证据之间的冲突程度。其定义Pignistic概率函数BetPm(A)为

式中|A|是A的基数，则两个独立的证据主体BetPm1和BetPm2的Pignistic概率距离为

由上式可知，Pignistic 概率距离的范围为［0，1］且具有值越大则冲突越明显的性质。

通过式（8）和式（9）可计算出各证据之间冲突程度。分析Pignistic 概率距离的性质则可将定义为m1和m2一致性程度，其值越大则一致性越强。定义各证据可信度Beli的计算公式如下：

2.2.3 证据修正

依据证据的确定程度与其可信度，将二者结合并与所得最大值相除可得证据的相对权重，即作为修正系数。

则修正后的基本概率赋值为

2.2.4 证据合成规则

传统证据理论合成规则如下式所示：

式中k为冲突因子，代表证据之间的冲突程度，其范围为［0，1］，k值越大则冲突程度越大。

传统合成规则具有面对高冲突证据融合会产生悖论，且当证据和基本命题的数量增加时其合成计算的复杂程度呈指数趋势增加等缺点。故采用基于矩阵分析的合成规则［15］在降低冲突的同时减少计算量，其伪代码如表4所示。

表4 改进合成规则伪代码

3 算例分析

本文以某企业新能源某车型的ABS防抱死系统为例，对已处理好的数据进行切片操作，按4∶1 的比例随机选取训练集260个案例、验证集67个案例，进行故障定位的应用研究。

选取验证集中某简单案例为例进行故障定位模型演示，该案例的具体数据如表5所示。

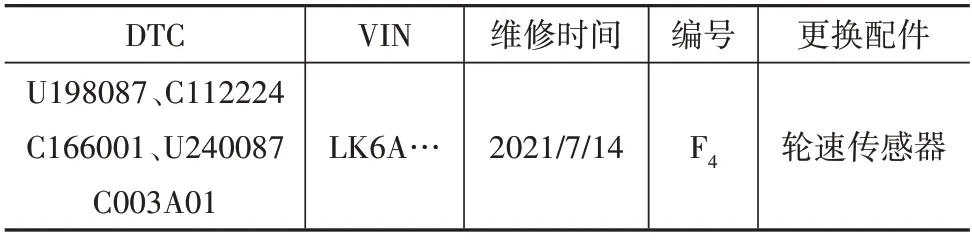
表5 演示案例数据展示

3.1 模糊BN构建

在实际售后维修过程中，由于服务站受技术水平限制，大多部件出现损坏后服务站采取的措施更多的是对故障部件整体进行更换，故根据求援索赔数据中ABS 系统更换的部件，将发生故障后被更换的部件整体定义为标准故障部件F1～F6。根据该车型维修手册以及历史维修数据构建演示案例的BN，标准故障部件F1～F6作为故障部件层，故障码作为故障征兆层，如图6所示。

图6 演示案例BN

根据专家知识并结合售后维修数据，对各标准部件故障出现概率统计，得到各标准故障部件的先验概率云模型数字特征，并以其代替先验概率作为模糊化处理，如表6所示。

表6 标准故障部件的先验概率数字特征

通过正向云生成器生成各标准部件的云图像，云滴数设置为5 000即可看出各朵云的大致形状，如图7所示。

图7 标准部件云模型图像

本案例中，在单一部件发生故障时某故障码出现的条件概率P(DTCj|Fi)如表7 所示，其余子节点的条件概率可按相同方法计算。

表7 子节点的条件概率

根据贝叶斯公式可计算出各标准故障部件在不同DTC 下发生故障的后验概率数字特征。将所得到的后验概率数字特征通过正、逆向云生成器迭代10 次后，取期望的均值作为后验概率，所得后验概率如表8所示。

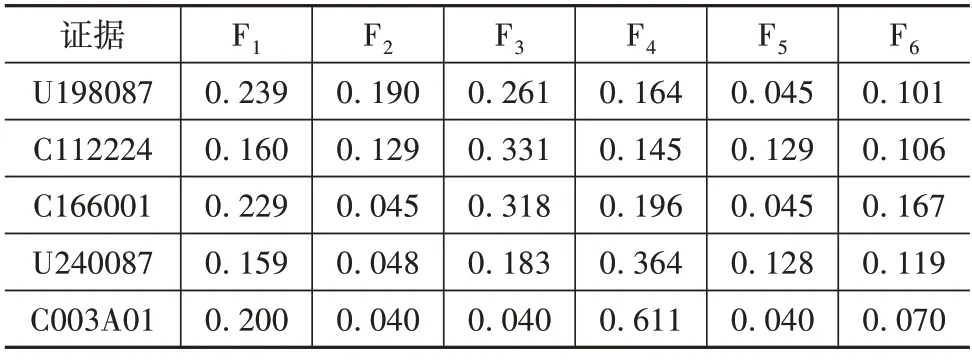
表8 节点Fi的后验概率

3.2 证据修正计算

将故障部件在本案例所涉及到的故障码的后验概率作为证据的基本概率赋值，并对其进行修正处理。根据专家经验将各标准故障部件的故障基数分别设置为A=｛4，2，2，2，1，1｝。

3.2.1 确定程度计算

由式（7）和确定程度定义可分别计算出邓熵和证据的确定程度，如表9所示。

表9 证据确定程度

3.2.2 可信度计算

对各证据的基本概率赋值之间的冲突程度计算，根据式（8）和式（9）则可以计算出各条证据之间的Pignistic概率距离矩阵，如表10所示。

表10 证据间Pignistic概率距离

根据式（10）将所求得的Pignistic 概率距离转化为各条证据的可信度，如表11所示。

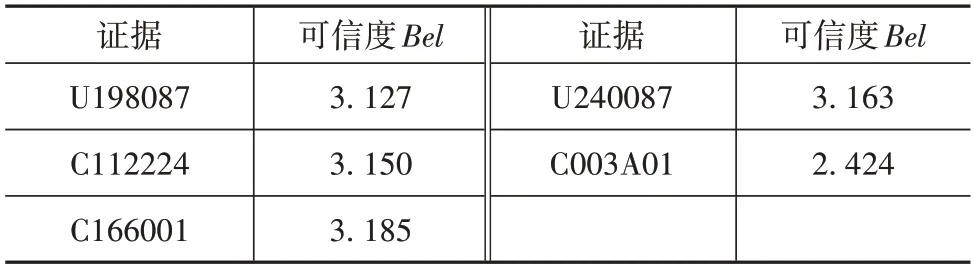
表11 证据可信度

3.2.3 基本概率赋值修正

根据式（11）可计算出相对修正系数矩阵：η=［0.9635，0.9881，0.9963，1，0.7818］。利用式（12）可计算出各证据修正后的基本概率赋值，其中最后一列为

以传统D-S 证据理论中的冲突因子k作为评价指标，对比采用不同方法进行相似度计算并修正后的各证据之间冲突程度，其中包括Wasserstein 距离［16］修正、Jousselme 距离［17］修正、Pignistic 概率距离［18］修正和本文提出的方法，具体效果如图8所示。

图8 不同方法修正后效果图

通过分析图8 可发现，本文提出的方法虽然面对前4 条修正后的证据之间冲突程度减少效果略逊于单独以Pignistic 概率距离进行修正的方法，但是修正后的第5 条证据与其他证据之间的冲突程度显著下降。通过分析邓熵得出的证据确定程度可知，第5 条证据相比于其他证据的确定程度更高，则更应该减少第5 条证据与其他证据之间的冲突程度，故从总体角度认为本文所提出的证据修正方法效果更好。

3.3 证据融合

最后根据基于矩阵分析的证据合成规则将修正后的基本概率赋值进行融合，得到故障定位结果，如表12所示。

经比较分析故障可能性可知，通过故障定位模型得出本案例应为轮速传感器发生故障，故障部件定位结果与实际案例一致。

3.4 方法准确性分析

将本文提出的方法应用于验证集进行准确性验证，得到各标准故障部件发生故障时的故障定位准确率，如表13所示。

表13 标准故障部件故障定位准确率

经对故障定位的错误案例分析发现，虽然定位结果与实际故障部件不符，但实际故障部件的可能性大小基本排在自大到小的第二位，仍可以在一定程度上为故障定位提供参考，故认为本文提出的方法在故障定位的应用上具有有效性。

3.5 改进方法结果对比

为了进一步验证本文提出方法的优势，将传统DS 证据理论、邓勇加权平均法［19］和采用基于矩阵分析的合成规则将未修正证据、分别以Wasserstein 距离、Jousselme 距离和Pignistic 概率距离计算相似度并修正后的证据合成以及本文提出的方法均应用于验证集并进行比较，统计准确率和合成平均耗时情况，结果如表14所示。

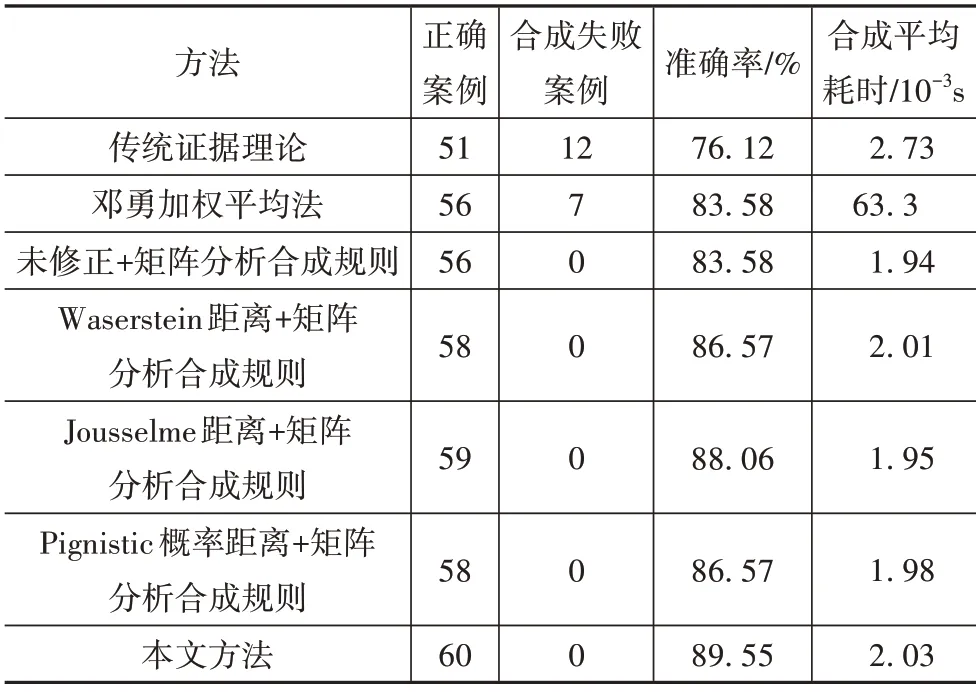
表14 不同方法结果比较

经分析发现合成失败案例均为故障码数量较多的案例。比较采用不同方法的故障定位结果可发现，本文方法在提高准确率的同时实现了降低证据合成所需时间，避免了故障码较多时合成失败的情况，故认为本文方法具有可行性且更具优势。

4 结论

本文针对由于车辆部件关联故障而产生大量复杂故障码，导致通过分析故障码定位源头故障部件效率低的问题，提出基于模糊BN和改进证据理论的故障定位方法。首先通过根据求援索赔和售后诊断故障码的历史数据和专家知识构建BN，并用云模型对其先验概率模糊化；然后将模糊BN后验概率作为改进证据理论的基本概率赋值输入，将邓熵和Pignistic概率距离融合作为修正系数进行证据修正，并采用基于矩阵分析的证据合成规则保证无合成失败情况的同时减少计算量，得到最终故障定位结果；最后通过实际案例验证了该方法的可行性。所提方法有效地解决了售后维修过程中面对大量故障码时分析故障部件困难的问题，提升了故障定位的效率和准确率，为售后维修人员提供帮助。