基于声学传递函数和正则化方法的高频声功率载荷反求研究
2023-11-09郝耀东邓江华陈达亮
庄 超,王 欢,郝耀东,邓江华,陈达亮
(1.高端工程机械智能制造国家重点实验室,徐州 221004;2.江苏徐工国重实验室科技有限公司,徐州 221004;3.中汽研(天津)汽车工程研究院有限公司,天津 300399)
前言
声功率是表征声源特性的主要指标,反映了声源声辐射的大小和频率分布。获得各个声源的声功率,是机械产品声学性能开发的重要组成部分[1]。
声源声功率可以基于试验测试得到[2]。将声源,如发动机、冷却风扇等置于半消声室中,控制其转速、负载等工况参数,在其周围布置一定数量的传声器,通过测试得到的声压级曲线计算声功率。
试验测试声源声功率存在以下缺点:需要将声源独立拆解出来进行测试;需要专业的工装夹具对声源进行固定;需要专业的设备对声源的工况进行精确控制;需要大量的时间和成本进行测试工作。以上缺点注定了声功率试验需要耗费不菲的时间和成本。
与试验测试方法相比,载荷反求方法是一种耗费成本极低的方法。只需要在整机上进行测试,不需要进行声源拆解和固定,也可以通过整机运行控制工况。载荷反求方法的研究始于20世纪70年代,最早用于军事和航空领域。1979 年,Bartlet 和Flannelly[3]就将载荷反求技术用于直升机主轴动态力的识别。Desanghere 和Snoey[4]基于模态法对某轿车底盘的梁结构进行载荷反求试验研究,还详细地讨论了不同模态参数、测量噪声和模态数目等因素对载荷反求结果的影响。LMS 公司[5]将载荷设备方法集成到自己的软件中,实现了基于车辆参考点响应信号和传递函数来识别载荷力。
但是,现有的载荷反求方法在应用范围和原理都存在一定的局限性。在应用范围方面[6-7],目前基于工况响应数据反求激励载荷的载荷反求方法主要应用于乘用车、航空航天设备、船舶等领域,在工程机械领域未见应用。工程机械座舱体积小且密封、声学包布置等条件难以得到保证,因此参考乘用车的载荷反求方法采用内场噪声进行载荷反求具有较大的误差。在原理方面[8],目前载荷的识别均在低频上进行识别,现有的载荷识别方法在高频领域由于频率点过多、计算量过大而罕有应用。
本文提出了一种基于声学传递函数(acoustic transfer function,ATF)和正则化方法的高频声功率载荷反求方法。建立了高频声学传递问题模型,推导了单声源和多声源状态下的声源声功率、ATF 和接受体声压级之间的关系;引入了正则化方法避免矩阵奇异值放大测试误差;采用L 曲线准则计算正则化参数,实现了高频的声功率载荷反求。采用该方法对某挖掘机两种工况下的声源声功率载荷进行了反求,并将反求结果和试验测试得到的声功率进行了对比,验证了方法的准确性。
1 高频声学传递问题模型
1.1 单声源模型
高频声学传递问题模型包括声源、传递路径和接受体3 个组成部分。声源发出声音,通过传递路径,最终被接受体所接受。声源发出的声音采用声功率或声功率级进行描述,接受体接收到的声音采用声压或声压级进行描述,而传递路径对声学传递的作用则通过声学传递函数来进行描述。
声学传递函数fa被定义为接受体声压p与声压体积加速度Qa的比值,ATF 往往采用其对数形式Lf来进行表示。
式中p0表示参考声压,p0=2×10-5Pa。
在自由场中,点声源的声功率Π可以表示为
式中:ρ、c分别表示空气密度和声速;Qa*表示体积加速度Qa的共轭,Qa·Qa*即为体积加速度Qa自功率谱。
在工程问题中,声功率Π和声压p也经常被表示其成对数形式Lw和Lp。
式中Π0=10-12W。
联立式(1)~式(5),即可求得单声源激励下声功率级、ATF以及声压级之间的关系式。
1.2 多声源模型
在多声源模型中,存在m个声源和n个接受体,共存在m·n个声学传递函数,其中第i个声源的声功率级、第j个接受体的声压级和第k个传递函数分别用Lw,i、Lp,j和Lf,ij来表示。
在高频宽带范围内,声压的相位分布具有随机性。因此,对于第j个接受体,其总声压pj的平方可以表示为所有声源引起的声压的平方和。
式中pj,i表示第i个声源引起的接受体j的声压。并且有
式中Lp,j,i表示第i个声源引起的接受体j的声压级。
将式(5)和式(7)代入式(8)中,可得接受体j的声学传递方程。
将式(9)改写为
将所有接受体的声学传递方程表示为矩阵形式:
其中:
目前载荷反求的难点主要是识别均在低频频率上进行,现有的载荷识别方法在高频领域由于频率点过多、计算量过大而罕有应用。而式(11)是在宽频范围内计算的,例如400~10 000 Hz 范围内,现在的载荷识别方法需要逐个频率进行计算,若分辨率为100 Hz,则需要计算9 600步;而式(11)是在1/3倍频程上进行计算的,只需要计算15 步。若采用现有的载荷设备方法,计算6 000 Hz处的声学传递情况,则只能代表6 000 Hz 一个频率;而采用式(11)进行6 000 Hz处的计算,则能够代表5 345~6 734 Hz范围内的以6 000 Hz为中心的整个1/3 倍频程频段内的平均的声学传递情况。
依据式(11)已知各声源的声功率级和各声学传递函数,即可求得各个接受体的声压级。
2 高频声功率识别的正则化方法
2.1 载荷反求的正则化方法
由式(11)可知,通过测试接受体声压向量Mp和传递函数矩阵Mf,即可反求得到声源声功率向量Mw。但是,测试得到的声压Mp,test不可避免地存在误差Mp,error,即有
对矩阵Mf进行奇异值分解,可以得到
式中:ui、vi分别为Mf的左奇异列向量和右奇异列向量;σi为矩阵的第i个奇异值。
若Mf的逆矩阵存在,则反求得到的声功率向量Mw,test可以表示为
式中:Mw为声功率精确解;ηi为Mp,error中的第i个测试误差。
由式(17)可知,当测试水平一定时,传递函数矩阵Mf的奇异值σi会放大测试误差,导致声功率计算结果出现严重偏离。正则化方法的引入可以避免这一情况的发生。
采用截断奇异值分解(TSVD)的正则化方法进行声功率的反求,即舍弃式(17)较小的奇异值。即令
其中
式(19)即表示舍弃平方值小于ϕ的奇异值。
2.2 正则化方法参数的选取
由式(18)可知,正则化参数ϕ的选择会直接影响声功率的求解结果,合适的ϕ需要同时满足准确性和稳定性的要求。前者要求的值尽可能小,从而保证测试与反求的临近程度,后者要求Mw,test的模在一定的范围之内,保证求解结果的稳定性。
采用L 曲线准则求解正则化参数,在对数尺度下绘制曲线,以为横坐标,为纵坐标。这条曲线将呈现一个明显的L形状,L 曲线的拐点对应的ϕ值即为最佳的正则化参数值。
3 算例
3.1 某挖掘机高频噪声响应与ATF测试
以某挖掘机为研究对象。挖掘机在工作状态下主要包括发动机、冷却风扇、进气口、排气口4 个声源,如图1 和图2 所示。选择GBT 25612—2010《土方机械声功率级的测定 定置试验条件》[9]中规定的挖掘机测量面上传声器的6 个位置为响应点,如图3 所示。图3 中r=10 m,且各响应点具体坐标位置如表1 所示,坐标原点取挖掘机工作状态回转中心点。
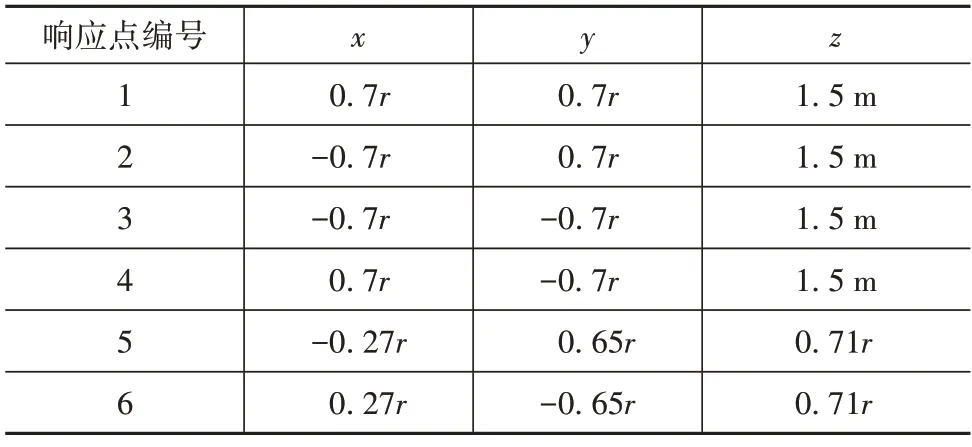
表1 挖掘机响应点坐标
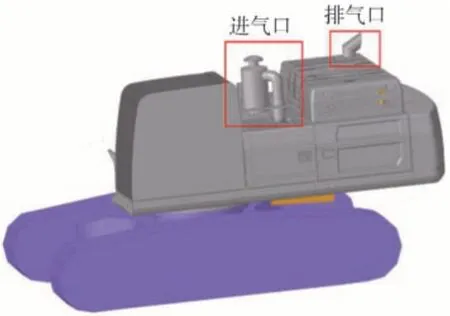
图2 挖掘机的进气口和排气口
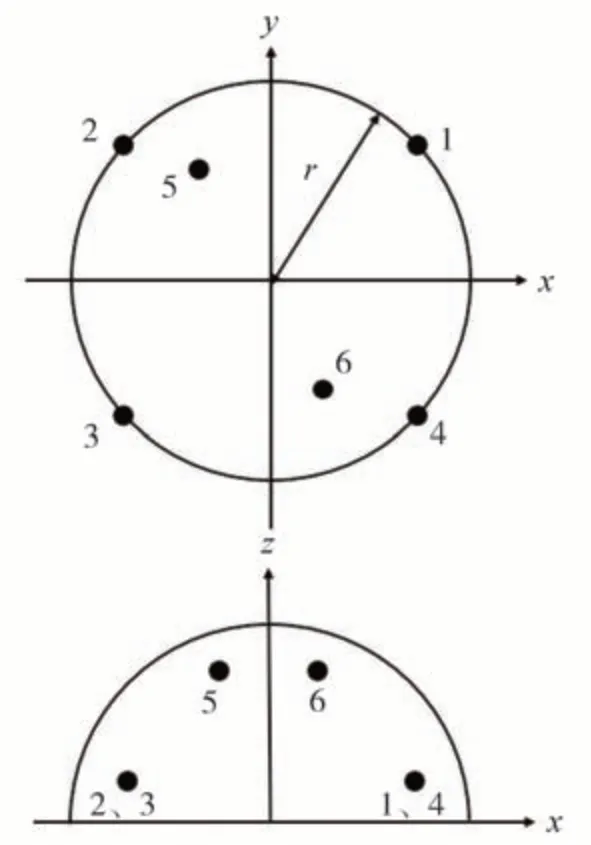
图3 挖掘机响应点位置示意图
将挖掘机放置在半消声室中,保证背景噪声低于30 dB。根据传递函数的互易性原理,将体积声源分别布置在6 个响应点位置,将传声器布置在发动机、冷却风扇、进气口和排气口位置,如图4 所示。通过式(3)和式(6)即可得到声源到响应点的ATF曲线,如图5 所示。需要注意的是,每个声源均布置多个传声器,传声器位置分别布置在声源上、下、前、后、左、右6 个平面,将声源包裹起来,最后得到的声源到响应点的ATF曲线为每个传声器测得的ATF曲线的平均值。

图4 传声器布置
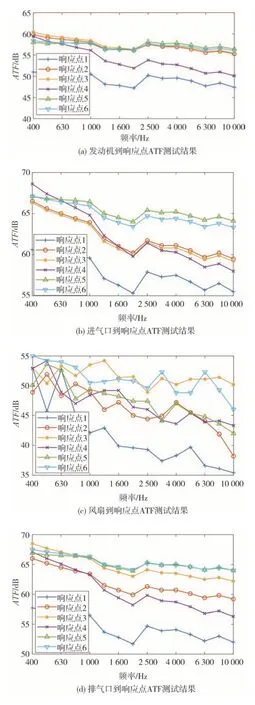
图5 ATF测试结果
同时,测试挖掘机在发动机怠速-风扇自适应转速、发动机最高转速-风扇最高转速两个工况下各响应点的声压级,如图6所示。
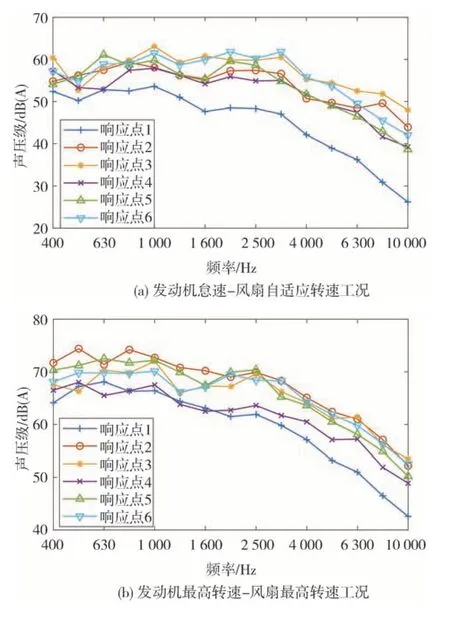
图6 响应点声压级测试结果
3.2 挖掘机高频声功率载荷反求
分别将测试得到的ATF结果和两个工况下的噪声响应结果代入式(18)中,并根据L 曲线准则选择正则化参数。发动机怠速-风扇自适应转速下400 Hz得到的L 曲线如图7 所示,选择正则化参数值为183。

图7 发动机怠速-风扇自适应转速400 Hz频段L曲线
进一步可求得发动机怠速-风扇自适应转速、发动机最高转速-风扇最高转速两个工况下发动机、冷却风扇、进气口和排气口的声功率级,如图8 和图9所示。
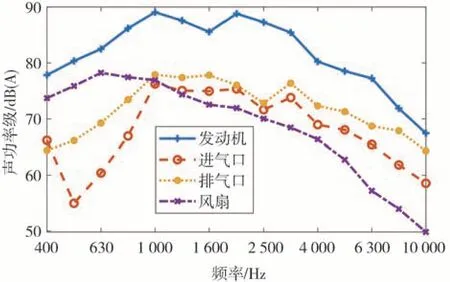
图8 发动机怠速-风扇自适应转速下的声源声功率级
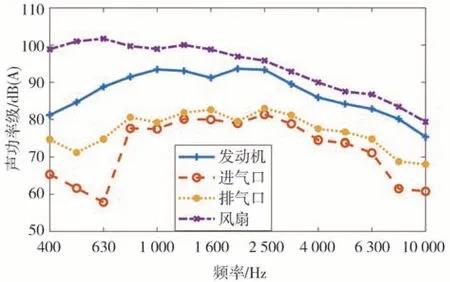
图9 发动机最高转速-风扇最高转速下的声源声功率级
在半消声室中采用9 点法直接测量不同转速下的发动机、风扇声功率级,如图10所示。

图10 发动机声功率直接测试
将反求得到的声功率级和直接测试数据进行对比,如图11~图14 所示。由图可知,采用基于声学传递函数和正则化方法的高频声功率载荷反求方法得到的各声源声功率和直接测试相比误差在2 dB 以内,目前高频仿真中,仿真和试验误差控制在正负3 dB 以内即可表示模型准确,因此该方法具有较高的精度,可以准确地识别出不同工况下的声源声功率。
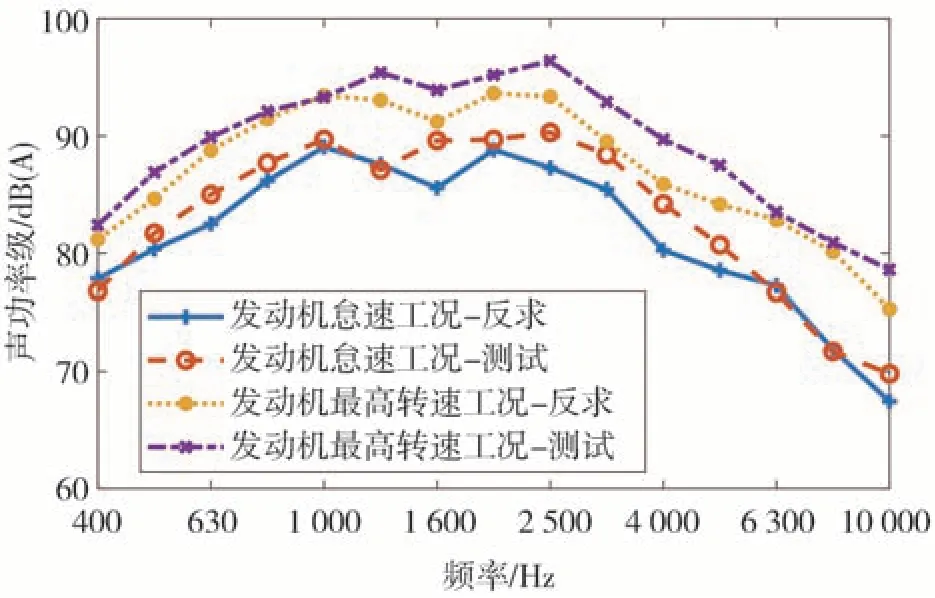
图11 发动机声功率
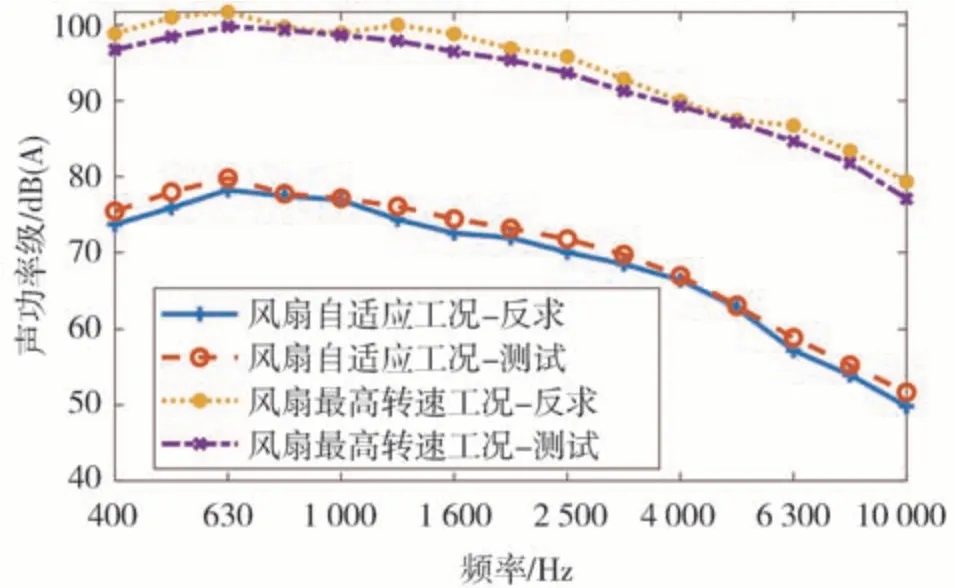
图12 冷却风扇声功率
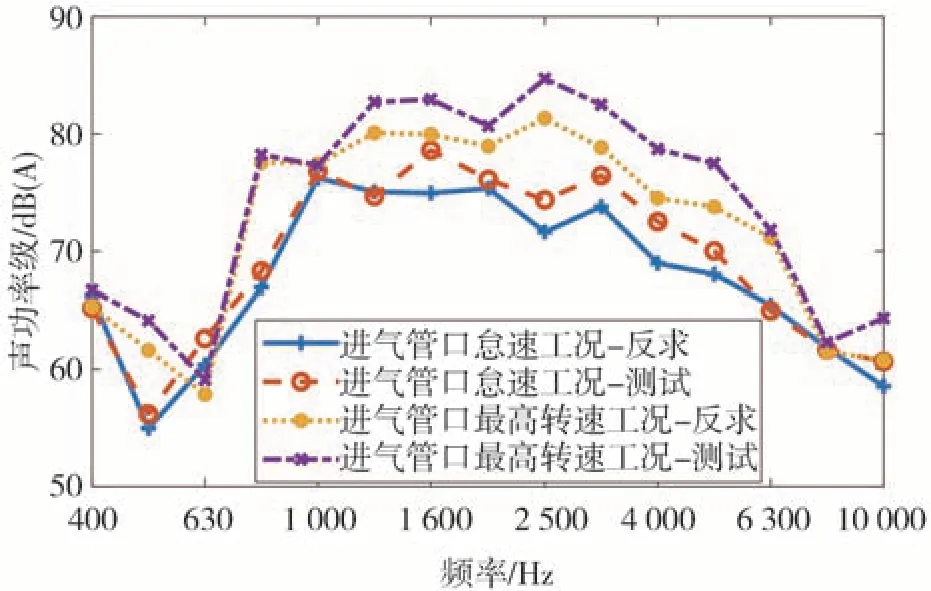
图13 进气管口声功率
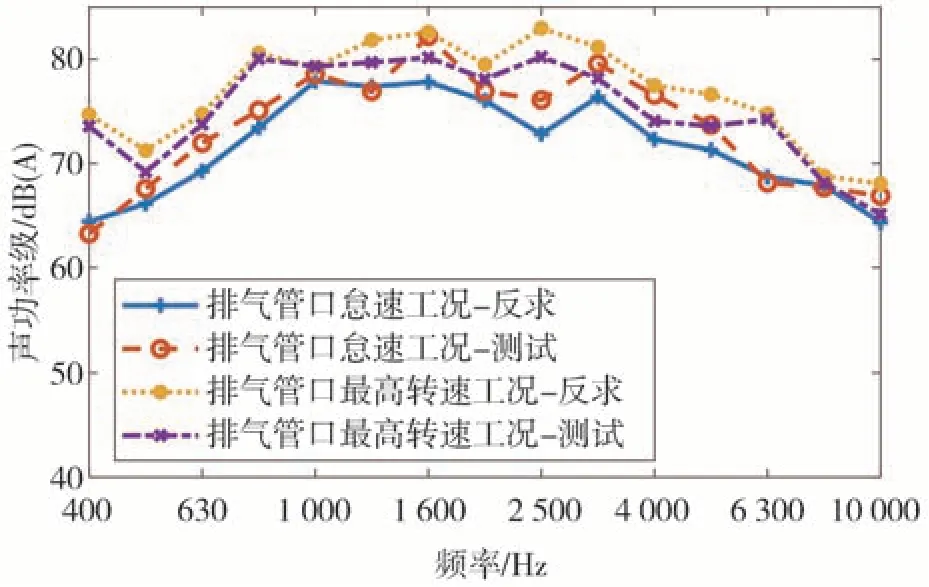
图14 排气管口声功率
4 结论
本文提出了一种基于声学传递函数和正则化方法的高频声功率载荷反求方法。建立了高频声学传递问题模型,推导了单声源和多声源状态下的声源声功率、ATF 和接受体声压级之间的关系;引入了正则化方法避免矩阵奇异值放大测试误差;采用L曲线准则计算正则化参数,实现了高频的声功率载荷反求。
(1)该方法避免了声功率试验测试方法需要拆解、固定声源,以及控制声源工况参数的缺点,可以节省大量的时间和成本;
(2)该方法通过高频声学传递模型的推导,补充了以往频域载荷反求在高频问题上计算了过大(覆盖的频率点过多)的不足;
(3)以某挖掘机为例对该方法进行了验证,测试了挖掘机的声学传递函数和不同工况下的噪声响应,对4 个声源的声功率进行了反求,并将反求结果和直接测试得到的声功率进行了对比,对比结果显示,本文提出的方法具有较高的精度,可以实现高频声学载荷的高精度反求。
