双电机耦合驱动系统构型分层设计方法*
2023-11-09李学良赵志福杨树军彭增雄
李学良,赵志福,杨树军,彭增雄
(1.燕山大学,河北省特种运载装备重点实验室,秦皇岛 066004;2.北京理工大学,坦克传动国防科技重点实验室,北京 100081)
前言
新能源汽车已成为全球汽车产业转型发展的主要方向和促进世界经济持续增长的重要引擎[1]。得益于国家纯电驱动战略的实施,我国纯电动汽车技术水平显著提升,汽车产业基本实现电动化转型[2]。双电机耦合驱动系统是一种新型集中式电驱动系统,具有以下特点:采用双电机的形式能够减小径向尺寸,便于布置;定轴轮系工作可靠、成本低;某一电机发生故障时,车辆仍可保持正常行驶,可靠性强;可实现动力不中断模式切换,提高车辆舒适性和动力性;双电机协同工作,可实现不同负载下双电机的高效驱动,经济性好[3-6];结构更为紧凑,所需元件更少,能达到轻量化的效果,减小占用空间和整车质量。但因双电机耦合驱动系统构型具有多自由度、多源驱动等特性,导致构型内部传动路线复杂、相互耦合,设计过程无规律可循。
构型不仅关系到车辆动力性,作为能量管理的基础,也决定了算法选择和优化潜力[7-10]。近年来,构型方案的生成、同构、优选等问题深受国内外学者的重视。Kim 等[11]提出了一种基于复合杠杆模型的行星排传动系统构型的优选方法,该方法采用全设计域搜索和多目标构型选择。Zhang 等[12]分析Prius和Volt 所采用双电机行星排传动系统,通过加减执行机构的方法得到了改进的双电机单行星排耦合传动系统构型。符升平等[13]提出了一种基于拓扑特征演化分析的行星变速机构构型综合方法。Li等[14]提出一种车用多输入多自由度定轴齿轮传动构型的综合方法,根据轴和齿轮的连接关系定义了可变连接和固定连接,并以其属性作为构型初步筛选的条件。针对行星齿轮组件与行星齿轮组之间连接方式的多样性,Li等[15]提出了基于规则分析的筛选方法,用于混合动力履带车辆的构型设计筛选,将所有候选构型方案进行分类,减少搜索规模并提升搜索效率。Wen等[16]针对新能源多动力源拖拉机在设计和参数优化过程中须考虑到静态指标和电机工作高效区间的分布以及拖拉机在各种工况下的动力需求,提出了一套新型电动拖拉机双电机功率耦合驱动系统设计方法。Yang 等[17]提出了一种基于层次拓扑图论理论的动力总成配置方案设计方法。胡建军等[18]通过拆分并重组单行星排功率输出/输入式两种混合动力系统以生成基础拓扑结构方案,提出一种单行星排功率分流式混合动力系统构型优化设计方案。此外,针对单行星排和双行星排在拓扑过程中的同构问题,杨亚联等[19]采用行星耦合机构邻接矩阵和构件邻接矩阵的组合来描述图论模型,提出根据邻接矩阵输出编码来判断传动系统的同构方案。
目前相关研究多针对模式相对单一、挡位较少的行星齿轮传动,未涉及换挡过程的动力中断问题,难以应用于具有多自由度、多模式、多挡位的双电机耦合驱动系统的构型设计。
1 双电机耦合驱动系统分层设计流程
1.1 功能需求分析
电动商用车通常须匹配多个挡位以覆盖车速和转矩区间,相比单电机驱动系统和传统双电机驱动系统,双电机耦合驱动系统在布置、成本、可靠性、舒适性、经济性等方面均具有明显优势。在构型设计阶段须考虑两方面功能需求:一方面为双电机可单独驱动也可同时驱动;另一方面为在一个电机换挡时,另一个电机仍可传递动力。
以我国重汽某款单电机驱动4挡商用车为原型,现匹配的某3+4 型双电机耦合驱动系统,如图1 所示。该构型中电机EM1 有4 条动力传递路径,电机EM2有3条动力传递路径,电机EM1的4条动力传递和电机EM2的3条动力传递路径通过耦合形成6条耦合路径,其中同步器AB和CD成对布置,同步器E和F单独布置,操纵序列如图2 所示,其中C、EF、D 电机EM2单独工作,ACE、AF、BF、BDE电机EM1单独工作,ACE、ACF、AEF、BEF、BDF、BDE双电机耦合工作。
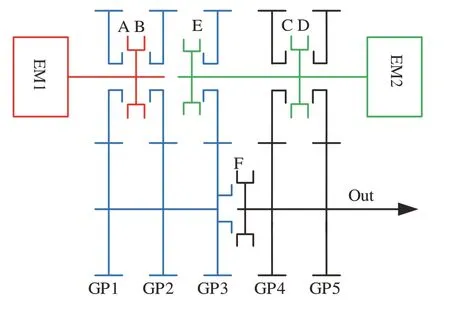
图1 某3+4型双电机耦合驱动系统方案
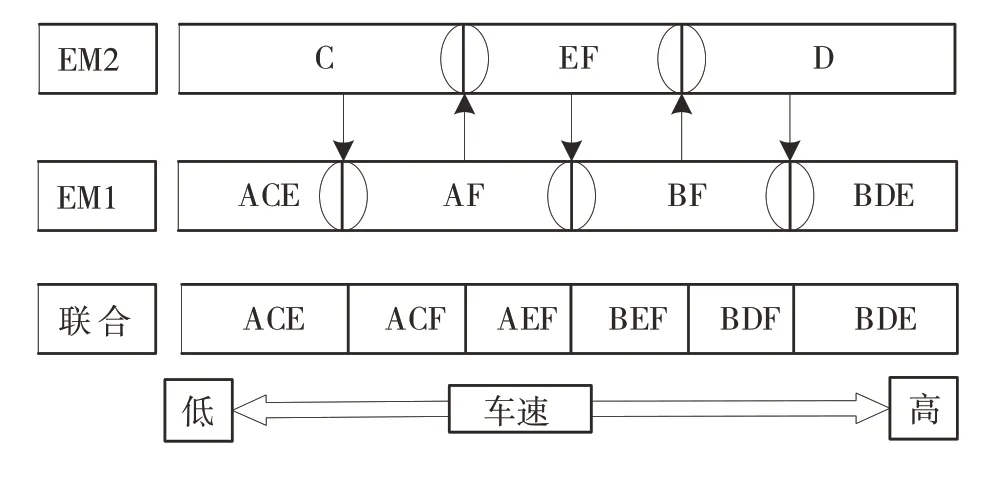
图2 操纵序列
1.2 分层设计流程
双电机耦合驱动系统构型设计的目标为在获得功能需求,即动力传递路径(3+4)且双电机可耦合驱动的前提下,采用便于执行的操纵序列与紧凑的齿轮与轴的布置。其中,操纵序列是功能需求的方式,并不涉及到齿轮与轴的布置、操纵元件布置等传动机构的具体结构。
为此,本文将双电机耦合驱动系统构型设计分为功能生成层与结构衍生层,功能生成层抛开构型具体结构,从功率流角度分析运动特征,基于可实现3+4 模式的双电机功率传递路线及无动力中断模式切换等功能需求,建立功能分析图论模型,进行功能分析,根据路径耦合条件进行优选,获取操纵序列。结构衍生层基于功能需求,定义基本构型、齿轴构型等概念,根据输入轴和输出轴的位置,确定系统所需的轴系和固定连接结构,在功能生成层的基础上,以优选序列中的子路径确定变连接结构的属性和相对位置,依次进行固定连接结构到基本构型再到齿轴构型的衍生,布置操纵元件,最终获得优选构型,设计流程如图3所示。

图3 设计流程
2 功能分析图论模型与功能生成
2.1 功能需求与图论模型
当所有操纵元件处于非工作状态时,将驱动系统中具有唯一确定的相互运动关系的构件定义为子机构,如图1 中红色的子机构定义为F1,绿色的子机构定义为F2,黑色的子机构定义为F3,蓝色子机构定义为F4。子机构之间通过操纵元件连接,则双电机耦合驱动系统构型可由子机构和连接各个子机构的操纵元件构成。若将子机构作为一个整体来考虑,操纵元件就转化为子机构之间的通道。子机构中与操纵元件相连接的构件的差异造成了子机构与子机构之间传动比的差异。如图1 中连接子机构F1和子机构F4的操纵元件有A 和B,即一个同步器的两种形态,其中操纵元件A 连接齿轮对GP1,操纵元件B连接齿轮对GP2,齿轮对GP1 和齿轮对GP2 之间的齿比差异决定了结合操纵元件A 和操纵元件B 在子机构F1和子机构F4之间传动比的差异。同理可推,与电机固连的输入构件到与输出端相连的输出构件间的传动比,就是该模式下驱动系统的传动比。
建立如图4 所示的功能分析图论模型:子机构用点表示,连接两个子机构操纵元件的状态用线表示。该图论模型包含的点的个数模型等于子机构个数,图4 中的各个元素在图1 中都有相对应的部分,如图4中点1和点2分别表示图1中的子机构F1和子机构F2,作为输入端分别与电机EM1 和电机EM2 相连接,点3 表示子机构F3,作为输出端与输出轴相连接,点4 表示子机构F4。模型中线表示不同子机构之间的动力传递路径,每条线表示一类路径,并非特指一条路径。因此该功能分析图论模型可称为以子机构为基本单元的运动拓扑图论模型。
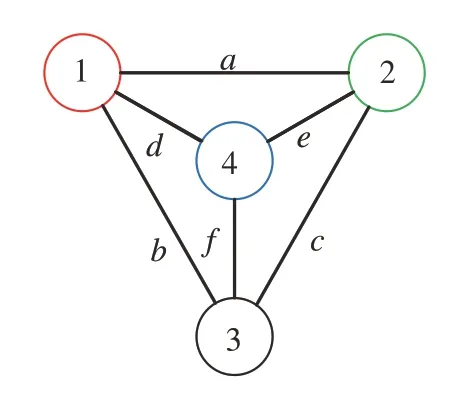
图4 功能分析图论模型
2.2 可耦合路径约束条件
双电机耦合驱动系统中两电机可同时工作,需要多条路径耦合共同传递动力。路径耦合应当遵守不干涉原则,即耦合路径构成的图论模型无回路,回路包含多点间形成的回路和两点间的子路径不同而形成的回路两种类型,如图5所示。

图5 多路径运动干涉
多点间形成的回路:电机EM1 的动力传递路线对应的图论模型中路径为1-a-2-e-4-f-3,如图5(a)所示。电机EM2 的动力传递路线对应的图论模型中路径为2-c-3,如图5(b)所示,则两条路径同时存在时会产生回路2-e-4-f-3-c-2,如图5(c)所示。两点间的子路径不同而形成的回路:电机EM1 的动力传递路线对应的图论模型中路径为1-a-2-c1-3,如图5(d)所示,电机EM2 的动力传递路线对应的图论模型中路径为2-c2-3,如图5(e)所示,则两条路径同时存在时会产生回路2-c1-3-c2-2,如图5(f)所示。
经运动干涉筛选,可耦合路径如图6 所示。用箭头表示动力传递方向,其中红色箭头表示电机EM1 传递的动力,绿色箭头表示电机EM2 传递的动力,红色和绿色的复合箭头表示耦合后两个电机传递的路径。

图6 可耦合路径
2.3 功能生成过程
遍历路径叠加过程,经可耦合路径判别,获取所有可能存在的操纵序列,多数操纵序列虽然能够满足系统功能,但需求的子路径较多,本文以子路径的数量作为筛选条件,包含子路径最少的操纵序列作为优选操纵序列。筛选后可以得到9 种操纵序列,优选操纵序列及其子路径个数、种类如表1所示。
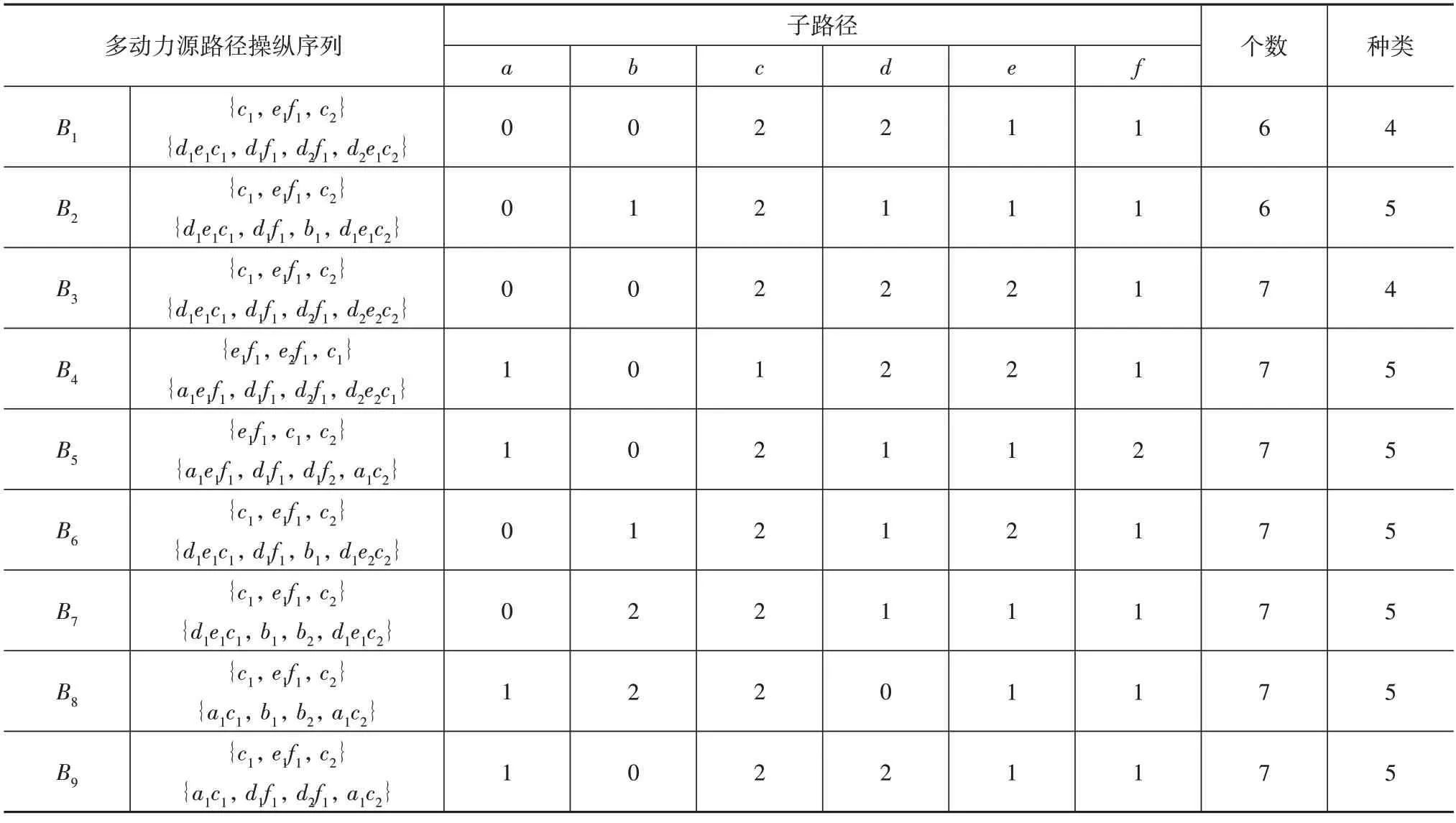
表1 多动力源路径操纵序列
3 基于功能需求的结构衍生
3.1 构型二级简化及衍生方法
两个子机构间的操纵元件位置既不会影响齿轮对、轴、套轴等结构,也不会影响机构自由度、操纵序列等功能需求。因此,可以将图7(a)所示的传动方案简化成图7(b)所示的形式,简化后的机构能反映齿轮、轴、套轴等构型特征,定义这类机构为齿轴构型,其中灰线定义为变连接结构,其一端与其他构件连接的齿轮或轴,另一端根据操纵元件状态决定连接与否。若忽略同属性变连接结构的数量,则齿轴构型可以简化成图7(c)所示机构,称之为基本构型。综上所述,基本构型就是不考虑同一属性变连接结构数量的齿轴构型。

图7 构型的二级简化((a)具体构型,(b)齿轴构型,(c)基本构型)
双电机耦合驱动系统构型经过齿轴构型和基本构型二级简化后,结构更加简单且构件数量明显减少。本文提出依次进行基本构型、齿轴构型、传动构型的结构衍生方法。首先根据子机构个数、子路径属性等功能需求,进行轴、套轴和固定连接结构的设计,获得基本构型。然后在基本构型的基础上依据各个子路径个数进行变连接结构添加,获得齿轴构型。最后在空间约束以及运动约束下寻求最优的操纵元件布置,获得满足功能生成的构型。具体流程如图8所示。
3.2 基本构型
基本构型是由轴、套轴、固定连接结构以及与不同属性的变连接结构组成。本文以同轴对置双电机为例,首先确定理论存在的布置形式,筛选出能添加与操纵序列对应的所有属性的变连接结构的固定连接机构,将各属性的变连接结构添加至由轴、套轴和固定连接结构组成的机构中形成基本构型。
以序列B1为例,对其结构进行分析。序列B1包含的子路径、其连接的自由度及个数如表2 所示,固定连接结构和基本构型分别如图9(a)和图9(b)所示。
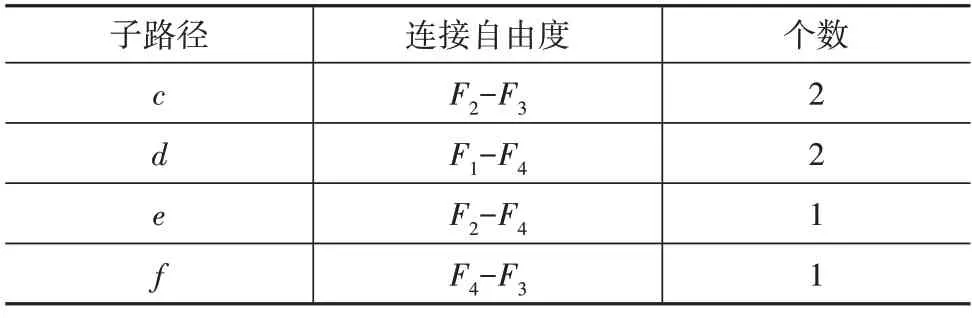
表2 序列B1包含的子路径

图9 操纵序列B1的结构衍生过程
3.3 齿轴构型
依据各属性变连接结构的个数在基本构型上进行齿轴构型衍生。除去两个输入轴以外,位于同一轴系中两个顶轴或轴与套轴之间形成的,无须经过齿轮对的变连接结构定义为附加变连接。根据操纵序列中各属性子路径个数增加基本构型中相应的变连接结构进行齿轴构型的衍生。齿轴构型衍生需要的变连接结构数量ni_SGS为
式中:ni_SP为操纵序列中子路径i的数量;ni_AVC为基本构型中子路径为i的附加变连接结构的数量。如果ni_SGS≤0,说明齿轴构型衍生不需要子路径i的变连接结构。
通过变连接结构和固定连接结构的数量可以计算齿轴构型中齿轮对的数量nGP:
式中nPC为基本构型中固定连接结构数量。
两个输入都布置在第一轴系,且位于两侧。由于传动机构具有4 个子机构,两个输入轴(套轴)分别属于两个子机构,输出轴属于一个子机构,另一个子机构包含的轴或套轴既可以位于第一轴系也可以位于第二轴系。在轴与输入输出布置的基础上增加固定连接结构,使机构能形成4 种类型的变连接结构(b,d,e,f),例如在输入输出布置形式中,存在子机构F2与F3之间的变连接结构e,因此机构F2与F3应处于不同轴系中,以齿轮对的数量为条件,筛选出每个序列所需齿轮对最少的基本构型,在此基础上,根据变连接结构的数量推出齿轴构型,其中B1的结构衍生过程如图9所示。
3.4 操纵元件布置
操纵元件同步器具有左啮合、右啮合和不啮合3 种状态,状态及空间上均存在约束关系。因此,须针对优选齿轴构型进行同步器布置设计。同步器布置须满足4个约束:
(1)同一同步器左啮合和右啮合对应的变连接结构不能同时出现在耦合路径所包含的变连接结构中。在实际工作中,同步器的左啮合和右啮合不存在同时结合的情况,若分别在相邻挡位或耦合模式下结合则无法进行动力换挡。
(2)两个同步器不能布置于两轴系的同一纵向位置。根据工程经验,同步器直径往往大于传动机构的中心距,因此无法布置于两轴系的同一纵向位置。
(3)最大限度的成对布置。为采用最少数量的同步器实现操纵序列需求的变连接结构,每个同步器应尽可能包含两个变连接结构。
(4)同步器尽量置于第一轴系中。为便于执行机构设计,本文所设计的同步器优先布置于第一轴系。
根据操纵序列相邻挡位关系获得可布置于同一同步器的变连接结构,再根据齿轴构型中变连接结构的空间约束进行筛选,确定同步器个数、存在的状态以及各状态处于的变连接结构,获得优选传动机构。
以操纵序列B1为例,其形成的传动机构中均由4个同步器构成,有两种布置形式:c1-c2,d1-d2,e1,f1和c1-d2,c2-d1,e1,f1。在B1所对应的齿轴构型中,变连接结构c和d无法由同一同步器的两个位置形成。因此,同步器的布置形式只能为c1-c2,d1-d2,e1,f1。类似地可以得出所有优选序列同步器的布置形式。各个变连接相邻挡位的变连接结构、可成对布置的变连接结构关系以及同步器合理布置形式如表3所示。
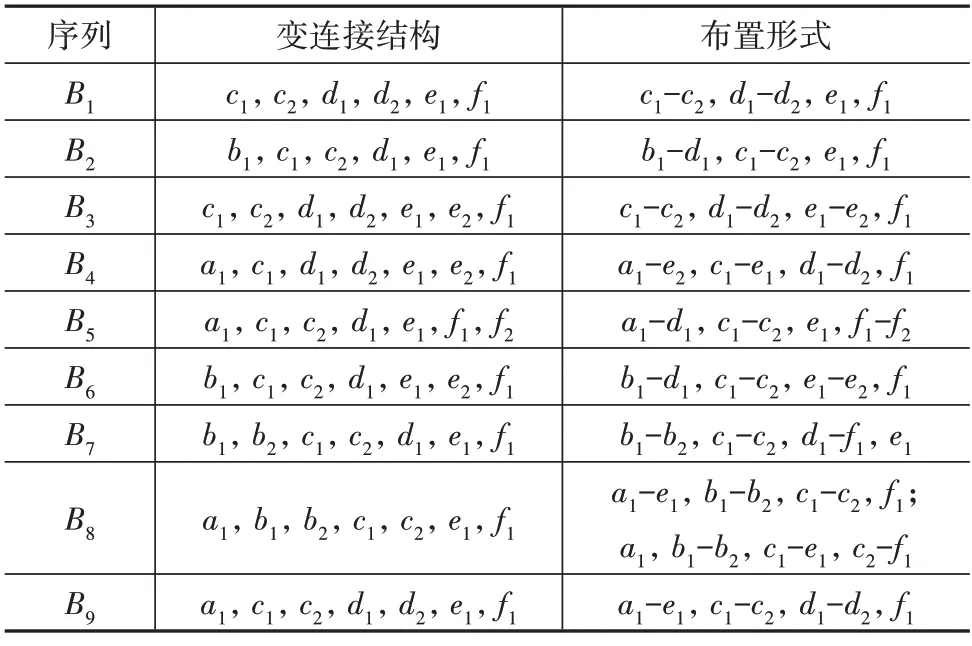
表3 变连接结构属性及其布置形式
根据各个序列的同步器布置形式,按照布置原则,在齿轴构型的基础上添加同步器,优选双电机耦合驱动系统构型如图10所示。

图10 优选双电机耦合驱动系统构型
4 参数匹配与经济性分析
4.1 参数匹配
纯电动商用车原车参数如表4 所示。驱动系统参数如表5 所示。原电机MAP 如图11 所示。为检验双电机耦合驱动系统优势,选取功率和与原单电机相同的双电机,峰值功率均为130 kW,峰值转矩均为1 400 N·m,电机EM1 和EM2 的峰值转速分别为3 000 和4 500 r/min。

表5 原车驱动系统参数
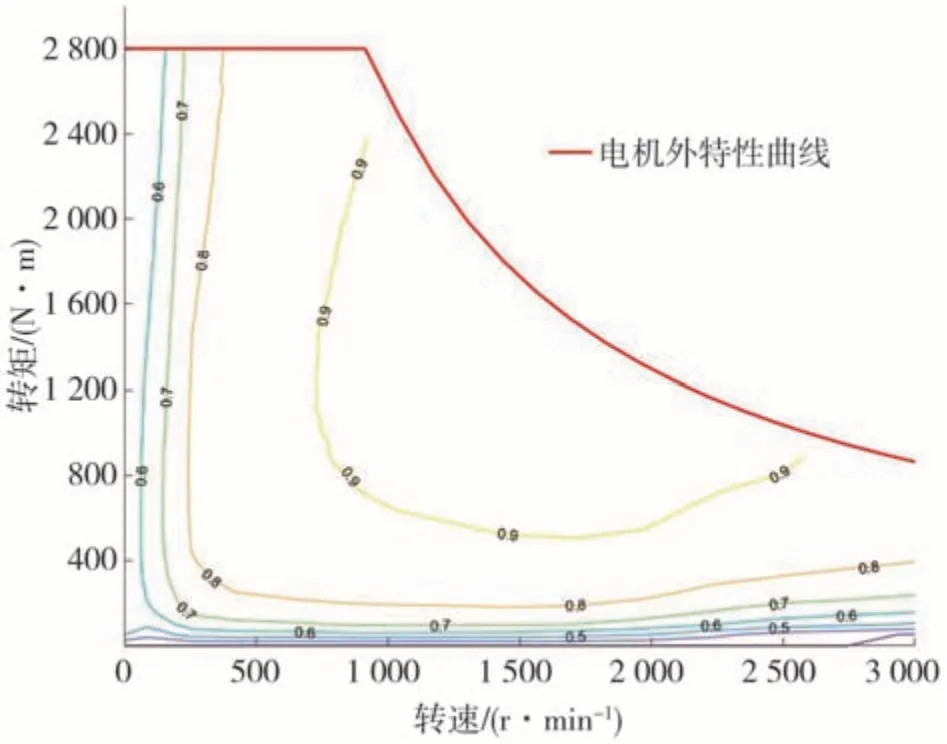
图11 驱动电机MAP图
考虑最大爬坡度、附着率以及汽车最低稳定车速确定最大传动比,最大传动比和最小传动比与整车参数和电机参数分别满足式(3)和式(4)。
式中:imax为最大传动比;imin为最小传动比;G为车辆所受重力;f为滚动阻力系数;αmax为最大爬坡度;r为轮胎半径;Ttqmax为双电机峰值转矩之和;ηT为传动效率;nmax为电机峰值转速;umax为最高车速。
由于双电机耦合驱动系统中电机EM1 和EM2的最大转矩均为1 400 N·m,所以两个电机所对应的两组传动比的最大传动比相同,即i1max=i2max≥15,最小传动比分别为:i1min≤5.79,i2min≤8.65。
传动比设计应遵循随挡位数的增加变速器的阶比逐步减小的原则,并采用修正等比级数进行各挡的理想速比设计。定义R1,R2,R3,…,Rn为第1,2,3,…,n挡的传动比,n速双电机耦合传动机构的传动比可以由式(5)得到[20]。
根据式(5),取参数ax为0.6,得到参数r以及各挡Ri的传动比均可以计算获得,结果如表6 所示,其中EM1 对应的R1~R4表示电机EM1 驱动的4 个挡位传动比,EM2 对应的R1~R3表示电机EM2 驱动的3个挡位传动比。

表6 驱动系统理论传动比设计
4.2 经济性分析
采用瞬时最优能量管理策略,对双电机耦合驱动系统进行经济性分析。C-WTVC 循环工况下的车速-时间曲线和需求功率-时间曲线分别如图12 和图13所示。
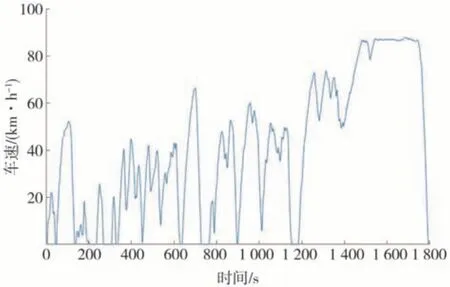
图12 C-WTVC循环工况下车速-时间曲线
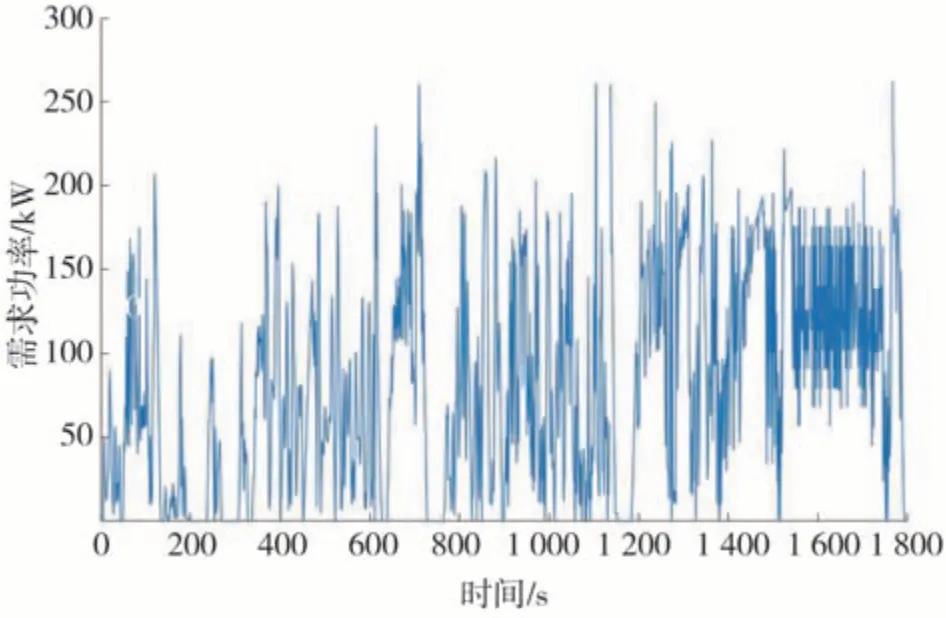
图13 需求功率-时间曲线
驱动系统模式与双电机传递路线的分配如表7所示。总共包括9 种模式,在循环工况下的模式-时间曲线如图14 所示。单电机驱动系统的电机工作点分布如图15 所示。双电机耦合驱动系统电机EM1 和电机EM2 的工作点分布分别如图16 和图17所示。通过对比分析两个驱动系统的电机工作点可以确定,相较于单电机驱动系统,双电机耦合驱动系统两个电机的工作点更多分布在高效范围。

表7 驱动系统模式与双电机工作挡位分配

图14 驱动系统模式-时间曲线

图15 单电机驱动系统电机工作点
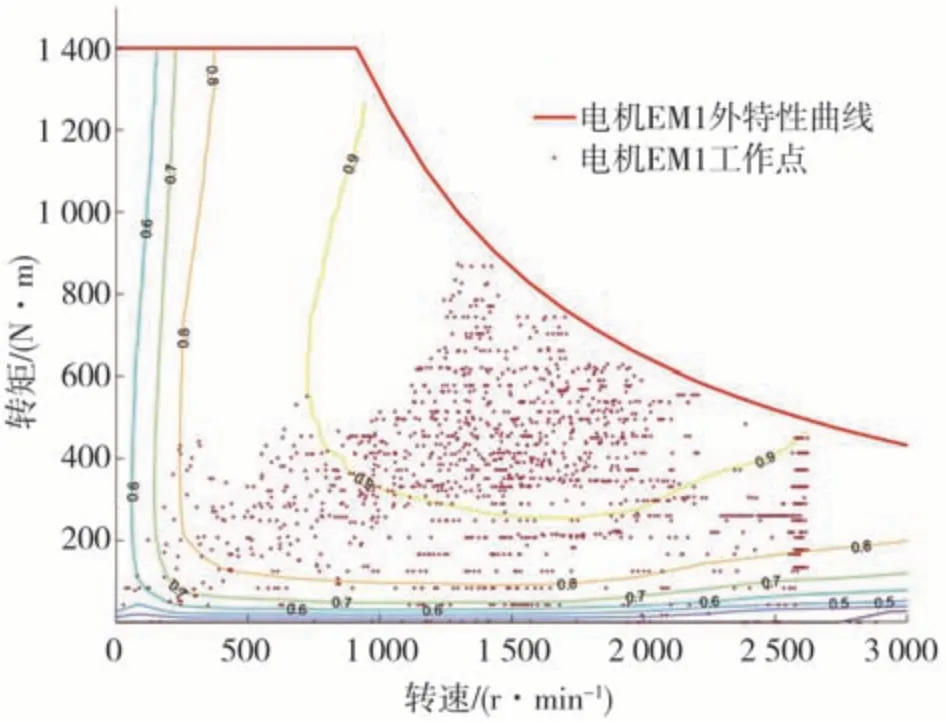
图16 双电机耦合驱动系统电机EM1工作点
单电机驱动系统和双电机耦合驱动系统在CWTVC 工况下的电池SOC 变化情况如图18 所示。明显可见,双电机耦合驱动系统的电池SOC 一直高于原单电机驱动系统,原单电机驱动系统的百公里能耗为108.112 kW·h,双电机耦合驱动系统的百公里能耗为98.415 kW·h,能耗降低了8.97%。可见双电机耦合驱动系统可以有效减小整车的电能损耗,提高车辆在C-WTVC循环工况下的整车经济性。
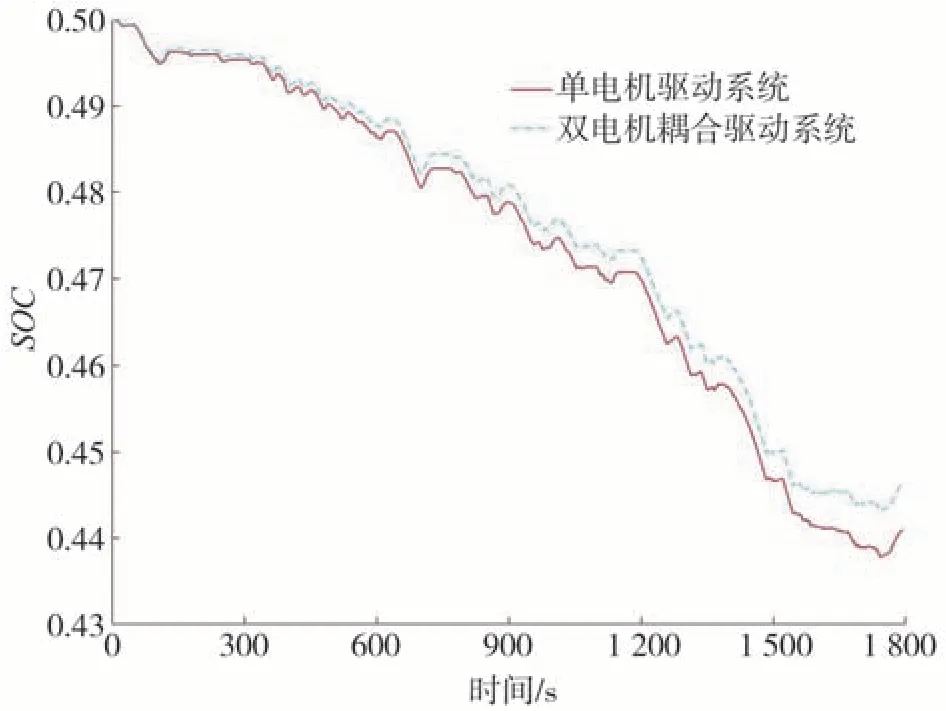
图18 两种驱动系统的SOC
0—50 km/h的加速度-时间曲线和速度-时间曲线如图19 和图20 所示。其中虚线表示双电机耦合驱动系统,实线表示原车单电机驱动系统。双电机耦合驱动系统在换挡过程中动力不中断,换挡冲击小。加速时间缩短了8.9 s,由此可见双电机耦合驱动系统的动力性相较于原单电机驱动系统有明显提升。

图19 两种驱动系统加速度-时间曲线
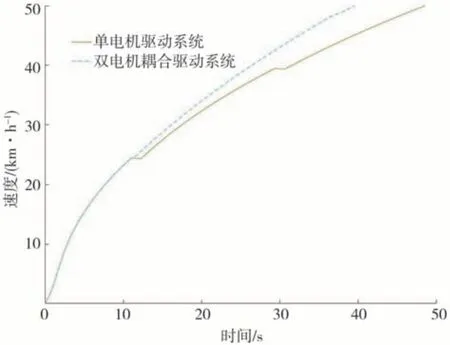
图20 两种驱动系统速度-时间曲线
5 结论
以实现无动力中断换挡功能为前提,提出了一种双电机耦合驱动系统设计方法,为进一步优化商用车辆的驱动电机工作区间,提供新的理论和技术参考。
采用功能分析法,对车辆进行功能需求分析,匹配出3+4 型双电机耦合驱动系统,建立以子机构为基本单元的图论模型,搜索得到9 种多动力源操纵序列作为功能生成路径。
基于功能需求,以基本构型、齿轴构型、传动方案的顺序逐级衍生,得到传动构型后,排除同构方案,优选出9种4+3型双电机耦合驱动系统构型作为功能生成载体。
参考某一纯电动商用车,基于优选构型进行参数匹配与经济性分析,在C-WTVC工况下,采用双电机耦合驱动系统的百公里能耗为98.415 kW·h,相比目标车辆原采用的单电机驱动系统108.112 kW·h的能耗,降低了8.97%。
