面向量产的自适应巡航控制系统纵向加速度规划方法研究

芦 勇，何一超，田 贺，江 昆，杨殿阁

（1.清华大学车辆与运载学院，北京 100084；2.联创汽车电子有限公司，上海 201206）

前言

近几年，我国乘用车智能驾驶辅助系统的渗透率逐年提高，L2 级系统为增长的绝对主力。当前10-20 万元价位车型占国内乘用车市场的50%以上，是大多数消费者优先考虑的购车价位。考虑到智能驾驶辅助系统的应用成本，该价位段的视觉产品形态主要为单摄像头或单摄像头与毫米波雷达的组合，规划控制算法主要在低算力的MCU 上运行。在有限的硬件资源下，采用何种加速度规划方法是实现自适应巡航控制（ACC）系统量产开发的关键问题。

ACC系统包含定速巡航和跟车控制。定速巡航加速度规划较为简单，通常采用比例反馈的规划策略，包括优化期望加速度的PID 参数等，但由于PID的参数标定需要丰富的工程经验，不适配多车型多时距配置的量产巡航车速控制。此外，模糊逻辑控制因其灵活易实现的特点，是巡航期望加速度优化的另一重要方向［1］，但其缺点是需要调节较多参数，较难应用于工程实践。而基于自适应动态滑模的巡航控制方法［2］虽可消除参数不确定性和外部干扰等因素，但其上层巡航加速度规划采用“2-1-2 样条线”平滑计算方法，并没有考虑加速度变化率的影响，不能保证在任意工况下期望加速度的平顺性。所以，降低调参难度，提升多车型多时距适配性和舒适性是定速巡航规划方法实现量产的主要任务。

跟车加速度规划最早在交通领域研究跟车模型时涉及，Brackstone 等［3］梳理了5 类跟车模型：Gazis-Herman-Rothery 模型、避碰模型、线性模型、心理模型及模糊逻辑模型。除了跟车模型，学者从其他维度阐述了多类ACC 期望加速度的规划方法，最为常见的是线性最优二次型调节器［4］、模糊逻辑［5-6］、模型预测控制（MPC）［7-10］、强化学习［11-12］及人工神经网络［13-14］等。线性最优二次型调节器最优控制率的最终表现形式与PID控制是一致的，通过两个独立的P控制修正距离误差和相对速度误差［15］，但该方法的缺点是无法引入优化的概念，调参的结果往往难以实现各目标的均衡。Tsai 等［6］提出了两输入单输出的模糊逻辑规划策略，输入为距离误差和速度误差（其中距离误差中预留了安全距离），输出为加速踏板或制动踏板的开度。试验结果表明，该模糊逻辑控制器在满足舒适与安全的前提下，在高速和低速工况下都能取得满意的性能。虽然模糊逻辑可以很好地模仿人的推理行为，对非线性系统、混杂系统无须建立准确的模型，但是其缺点在于容易产生无优化的结果，除此之外策略需要调节的参数较多，给工程实现带来一定困难。Li等［10］提出了基于多目标优化的ACC 分层控制策略，MPC 上层规划中代价函数为二次多项式，考虑跟踪误差、油耗及驾驶员的动态跟随特性，而纵向跟车舒适性、跟踪距离范围以及安全性则使用线性约束表达。其MPC 求解采用二次规划算法，并使用软约束避免计算不可行。仿真结果表明，该ACC 系统在燃油经济性和跟踪能力方面具有显著的优势，同时也满足了驾驶员期望的跟随特性。但未经算法优化的MPC 计算耗时长，资源占用较大［16］，且对模型的准确性要求较高，故难以在低算力控制器上实现量产。Zhao 等［11］提出了一种有监督的基于强化学习的ACC 期望加速度规划方法，对ACC 的近似最优控制策略进行学习，多个场景的试验结果表明该方法能够取得良好的性能，但当测试输入超出训练样本范围时，深度强化学习的性能会弱化，表明其泛化能力不足，无法保证量产所需的高安全和高可靠性。David 等［13］考虑车辆制动过程中的影响因素，在制动减速度规划方法中采用3 层人工神经网络训练得出期望减速度，提高车辆安全性，但此方法没有考虑制动过程中舒适性影响因素，且神经网络需要大量数据进行训练，对多场景多工况的数据采集有较高要求，多车型适配的数据采集和训练成本也较高，不适合量产。对比上述跟车加速度规划方法，He 等［17］具体分析了PID 控制、MPC控制和模糊逻辑控制的优缺点。其中，由于MPC 考虑了系统未来状态信息，规划得到的期望加速度能实现更好的舒适性和安全性，具备量产ACC 系统所需的高安全和高可靠性，但运行MPC 算法所需的高算力要求又无法实现基于低成本视觉和硬件方案的ACC 系统量产。同时，MPC 中的预测时域无法根据多场景进行自适应调整，难以支撑多车型量产。因此，如何优化MPC 算法是跟车加速度规划研究的关键。

针对上述问题，本研究提出一种面向量产的ACC系统纵向加速度规划方法。定速巡航规划采用多维优化PID 控制方法，借助PID 控制思想并降低调参难度，设计可适配多时距的二维加速度上下限表，提升多车型适配的高通用性。跟车巡航加速度规划采用基于动态预测时域的模型预测控制方法。分别设计了目标车加速度处理、执行器效率和延迟预测处理、动态时域管理、模型预测控制器、加速度变化率约束、多目标加速度规划决策等模块，用以满足高安全、高可靠、低资源占用的量产要求。系统通过并行巡航期望加速度规划和跟车期望加速度规划，决策两者规划结果得到待输入给下层执行器控制的最终期望加速度。最后进行多款量产车辆道路试验，通过分析试验结果验证该规划方法的效能。

1 定速巡航期望加速度规划

对于定速巡航加速度规划，本文提出了如图1所示的多维优化PID 控制方法，包括多维加速度查表计算和加速度变化率约束。为适配多时距设置时的加速度规划差异性，多维加速度查表计算借助PID 控制思想，合理划分输入端的误差段和时距段，离线设计2 输入1 输出的二维加速度上下限表aup(Δe，tdsr)和alo(Δe，tdsr)。其中，输入端为巡航车速误差输入量Δe和驾驶员设置时距tdsr，Δe的表达式如式（1）所示。

式中：Δe表示巡航车速误差输入量；vset表示巡航设定车速；vh表示自车车速。故无加速度变化率约束条件下的定速巡航期望加速度计算表达式为

式中：aup(Δe，tdsr)和alo(Δe，tdsr)分别表示离线设计的二维加速度上下限表；afnl(k-1)表示综合跟车期望加速度决策后的上一时刻最终期望加速度，具体决策过程可参见式（54）。

为了满足法规对纵向加速度变化率要求和保证车辆行驶舒适性，需要对进行必要的加速度变化率约束，此刻的加速度变化率限制量记为jc(k)。针对不同车型项目，结合智能判断驾驶员改变巡航车速快慢的意愿和驾驶员加速踏板操控结束后的巡航舒适性原则，灵活设置加速度变化率限制值，继而计算得到自车的定速巡航期望加速度，其计算表达式如式（3）所示。

式中：jc(k)表示加速度变化率限制量；T表示单个时间步长。

2 跟车巡航期望加速度规划

本研究采用的跟车巡航加速度规划框架如图2所示，包括目标车加速度处理、执行器效率和延迟预测处理、动态时域管理、模型预测控制器、加速度变化率约束、多目标加速度规划决策等组成部分。首先，由目标级感知得到多目标的距离、速度和加速度信息，经过目标车加速度处理，修正和补偿单一传感器识别的不精确目标加速度。其次，考虑执行器效率和响应延迟时间，预测自车与目标车相对运动状态。再次，通过动态时域管理，自适应多场景多工况下的MPC 预测时域，并简化目标函数求解复杂度，得到单跟车目标期望加速度。最后，通过加速度变化率约束和多目标加速度规划决策得到多目标跟车期望加速度。综合定速巡航加速度规划和多目标跟车加速度规划，由自适应巡航加速度规划决策得出最终期望加速度。

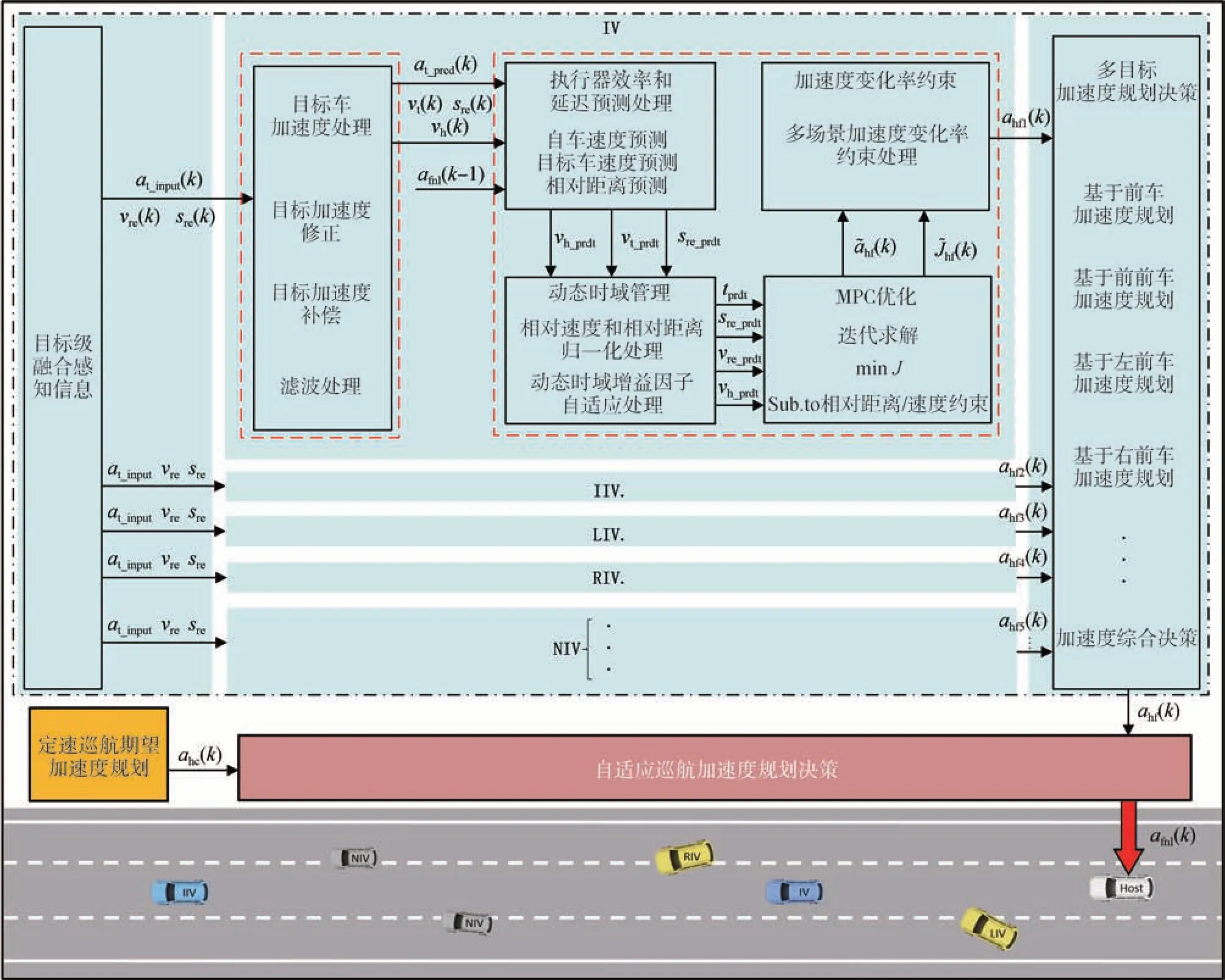
图2 跟车巡航加速度规划框架

2.1 目标车加速度处理

目标车加速度处理模块逻辑框图如图3 所示，包括目标加速度修正、目标加速度补偿和目标加速度滤波。目标车加速度感知输入经积分处理得到目标车估算速度vt_est(k)。其中，积分的初始化条件为无目标车或目标车ID 切换，初始化值为目标车感知速度vt。目标车估算速度与感知精确的目标车速度作差得到速度误差，通过比例运算进一步得到目标车加速度估算误差at_err(k)。用此误差修正目标车加速度感知输入值at_input(k)，得到未经滤波的目标车加速度修正值at_unflt(k)，继续参与下一积分循环运算。而后经1 阶滤波运算得到最终目标车加速度修正值at_mfd(k)。上述修正过程可由式（4）～式（8）表示，其中离散积分运算采用前向欧拉法。

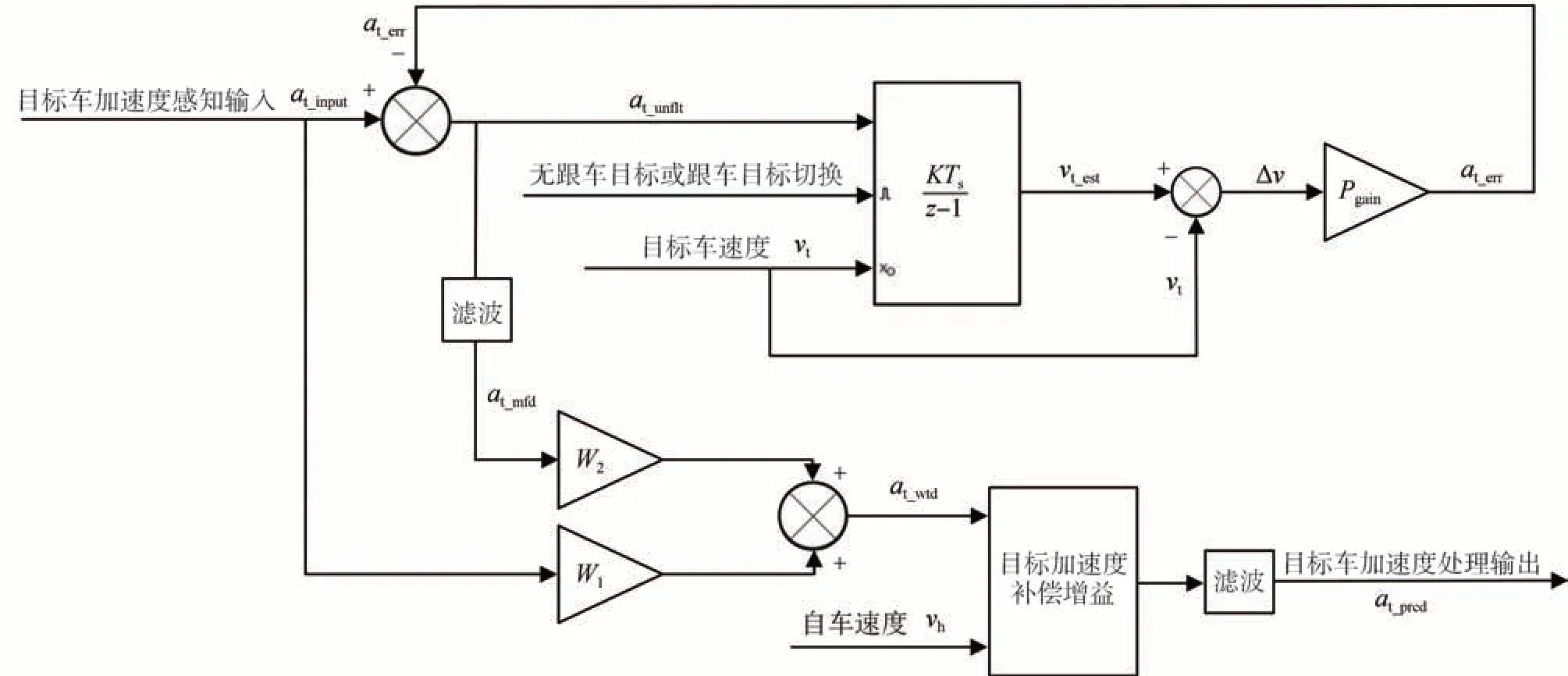
图3 目标车加速度处理

式中：vt_est(k)为目标车估算速度；at_err(k)、at_input(k)、at_unflt(k)、at_mfd(k)分别为目标车加速度估算误差、目标车加速度感知输入、未经滤波的目标车加速度修正值和最终目标车加速度修正值；kflt为滤波系数。

由目标加速度修正环节得到的加速度修正值与目标车加速度感知输入值进行变权重求和处理。依据车型不同、场景不同设置不同的权重，将对应的权重与目标加速度修正值与目标加速度感知输入值进行相乘后求和。其计算过程可由式（9）表示。

式中w1和w2为权重系数。

为应对目标车大减速等极端场景，需要对目标车加速度进行适当的增益补偿，提高跟车的行驶安全性。目标车变权重后的加速度值和自车速度作为二维信息输入进行增益补偿处理，根据车型参数和感知方案所识别目标车加速度精度的差异性进行增益值调节，以适配指定量产车型和传感器方案。为消除加速度增益补偿环节所引起的加速度波动，须进行必要的限幅和滤波处理用以平滑目标车加速度计算值，得到后续跟车加速度规划处理模块所需的目标加速度值at_prcd(k)。目标加速度补偿和滤波的计算过程可由式（10）和式（11）表示。

式中：alo、aup分别为加速度上、下限；p(at_wtd(k)，vh(k))为二维增益补偿系数为滤波系数。

2.2 执行器效率和延迟预测处理

由于车辆的驱动制动执行器存在响应延迟和响应误差，本文在目标加速度处理后加入了执行器效率和延迟预测处理环节，预测延迟响应后的自车与目标车相对运动状态，可更精确地进行跟车加速度规划，提升系统安全性。执行器响应的稳态误差反映了自车期望加速度的执行效率，而驱动制动的执行效率往往不同，由ebrk和eacceltn进行表征，进而估算出车辆实际执行的期望加速度ahfe(k)，并可由式（12）表示。

通过估计自车驱动制动执行器的延迟周期，预测自车和目标车速度以及自车和目标车的相对距离。预测过程可由式（13）、式（14）和式（15）表示。

式中：N表示执行器的延迟周期；vh_prdt(k)为自车的预测速度；vt_prdt(k)为目标车的预测速度；sre(k)为自车和目标车的感知距离；sre_prdt(k)为自车和目标车的相对预测距离。

2.3 动态时域管理

继执行器效率和时延预测处理后，须进行跟车期望加速度计算。为了提高车辆行驶安全性和舒适性，提升系统动态控制性能，强化抗扰动等能力，采用了滚动优化策略的模型预测控制方法来获得期望加速度。针对多场景多工况下车辆加速度规划预测时长问题，模型预测控制的预测时域由动态时域管理模块进行处理。采用动态实时调节策略，根据自车和目标车相对运动状态划分为相对距离和相对速度两个维度设计动态预测时域，可使模型由畸变或扰动等引起的不确定性得到弥补，优化其控制性能。

动态时域管理由相对速度、相对距离归一化处理和动态时域增益因子自适应处理组成。相对速度和相对距离归一化处理将自车和目标车相对运动状态划分为速度和距离两个维度，可更合理地设计动态时域增益因子，进而获得适应性高的预测时域。其归一化处理过程可由式（16）和式（17）表示。

式中：vt_prdt(k)表示目标车预测速度；vh_prdt(k)表示自车预测速度；sre_prdt(k)表示自车与目标车相对预测距离；sd(k)表示不同设定时距下的自车与目标车期望距离；Rvr(k)为相对速度归一化表示；Rsr(k)为相对距离归一化表示。

由相对速度和相对距离两个维度的归一化确定动态时域增益因子tg1(k)。由Rvr(k)和Rsr(k)分别代替x轴和y轴，可将二维空间划分为4个象限：第1象限代表自车与目标车的相对速度大于零且相对距离大于设定时距下的期望距离；第2 象限代表自车与目标车的相对速度小于零且相对距离大于设定时距下的期望距离；第3 象限代表自车与目标车的相对速度小于零且相对距离小于设定时距下的期望距离；第4 象限代表自车与目标车的相对速度大于零且相对距离小于设定时距下的期望距离。不同象限下可根据具体车型对跟车性能的要求设计由式（18）表示的动态时域增益因子tg1(k)，其参数设计规律为：可在第1 象限设置较大值，增大预测时间提高舒适性；在第3 象限设置较小值，在应对紧急工况时减少预测时间提高安全性；在第2和第4象限可设置介于第1和第3象限的参数值。

为了降低动态时域增益因子tg1(k)适配不同车型的标定工作量，设计了另一个动态时域增益因子tg2(k)，其表达式可由式（19）表示，并作为关于自车预测速度的函数。针对不同车型，可在基本不改变动态时域增益因子tg1(k)的情况下，设计不同速度段的增益因子tg2(k)以适配全场景跟车要求。这不仅大幅降低预测时域因子的标定难度而且进一步提高车型自适应能力，体现了系统的高通用性。结合动态时域增益因子tg1(k)和动态时域增益因子tg2(k)，总动态时域增益因子tg(k)可由式（20）表示。

由Rvr(k)和Rsr(k)所划分的xy二维坐标系，其上任一点距原点的距离可由式（21）表示。进一步地，动态预测时域的自适应计算由式（22）表征。由动态时域管理的计算过程可知，通过自车与目标车预测的相对运动状态可自适应调整预测时域长度，增强系统纵向规划控制的鲁棒性和车型自适应能力。

2.4 模型预测控制器

假设在动态预测时域内，其自车的期望加速度变化率是恒定的，则自车的运动学方程可由下列关系式表示：

运动学方程的约束条件如下：

式中：tprdt表示预测时域；jhf表示预测时域内恒定的加速度变化率；a0、v0、s0分别表示起始时刻自车加速度、速度和距离；st(tprdt)表示预测时域内目标车行驶距离和起始时刻感知距离之和；sd(vt(tprdt))表示自车期望的跟车距离。

将式（23）～式（26）表示的运动学方程转化为模型预测控制的离散时间状态空间模型，其状态方程和输出方程表达式为

其中：

状态矩阵、输入矩阵和输出矩阵分别为

由此可推得输出变量序列表达式：

式中：Np(k)表示k时刻预测时域周期数；Nc(k)表示k时刻控制时域周期数。

自车运动状态在预测时间终态须满足驾驶员设定的时距要求，即满足表达式（29）和式（30），约束条件满足式（27）和式（28）。为了降低模型预测控制的计算耗时，满足本研究面向的低算力硬件系统方案，设计代价函数如下：

其中：

求代价函数（36）最小值，即求：

进一步可推出：

其中：

故而可推得期望加速度为

由于两次滚动优化间计算的jhf(k|k)与jhf(k+1|k+1)往往不相同，两者的过渡存在较大的跳变不符合车辆的实际行驶状态，所以需要对式（39）中计算的加速度变化率jhf(k)进行优化，优化后的表达式为

式中cj为权重因子。

为进一步提高跟车安全性，在预测时域内划分16 个时刻，即1/16·Np(k)T，2/16·Np(k)T，…，16/16·Np(k)T，根据式（36）分别计算这16个时刻终态的代价函数，取其中计算所得最小的期望加速度。

特别地，由于状态空间方程未保证自车速度在预测时域内始终大于零，所以在预测时域内存在自车速度为负值情况时，即加速度为零时的速度极值小于零时刻，需要对终态条件进行修正，即

根据上述修正约束调整代价函数中的rs，可求得此特殊工况下的加速度变化率和期望加速度：

2.5 加速度变化率约束

为适应多场景下的车辆控制平顺性，须对特殊场景下的加速度变化率进行优化。对于前车切入场景，采用一种模糊逻辑校正策略［18］以提高该场景的制动平顺性，故优化后的加速度变化率如式（51）所示。

式中fj(k)为经模糊逻辑校正策略输出的加速度变化率修正系数。由上式加速度变化率约束后的跟车期望加速度为

2.6 多目标加速度规划决策

上述跟车加速度规划可针对多目标跟车场景进行并行计算，即可对前车（IV）、前前车（IIV）、左前车（LIV）、右前车（RIV）以及其他非前车（NIV）等跟车目标并行规划。例如，当自车正在以IV 作为目标跟车时，此时LIV 快速切入（cut-in），在IV 目标没有替换的过渡阶段，需要仲裁两者并行计算得出的期望加速度大小，提前采取制动保证cut-in 工况时的安全。如识别到IIV 正在减速而IV 还正常行驶未减速时，可由跟随IIV计算得出的期望加速度提前使自车减速保证安全。因此，通过决策多个目标并行规划出的加速度大小，可得出自车期望的多目标跟车加速度。其计算表达式为

式中：ahf1(k)，ahf2(k)，…，ahfn(k)表示由跟车加速度规划方法并行计算得出的n个目标跟车期望加速度；ahf(k)表示多目标跟车期望加速度。

根据设定巡航车速和多目标运动状态，系统并行定速巡航加速度规划和跟车加速度规划，通过式（54）决策得出最终期望加速度。由此，ACC 系统可在巡航状态和多目标跟车状态间自适应切换。特别地，在无跟车目标时只进行定速巡航加速度规划可进一步降低资源消耗。

式中：ahf(k)为定速巡航期望加速度；ahf(k)为多目标跟车期望加速度；afnl(k)为最终期望加速度。

3 实车试验

3.1 试验平台

为验证本文提出的纵向加速度规划方法的效能，借助上汽（SAIC）AP31 车型和爱驰（AIWAYS）M891 车型进行实车试验。图4 显示了上层规划算法采用的核心标定参数aup(Δe，tdsr)、alo(Δe，tdsr)和tg1(k)。AP31下层控制器采用基于前馈的PID 算法，可精确请求车辆驱动转矩和制动减速度指令；M891下层控制器算法集成在BOSCH 的ESP 系统中，可直接响应上层规划算法得出的期望加速度。如图5 所示，SAIC AP31 采用由单摄像头模组和英飞凌TC234 MCU 组成的辅助驾驶控制器，AIWAYS M891采用摄像头与前向毫米波雷达和4 个角雷达的5R1V 融合的视觉方案辅助驾驶控制器，其MCU为英飞凌TC397，将ACC 系统算法代码分别运行在上述两款车型的MCU 中。试验车辆经上海、四明山、淳安、黄山、宁国、广德、宣城、合肥、南京、常州、苏州，同时进行约1 万km 的道路测试，数据采集设备均使用VECTOR VX1000。

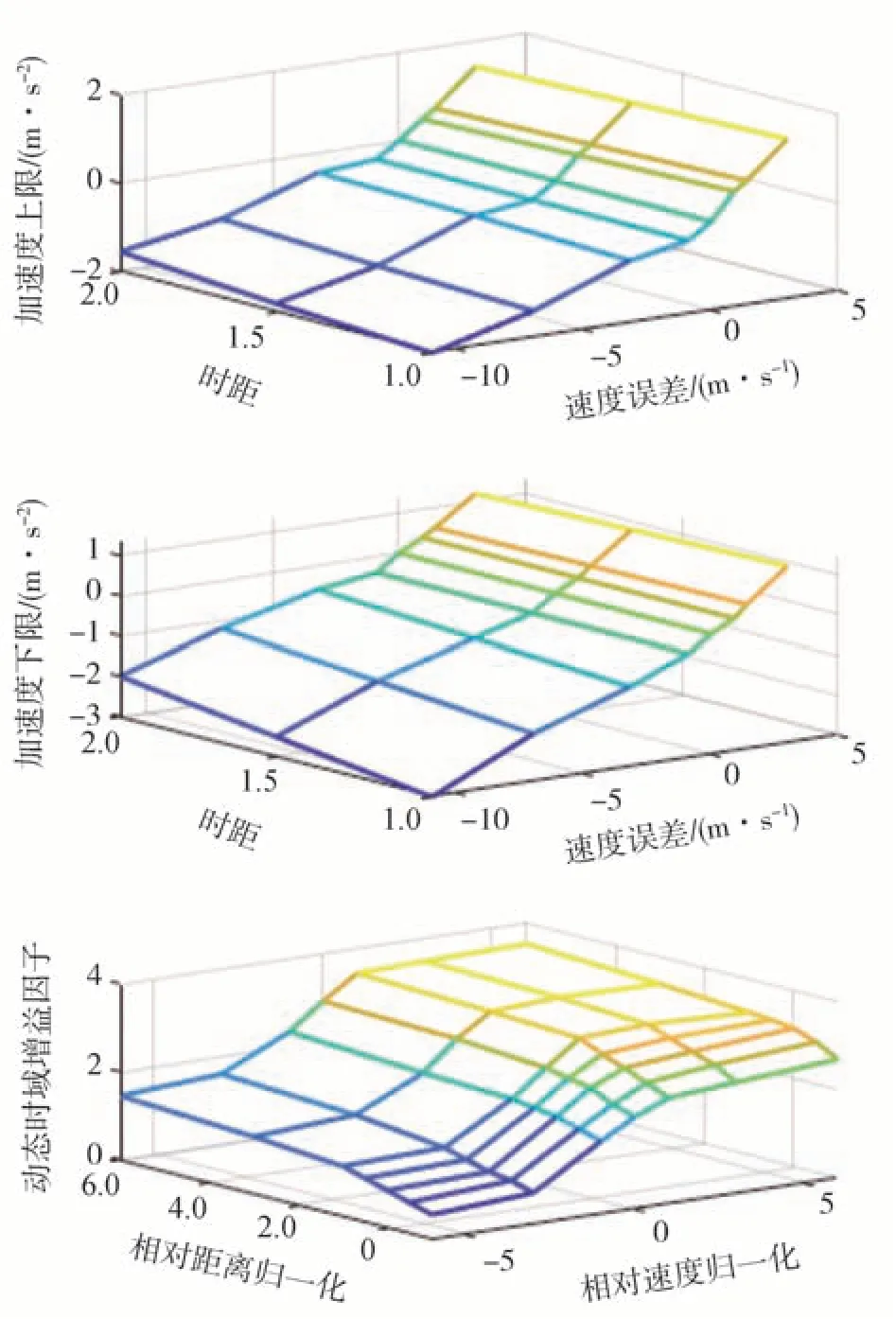
图4 加速度规划算法核心标定参数

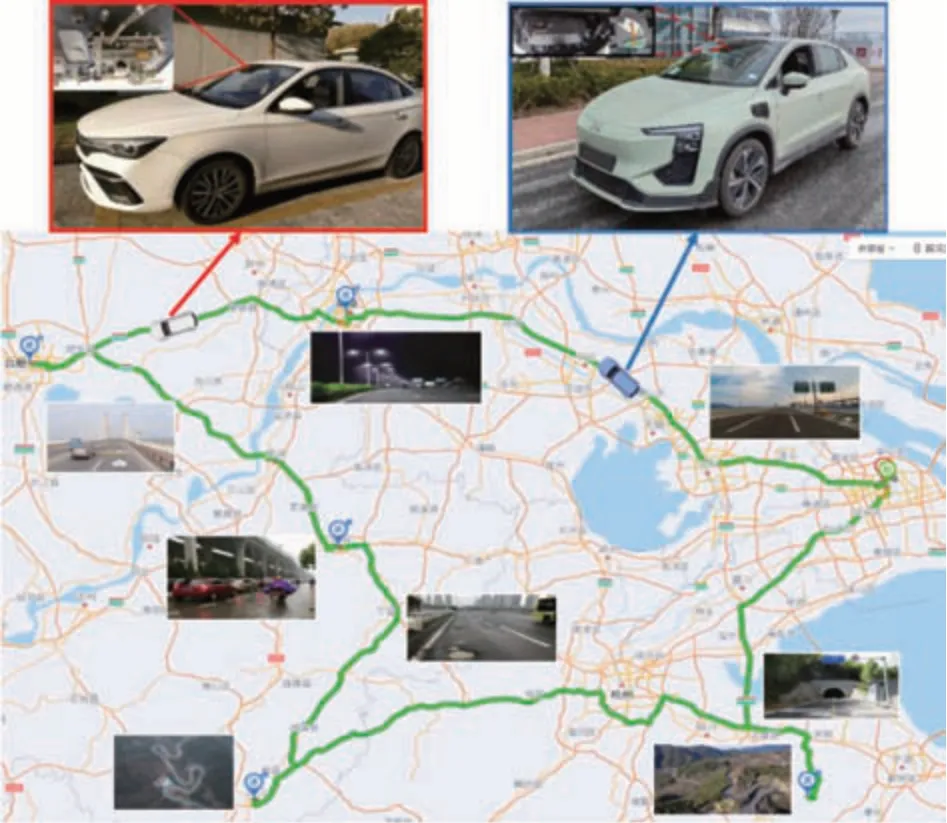
图5 量产车型试验平台和道路测试路线

3.2 试验结果和分析

从道路测试数据中选择SAIC AP31 和AIWAYS M891 的定速巡航、跟停静止前车和旁车切入（cutin）场景的试验数据进行量化分析，验证本文所提出纵向加速度规划方法的效能。同时，对两车1 万km鲁棒性测试结果进行数据统计，验证该纵向加速度规划方法是否满足舒适性和鲁棒性的量产要求。

图6 分别显示了AP31 和M891 在恒定巡航设定车速、增加巡航设定车速和减少巡航设定车速工况下的定速巡航测试结果。从测试结果分析，3 种工况下的期望加速度曲线均平滑，在实际车速和设定车速误差较大时，规划的加速度绝对值较大，车辆可通过快速加减速接近目标巡航车速；反之，值越小，车辆可避免控制超调，平稳达到设定车速。此外，仪表显示车速在稳态时均达到设定巡航车速值，误差小于±1 km/h。试验结果反映了本文所采用算法框架中的定速巡航规划方法可应对量产定速巡航各工况要求，有较强的车型适配能力和可靠性。

图6 定速巡航测试结果

图7 分别显示了AP31 和M891 在高速和中低速跟停静止前车的测试结果。分析测试结果可知，各速度段跟停过程期望加速度曲线都较为平顺。从速度和距离结果也反映出车辆运动状态较为线性；在跟停末段，车辆制动平顺，无二次起步或两段式制动现象，具有较高的行驶平顺性和乘坐舒适性。在识别静止前车时，系统可快速规划出较大的制动减速度，提高行驶安全性和驾驶员的乘坐信心，且由巡航状态转换至跟车状态时，期望加速度变化平稳，无跳变。特别地，高速跟停静止前车的测试结果反映了量产车辆可在80km/h 的速度下安全跟停前方目标车，具有较高的行驶安全性。测试结果表明，所提出的跟车巡航加速度规划方法在此典型场景下具有高安全性和高可靠性。

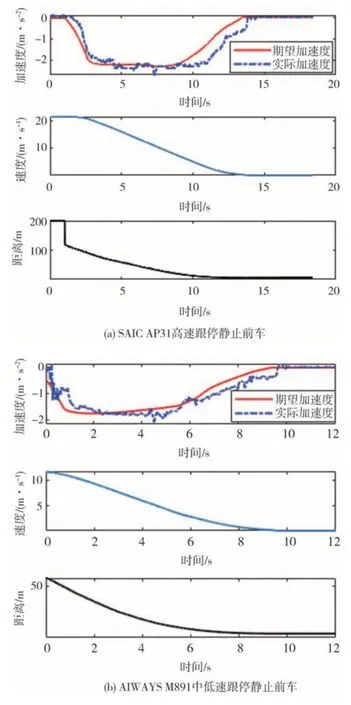
图7 跟停静止前车测试结果

图8 分别显示了AP31 和M891 在旁车近距离加速cut-in、旁车快速cut-in 后制动和多车连续cut-in工况下的跟车测试结果。图8（a）结果反映了在旁车近距离加速切入时，系统规划出的期望加速度绝对值较小，制动强度不大，符合人类驾驶习惯，具有较好的乘坐舒适性。由图8（b）旁车近距离切入后制动的测试结果可知，系统在cut-in 时迅速规划出较大的期望减速度，在1.5 s 左右前车采取制动后，又加大了期望减速度数值，保证车辆在应对该工况下的行驶安全性。图8（c）中多车连续切入的测试数据反映了系统在应对短时间内连续被cut-in 时的加速度规划能力，从整个时间维度来看，期望加速度曲线平滑，cut-in 时段的减速度规划合理，在保证安全性的前提下，提升了乘坐舒适性和行驶平顺性。测试结果还表明所提出的跟车巡航加速度规划方法在巡航跟车状态切换以及多目标跟车状态切换时加速度变化平稳，可满足多目标跟车场景的规划控制，具备多目标计算的可拓展性以及场景自适应性。

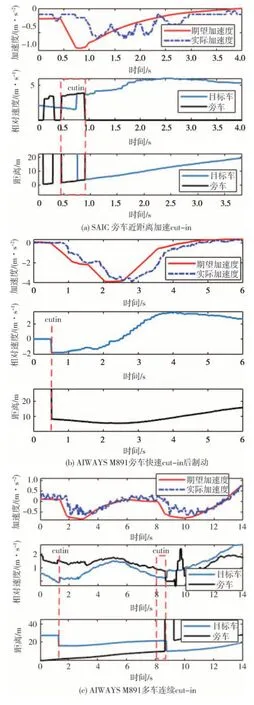
图8 cut-in测试结果

路试结果统计了AP31 和M891 在1 万km 鲁棒性道路测试中接管次数分别是86和74次，满足主机厂对于百公里接管次数小于1 次的安全性指标。同时，图9 和图10 分别显示了AP31 和M891 的1 万km路试舒适性统计结果。根据ISO 15622，ISO 22179和i-VISTA 关于ACC 加速度和加速度变化率的上下限规定，并结合主机厂主观评价，得出了加速度绝对值小于等于1 m/s2、加速度变化率绝对值小于等于0.5 m/s3时ACC 功能体感较好的舒适性评价经验。图9 的统计结果显示，AP31 车型的舒适体感加速度占比达到89.21%，小于等于0.5 m/s3的加速度变化率绝对值占比为91.86%。图10 的统计结果显示，M891 车型的舒适体感加速度占比达到86.95%，小于等于0.5 m/s3的加速度变化率绝对值占比为89.27%。从上述统计数据可知，本文提出的纵向加速度规划方法在适配的量产车型上具有鲁棒性和舒适性的显著特征。

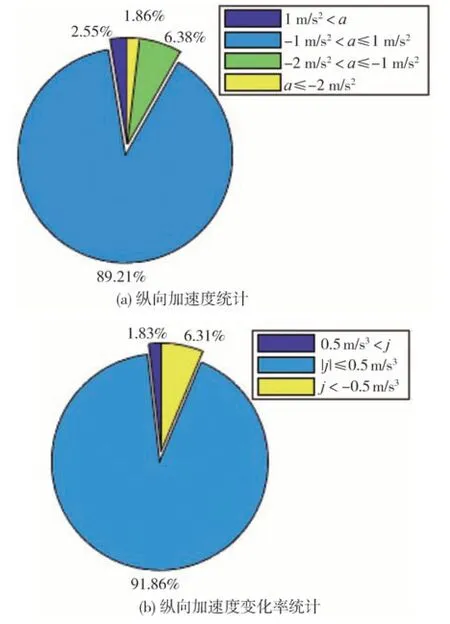
图9 AP31鲁棒性路试结果

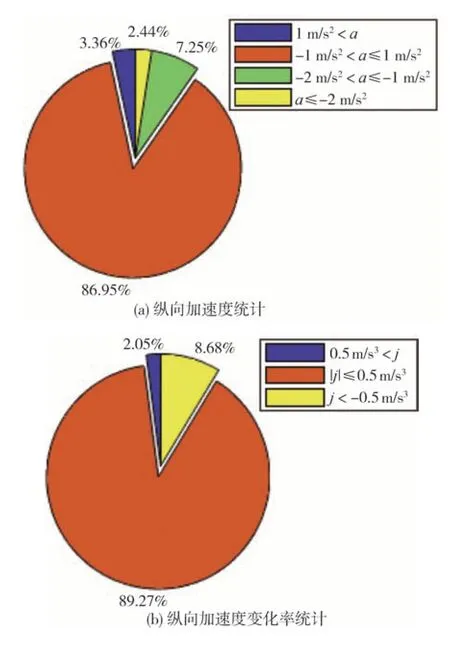
图10 AIWAYS M891鲁棒性路试结果

4 结论

本文提出了一种面向量产的自适应巡航控制系统纵向加速度规划方法。通过多维优化PID 控制方法，适配多时距配置，降低参数标定量，解决传统定速巡航算法待标参数多不易工程量产的问题。采用基于动态预测时域的模型预测控制方法进行跟车巡航加速度规划。通过处理目标车加速度及考虑执行器效率和时延，提高了系统安全性。对MPC 算法进行了优化：一方面对预测时域进行动态管理，具备多场景自适应多车型适配的高通用性；另一方面对代价函数进行优化，降低求解复杂度，满足低算力控制器对算法低资源占用的要求。通过多款量产车型的道路试验，分别从定速巡航、跟停静止前车、旁车切入的各场景测试数据和1 万km 路试统计数据两个维度，验证了该规划方法可保证高安全性、高舒适性和高可靠的量产要求，具备场景自适应性和多车型适配的高通用性。