三相PWM变换器电流切换预测控制仿真及实验研究

郭 鑫， 程 刚， 焦尚彬， 刘 军

（西安理工大学自动化与信息工程学院，西安 710048）

0 引 言

三相脉冲宽度调制（Pulse Width Modulation，PWM）变换器被广泛应用于新能源并网、电动机调速、电动汽车和有源滤波器等各领域［1-3］，建立精确的数学模型并设计先进控制策略以提升三相PWM 变换器控制性能是其研究的主要方向［4-6］。

目前，无论在教学还是科研中，应用最为广泛的电力电子变换器建模是线性化后统一建模［7-8］。普遍采用的状态平均小信号建模方法［7］，通过忽略变换器开关器件的开关频率特性，在一个采样周期内对系统各变量（例如电压、电流）进行平均，建立占空比、输入电压的低频变化对变换器中的电压、电流影响的小信号线性化模型。基于状态平均的小信号线性化建模方法物理意义清晰，便于稳定性分析，可运用经典控制理论进行控制器设计。传统小信号平均模型是通过忽略模型中高次项而近似得到，无法实现对变换器工作状态的精确描述，并存在大信号扰动时不稳定等诸多问题［9］。基于传统线性模型的三相PWM变换器控制方法，如广泛使用的三相PWM 变换器双闭环比例积分（Proportional Integral，PI）解耦控制方法［10-12］，其控制器设计需求复杂的旋转坐标变换及正弦脉冲宽度调制（Sinusoidal Pulse Width Modulation，SPWM）或空间矢量脉冲宽度调制（Space Vector Pulse Width Modulation，SVPWM）过程。同时，传统双闭环PI解耦控制方法存在着控制参数多、整定困难，仅能保证线性工作点附近的系统控制性能等。

近年来，切换系统理论在电力电子技术中的应用和发展为解决上述问题提供了新的视角。通过将工作在不同开关状态下的变换器视为不同的子系统，三相PWM变换器可视为一类典型的切换系统。文献［13］中建立三相有源电力滤波器（Active Power Filter，APF）的切换仿射线性模型，并基于共同李雅普诺夫函数（Common Lyapunov Function，CLF）的凸组合理论提出了针对三相APF 切换模型的稳定性分析定理。在保证变换器不同子系统切换稳定性的条件下，通过切换规则直接选取下一控制周期最优的子系统（开关状态），实现三相APF的直接切换控制。文献［14］中在建立三相PWM 变换器切换模型基础上，进一步改进李雅普诺夫函数选取并进行了系统稳定性分析。作者前期成果建立了三相电网不平衡条件下的三相PWM变换器切换模型，并基于切换模型设计切换控制器实现三相电网不平衡条件下的直接电流切换控制［15］。

由基于切换系统理论的三相PWM 变换器切换控制研究成果可见［13-15］，相较于传统三相PWM 变换器线性化模型，切换模型的建立无近似化、平均化等操作，能够精确描述变换器工作过程。同时，基于切换系统模型及稳定性分析结论设计切换规则，直接控制变换器在不同子系统间切换控制的控制模式，避免了复杂的坐标变换及矢量调制过程，且具有控制参数少，响应速度快的优势。此种基于切换模型，在每个采样周期直接控制变换器在不同子系统间切换的控制模式，使得变换器开关频率不固定且需求高采样频率。因此，电力电子变换器切换控制方法，存在教学及实验研究中受限及无法直接应用于软开关变换器等问题。

针对传统三相PWM变换器切换控制中存在的开关频率不固定且需求高采样频率，提出一种三相PWM变换器电流切换预测控制（Current Switching Predictive Control，CSPC）策略，在保留切换模型及切换控制策略原有优势的基础上，降低系统采样频率需求并实现变换器定频切换控制。仿真和实验结果证明了所提方法的有效性。

1 三相PWM变换器电流切换预测控制方法

1.1 电流切换模型建立

三相PWM变换器如图1 所示，其中：ua、ub、uc为三相输入交流电压；ia、ib、ic为三相输入交流电流；La=Lb=Lc=L为三相输入交流滤波电感；R 为电感及开关元件的等效电阻；S1～S6为功率开关器件；C为输出滤波电容；RL为直流侧负载，Udc为输出直流电压。

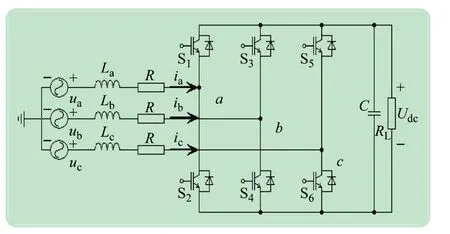
图1 三相PWM变换器结构

建立三相PWM 变换器电流切换误差模型［10-11］（包含电流误差动态连续模型及离散切换模型两部分）：

表1 三相PWM变换器子系统划分

1.2 电流切换预测控制方法

基于式（1）三相PWM变换器电流切换误差模型，可通过如下引理分析切换系统稳定性并设计切换控制器（切换规则）［10-12］。

引理1对于具有M≥2 个子系统的切换系统式（1），如果存在凸组合λ=［λ1，…，λM］∈（0，1）满足

则在切换规则

证明详见文献［10-12］。

基于引理1，为简化三相PWM变换器切换稳定性分析，一个输入电压周期可按60°间隔被划分为6 个扇区，如图2 所示。

由三相PWM 变换器工作原理可知，对于图1 工作在整流模式下的三相PWM 变换器，在电压相角为0° ～120°时（即图2 扇区1、2），相电压uc＜0，变换器能量流动主要由a、b相提供，在此区间应控制Sc=0。同理，在电压相角度为120° ～240°时，Sa=0，240° ～360°时，Sb=0。因此，以扇区1 为例，根据表1，此时三相PWM变换器可看作为由子系统V1、V3、V5、V7组成的切换系统。进一步，依据最小切换原则，子系统V3=［SaSbSc］=［0 1 0］与V5=［SaSbSc］=［1 0 0］间的切换应避免。扇区1 时，三相PWM 变换器切换系统组合可分为2 组，即（V1，V3，V7）和（V1，V5，V7）。由文献［10-12］中的切换稳定性分析可知，扇区1 中，子系统V1、V5、V7间的切换满足引理1 切换稳定性条件，而子系统V1、V3、V7间的切换不满足引理1 切换稳定性条件。同理，对于6 个扇区均进行切换稳定性分析，可获切换矢量表（见表2）。

依据表2 及引理1，通过判定三相输入电压相互关系，从表2 中选择对应扇区3 个子系统并通过式（3）切换规则，选择切换规则函数最小子系统作为下一控制周期最优子系统，便可实现三相PWM 变换器切换控制。在每个采样周期选择切换规则函数值最小子系统作为下一控制时刻变换器开关状态的方式，因可能出现连续相同最优子系统状态，导致开关频率不固定。

为此，将一个固定采样周期Ts划分为N 个子区间。在每个子区间，依据该子区间开始时刻三相输入交流电压、电流状态，按表2 及改进的切换规则函数，实现该子区间最优子系统选择。改进切换规则函数

因此，第n+1 个子区间开始时刻三相PWM变换器电流误差状态预测值

基于式（5）、（6），可获得一个开关周期内N 个子区间电流误差状态预测值。

基于改进切换规则式（4）及电流误差状态预测式（5）、（6），可预测获得固定采样周期Ts内N个子区间的最优子系统状态。通过对N =4 个子系统状态重组获得定频开关波形，如图3 所示。

图3 固定开关周期内4个区间最优子系统重构示意

由图3 可见，依据PWM 面积等效原则，一个固定开关周期内的2 种开关波形，对于变换器的激励效果相同。当预测获得固定开关周期内N 个区间的最优子系统状态时，可根据实际系统控制需要生成任意所需的开关状态波形，同时保证开关频率固定。

综上，采用所提CSPC 方法的程序流程如图4 所示，系统结构如图5 所示，其中电压外环控制器采用传统PI控制方法，电流内环控制器采用CSPC 方法。图5 中，Udcr为三相PWM变换器输出直流电压Udc的期望值，idr为电压外环控制器输出有功电流期望值，iqr=0为无功电流期望值，将idr及iqr经反旋转坐标变换后，可获得电流内环CSPC控制器所需三相交流电压期望值iar、ibr、icr。

图5 采用CSPC方法的系统结构框图

2 仿真及实验分析

2.1 仿真分析

本文三相PWM 变换器仿真模型搭建基于Matlab，电路参数及控制参数见表3，其中电压环PI控制参数采用混沌粒子群优化方法［7］优化获得。基于表3 参数，采用所提CSPC控制策略的三相PWM变换器仿真结果如图6 所示。

表3 仿真参数

图6 标称电路参数条件下采用本文控制方法的三相PWM变换器仿真结果

图6 中，图6（a）为输出直流电压波形，图6（b）为三相输入电压、电流波形，图6（c）为开关S1波形，图6（d）为开关的快速傅里叶变换（Fast Fourier Transform，FFT）分析结果。

由图6（a）、（b）可见，采用传统电压环PI 控制器结合本文所提CSPC 方法的三相PWM 变换器输出直流电压快速到达期望值且无稳态误差，输入三相电流波形呈正弦且跟随输入电压变化，即实现单位功率因数控制。由图6（c）可见，基于CSPC方法的三相PWM变换器开关波形满足切换矢量表2 条件，即对应电压扇区中有一个桥臂开关管不动作。由图6（d）频谱分析可见，所提方法开关频率为10 kHz。作为比较，文献［10］中传统切换控制方法的三相PWM变换器开关波形及频谱分析结果如7 所示。由图7（a）可见，传统切换控制方法的开关频率不固定。如图7（b）可见，其开关频率谱分布于0 ～40 kHz 区间。经测量得，此时平均开关频率约为10 kHz，与所提CSPC 方法相近但采样频率为CSPC方法的4 倍。比较图6、7 仿真结果可见，所提CSPC方法实现了三相PWM变换器定频切换控制并降低了系统采样频率，同时保留了传统切换模型的切换控制策略控制参数少，无须复杂矢量调制过程等优点。

图7 文献［10］中传统三相PWM变换器切换控制策略开关状态及其FFT分析仿真结果

2.2 实验分析

为验证所提CSPC方法有效性，搭建1.2 kW实验样机，其控制器编程采用DSP 28 335，功率因数测量采用HIOKI 3197 型功率因数分析仪。

对应图6 仿真结果的所提CSPC 控制策略实验结果如图8 所示。

图8 标称电路参数条件下采用本文方法的三相PWM变换器实验结果

图8（a）中上图为三相PWM变换器输入a相电压ua、电流ia波形，下图为图8（a）局部放大波形；图8（b）中上图为三相PWM变换器输入a 相电压ua波形及对应的开关S1波形，图8（b）中下图为开关S1波形的FFT结果。

由图8 可见，采用所提CSPC方法的三相PWM变换器输入a相电流波形呈正弦变化且与a相电压相位保持一致，功率因数（PF）为0.995，达到了单位功率因数控制要求。同时，通过采用多步切换子系统状态预测并重组的方法，所提CSPC 方法开关S1波形随电压输入扇区变化而变化且达到了10 kHz的固定开关频率要求，如图8（b）FFT 分析结果及左下角频率测量结果所示，实现了三相PWM 变换器的定频切换控制。图8 实验结果与图6 仿真结果一致。

3 结 语

基于切换系统理论的电力电子变换器建模和控制方法，因其能够从本质上反应变换器特征而受到关注。基于传统切换系统理论的电力电子变换器建模及控制方法存在开关频率不固定，需求高采样频率，无法应用于软开关变换器等，在教学及研究中应用受限。就此，提出一种针对三相PWM变换器的电流切换预测控制策略，通过在固定采样周期中实现多步系统状态及最优子系统预测并进行开关状态重组的方式，实现三相PWM 变换器定频切换控制并降低了采样频率要求。仿真及实验结果验证了所提方法的有效性。