挖掘机液压系统非线性摩擦的辨识与补偿
2023-11-09杨超赵佳伟马伟殷晨波杨中良王大宇
杨超,赵佳伟,马伟,殷晨波,杨中良,王大宇
(1.南京工业大学车辆与工程机械研究所,江苏南京 211816;2.三一重机有限公司,江苏苏州 215300;3.三一集团有限公司,湖南长沙 410000;4.中国工程机械工业协会,山西太原 030000)
0 前言
因挖掘机广泛应用于道路建设、桥梁建设等各种高难度作业工况,常出现工作效率降低现象。液压系统本身的一些非线性因素也会影响挖掘机效率[1],因此对非线性因素的补偿控制对于挖掘机显得尤为重要。本文作者以挖掘机铲斗联液压缸的摩擦为研究对象,来改善液压系统性能和控制精度。
目前,KAZEMI、YAZDIZADEH[2]根据Lyapunov理论估计摩擦力的大小,并基于此对摩擦力进行补偿。北京理工大学的毛锐[3]选取Stribeck摩擦模型,借助理论分析将摩擦力转化为液压缸的压力,从而得到Stribeck曲线,最后设计出动态补偿控制器来对系统的摩擦进行有效补偿。TAN等[4]使用输出反馈自适应鲁棒控制解决液压缸缸体与活塞之间的摩擦力和参数不确定性问题。毛尾等人[5]为了消除液压缸摩擦力的影响,使用遗传算法离线辨识出摩擦力模型,并在系统中添加位移传感器实时采集液压缸速度,计算出了摩擦力并进行补偿。山东大学的孙建浩[6]结合改进的鱼群算法对直驱阀进行了摩擦参数辨识,通过摩擦前馈补偿的方式改善了系统的位置控制精度。
虽然众多算法相继出现,但受到硬件和算法本身缺陷的限制,在低速运动时非线性摩擦力对系统影响较大,需提高控制精度以满足需求。为对摩擦力进行更精细的补偿,本文作者选择基于摩擦模型的前馈补偿策略,其结构设计简单且可避免相对速度为零时摩擦不连续的现象,所以只需辨识出相应参数即可取得较好的补偿结果。以改进的Stribeck摩擦模型为基础,结合粒子群算法和摩擦前馈补偿策略,改善了由于摩擦导致的液压缸低速爬行和平峰现象,提高了轨迹跟踪精度。
1 电液比例阀控缸系统模型
1.1 电液比例阀控缸系统的组成
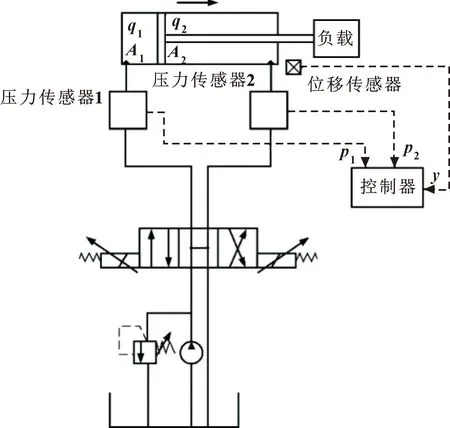
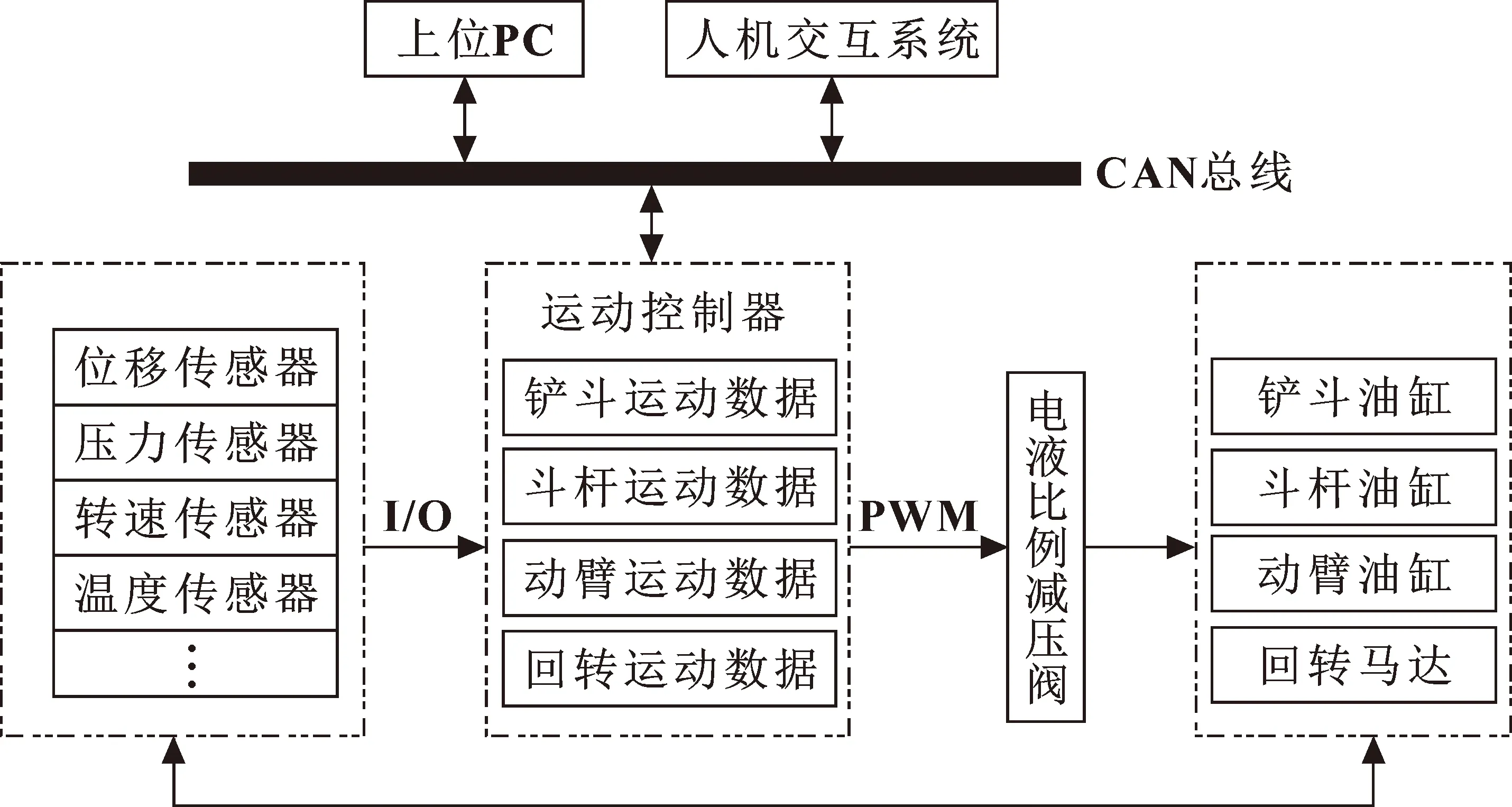
挖掘机电液比例系统可分为手柄、控制器、比例放大器、电液比例阀、液压源和传感器等[7]。系统结构如图1所示,可分为4个部分:挖掘机操作手柄向控制器生成控制信号,由放大器转换为电信号控制先导阀,主阀根据先导阀的运动进而控制液压缸运动,此时,位移传感器再将位移信号反馈给控制器。

图1 电液比例阀控缸系统结构
动臂、铲斗和斗杆三部分的建模原理完全一样,只是特定参数不同。考虑到实际中铲斗联更接近工作对象,故选取挖掘机铲斗联的伸出动作作为研究内容。
1.2 电液比例阀控缸系统的建模
1.2.1 液压缸环节
非对称液压缸中的摩擦是影响控制性能的主要因素,而其他摩擦因素可以忽略[8]。为简化过程,以下皆是在杆外伸的基础上进行研究。
阀控非对称液压缸的结构简图如图2所示,其中xv表示比例方向阀阀芯位移;A1、A2分别表示液压缸无杆腔和有杆腔工作面积;V1、V2分别表示液压缸无杆腔和有杆腔体积;p1、p2分别表示液压缸无杆腔和有杆腔工作压力,pP表示主泵供油压力,pT表示回油压力;q1、q2分别表示液压缸无杆腔和有杆腔流量;y表示液压缸活塞杆位移。
在建模过程中,以活塞杆外伸为正方向,液压缸两腔的工作面积比为n,则可以定义负载压力pL和负载流量qL。这两者的定义如式(1)所示:
(1)
式中:n=A2/A1。
为简化分析过程并突出重要概念,以下是非对称液压缸的3个基本方程[9]。
(1)负载流量方程
根据薄壁小孔的节流公式和定义式可得液压缸负载流量方程:
(2)
式中:Cd为多路阀流量系数,根据阀口形状一般取0.6~1;ω为多路阀阀口面积梯度;xv为多路阀阀芯位移;ρ为液压油密度。
(2)非对称液压缸流量连续性方程
对密闭容器中油液进行分析,可以得到流量连续性方程:
(3)
式中:∑qin为流入液压缸的流量和;∑qout为流出液压缸流量和;y为液压缸活塞位移;V为液压缸容积;p为液压缸压力;βe为油液体积弹性模量。
(3)非对称液压缸力平衡方程
假设液压缸受力为理想情况,非对称液压缸在工作工程中的力平衡方程:
(4)
式中:mp为负载质量;Bp为活塞的黏性阻尼系数;Kp为弹性外负载等效弹簧刚度;F为负载力;Ff为摩擦力。
1.2.2 放大器、反馈环节
放大器、反馈环节皆可看成一个比例环节,两个环节的数学公式为
(5)
式中:Uc为位移传感器反馈电压,Kc、Ka分别为传感器放大增益和比例放大器增益;U为手柄输出电压;I为比例电磁铁输入电流。
1.2.3 比例阀环节
比例阀作为液压控制部件,该环节的数学公式为
(6)
式中:Xv为多路阀阀芯位移;I为比例放大器输出电流;Kb为电流增益系数;T为时间常数,s为拉普拉斯算子。
1.3 非线性摩擦模型的建立
在实际的摩擦测量实验中发现,液压缸在低速运动过程中,摩擦力随着速度的增大而减小。该特性符合图3所示的Stribeck摩擦力曲线[10]。
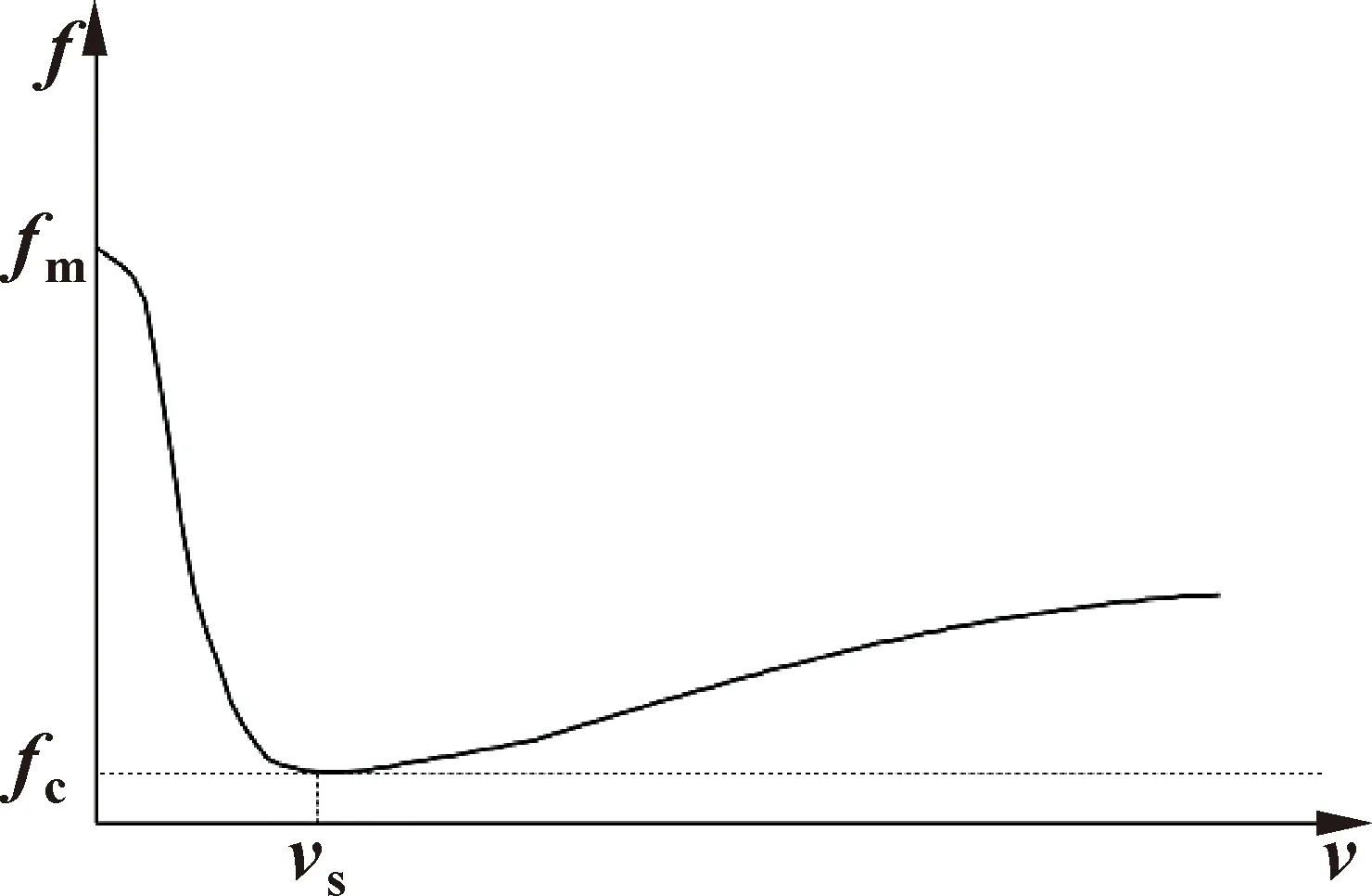
图3 Stribeck摩擦力曲线
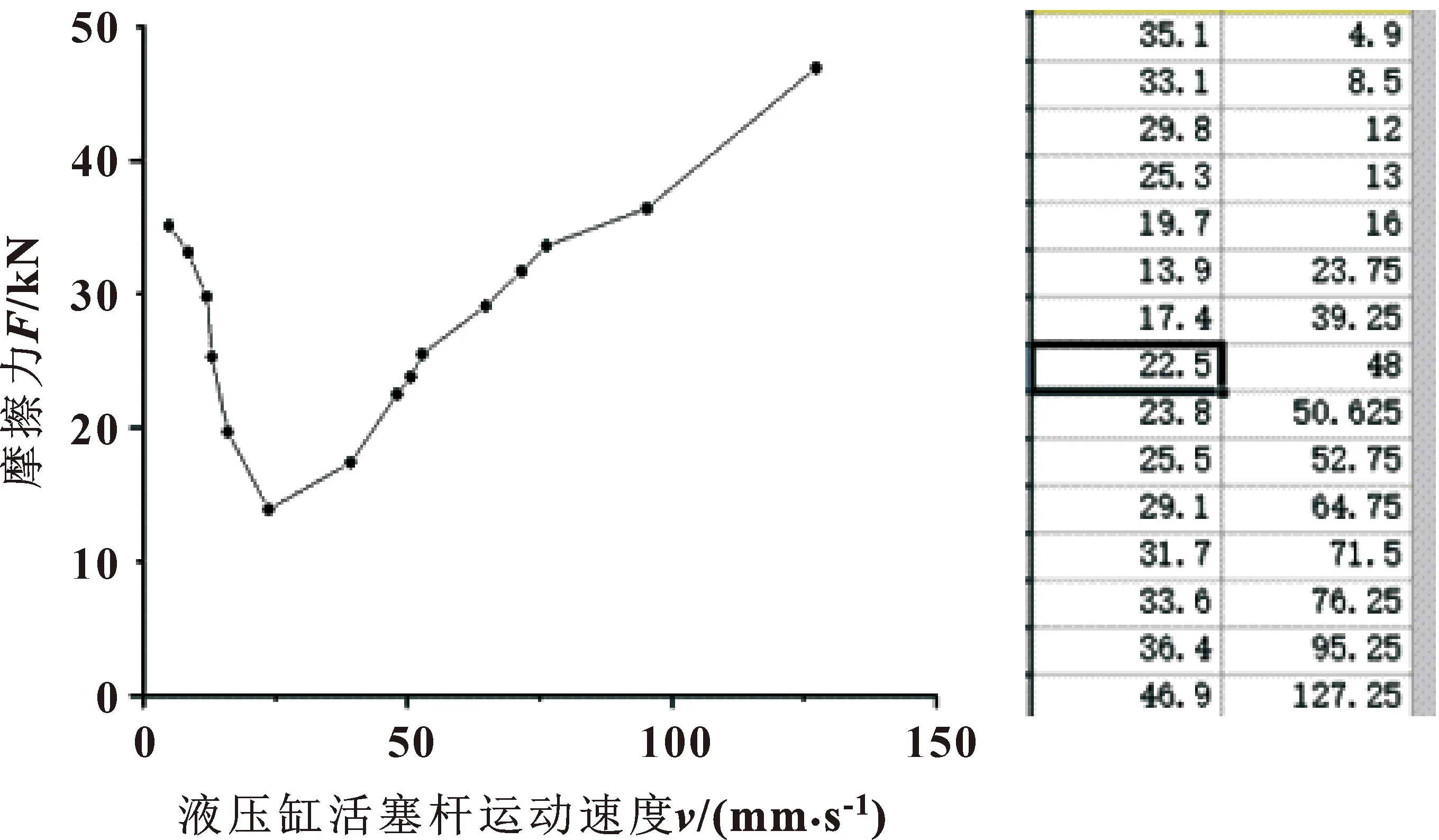
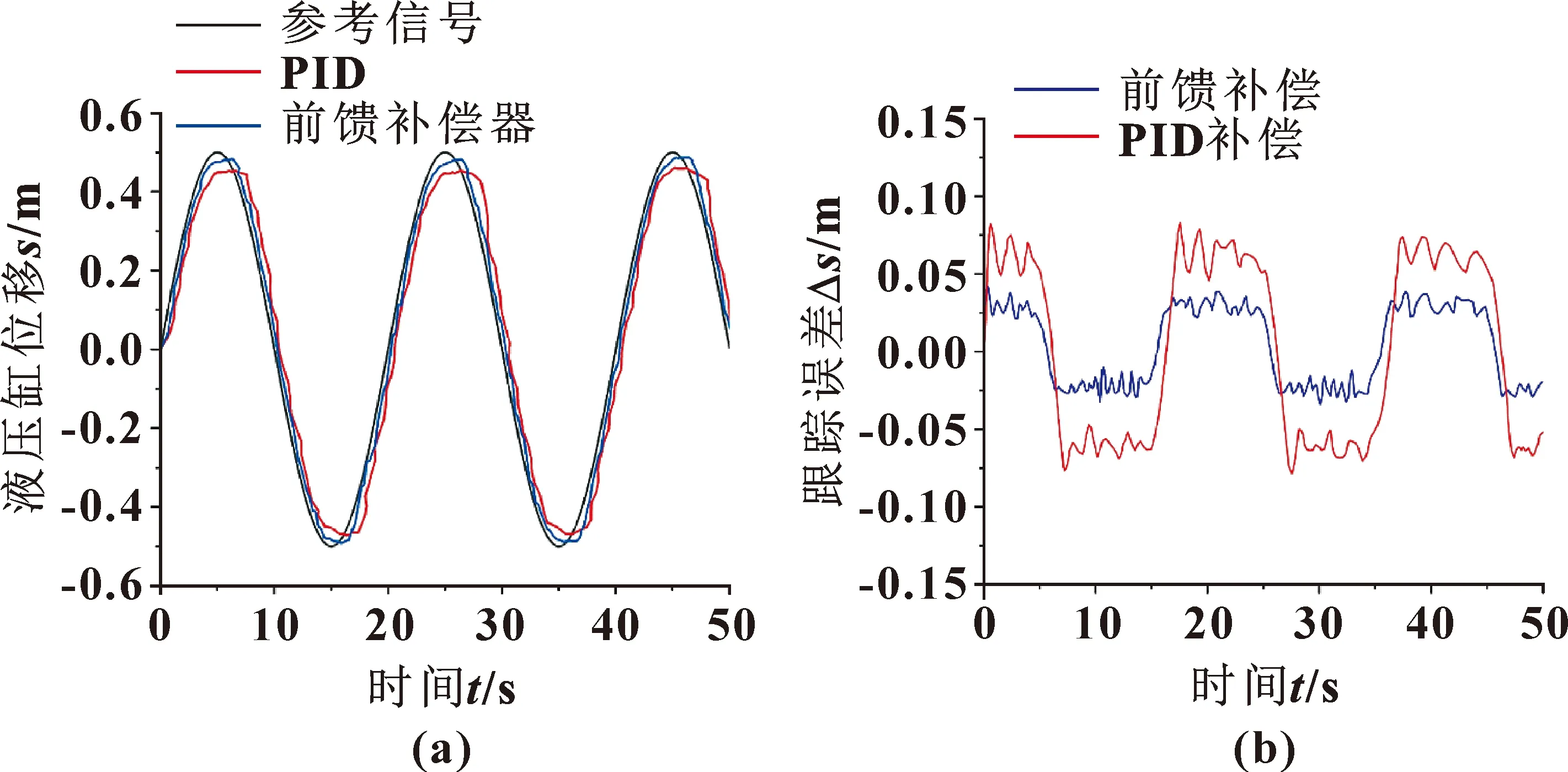
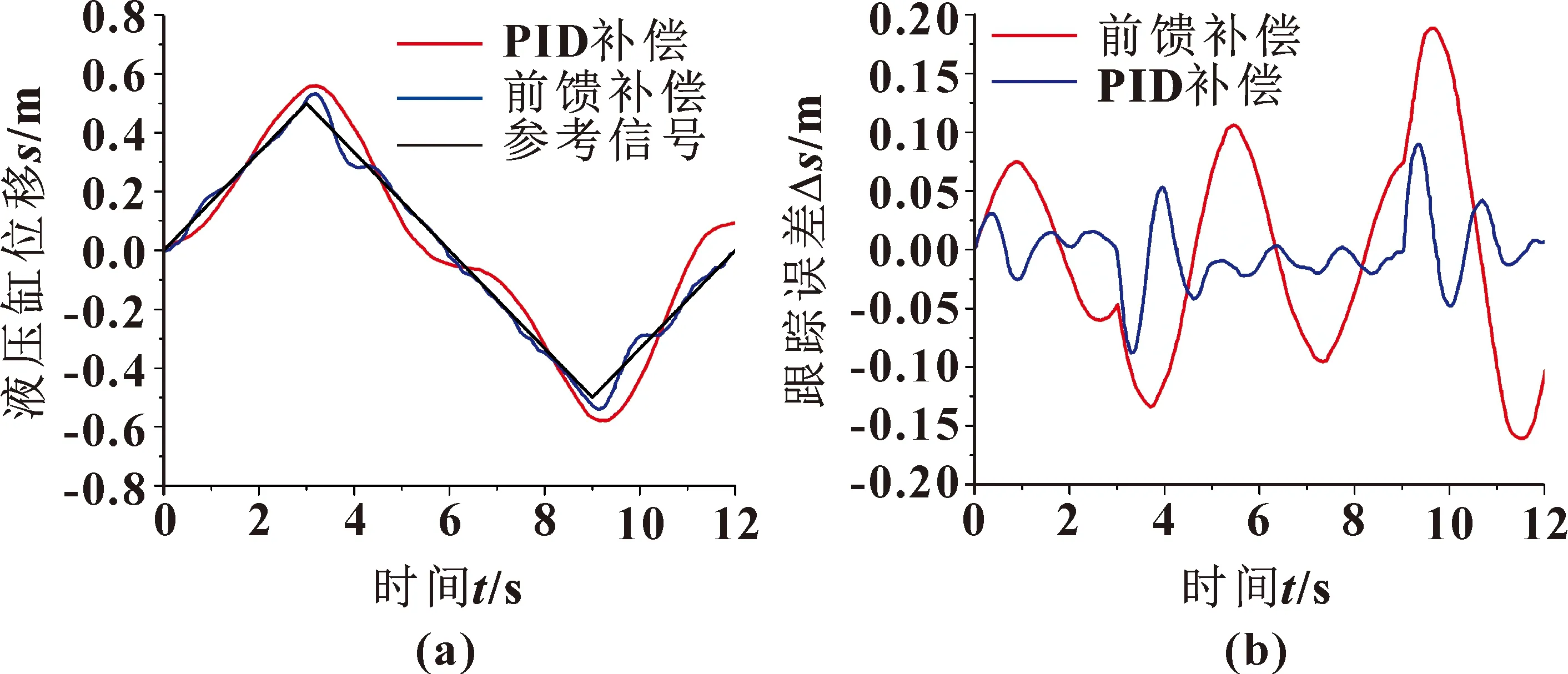
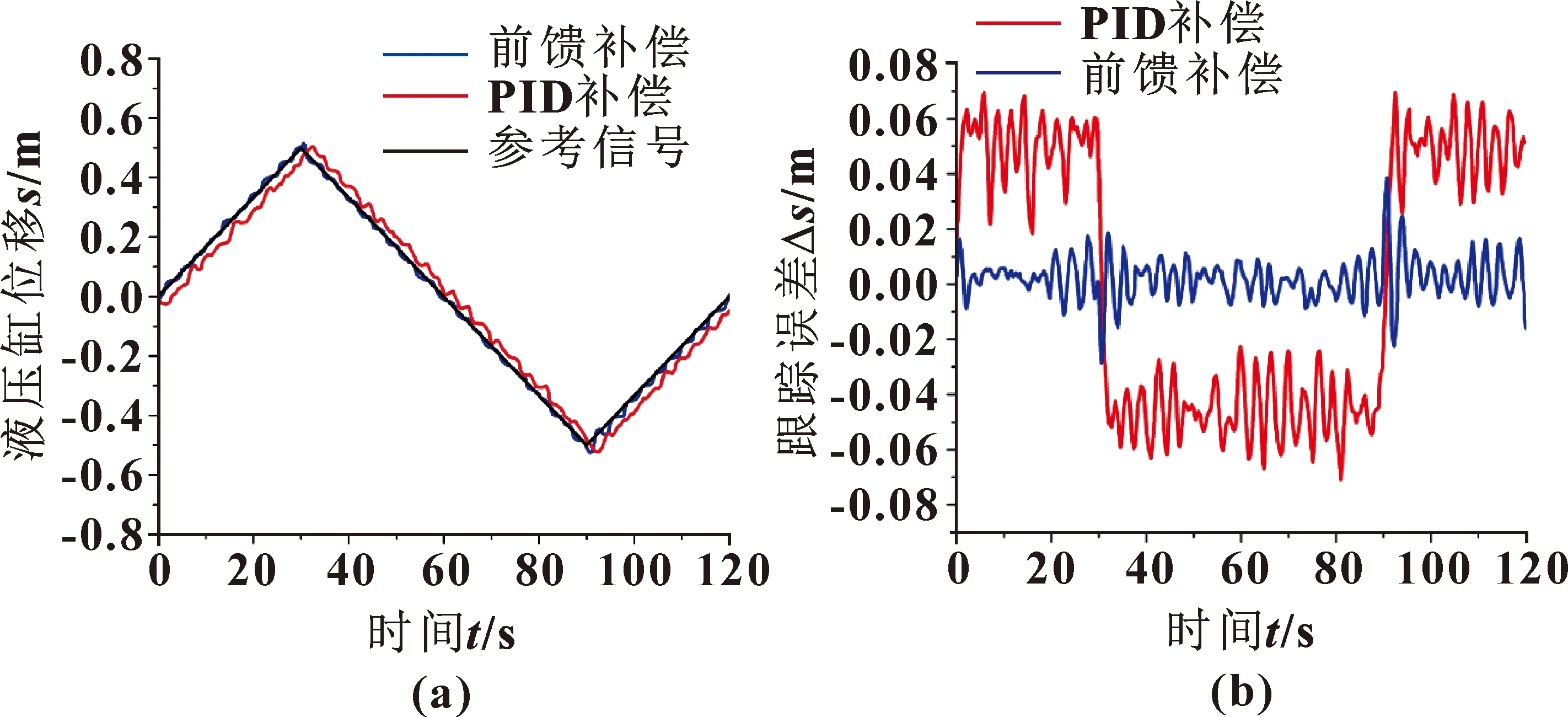
当物体速度为零时,摩擦力大小由合外力决定。为避免产生相对速度为零时摩擦力不连续现象,参考Karnopp模型的思想,将不连续函数替换成连续函数。在零速度附近设置一个速度阈值vc(0 改进的摩擦模型如图4所示:fm为最大静摩擦力,它是经过速度阈值与原Stribeck曲线所作垂线的交点;当速度大于拐点vs后,摩擦力与速度呈线性关系,直线斜率为黏滞摩擦系数σ;将该直线反向延长,与摩擦力轴相交得到的点为库仑摩擦力fc。 图4 改进的Stribeck模型 改进的Stribeck摩擦模型如式(7)所示,式中待辨识的参数有Fc、Fm、vs和σ。 (7) 辨识实验在国产某235 kN的挖掘机上进行,如图5所示。液压缸两个腔室内的工作压力可通过压力传感器获得。同时,可以通过安装在气缸上的拉线位移传感器测量气缸的位移。 图5 某国产挖掘机实验平台 当液压缸恒速运动时,加速度为零,系统驱动力用来克服摩擦力和负载力。此时挖掘机无弹性负载,力平衡方程如式(8)所示: F=A1p1-A2p2-Fe (8) 式中:液压缸活塞杆面积A1、A2与外负载力Fe均为固定值。 测试回路如图6所示,将铲斗液压缸的位移输入信号设定为三角波信号,此时液压缸可以保持恒速运动。再通过压力传感器采集液压缸两个腔室工作压力,即可得到不同恒定速度下液压缸压力随时间变化变化曲线,如图7所示。 图6 摩擦力实验测试回路 图7 铲斗液压缸有杆腔和无杆腔工作压力曲线 根据图7测量到的铲斗液压缸大小腔不同速度下的压力以及挖掘机液压缸结构的尺寸大小并结合其有效工作面积,利用力平衡方程式(8)即可间接得到液压缸摩擦力数值大小,并生成点线图,如图8所示。 图8 摩擦力数值曲线 为简化目标函数,选取速度阈值之外的摩擦模型部分,可以得到式(9): Fc+(Fm-Fc)e-(v/vs)2+σv=A1p1-A2p2-Fe (9) 以铲斗联为例,前文建立了相应模型并获得了摩擦力,但准确性还需要参数辨识实验进行验证。参数辨识可以认为是在所有解空间中寻找一组最优参数,即通过合适的辨识算法确定未知参数(Fm、Fc、vs和σ),参数辨识的误差见式(10): e=A1p1-A2p2-Fe-(Fc+(Fm-Fc)e-(v/vs)2+σv) (10) 本文作者选取如式(11)所示的最小平方和作为目标函数J: σv))i]2 (11) 式中:i为测量值的序号;n为总测量数。 利用EBERHART和KENNEDY提出的粒子群算法来辨识摩擦模型中的参数(Fm、Fc、vs和σ)。该算法的核心是通过整体中每个个体之间的协作,以局部最优点为出发点寻找到全局最优[11]。然而,经典的粒子群算法仍有一些不足,如结果精度低、算法后期容易导致早熟收敛等。为克服这些缺点,在学习因子c1和c2以及惯性权重ω上做出调整[12]。 (1)针对算法容易陷入局部最优解的情况,对学习因子做出改进。当优化问题较为简单时,按照经验学习因子一般取2。当问题较为复杂时,算法初期,为了使寻优粒子能够快速聚集于最优解附近,c1取较大值,c2取较小值;在算法后期,为了使寻优粒子快速收敛到全局最优解附近,c1取较小值,c2取较大值。学习因子的计算公式如式(12)所示: (12) 式中:t为当前迭代数;tmax为算法总迭代数;c1i=2.5,c1f=0.5,c2i=0.5,c2f=2.5。 (2)针对算法容易早熟收敛和局部寻优能力差的问题,对惯性权重ω做出调整。在算法前期需要较大的惯性权重,提高全局搜索能力;在算法后期减小惯性权重,提高粒子局部搜索能力。按照经验,惯性权重的取值从0.9非线性递减至0.4。改进后的粒子群算法如式(13)和(14)所示: vid(t+1)=ωvid(t)+c1r1(pbest,id-Xid(t))+ c2r2(gbest-Xid(t)) (13) Xid(t+1)=Xid(t)+vid(t+1) (14) 惯性权重ω的取值如式(15)所示: ωmin)t/tmax (15) 式中:ωmax取0.9,ωmin取0.4。 利用改进的粒子群算法可找到最优参数,挖掘机铲斗联非线性摩擦参数的辨识算法流程如图9所示。系统的输入为摩擦模型计算的理论摩擦力与实际测得的摩擦力,算法的整体目标是使两者差值最小,达到拟合的目的。 图9 改进粒子群算法摩擦辨识流程 参数辨识中的相关参数如表1所示,表中参数是最优参数范围,Fm、Fc、vs和σ的初始值可根据实际测得的摩擦力曲线确定。 表1 参数辨识中的相关参数 非线性摩擦参数及最佳目标函数辨识结果如表2所示。非线性理论摩擦力与实际摩擦力比较如图10(a)所示,粒子群算法收敛曲线如图10(b)所示。 表2 摩擦力参数辨识结果 图10 参数辨识结果(a)及收敛曲线(b) 如图10(a)所示:辨识出的摩擦力和实际测量结果基本一致,理论非线性摩擦模型基本可以描述铲斗联实际摩擦现象。两种粒子群算法的收敛曲线如图10(b)所示:改进的粒子群算法经过105次迭代后收敛,而经典的粒子群算法则经过了232次迭代,在两种算法下的误差均方根分别为1.73和2.88,改进的方法对比未改进的方法误差减小了39.93%。综合数据,改进的粒子群算法取得了较理想的辨识效果。 根据建立的摩擦模型和辨识出的摩擦参数,选择基于摩擦模型的补偿策略对摩擦进行前馈补偿[13]。前馈补偿,就是在原有对模型和参数的准确掌握下,在系统中增加补偿力,消除摩擦的影响[14]。具体的补偿策略框图如图11所示。 图11 基于摩擦模型补偿的控制框图 在进行摩擦力补偿时,液压缸速度的精确测量十分重要。为解决位移传感器受到噪声干扰后,产生速度测量误差的现象,本文作者设计跟踪微分器,将微分转化为积分从而得到精确的液压缸速度信号,旨在从带有干扰的信号中得到连续信号及其微分,进而提高速度估计精度。 设跟踪微分器测得的输入的液压缸位移信号为r(t),系统输出信号为x1(t)、x2(t)。其中,x1(t)为r(t)的跟踪信号,x2(t)为r(t)的微分,则可得: (16) 式中:sat为饱和函数,δ为线性区间范围,表达式为 (17) 实际应用中,需要对速度观测器进行离散化处理并用于数字控制,可得: (18) 式中:Ts、R和h分别为积分补偿、速度参数和滤波参数,函数fst如式(19)所示: fst(x1(k)-r(k),x2(k),R,h)= (19) 式中: (20) 式(20)中:速度因子R和滤波因子h是速度观测器中与速度跟踪性能有关的两个可调参数。R值越大,速度观测器滞后越小,但减弱了抗噪声的能力;h值越大,抗干扰能力越强,但相位滞后越大。综合这些因素,令R=40,h=1[15]。 根据结构不变性原理,提出摩擦前馈补偿方案如图12所示,铲斗联相关参数如表3所示。摩擦力和负载会导致负载压力的变化从而影响多路阀流量和液压缸位移,因此将负载压力pL设为观测值并设计前馈补偿器。 表3 摩擦力前馈补偿相关参数 图12 非线性摩擦力前馈补偿框图 图12中虚线部分为前馈补偿器,可改善摩擦对控制的影响,摩擦力和外负载通过补偿器被引入到阀的前端。实际上,补偿通道是一个通过扰动补偿的开环系统,可补偿全部或部分扰动。 补偿器E可表示为 (21) 为验证基于改进的Stribeck模型前馈补偿的有效性,选择挖掘机铲斗联为研究对象,在如图13所示的平台上分别采用传统PID控制和前馈补偿方法,通过对比来验证前馈补偿器的有效性。 图13 运动控制系统的硬件结构 从摩擦模型和前馈补偿分析中可以看出:高速时摩擦基本稳定,低速时非线性较强。因此,在进行实验时,应寻找一种既能考虑高低速,又能对低速有局部描述能力的信号。由于正弦信号同时具备高速和低速性能,故选择正弦信号作为系统输入信号。 设定正弦信号的输入频率和幅值分别为0.05 Hz和500 mm,使用两种方法分别跟踪正弦信号,得到的轨迹跟踪曲线和跟踪误差如图14所示,均方根和最大误差见表4。 图14 前馈补偿器和PID控制器正弦信号轨迹跟踪曲线(a)及跟踪误差曲线(b) 如图14(a)所示,在信号的峰值处,轨迹跟踪误差最大,此时PID控制器和前馈补偿控制器的最大跟踪误差分别为75.62 mm和38.65 mm,与PID控制器相比,前馈补偿控制器峰值处的误差约为PID控制下的51%。前馈补偿控制器通过叠加信号的方式减小了摩擦对系统的影响,验证了摩擦补偿对轨迹控制具有良好的补偿效果。当位移达到峰值时,液压缸运动方向发生改变,此时摩擦力会从动摩擦转化为静摩擦最后变为动摩擦。没有摩擦补偿的PID控制器面对这种阶跃干扰无法做出响应,导致振幅平坦化现象。摩擦前馈补偿后,控制信号可以根据摩擦的大小实时变化,这相当于在原始控制信号上添加一定的附加力以消除摩擦,从而大大改善了振幅平坦化现象。 如表4所示,两者均方根误差分别为42.56 mm和19.34 mm,与PID控制器相比,前馈补偿控制器下正弦轨迹跟踪精度提高了48.8%,证明前馈补偿控制器的补偿效果更优。 设定信号的输入频率和幅值分别为0.33 Hz和500 mm,此时液压缸运动速度为167 mm/s,为高速运动状态。轨迹跟踪曲线和跟踪误差如图15所示,均方根和最大误差见表5。 表5 不同控制器下的高速运动轨迹跟踪误差 图15 高速运动下的前馈控制器和PID控制器的轨迹跟踪曲线(a)和跟踪误差(b) 高速运动下,PID控制器与前馈补偿控制器的均方根误差分别为85.33、25.12 mm;PID控制器和前馈补偿控制器的最大轨迹跟踪误差分别为148.55、80.12 mm,采用前馈补偿器时,轨迹跟踪精度提高了46%。 设定三角信号的输入频率和幅值分别为0.03 Hz和500 mm,此时液压缸运动速度为16.7 mm/s,为低速运动状态。轨迹跟踪曲线和跟踪误差如图16所示,均方根和最大误差见表6。 表6 不同控制器下的低速运动轨迹跟踪误差 图16 低速运动下的前馈控制器和PID控制器的轨迹跟踪曲线(a)和跟踪误差(b) 低速运动下,PID控制器与前馈补偿控制器的均方根误差分别为41.92、7.17 mm,未补偿的低速运动中存在低速爬行;PID控制器和前馈补偿器的最大轨迹跟踪误差分别为59.40、35.88 mm。采用前馈补偿器时,轨迹跟踪精度提高了40%。低速条件下,通过摩擦补偿,爬行的幅度和周期一定程度上减小。 上述实验结果显示:传统的PID控制器不能满足摩擦扰动的控制要求,使用摩擦前馈补偿可以改善低速爬行和振幅平坦现象。 (1)为提高挖掘机控制精度,针对挖掘机电液系统的摩擦力进行研究。通过Stribeck曲线建立非线性摩擦模型,并利用粒子群算法辨识优化参数,再基于结构不变性原理和速度观测器,设计出一种动态摩擦前馈补偿方法。 (2)通过实验,比较3种工况,得出前馈补偿相比于传统的PID控制,轨迹跟踪精度相应提高了49%、46%和40%,有效改善了摩擦引起的低速爬行和振幅平坦现象。 (3)本文作者在建立电液控制系统时,做出了一定的合理假设并忽略了一些次要因素的影响,像比例阀的中位死区和泄漏等非线性因素也会导致跟踪系统精确性的降低,所以对于挖掘机非线性补偿相关研究,还有诸多方面需要继续深入。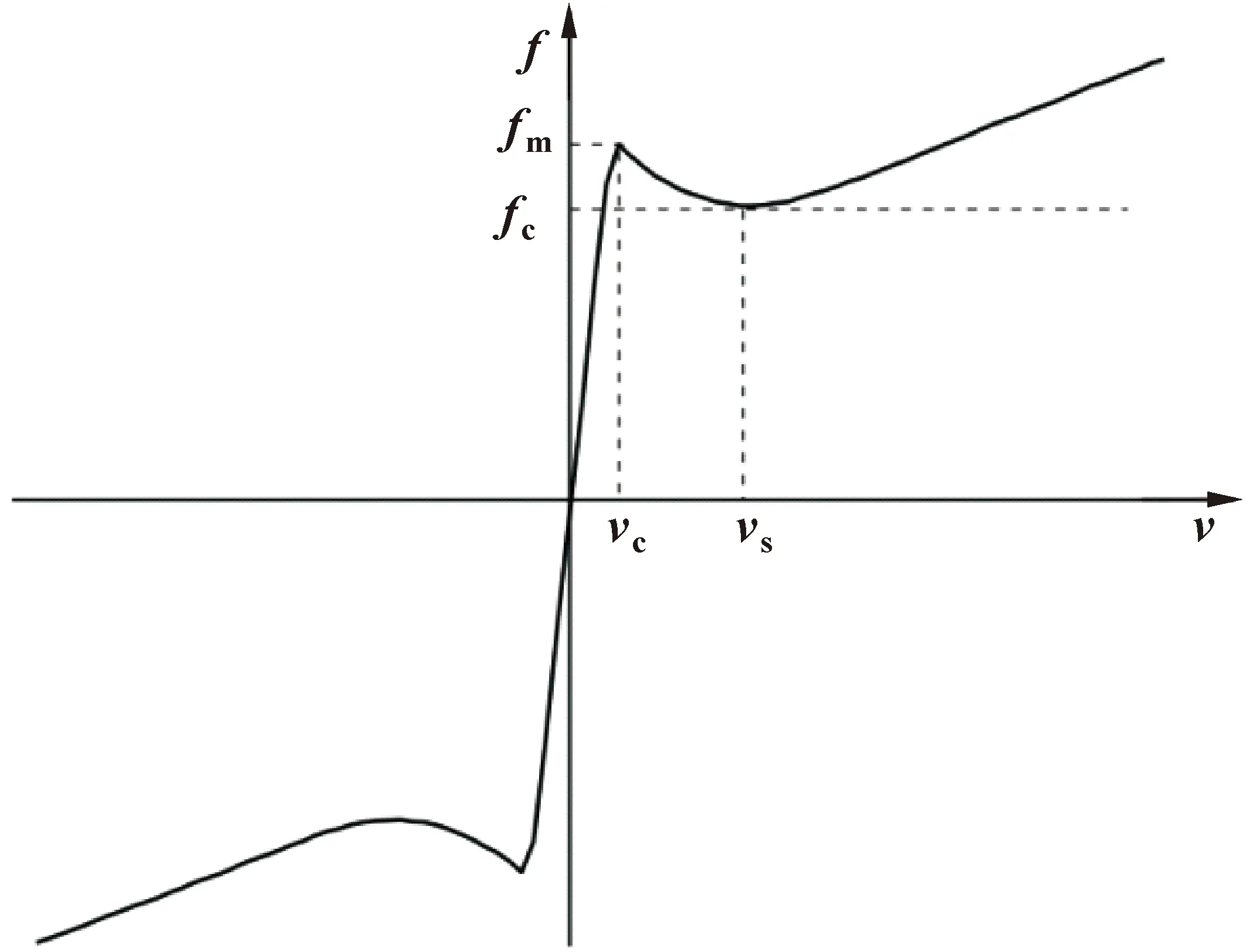
2 液压缸摩擦参数的辨识
2.1 目标函数的建立


2.2 粒子群算法
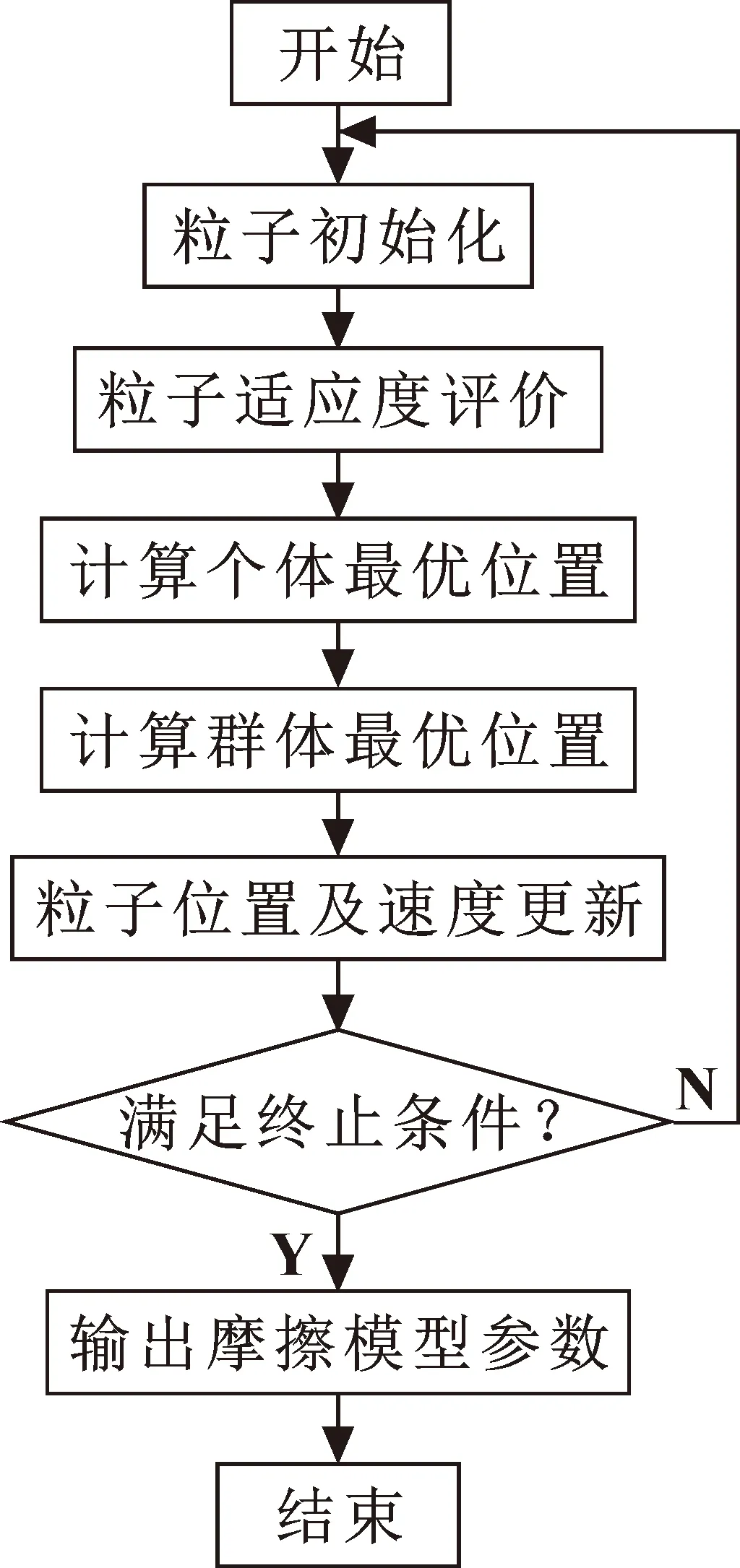

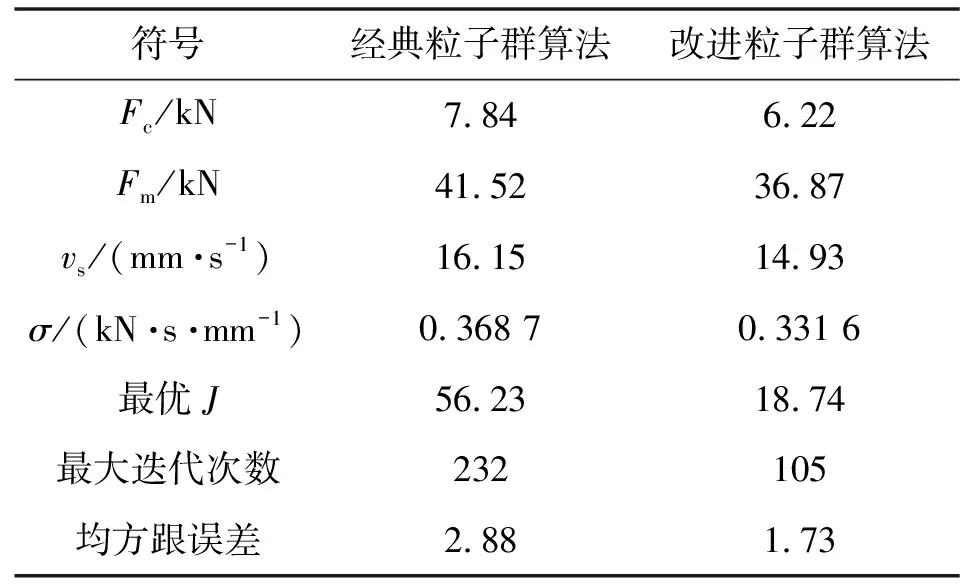
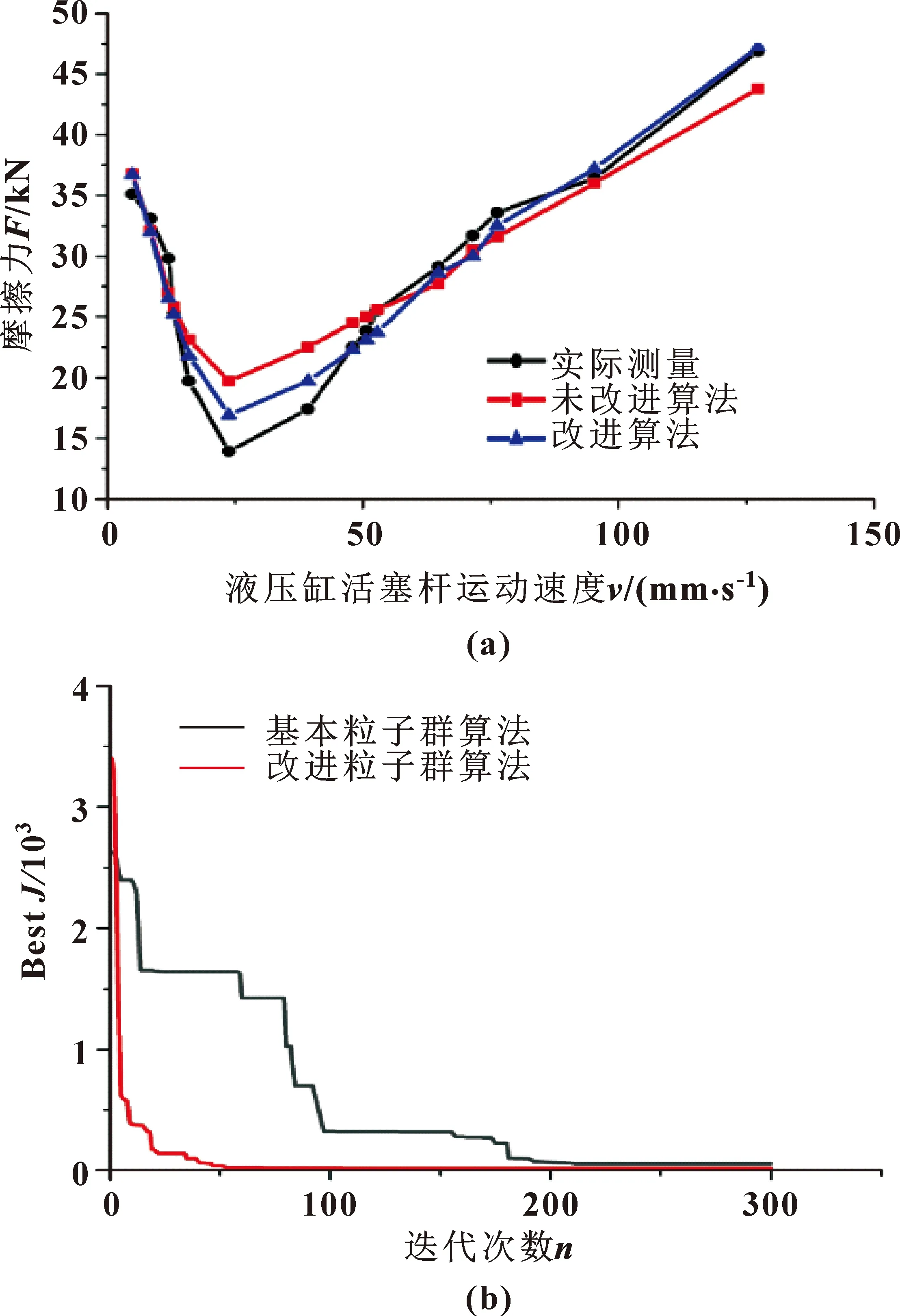
2.3 非线性摩擦模型参数辨识结果
3 非线性摩擦力补偿策略

3.1 速度观测器的建立
3.2 摩擦前馈补偿器的建立


4 非线性摩擦力补偿实验研究
4.1 实验目的和方案
4.2 正弦信号实验分析
4.3 高速运动实验分析

4.4 低速运动实验分析

5 结论
