基于RBF最小参数学习法的正流量变量泵滑模自适应控制

孙承志，张元良，康杰，牛东东

(1.大连理工大学机械工程学院，辽宁大连 116024；2.徐州徐工挖掘机械有限公司，江苏徐州 221004 )

0 前言

正流量变量泵作为液压领域中关键控制元件，常用于动力元件和执行机构的控制，其流量控制是整个电液伺服控制系统重要的组成部分[1]。而正流量变量泵通过改变输入电流使得流量自适应负载需求，减少不必要的溢流损失，以其高效、节能的工作特性被广泛应用于挖掘机、混凝土泵车等工程机械领域[2-3]。

电液伺服系统的干扰频率通常在一定范围内，系统参数的不确定性在物理系统中很常见，同时，电液伺服系统还会受到摩擦力干扰、系统泄漏等非线性因素的影响[4]。在工程领域，通常采用以下2种方法改善电液伺服系统的这些缺点：第一种是对硬件设备进行改善，比如优化系统结构和提高传感器检测精度等；第二种是提高建模的准确度，最常见的就是通过系统辨识获得模型，并在此基础上，通过合适的算法提高控制精度。为了改善电液伺服系统控制特性，许多国内外学者对伺服系统控制方法开展了深入的研究。如YAHYA等[5]在研究储罐液压伺服系统控制流量的过程中，设计液体流量控制系统中的PID模糊控制器，实现了液压伺服系统流量最佳控制响应。WANG等[6]针对发动机气体流量调节的电伺服系统，采用不完全微分PID控制方法提高系统的抗干扰能力，取得了良好的位置跟踪效果。但是以上方法对于正弦目标信号的跟踪精度不高。智能控制算法和滑模控制算法的结合有效解决了这一问题。LIU等[7]提出基于干扰观测器的滑模控制方法，在负载变化和参数不确定性的情况下依然具有良好的跟踪精度。FENG等[8]提出了基于RBF神经网络的电液伺服系统自适应滑模控制方法，采用RBF神经网络逼近和补偿电液伺服系统的模型不确定性和负载干扰，有效提高了跟踪精度。WANG等[9]提出伺服机构的自适应最优参数估计的终端滑模控制方法，引入一个辅助滤波器(提取估计误差)到伺服系统的自适应非奇异终端滑模控制中，以同时获得跟踪控制和参数估计。此外，其他控制策略主要包括无模型自适应控制[10]、输出反馈自适应鲁棒指令滤波跟踪控制[11]、终端滑模控制[12]、自适应鲁棒控制(Adaptive Robust Control，ARC)[13]和滑模遗传控制[14]等。然而，精度的提高会带来计算量的增加，对于实际应用来说很困难。

本文作者提出基于RBF最小参数学习法的正流量变量泵滑模自适应控制方法，通过参数估计代替神经网络权值的调整，极大降低控制器的计算量。同时该方法具备神经网络的快速逼近能力和滑模控制的鲁棒性，解决负载干扰和模型不确定性情况下的精确轨迹跟踪控制问题。首先，分析正流量变量泵系统的动力学特性，基于系统辨识实验，对被控系统进行系统建模。之后，对控制器进行设计并分析其稳定性。最后通过仿真实验与PID控制器和模糊PID控制器进行比较，验证系统的鲁棒性和跟踪特性。

1 正流量变量泵系统的动力学特性

正流量变量泵系统主要由电流-位移转换机构、伺服变量机构和泵排量执行机构组成。图1所示为正流量变量泵系统排量主要调节机构，箭头方向为电流增加时各个机构的运动方向。第一部分是电流位移转换机构，电磁比例减压阀将输入电信号成比例转换为压力信号，从而改变正流量活塞位移；第二部分是伺服变量机构，通过改变伺服阀芯位移，改变伺服阀出口压力，从而改变伺服活塞的大小腔压力；第三部分是泵排量执行机构，伺服活塞大小腔压力的变化会导致活塞的左右移动，从而带动连杆的左右移动，进而改变泵的斜盘倾角，从而引起泵的排量变化。

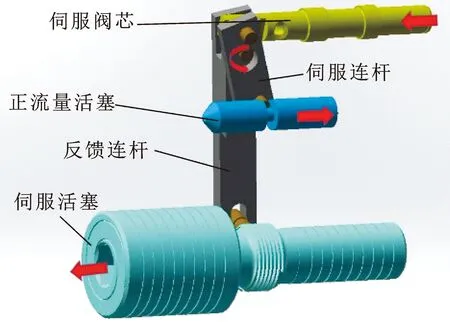
图1 正流量变量泵系统排量主要调节机构

第一部分电流位移转换机构，考虑到正流量活塞的响应速度要远远滞后于电磁阀，故将第一部分视为比例环节，作用在正流量活塞上的液压力为

F∑=ki·i=kΔx

(1)

式中：Δx为正流量活塞位移，mm；i为电磁比例减压阀输入电流，mA；ki、k为比例系数。

第二部分是伺服变量机构，工作原理如图2所示。假设阀为理想的三通滑阀，忽略阀内流量变化的时间和阀内的所有泄漏。对控制腔应用流量连续方程[15]，得：

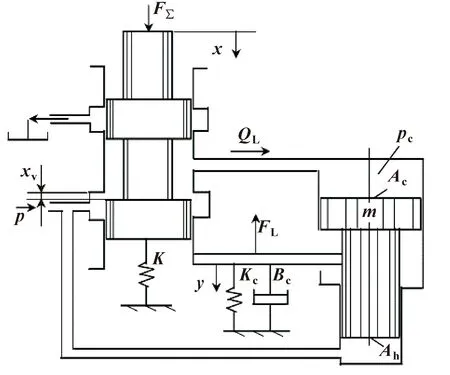
图2 变量泵排量调节结构[15]

QL=Kqxv-Kcpc

(2)

(3)

式中：Kq为伺服阀流量增益；Kc为伺服阀流量压力系数；xv为伺服阀阀芯开口量，mm；Ac为变量活塞大端面积，m2；V0为控制腔容积，cm2；βe为油液体积弹性模量；x为变量机构输出位移，mm。

活塞和负载受力平衡方程[15]：

(4)

式中：Ah为活塞小端面积，m2；p0为泵出口压力，MPa；FL为伺服活塞负载力，N；m为伺服活塞质量，kg；Bc为黏阻系数；Kc为弹簧刚度。

对式(2)—(4)进行拉氏变换：

QL=AcsX+V0/βesPc

(5)

PcAc-P0Ah+FL=ms2X+BcsX+KcX

(6)

求出正流量活塞对伺服阀芯位移的传递函数：

X=

(7)

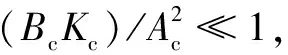
(8)

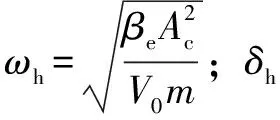
伺服活塞对伺服阀芯位移的传递函数为

(9)

第三部分是泵排量执行机构：伺服活塞阀芯位移为x时，对应的斜盘倾角为α，则变量泵的排量为

α=K1x

(10)

qv=Kvtanα

(11)

变量泵的流量为

Q=wqv

(12)

式中：w为发动机转速。

上述推导过程，忽略泄漏以及摩擦等非线性因素，可推导出整个系统为一个近似的三阶系统。

2 系统辨识与建模

正流量实验台由挖掘机川崎主控制器(型号为KC-ESS-20A-049)、日本川崎的K7V125DTP1D9R-0E05-1AV正流量电控变量泵、S-YY-008泵马达综合实验台、挖掘机川崎主控制器(型号为KC-ESS-20A-049)、奥地利DEWESOFT公司的DEWE-43A数据采集仪和深圳零欧智能工业有限公司的31JH-70-35.030流量传感器等组成。实验原理与实验台架结构示意如图3所示。

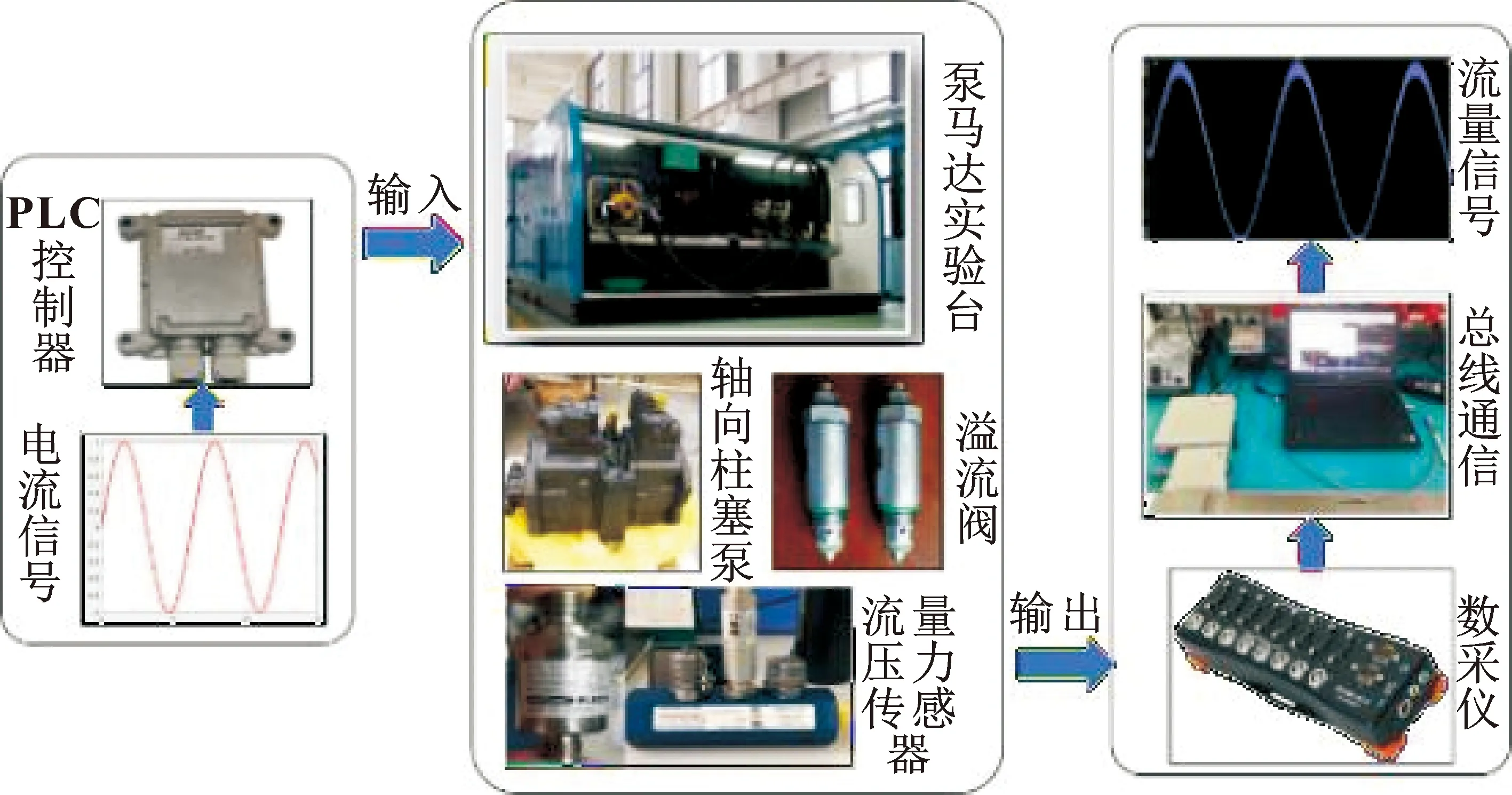
图3 正流量实验台架结构

通过S-YY-008泵马达综合实验台进行正流量变量泵实验，向PLC控制器输入正弦电流信号调节变量泵排量；在变量泵出口处连接流量计，并借助数据采集仪测得输出流量，最后通过总线通信，将输出流量信号显示在计算机显示器中。

在额定工况下，以不同频率的正弦电流信号作为液压泵的激励信号，通过流量传感器反馈不同激励信号下的液压泵流量，得到开环系统的频率特性数据。由于高阶的系统传递函数模型会增加控制器的复杂度，利用最小二乘法，应用系统辨识的方法得到低阶的开环传递函数：

(13)

对于辨识得到的数学模型，可以应用MATLAB/Simulink对系统进行正弦的仿真。仿真结果和实验结果的对比如图4所示。

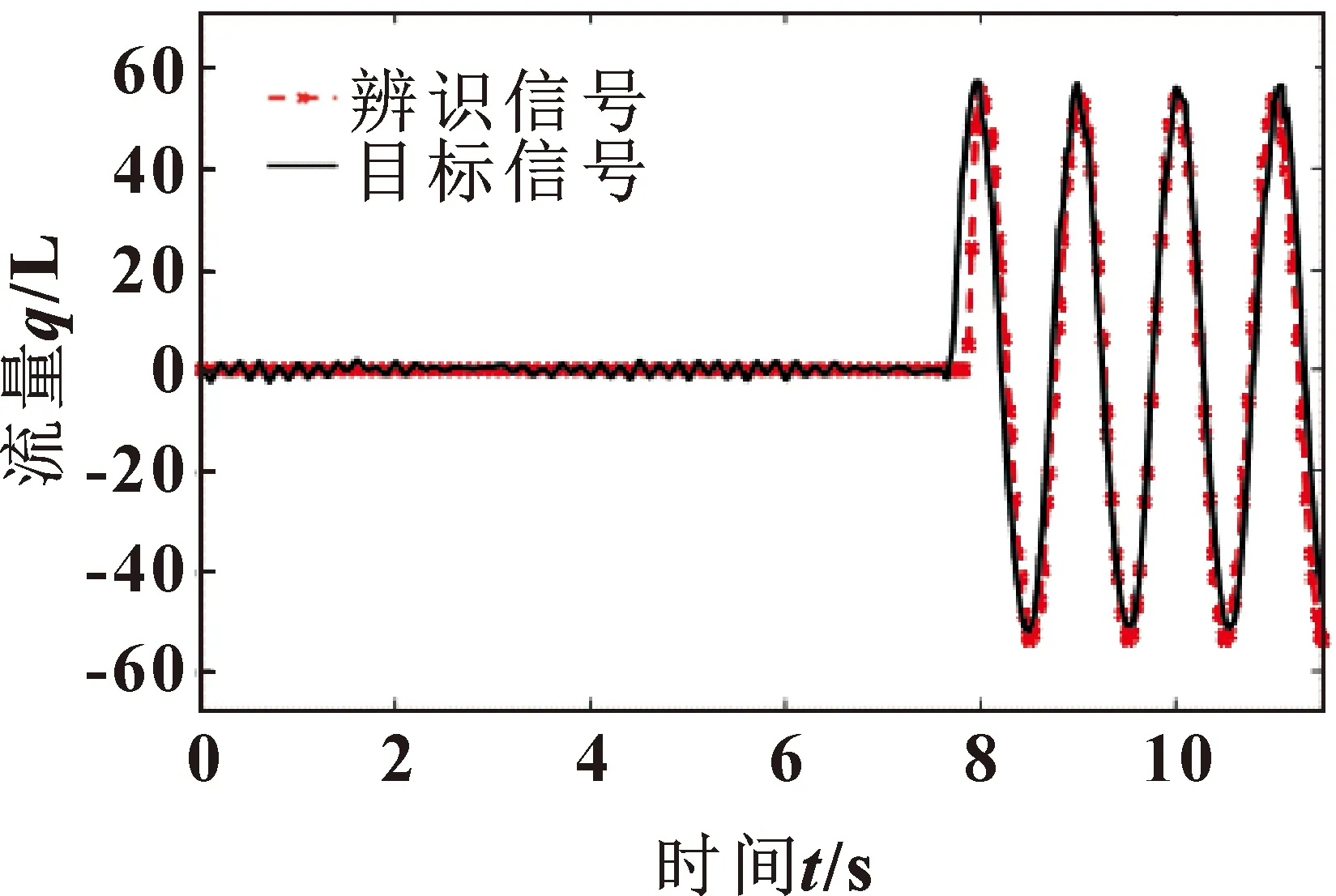
图4 仿真结果与实验结果的对比

由图4可知：系统的仿真结果和实验结果基本相同，这也就证实了式(13)作为系统的数学模型实验的正确性。

3 滑模自适应控制器的设计

正流量变量泵在工作过程中，实际存在高频的部分以及工作状态下的自激状态可能对正流量变量泵系统产生一定的影响，另外液压缸中的容积、电磁比例阀二次压力等因素都会造成传递函数的变化，活塞和阀在运动过程中的摩擦阻力、泄漏等干扰因素都可能导致传递函数的参数发生变化。然而当系统的非线性、时变性以及复杂干扰较强时，传统的PID控制算法难以满足精确的流量控制要求，系统的跟踪响应适应性较差。考虑到正流量变量泵应用场合中非线性因素和扰动因素，将滑模控制和RBF神经网络最小参数学习法的思想引入到正流量变量泵伺服流量闭环控制，设计基于神经网络最小参数学习法的正流量变量泵滑模自适应控制器，该控制器总体结构如图5所示。首先设计滑模自适应控制器，用于改善控制系统的控制性能，使得系统拥有更好的跟踪响应，接着通过Lyapunov方程证明系统的稳定性。

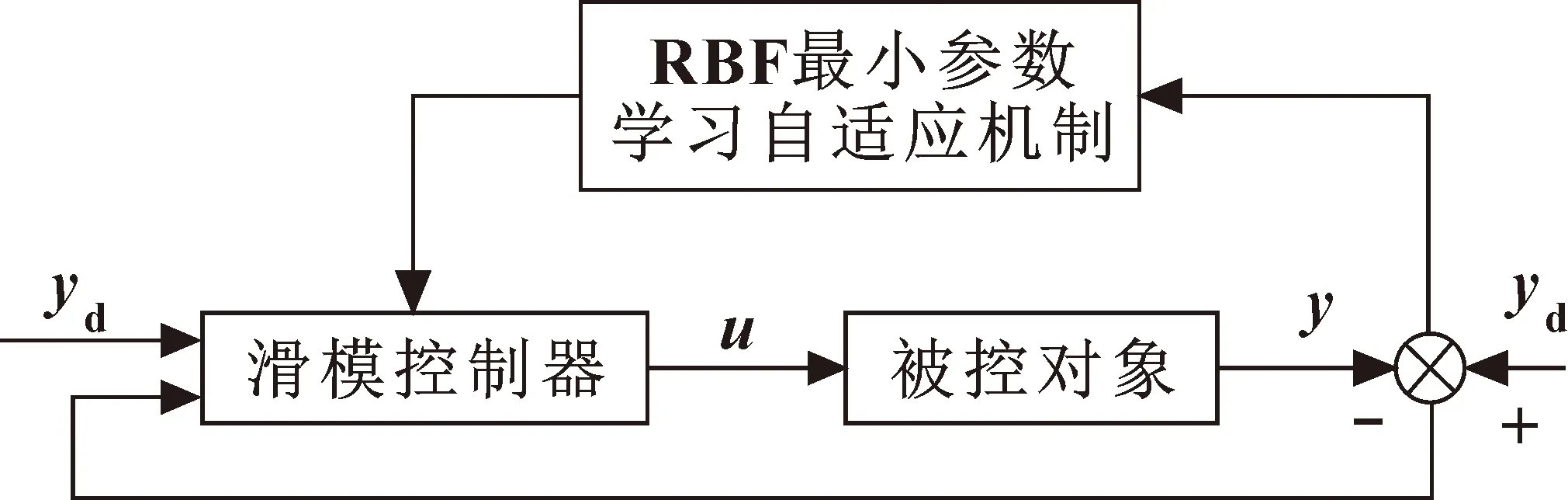
图5 基于RBF最小参数学习法的滑模自适应控制闭环系统

3.1 基于RBF最小参数学习法的滑模自适应控制器的设计

将正流量变量泵系统的动态方程描述为

其中：f(x)为未知非线性函数；g为已知常数；u∈R和y=θ∈R分别为系统的输入和输出；d(t)为外加干扰，|d(t)|≤D，其中令不确定项确定为f=f(x)+d(t)。

设位置指令为θd，令e=θ-θd，设计切换函数为

s=e′+ce

(14)

其中：c>0。

于是

(15)

利用RBF神经网络的最佳逼近性质对不确定项进行自适应逼近。RBF网络算法为

f=WTh(x)+ε

其中：x为神经网络的输入信号；j为神经网络隐含层节点的个数；h=[h1,h2,…,hm]T为高斯基函数的输出；W为理想神经网络权值；ε为神经网络逼近误差，|ε|≤εN。

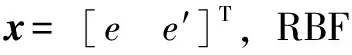
(16)

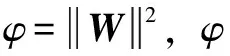
设计控制律为

(17)

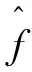
将控制律u代入式(15)，得

(18)

设计自适应率为

(19)

其中：κ>0。

3.2 稳定性分析

定义Lyapunov函数为

其中，γ>0。

对L求导，并将式(17)和式(18)代入，得

(20)

于是

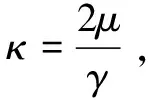
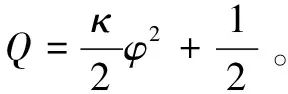
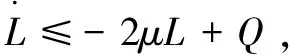
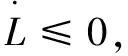
推到过程中用到2个结论：

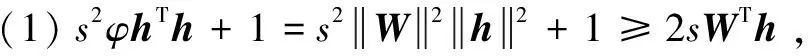
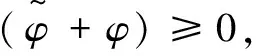
4 仿真实验

4.1 仿真实验参数设置

为了验证控制算法的切实性，在MATLAB/Simulink环境下，对RBF最小参数学习法的SMC算法进行仿真。具体仿真实验参数设置如下：

被控对象取正流量变量泵系统，其动态方程如下：

(21)

其中：f(·)=-51.47x2-1 486x1+d(t)，g=802.21，x1和x2分别为目标值和目标值的一阶导数；u为控制输入。

取x1=θ，目标流量指令为θd=30sin(2πt)，干扰取d(t)=10sin(2πt)。电控正流量泵初始状态是[π/60,0]，控制律取式(18)，自适应率取式(20)，自适应参数取γ=150。在滑模函数中，取c=100，η=98。

4.2 仿真实验结果分析

为了便于分析，在正弦指令下获得基于RBF最小参数学习法的SMC控制与PID控制和模糊PID控制系统的对比跟踪响应。仿真结果如图6和图7所示。

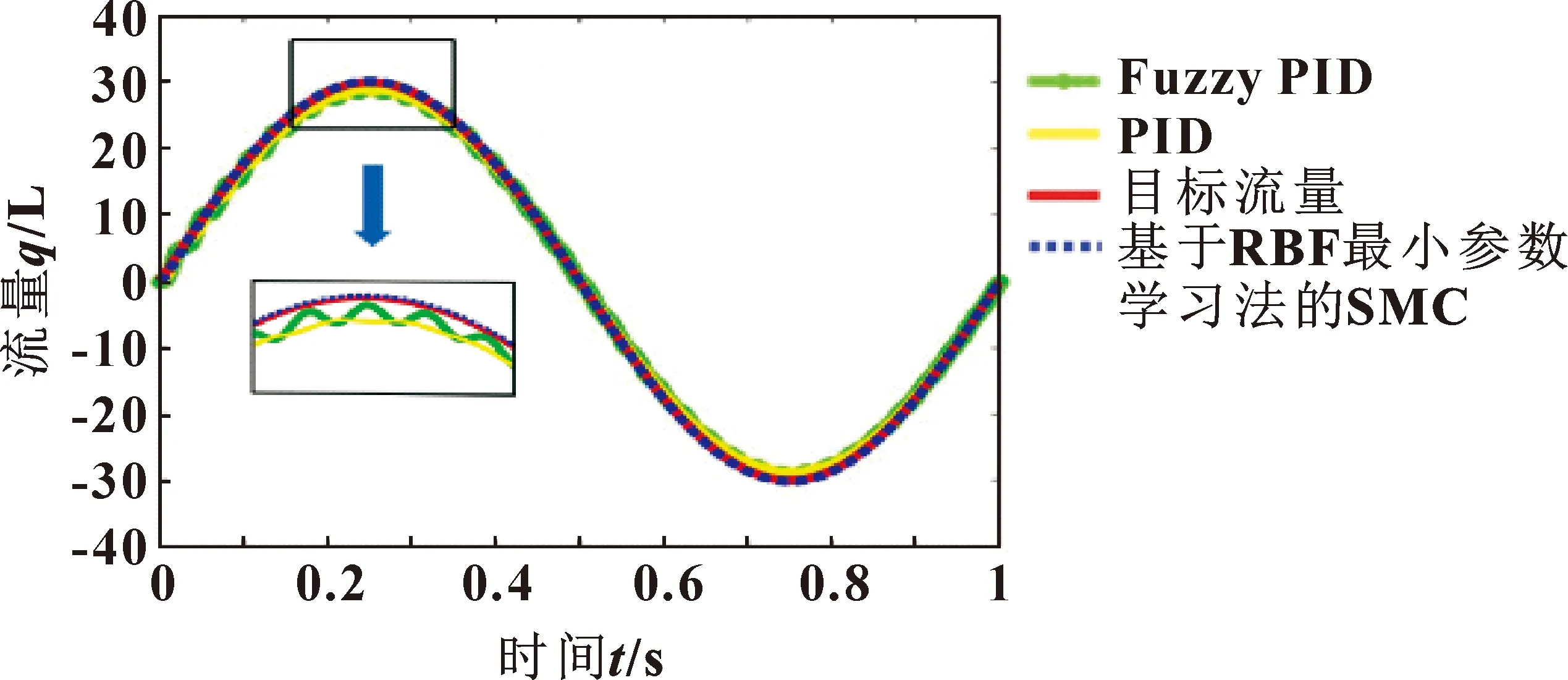
图6 电控正流量变量泵的流量跟踪曲线

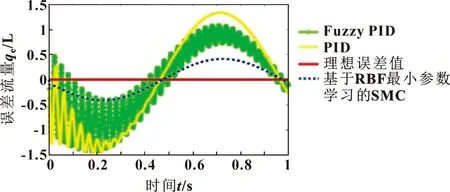
图7 电控正流量变量泵的流量跟踪误差

如图6所示：3个控制算法基本上都实现了对目标流量的跟踪性，但是相比之下，基于神经网络最小参数学习法的滑模控制器跟随特性最好且波动最小。

综合仿真结果如图7和表1可知：与传统PID控制器和模糊PID控制器相比，基于RBF最小参数学习的自适应SMC控制器的目标流量跟踪的平均跟踪误差为0.19，最大误差为0.42，明显低于其他2种控制策略。

表1 流量误差比较

同时，文中又对比不同频率输入目标信号对应的输出信号，仿真实验结果如图8所示：基于RBF最小参数学习法的滑模控制自适应能较好地适应输入目标信号的变化，具有较好的跟踪性和鲁棒性。

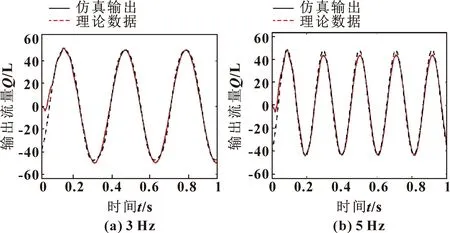
图8 不同频率输入目标信号与滑模自适应输出信号对比

5 结论

(1)文中考虑了模型的不确定性和负载扰动等非线性因素，验证了基于RBF最小参数学习法的滑模自适应控制算法应用于正流量变量泵电液伺服系统流量控制的有效性。采用神经网络最小参数学习法对模型的不确定性和负载扰动进行逼近和补偿，自适应机制通过参数的估计代替神经网络权值的调整。在滑模中引入非线性项和干扰项，设计了自适应滑模控制器。

(2)通过MATLAB/Simulink联合仿真平台，进行了正流量变量泵电液伺服系统的正弦信号响应的系统辨识实验，并对所设计的控制器与传统PID控制器和模糊PID控制器的性能进行了比较。与传统PID控制器和模糊PID控制器相比，基于RBF最小参数学习的自适应滑模控制器的目标流量跟踪相对于PID控制器的平均跟踪误差降低了75%，最大误差降低了68%。经仿真结果验证，所设计的控制器对模型不确定性和负载扰动具有较强的鲁棒性，并且对正弦目标信号具有较好的跟踪性。