模块化管道清洁机器人设计与通过性分析

宋进，张晓龙，李俊杰，黄旷，刘杰，武龙飞

(昆明理工大学机电工程学院，云南昆明 650093)

0 前言

石油、天然气作为重要的能源，其需求逐年增加。在石油、天然气的运输方面，管道因成本费用较低、可连续作业、便于管理和控制等优点逐渐成为主要的运输方式[1]。与人工相比，管道机器人可以在不同管径的管道内部行走，搭载工作设备进行相应清洁维护等工作，具有更高的安全性与适应性。二十世纪五十年代起管道机器人开始兴起，经过几十年的发展，国内外的研究取得了一系列成果。依据机器人的机械结构形式和运动方式的不同可划分为流体式、轮式、履带式、爬行式、蠕动式、螺旋式和仿生式等[2-4]。其中较为典型的有：国外学者最先研制的一种流体式管道作业装置PIG(Pipeline Inspection Gauge)[5-6]来清理和检测管道；日本中央大学研制的蚯蚓蠕动式管道机器人[7]；哈尔滨工业大学邓宗全等[8]研制的六驱动轮相互独立的轮式管道机器人；西南石油大学刘清友[9]研发的主动螺旋式管道机器人，哈尔滨工业大学李庆凯等[10-11]研制的三轴差速式管道机器人。

本文作者结合国内外已有管道机器人的特点，就管道机器人普遍存在的变径不够柔性化、通过性与适应性差等问题，设计一种可以进行柔性变径的模块化履带驱动管道清洁机器人，可在不同情况对机器人进行改变。首先对行走机构及管道机器人的管径适应性进行力学分析；然后分析管道机器人在直管、弯管中的通过性及越障能力；最后在ADAMS中分析机器人的运动状态。

1 机器人整体结构

此机器人主要工作在300～450 mm直径的小型油气运输管道中，由于这类管道空间所限，人无法进入，需要利用管道机器人搭载作业设备进入其中完成清洁任务。因此机器人需要在行走时有足够的驱动力、在转向时有良好的过弯性以及整体的稳定性。设计的履带式清洁管道机器人三维模型如图1所示，由摄像照明、行走变径、先清洁、后清洁以及控制几部分组成。摄像照明观察污垢情况，行走变径负责机器人的前进和管径适应；前后清洁部分依次清理污垢，控制部分则是控制修改其他模块的参数。各部分之间通过连接件进行固定、连接，可对各个部分采取不同的装配方式以达到不同的需求。行走变径部分为履带驱动，并在履带支架上增加1-2个可调节的惰轮来实现张紧的功能，压缩弹簧结合变径杆使得变径过程柔性化。

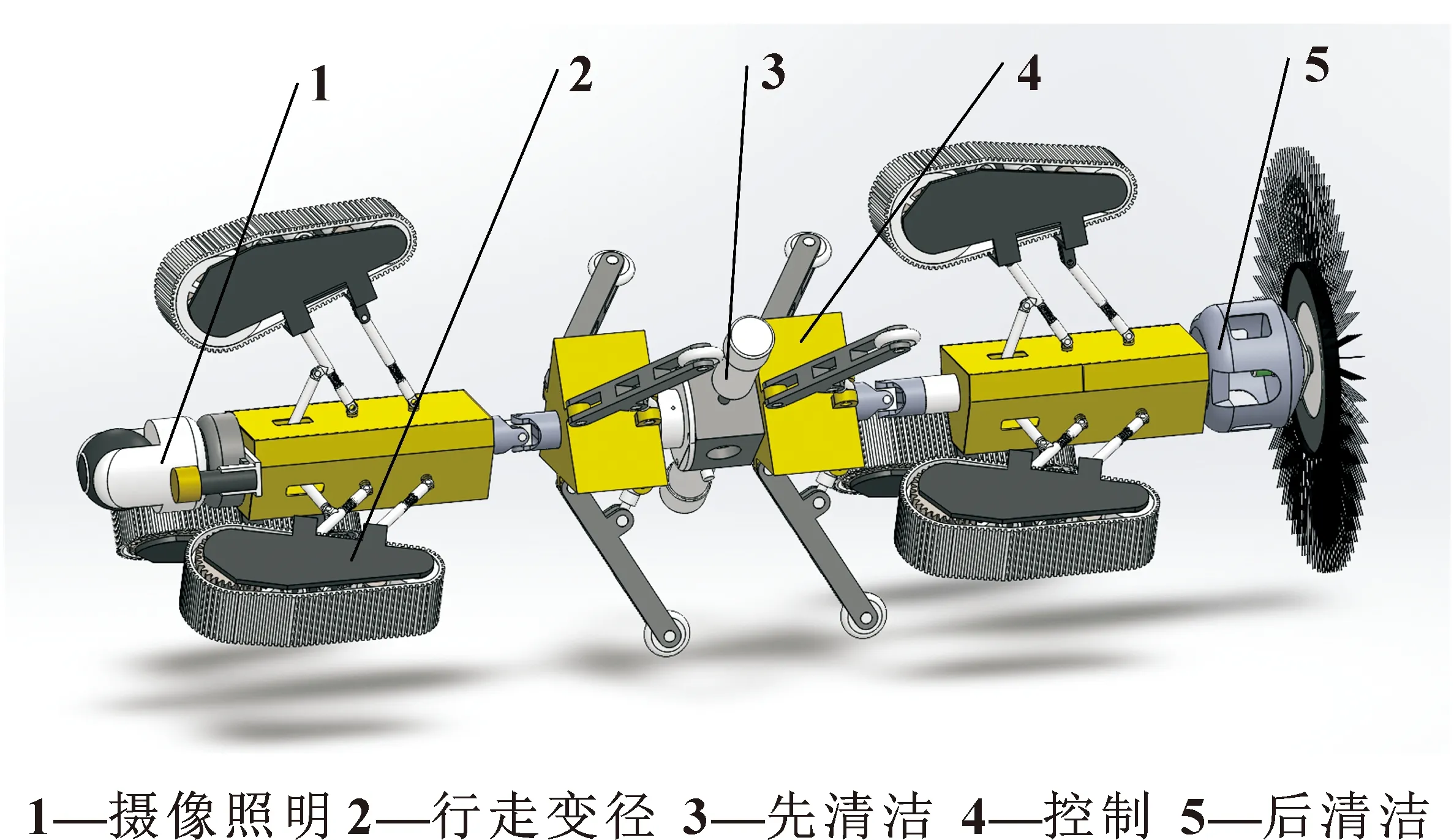
图1 管道机器人模型

清洁工作由先清洁部分上所搭载的激光清洗头对杂质进行第一次清洁，随后，后清洁部分通过清洁工具盘刷与管道内壁接触，然后通过电机驱动盘刷对管道内壁进行二次清洁。后清洁部分如图2所示。控制部分是对摄像照明、清洁、行走变径等过程进行相应的参数控制。

图2 管道机器人后清洁机构

2 行走机构力学分析

管道机器人工作有水平管道和竖直管道。当管道机器人在水平直管中行走时，可忽略行走机构支撑的弹性阻力和履带轮转速失配导致的电机附加阻力。图3(a)为管道机器人行走机构在水平管道行走的受力示意，图3(b)为垂直管道行走的受力示意。其主要参数有：管道内壁的支持力∑Ni，履带和管道内壁摩擦因数为μ；所受滚动摩擦力总记为Fg；驱动轮半径为r；履带传动效率为η1；行走机构齿轮组传动效率为η2；电机扭矩输出为Me。

图3 管道机器人行走机构受力

可得电机转矩最少为

(1)

管道机器人在通过弯道时，需要考虑行走机构的附加阻力，该附加阻力与变径机构弹簧的刚度以及履带驱动轮与管壁之间的距离相关。在实际作业的油气管道内，通常会存在油料残留物或管壁被腐蚀后产生的黏性液体，使得行走履带和管道内壁摩擦力减小。当行走机构驱动电机功率足够时，若履带轮与管道内壁滑动，此时行走机构提供最大牵引力为F=μ∑Ni，管道机器人牵引力受摩擦因数影响。

3 管径适应性力学分析

通过驱动电机旋转带动丝杠，进而带动整个行走机构运动，以履带轮的升降达到管径适应的目的。文中所设计的管道机器人6个驱动履带均有动力，前后驱动模块呈对称分布，管道机器人3个履带轮之间两两呈120°夹角，所以研究驱动履带运动力学时只需要任选其中一组。如图4、5所示：γ为管道机器人的姿态角；θ是驱动履带轮与管壁的接触点与管道中心的连线和管道机器人中线的夹角，该角对应的弧长记作s；摩擦因数为μ；φ为履带轮和机器人中心线的夹角，φ=60°。

图4 管道机器人管径适应机构示意

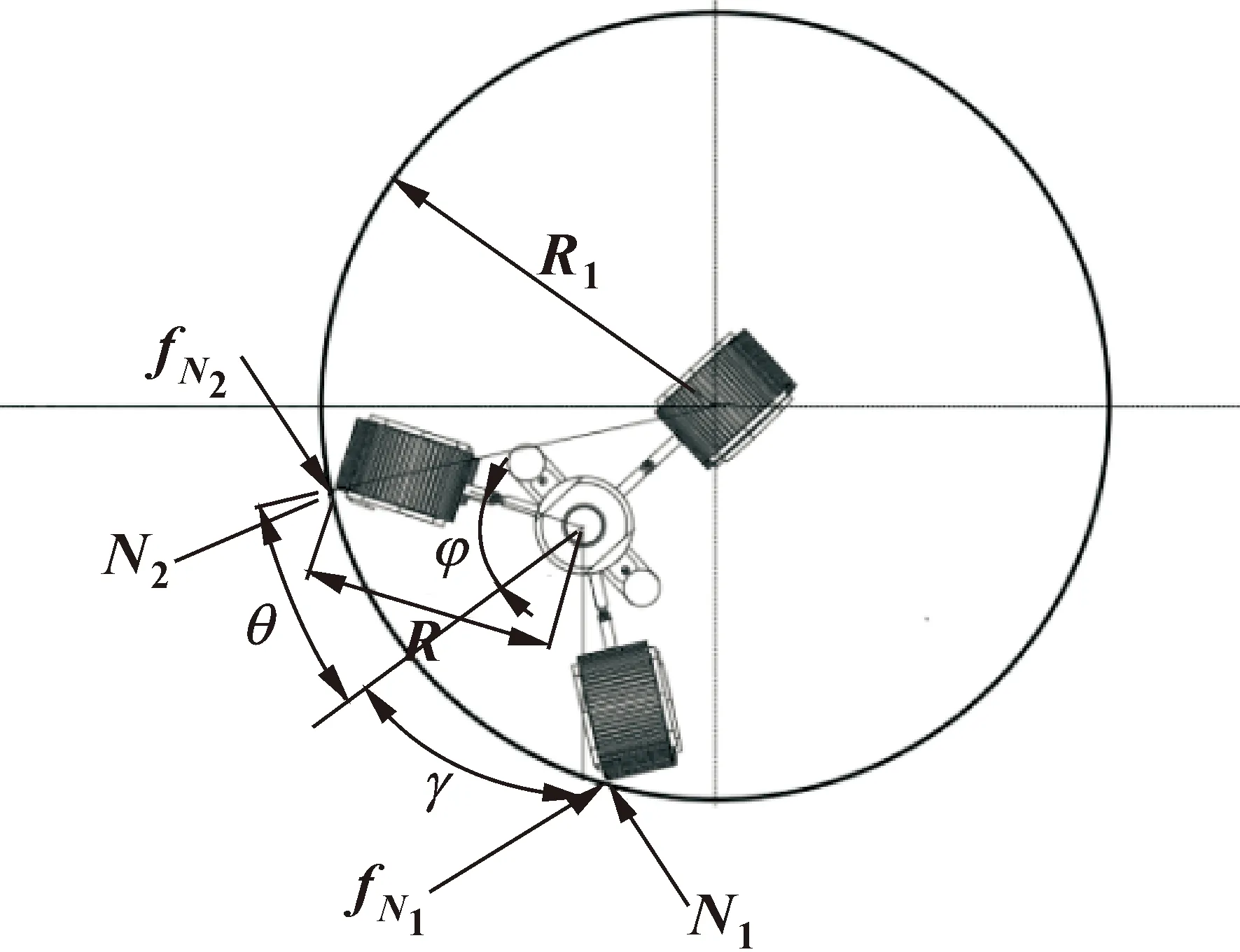
图5 管道机器人管径适应机构径向视图

管道机器人在适应管径变径时，机器人的中心和管道中心的位置有偏差，在变径机构调节的过程中，管道机器人需要克服履带轮和管道内壁之间的摩擦力，对这一过程的力学进行建模和分析。

由管道机器人几何关系图可得：

(2)

对式(2)两边进行微分：

(3)

由图中的几何关系可得：

(4)

代入式(3)整理后可得：

(5)

化简式(5)可得：

(6)

机器人工作油气管道坡度为∂，自身重力记为mg，管道对履带轮的支撑力之和记作∑N，根据虚功原理有：

(7)

联立上式化简得：

(8)

由虚位移原理可得变径机构的丝杠螺母运动副输出的转矩T和传动效率的关系：

Fδs+Tδφη=0

(9)

整理式(9)得：

T=

(10)

式中：P为丝杠导程；φ是丝杠和螺母之间的转角。可知变径机构在工作时所需的推力F与丝杠电机输出扭矩T受α、β值影响，即受连杆AB和OC与水平方向夹角大小的影响；当工作管道半径R1一定时，α、β值的大小与丝杠螺母副的推力F以及丝杠驱动电机的输出扭矩T成反比，即在机器人变径适应管道α、β增大的过程中，丝杠驱动电机的输出扭矩是逐渐减小的，反之α、β变小的过程，电机输出扭矩T是逐渐增大的。

4 弯管几何约束分析

机器人L形管道通过情况如图6所示，为了方便研究将机器人近似看做一个圆柱体，主要参数有机器人长度L、直径d、所通过管道管径D、弯道曲率半径为R、弯道的旋转角度α，L形管道α一般取值为90°。机器人在L形弯道通过时，有2种极限情况需要考虑：机器人两端在弯管的直边部分卡住，如图6(a)所示；机器人两端在管道内部卡住，如图6(b)所示。

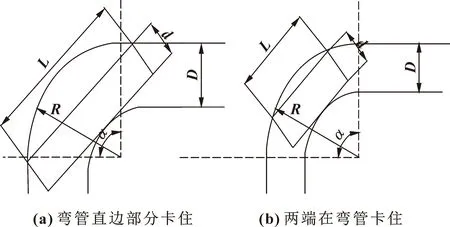
图6 管道机器人在弯管卡住的2种情况

图6(a)中机器人2个端面卡在L形弯道旁边直管部分，处于第一种极限位置。该极限位置机器人直径和弯道曲率半径以及管道直径满足下式：

(11)

图6(b)中机器人2个端面卡在弯道内部的旋转管道部分，处于第二种极限位置。该极限位置机器人直径和弯道曲率半径以及管道直径满足下式：

(12)

5 机器人管道通过性分析

5.1 机器人管道运动分析

当机器人适应了管径后，需要分析它在管道中的运动。在直管内，建立机器人在水平管道运行时的坐标系如图7所示。确定参考坐标系o-xyz；建立机器人运动坐标系E-abc，该坐标系跟随机器人运动，在机器人中心轴线上确定动坐标系原点E，该点到任一履带轮距离相等，Eb轴方向为竖直方向，通过右手法则确定Ec方向。

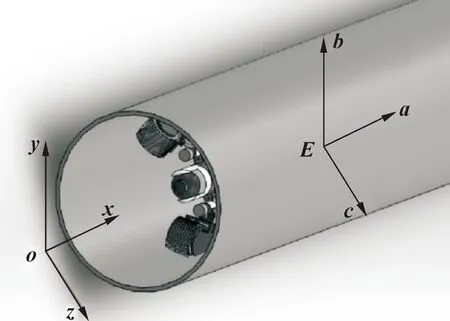
图7 管道机器人管道运动坐标系

管道机器人在管道中行走工作时受力[12]为

F=3Fd+G1+G2+∑Ni+∑Ff

(13)

当机器人在管道中行走时合力矩为

M=3Md+M1+M2+∑Mi+∑Mf

(14)

式中：F为履带驱动轮所提供的驱动力；G1是机器人的自身重力；G2为携带摄像和清洁模块所需要的力；∑Ni为驱动履带和管道内壁封闭力的合力；∑Ff为总摩擦力的合力。Md、M1、M2、∑Mi、∑Mf分别为Fd、G1、G2、∑Ni、∑Ff产生的力矩。

对管道机器人分析时将它看做一个整体，设机器人质心为H，质心在动坐标系位置为(xH，yH，zH)。H到该坐标系原点的矢量距离RH，动坐标系原点E相对于参考坐标系o-xyz的相对速度v在abc方向上的分量记作va、vb、vc。E相对于参考坐标系相对角速度ω在abc方向上的分量记作ωa、ωb、ωc。质心H的速度矢量表达式为

vH=v+ω×RH

(15)

对式(15)两边求导可得质心的加速度表达式

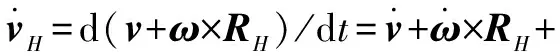
(16)

vH=v

(17)

管道机器人总质量记作m，设转动惯量为I，可以得出机器人的质心H的动力学方程：

mvH=mv=F

(18)

油气管道铺设中弯道多为L形弯管，主要研究文中设计机器人在L形垂直弯道行走时运动分析。在垂直弯管中行走主要分为过渡和旋转2个阶段，即机器人一端先进入管道另一端还在直管和机器人完全进入弯道2个阶段[13]。

(1)过渡阶段分析

机器人在垂直管道中运动时，第一个阶段是过渡阶段。过渡阶段从管道机器人前端进入管道开始到后端完全进入弯道内，以及离开管道时前端从弯管进入直管到后端完全离开弯管进入直管。该阶段机器人做平面运动，由于文中设计机器人对称分布，分析机器人在弯道内的运动时只需选取一段履带轮即可，具体如图8所示。

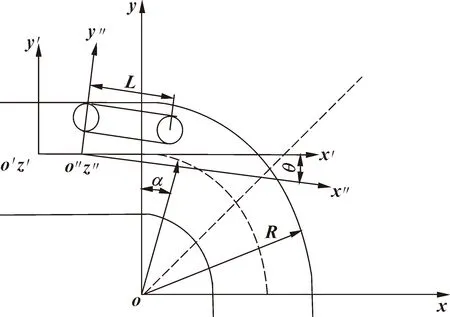
图8 管道机器人过渡阶段运动分析

图中o′-x′y′z′为过渡坐标系，o″-x″y″z″为动坐标系，该坐标系建立在机器人上，即为机器人的动坐标系。坐标系o′-x′y′z′旋转θ后得到坐标系o″-x″y″z″。机器人履带轮前后轮中心距为L，管道的曲率半径为R；入弯角为α，图5中γ为管道机器人的姿态角。过渡阶段机器人做平面运动，这一阶段管道机器人前后履带轮与管道接触的位置坐标[14]可表示为

(19)

式中：矩阵F″W、R″W分别表示机器人驱动前、后履带轮与通过弯管内壁的接触点在坐标系o″-x″y″z″中的坐标。

图8中o-xyz为管道的坐标系，该坐标系是固定不变的，将机器人坐标系通过平移和旋转可以得到坐标系o-xyz。过渡阶段平移向量：

(20)

有绕轴z″、旋转角度为-θ的旋转矩阵：

(21)

于是管道坐标系上机器人前后履带轮和管道内壁接触位置坐标为

(22)

联立式(18)—(22)可得：

(23)

在矩阵FW中：

xf1=Rα-L+Lcγ+0.5Dsγsθ;

yf1=R-Lsθ+0.5Dsγcθ;

xf2=Rα-L+Lcθ+0.5Ds(120°+γ)sθ;

yf2=R-Lsθ+0.5Ds(120°+γ)cθ;

xf3=Rα-L+Lcθ+0.5Ds(240°+γ)sθ;

yf3=R-Lsθ+0.5Ds(240°+γ)cθ

在矩阵RW中：

xf1=Rα-L+0.5Dsγsθ;

yf1=R+0.5Dsγsθ;

xf2=Rα-L+0.5s(120°+γ)sθ;

yf2=R+0.5Ds(120°+γ)cθ;

xf3=Rα-L+0.5s(240°+γ)sθ;

yf3=R+0.5Ds(240°+γ)cθ

式中：cγ=cosγ；sγ=sinγ。

入弯过渡阶段的旋转角α与弯道曲率半径R和机器人长度L相关，旋转角α决定θ角的大小，于是有：

α=0～2arcsin[L/(2R)]；

(24)

(2)旋转阶段分析

图9所示为机器人在完全进入弯管时的旋转阶段运动分析。图中对管道机器人一组履带轮行走分析，过渡坐标系o′-x′y′z′旋转(-φ-α/2)角度得到动坐标系o″-x″y″z″。管道机器人旋转阶段是绕曲率中心轴oz进行旋转运动，前后履带轮轨迹相同，于是有：

图9 管道机器人旋转阶段运动分析

(25)

机器人旋转时平移矩阵：

(26)

于是得到机器人旋转表达式：

R(z″，(-φ-α/2))=

(27)

联立式(25)—(27)可得：

FW=RW=

(28)

式(28)中：

xf1=Rsφ+0.5Dsγs(φ+α/2)；

yf1=Rcφ+0.5Dsγc(φ+α/2)；

xf2=Rsφ+0.5Ds(120°+γ)s(φ+α/2)；

yf2=Rcφ+0.5Ds(120°+γ)c(φ+α/2)；

xf3=Rsφ+0.5Ds(240°+γ)s(φ+α/2)；

yf3=Rcφ+0.5Ds(240°+γ)c(φ+α/2)；

α=arcsin[L/(2R)]

φ为旋转阶段机器人绕曲率中心的旋角，取值范围为：φ=0～(90°-α)，式(23)(28)描述了管道机器人通过L形管道时履带轮和管道内壁可能接触点的运动轨迹方程。

油气管道随着投入使用的时间增加，会有不同程度和形式的形变，以及管道在焊接过程中存在焊缝等影响管道平整的因素[15]。所以管道机器人在设计时需要具备一定的越障能力，即机器人能顺利通过管道内凸起的障碍。履带轮式行走机构越障能力和最小半径的轮相关[16]，设障碍物是规则的方形台阶，文中选取机器人较小履带轮进行分析，如图10所示，根据静力学平衡方程有：

图10 管道机器人越障轮受力

(29)

式中：α为越障角；N1为越障时障碍台阶对轮的反作用力；N2、N3为管道壁对另外2个驱动轮的反作用力；μ为另外两驱动轮和管道内壁间的摩擦因数；μ1为越障驱动轮和障碍台阶间的摩擦因数。

联立式(29)消去N1可得：

(30)

如图10所示，设障碍高为h，根据几何关系有：

(31)

联立式(31)可得：

(32)

根据式(32)可知：石油管道机器人可越过障碍物的最大高度与机器人最小驱动履带轮的半径以及摩擦因数相关。文中设计最小驱动履带轮半径为25 mm，驱动履带轮和管壁之间摩擦因数取0.3，障碍物和驱动履带轮之间摩擦因数取0.2，代入式(32)可计算出机器人最大越障高度为7.8 mm。结合变径机构的设计，可知越障高度满足技术要求。

综上可知，管道机器人通过障碍能力与最小驱动轮半径相关，同时管道与驱动轮之间以及障碍物和驱动轮之间的摩擦因数也影响障碍通过能力。管道机器人履带轮半径越大，障碍通过性能越强，摩擦因数高时通过性能也强。

5.2 机器人管道运动仿真分析

为了验证所设计的管道机器人的合理性，文中使用SolidWorks建立管道机器人模型，然后导入ADAMS进行仿真分析和验证。为了方便ADAMS模型的建立和分析，文中将行走机构以驱动轮替代履带式进行仿真，导入模型后，如图11所示。设置工作栅格、定义材料属性、设置重力加速度、创建相应约束以及接触，随即创建管径适应机构弹簧、创建管道机器人驱动轮进行驱动，最后得到管道机器人在L形弯管通过性的仿真结果。

图11 管道机器人虚拟样机模型

此次仿真实验目的是验证所设计管道机器人能否顺利通过L形弯管。对管道机器人在一段L形弯管中的运动进行了仿真，并得出了行走机构和机器人机身的运动轨迹。图12所示为管道机器人正通过L形管道。

图12 管道机器人通过L形弯管示意

仿真实验中L形管道设置曲率半径为1.5D，行走管道的动摩擦因数设置为0.1，静摩擦因数设置为0.3。在驱动轮上添加旋转运动，在函数(时间)处修改为180d*time，表示驱动轮每秒旋转180°，完成有关驱动轮驱动的创建。分别得出行走过程中驱动轮过弯以及在x、z方向上的速度关系曲线，如图13所示。

图13 管道机器人通过L形弯管速度曲线

图13(a)为管道机器人通过曲率半径为1.5D的L形弯管过程中，3个后行走机构驱动轮之间的速度关系。可知：当机器人从直管部分进入弯道时，即进入过渡阶段。在过渡阶段，行走机构驱动轮速度不一样，外侧驱动轮速度大于内侧驱动轮，处于中间位置的驱动轮速度也介于内外轮之间。管道机器人通过弯道后，各个行走机构的驱动轮速度相同，此时进入另一段直管部分。由于机器人行走机构设置有弹簧且轨迹接触点随着行走不断变换，各轮的速度存在一定波动，符合管道机器人运动规律以及运动规划。

图13(b)(c)为管道机器人通过L形弯管过程中，前、后模块的行走机构3个驱动轮在x、z方向上的速度曲线。可知：在0～4 s，当管道机器人前后模块都在直管阶段时，前、后行走机构的驱动轮在x方向上速度均为0，而在z方向上速度为初始速度。4 s时机器人开始进入弯道，前、后模块行走速度开始存在差异。前部模块行走机构进入弯道时，其驱动轮在z方向上速度减小，同时在x方向上速度增大，又由于通过弯道时3个驱动轮存在差速，所以其速度曲线不完全重合。20 s时前部模块顺利通过弯道后，其在z方向上的速度降为0，在x方向上速度恒定。当后部模块行走机构进入弯道时，重复前述动作。

建立管道机器人虚拟样机和曲率半径为1.5D的L形弯管，得出了行走过程x、z方向上的速度关系曲线，验证了管道机器人的通过性。通过仿真实验结果验证了管道机器人机构设计的合理性和L形弯管的通过性，同时也与上述过弯运动规划相互印证。

6 结论

文中设计了一种具有观察、2次清洁功能的管道机器人，简要叙述了各个组成部分的功能。对行走机构进行力学分析，对机器人能否适应不同管径进行几何、力学分析，得到相关条件；最后通过运动分析，进行相关参数的验证。作者在几何、力、运动方面验证了所设计的管道机器人的合理性，为接下来物理样机的制作以及进一步的实验验证提供了支撑。