铝电解槽热场和流场的测试分析和数值模拟

王 怡, 邓胜祥

(1.上海工程技术大学 机械与汽车工程学院能源与动力工程系, 上海 201620;2.上海工程技术大学 新能源与节能新技术研究所, 上海 201620)

如今铝电解槽工业的槽电流强度不断增加,逐渐发展到300 kA、400 kA、500 kA等槽型[1]。铝电解槽具有几何形状复杂、体积庞大等特点,采用数值模拟的方法可以降低铝电解槽测试工作的难度,提高测试效率,同时可依据数值模拟结果提出铝电解槽优化方案,为生产提供指导[2-3]。

铝电解槽各个物理场互相作用、互相影响。铝电解槽内热场分布的情况是槽工况表现的重要特征,合理的热场状态有利于槽膛内形稳定,使炉帮形成状态良好,不易发生破损;同时,热损失是衡量整个电解槽能量平衡及能量利用率的重要指标[4]。铝电解槽内铝液和电解质运动是铝电解槽稳定性的一个很重要的因素[5-9],一个热场稳定的电解槽可以增加铝电解的产量和电流效率,从而延长槽寿命[10-12]。

前人对铝电解槽热场和流场等物理场进行了研究,周乃君等[13]模拟156 kA铝电解槽并应用实测数据进行验证。肖忠良等[14]探究240 kA铝电解槽改变电解槽工艺参数对槽内温度的影响;刘妮[15]基于FLUENT研究320 kA铝电解槽的流场仿真;刘正华[16]以175 kA铝电解槽为模型,在铝电解槽电磁流耦合计算模型的基础上对熔体流场进行了稳态计算,分析研究不同工况条件对铝电解槽熔体流动的影响;刘冠祚等[17]通过电磁流顺序耦合,在ANSYS平台上数值模拟仿真300 kA铝电解槽,得到其流场分布情况。目前对于400 kA及以上铝电解槽研究内容较少,本文应用COMSOL软件分析研究400 kA铝电解槽物理场状态,对某厂家的400 kA铝电解槽的表面及熔体温度等进行热场测试。采用铁棒溶蚀法[18-22]对某厂家的400 kA铝电解槽进行铝液层流场测试,并运用COMSOL三维仿真软件数值模拟热场切片模型和流场整槽模型,探讨了铝电解槽的热场温度分布状况和铝液层运动流向的变化,验证铝电解槽的设计结果,进而为铝工业生产发展提供技术支持和理论依据。

1 铝电解槽数学模型

1.1 热场数学模型

1.1.1控制方程

电解槽温度在短时间内是稳定的,可认为是稳态,适用拉普拉斯方程,见式(1)。

(1)

式中:λx、λy、λz分别为x方向、y方向、z方向的导热系数,W/(m·K);qvol为单位体积的生热率,W/m3,非导电部分为0;T为温度,K。

1.1.2 边界条件

1)电解质和铝液层为等温区,其温度会根据外界扰动引起热平衡的变化来自行调节。电解质和铝液与槽帮和槽内衬的传递热量服从牛顿换热公式。

2)切片模型除上部、侧面和底部外均为绝热面,切片模型绝热面之间不会发生热量的传递[23]。

3)槽周围环境温度为定值,取车间实测的环境温度40 ℃。

4)槽体外表面对流热损失Qc的计算公式见式(2)。

Qc=ac(t1-t0)A

(2)

式中:ac为对流换热系数,J/(m2·s·℃);t1为槽外壁温度,℃;t0为环境温度,℃;A为散热面积,m2。

5)槽体外表面辐射热损失Qr的计算公式见式(3)。

Qr=εκφ[(t1+273)4-(t0+273)4]A

(3)

式中:ε为槽壳散热表面的黑度;κ为史蒂芬-玻尔兹曼常数;φ为辐射表面与相邻表面相互辐射角度系数;t1和t0分别为辐射物体壁面温度和周围环境温度,℃;A为辐射物体的辐射表面积,m2。

查找资料得,铝电解槽表面粗糙氧化钢的槽壳,黑度可取0.8,覆盖料黑度可取0.4,铝导杆黑度取0.07.角度系数取1[24]。

电解槽热场计算的边界条件需要进行壁面条件的设置,热对流传热方式设置为热通量模型,热辐射传热方式设置为表面对环境辐射模型,铝导杆顶部端头处设为均匀电流,通过电磁热进行多物理场耦合得到热场分布结果。

1.2 流场数学模型

1.2.2 流体动力学控制方程

铝电解槽中铝液和电解质的湍流多相流运动的雷诺时均Navier-Stocks方程组见式(4)～(5)。

连续性方程

(4)

动量方程

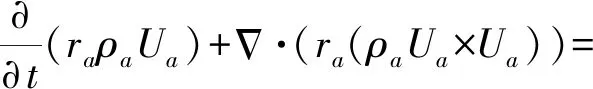
(5)

式中:ra为a相的体积分数,%;ρa为a相的密度,kg/m3;Ua为a相的流速,m/s;Pa为a相的压力,Pa;μaeff为流体的有效黏度,m2/s;SMa为作用于a相的外部体积力,kg·m/s2;Ma为其他流动相对a相的内部表面作用力,kg·m/s2。

铝电解槽内铝液流动为不可压缩湍流流动,当特征尺寸为铝电解槽一半时,雷诺数的量级为105,本文数值模拟铝电解槽流场模型使用k-ε湍流模型确定,见式(6)。

(6)

式中:μaT为湍流黏度,m2/s;κa为a相的湍动能;εa为a相的湍动能耗散速率。

1.2.1 电磁场控制方程

电磁场计算得到的电磁力,是铝电解槽熔体内的电流流经磁场而产生的洛伦磁力,为电场和磁场的耦合结果。根据电流守恒定律和欧姆定律对电场模块电位和电流进行计算,见式(7)～(8)。

(7)

(8)

式中:J为电流密度;φ为标量电位;σi为电导率。

铝电解槽内的磁场问题满足稳态麦克斯韦方程组,见式(9)～(10)。

(9)

B=μH

(10)

1.2.3 边界条件

分析铝电解槽内物质运动方式,无法设置铝电解槽的进、出口边界,只能固定壁面与自由表面边界。根据黏性流动分析,确定边界条件如下:固定壁面处采用无滑移边界条件,即垂直于壁面的速度un和切向速度uτ都为0,即式(11)。

(un)w=(uτ)=0

(11)

并且由于固定壁面上无法湍动,故kw=0,并得式(12)。

(12)

式中:xn表示垂直于固定壁面的方向。

铝电解槽流场分布在多物理场耦合中需要设置2个多物理场耦合,在COMSOL中通过静态电流密度分量关系来耦合电流与磁场,通过洛伦兹力关系来耦合磁场和流场。

2 铝电解槽数值模拟

2.1 热场

2.1.1 切片模型

铝电解槽结构复杂,尺寸较大,根据铝电解槽热传递的特点,将400 kA铝电解槽进行模型简化,得到阳极、阴极左右对称的切片模型,其物理模型如图1所示。

图1 400 kA铝电解槽热场模拟模型

2.1.2 模拟结果

通过热电耦合,得到400 kA铝电解热场切片模拟结果,如图2所示。图2(a)为该厂家400 kA铝电解槽温度分布图,符合铝电解槽运行规律,其中最高温度为978 ℃,电解质温度最高为970.94 ℃。由于在铝电解槽的槽上部、侧部及底部设有热交换,导致边部温度低于中部温度。同时观察得到保温层内温度梯度较大,可以保证良好的保温效果,且保温砖温度在500 ℃以下,可以保证其不易被破坏。图2(b)为该厂家400 kA铝电解槽等温线分布图,从内衬结构温度分布的角度来看,其等温线分布合理,基本沿内衬结构分布,侧部较陡峭,底部较平滑,表明该电解槽炉帮形成状态较好,该电解槽内衬设计较为合理。

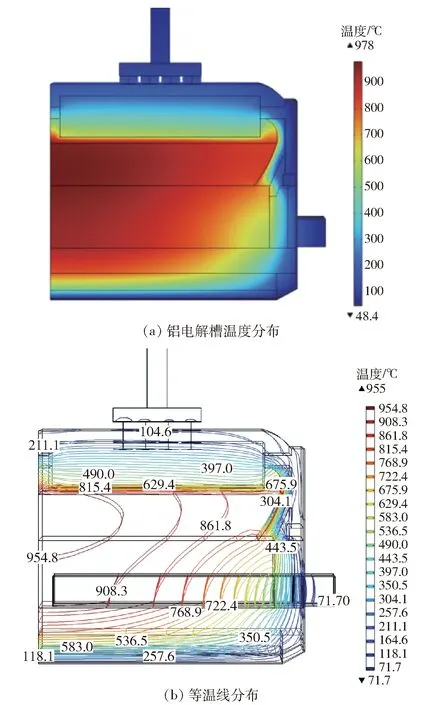
图2 400 kA铝电解热场切片模拟结果

2.2 流场

2.2.1 整槽模型

图3 400 kA铝电解槽流场模拟模型

1)将铝液和电解质的运动考虑为不可压缩黏性牛顿流体。

2)忽略固体颗粒沉降和析出气体浮升作用的影响。

3)忽略熔体内部存在的温度梯度、浓度梯度,将电解质和铝液视为恒温、均质的流体。

4)忽略在生产过程中阳极炭块形状的变化,阳极炭块底面视为平面。

5)忽略熔体中间和底部可能存在的炭渣等固体颗粒物。

6)铝液和电解质的界面视为理想状态,铝液流动视为稳态不可压缩流体。由于密度不同,铝液位于电解槽的下部,2层熔体互不掺杂。

2.2.2 模拟结果

本文在电磁耦合的基础上,通过COMSOL计算得到电解槽铝液层的流场。图4为该厂家400 kA铝电解铝液层流场模拟图,其中图4(a)为铝液层数值模拟结果,图4(b)为x分量方向下铝液速度图,图4(c)为y分量方向下铝液速度图,图4(d)为z分量方向下铝液速度图。图5为该铝电解槽流场数值模拟中电磁力分布图,其中图5(a)为x分量方向下电磁力分布图,图5(b)为y分量方向下电磁力分布图,图5(c)为z分量方向下电磁力分布图。

2002年底，蔡振华担任总局乒羽中心副主任。2005年3月，蔡振华到中央党校学习。当年8月蔡振华被任命为国家体育总局局长助理。2007年4月国务院决定任命蔡振华为国家体育总局副局长。

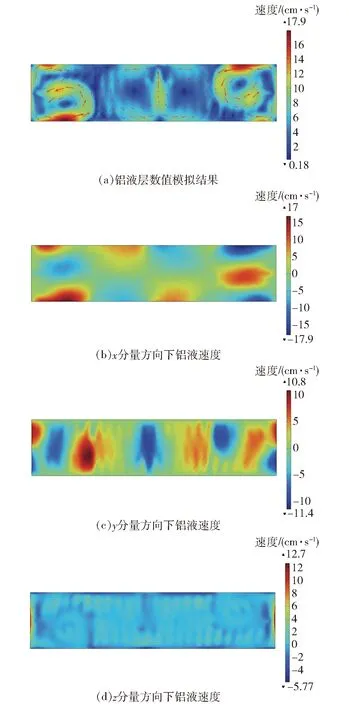
图4 400 kA铝电解铝液层流场模拟

图5 各分量方向下电磁力分布图

图4(a)中数值模拟的铝液层流速平均值为8.18 cm/s,最大值为16.5 cm/s,整体铝液速度分布较均匀。出铝端和烟道端各存在2个较大漩涡和1个较小漩涡,且中间的2个漩涡基本呈中心对称分布,表明该铝电解槽运行较稳定。可以看出,整个电解槽的流场分布大致呈现为4个漩涡形状,从左到右依次为逆时针、逆时针、顺时针和逆时针方向,而铝液层中大涡是由电磁力作用引起的,表明此时电磁力在铝电解槽靠近两端的侧壁面处较大;在电解槽角部还有2个大小不一的小漩涡;最大流速出现在铝电解槽壁面处,可达14 cm/s以上;漩涡中心的流速反而较小。其中,出铝端和烟道端速度约为8～12 cm/s;A面B面中间流速分布较均匀,为5～9 cm/s。

从图4(b)可以看出,x分量方向铝液速度靠近壁面区域流速较大,在出铝端和烟道端的靠近壁面处速度方向相反,中心部分铝液流速较均匀。x分量方向电磁力在出铝端和烟道端偏大,且电磁力方向相反,如图5(a)所示,造成该方向速度场波动。从图4(c)可以看出,y分量方向铝液流动变化波动较大,方向交替分布。y分量方向电磁力在铝电解槽靠近两侧壁面处偏大,且电磁力方向相反,如图5(b)所示,造成该方向速度场波动。从图4(d)可以看出,z分量方向铝液流速整体分布均匀,除出铝端和烟道端小部分流速偏大,其余区域流速分布在0～2 cm/s范围内。z分量方向电磁力在铝电解槽靠近两侧壁面处小部分值偏大,整体图像中电磁力方向变化不大,如图5(c)所示,该方向对速度场影响较小,可以认为z方向上铝液层流场分布均匀稳定。由图4和图5结果综合看出,水平方向上磁场和垂直方向电流作用所产生的电磁力决定了铝液层的流动形态。

3 测试结果

为验证模拟的准确性,对该厂家400 kA铝电解槽分别进行了热场测试和流场测试。

3.1 热场测试结果

对该厂家的一台试验槽进行了能量平衡测试,计算结果与测试结果对比见表1,并在测试结果的基础上对该铝电解槽的散热损失进行了详细的分析,见表2。

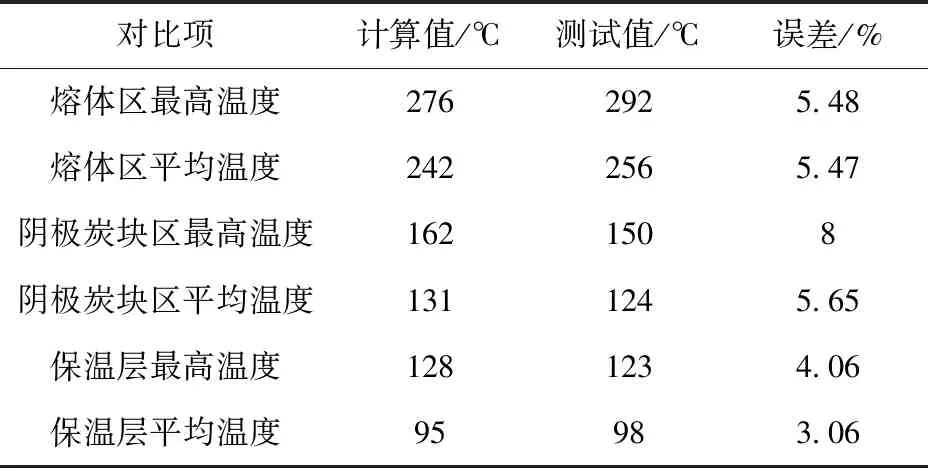
表1 计算结果与测试结果对比表

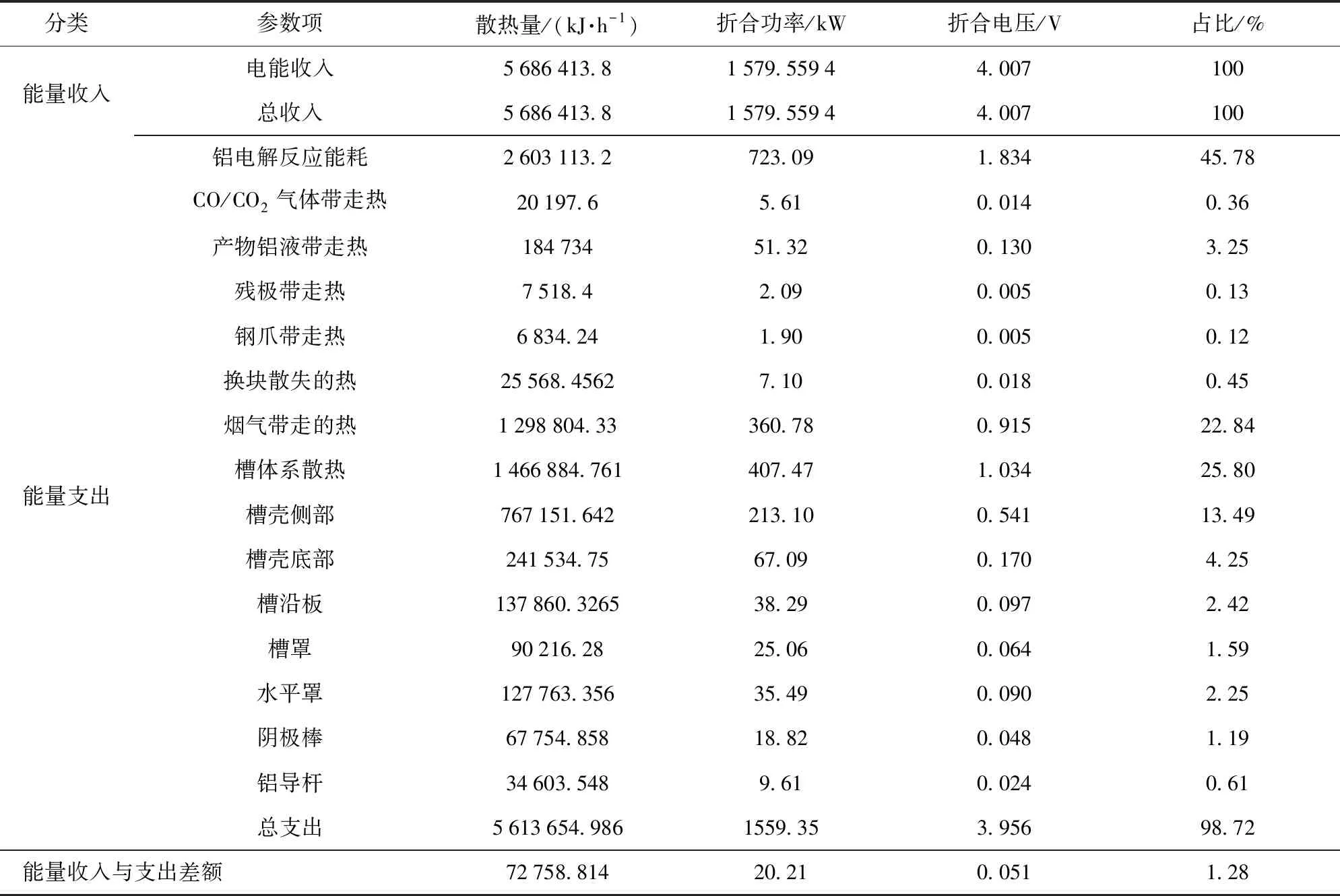
表2 某厂家400 kA铝电解槽测试槽槽体系能量平衡表

从表1可以看出,铝电解槽内热场分布中熔体区、阴极炭块区和保温区的最高温度与平均温度计算值与测试值的误差均不超过10%,表明此次该厂家的400 kA铝电解槽的模拟与测试结果较吻合,证明模拟是有效的,能真实反应铝电解槽热场情况。

散热损失可以衡量整个铝电解槽的能量平衡及能量利用率,从表2看出,该铝电解槽能量平衡测试与计算的误差为1.28%,在误差所允许的范围内。槽总散热损失折合电压为2.122 V,占电解槽能量总收入的52.96%;反应能耗折合电压为1.834 V,占电解槽能量总收入的45.78%,收入和支出占比差距较小,表明该厂铝电解槽收支较为平衡。

利用该模型对铝电解槽的能量平衡进行优化分析,在其侧部和底部增加厚度为10 mm的纳米材料,得到的模拟结果如图6所示。可以看到保温效果明显提高,最高温度为985 ℃,底部保温效果也明显提升。

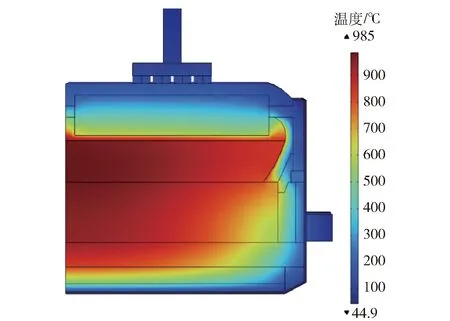
图6 增加10 mm厚纳米材料的铝电解槽温度分布

3.2 流场测试结果

某厂400 kA铝电解槽的铝液流速值如表3所示,铝液的流动图像如图7所示。

表3 某厂家400 kA铝电解槽测点流速表

图7 某厂家400 kA铝电解铝液层流场测试图

结合表3和图7的测点位置及结果可以看出,铝液流速靠近烟道端和出铝端较大,最大值出现在B18、B19、B20、B21、B22、B23、B24这一连续区域,另外B4、B3、B2、B1这一区域流速也较大。全槽平均流速为8.25 cm/s,最大值为17.37 cm/s,全槽流速均匀。从图7可看出,测试铝电解槽有4个漩涡,每个漩涡大小不同。A1～A6和B1～B6构成的漩涡呈逆时针方向流动。A8～A15和B8～B15构成的漩涡呈逆时针方向流动。A17～A20和B17～B21构成的漩涡呈顺时针方向流动,漩涡并不是对称的,B面较宽,A面较窄。A22～A24和B22～B24构成的漩涡呈逆时针方向流动。

测试结果表明,铝液流速方向与模拟结果基本符合,测试得到的速度与模拟结果的速度基本一致。由于模型简化,电磁力场的计算以及在实际生产等影响因素存在一定误差,但是在可接受范围内,即铝液流场计算结果与测试结果基本吻合,模拟是有效的,能真实反应铝液层流场情况。

在上述模拟的基础上,进一步探究不同铝液层高度的铝电解槽对铝液层流速的影响。对铝电解槽进行重新建模,进行电磁力的计算,并将计算结果导入流场模块进行数值模拟,再将得到相应的流场模拟结果进行分析,得到铝液层高度变化与铝液层流速变化的关系,如图8所示。

图8 铝液层高度变化时铝液层流速的变化

从图8可以看出,随着铝液高度的变化,铝液平均流速逐渐增大,从6.108 5 cm/s增加到6.254 7 cm/s;铝液层高度在270～300 mm范围内变化较小,为该槽铝液层高度的合适范围。最大流速总体呈现增大趋势,变化范围大于平均流速的变化范围,从16.4 cm/s增加到16.7 cm/s,表明铝液层高度变化对铝液层最大速度影响较大,铝电解槽的铝液层高度维持在270～280 mm范围内效果较好。

4 结论

1)本文对某厂家400 kA铝电解槽在正常生产条件下的热场和流场进行了数值模拟,模拟结果展现出了400 kA铝电解热场槽切片温度分布图和整槽流场速度分布图。

2)热场模拟结果显示,保温层内温度梯度较大,具有良好的保温效果;等温线分布合理,基本沿内衬结构分布,表明该电解槽炉帮形成状态较好,内衬设计较为合理。流场模拟结果显示,铝液层内速度分布较均匀,有利于铝电解槽稳定运行。

3)本次模拟验证铝电解槽侧部和底部增加厚度10 mm纳米材料,能够提高保温效果;得到铝液层高度维持在270～280 mm范围内效果较好,该结果为铝电解稳定生产提供了科学依据。

感谢上海市Ⅲ类高峰学科—材料科学与工程(高能束智能加工与绿色制造)对本论文的支持。